当前位置： 首页 > news >正文

30个题型+代码(冲刺2023蓝桥杯)

news 2025/7/8 22:21:22

愿意的可以跟我一起刷，每个类型做1~5题 ，4月前还可以回来系统复习 

2月13日 ~ 3月28日，一共32天

一个月时间，0基础省三 --> 省二；基础好点的，省二 --> 省一

目录

🌼前言

🌼一，前缀和

👊（一）3956. 截断数组

🌳Time Limit Exceeded 

🌳Accpted

👊（二）[NewOJ Week 1] 前缀和的因子数

👊（三）P4702 取石子

👊（四）P3056 [USACO12NOV]Clumsy Cows S

🌳栈  AC  12%

🌳栈  AC  75%

🌳栈  AC  100%

🌳前缀和  AC  100%

👊（五）P1147 连续自然数和

🌳AC  56%

🌳AC  100%

🌼二，差分

👊（一）AcWing 3729. 改变数组元素

👊（二）P2367 语文成绩

👊（三）P8772 [蓝桥杯 2022 省 A] 求和

🌼三，二分

👊（一）1460. 我在哪？

🌼四，

🌼五，

🌼六，

🌼七，

🌼八

🌼九，

🌼十，

🌼十一，

🌼十二，

🌼十三，

🌼十四，

🌼十五，

🌼十六，

🌼十七，

🌼十八，

🌼十九，

🌼二十，

🌼二十一，

🌼二十二，

🌼二十三，

🌼二十四，

🌼二十五，

🌼二十六，

🌼二十七，

🌼二十八，

🌼二十九，

🌼三十，

🌼前言

每个类型第一题来自AcWing蓝桥杯集训-每日一题

1，花5块钱

2，上洛谷找替代 / 原题

题型有

前缀和，差分，二分，双指针，递推，递归，并查集，哈希，单调队列，
KMP，Trie，BFS，DFS，拓扑排序，Dijkstra，Floyd，最小生成树，
最近公共祖先，二分图，筛质数，最大公约数，快速幂，组合计数，博弈论，
背包DP，线性DP，区间DP，树型DP，树状数组，线段树，矩阵乘法 

如果你想冲省一，拿22年A组为例，你得拿60分，也就是2道填空题 + 4道编程题

5 + 5 + 10 + 10 + 15 + 15

省赛需要掌握的有：

前缀和，差分，二分，双指针，递归，递推，BFS，DFS，Dijkstra, Floyd，质数筛，最大公约数，背包dp，线性dp，区间dp，组合计数，快速幂，KMP，哈希，并查集，博弈论

围绕省赛需要掌握的类型，针对性地下手

先给大家看个时间复杂度（来源于AcWing）

🌼一，前缀和

👂 多年后再见你 - 乔洋/周林枫 - 单曲 - 网易云音乐

→ 前缀和 & 差分 - OI Wiki (oi-wiki.org)

👊（一）3956. 截断数组

3956. 截断数组 - AcWing题库

类型：枚举，前缀和，中等

还有个坑，虽然10^5 * 10^4 < int，但是由于存在1e5个0的情况，这时答案约等于1e10，就会爆int，所以ans还是开long long 

按着思路枚举，将数组分为3部分，中间部分左边界i游标，右边界j游标

然后在过了所有样例的基础上，再想2组测试，可以就提交

两组测试 

8
7 2 3 2 1 3 10 14
17
3 -2 1 5 -3 4 -2
1

🌳Time Limit Exceeded 

#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int a[100010], n;
bool check(int i, int j) //i左游标, j右游标
{int sum1 = 0, sum2 = 0, sum3 = 0;for(int m = 0; m < n; ++m) {if(m < i)sum1 += a[m];else if(m >= i && m <= j)sum2 += a[m];elsesum3 += a[m];}if(sum1 == sum2 && sum2 == sum3)return true;elsereturn false;
}
int main()
{int i, j;scanf("%d", &n);for(i = 0; i < n; ++i)scanf("%d", &a[i]); //读入数据int ans = 0; //截断方法数量for(i = 1; i < n - 1; ++i) //枚举中间部分for(j = i; j < n - 1; ++j) {if(check(i, j)) ans++;}cout<<ans;return 0;
}

当n = 100000，直接暴力会超时，下面是优化

第一次接触前缀和，本题注意几个点

1，ans开long long

2，三部分都非空

3，数据达到1e5，所以复杂度O(n^2)暴力枚举不行，至少得O(nlogn)

4，代码第17，18行，s[i]表示第一部分前缀和，s[i + 1]表示第二部分前缀和

补充一组测试

8
1 0 1 0 0 0 0 1
10

🌳Accpted

#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int s[100010];
int main()
{int n;scanf("%d", &n);for(int i = 1; i <= n; ++i) { //从1开始读入scanf("%d", &s[i]);s[i] += s[i - 1]; //前缀和, s[i]表示前i项的和}long long cot = 0, ans = 0; //截断方法数量if(s[n] % 3 != 0) cout<<0;else {for(int i = 1; i <= n - 2; ++i) { //整个数组下标从1到nif(s[i] == s[n] / 3) cot++; //if(s[i + 1] == s[n] / 3 * 2) ans += cot; //}cout<<ans;}return 0;
}

解释：cot先自增，ans再加上cot，cot表示第一部分满足三等分的数量，ans表示既满足第一部分三等分，又满足第三部分三等分的情况

👊（二）[NewOJ Week 1] 前缀和的因子数

 P1791 - [NewOJ Week 1] 前缀和的因子数 - New Online Judge (ecustacm.cn)

分类：基础题，欧拉，数论，前缀和 

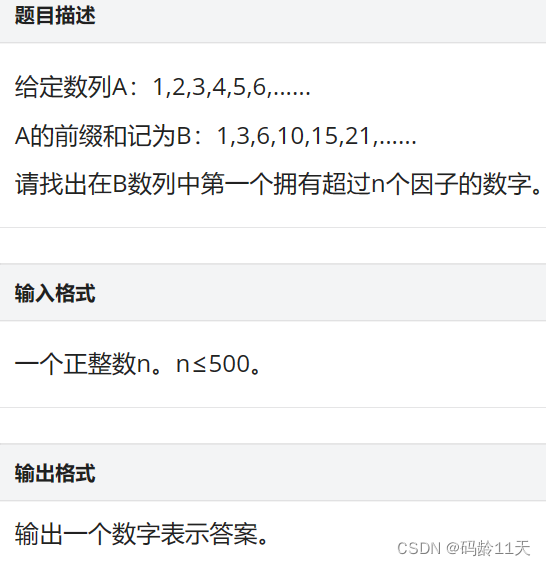
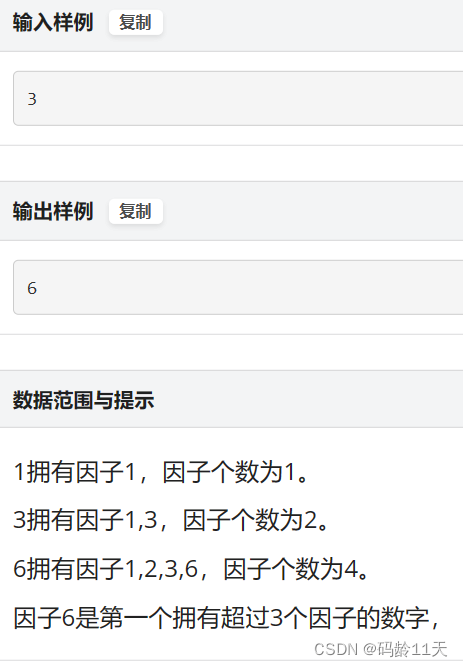
细心是关键

1，前缀和怎么求要会

2，因数怎么求要会

3，i, j游标别搞反了

AC  代码

#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int s[100010];
int main()
{int n;scanf("%d", &n);for(int i = 1;; ++i) {s[i] = i;s[i] += s[i - 1]; //前缀和int sum = 0;for(int j = 1; j * j <= s[i]; ++j) { if(s[i] % j == 0 && j * j != s[i])sum += 2; //求因数else if(s[i] % j == 0 && j * j == s[i])sum++;}if(sum > n) {cout<<s[i];break;}}return 0;
}

👊（三）P4702 取石子

P4702 取石子 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

类型：前缀和，入门

 

一看，感觉好难，为什么才入门。。看了眼题解。。

确实入门，纯前缀和，只是前面加了个类似贪心的判断

→想要分出输赢，石子必须取完

为什么呢？因为“a0视为0”，所以。。显而易见

AC  代码

#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int s[100010];
int main()
{int n;scanf("%d", &n);for(int i = 1; i <= n; ++i) {scanf("%d", &s[i]);s[i] += s[i - 1];}if(s[n] % 2 == 0) cout<<"Bob";else cout<<"Alice";return 0;
}

👊（四）P3056 [USACO12NOV]Clumsy Cows S

P3056 [USACO12NOV]Clumsy Cows S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

大概意思就是，输入偶数长度的括号，最少修改多少次，使左右匹配，也就是都朝里

第一次我用栈做(4条消息) C++ STL 之stack_buyizhu021的博客-CSDN博客_stack赋值

🌳栈  AC  12%

#include<iostream>
#include<stack> //st.push(), st.pop(), st.top()
using namespace std;
string s;
int main()
{stack<char>st;cin>>s;for(int i = 0; i < s.size(); ++i) {if(st.size() == 0)st.push(s[i]); //元素不足2个else if(st.size() >= 1) {if(st.top() == '(' && s[i] == ')') {st.pop(); //如果栈顶元素和新的元素匹配}elsest.push(s[i]); //不匹配就把新的元素入栈}}cout<<st.size();return 0;
}

原来是忘记对结果分类讨论了

如果最后剩下 ))(( 或者 ((((，都需要2次；而剩下 )((( 需要3次

🌳栈  AC  75%

#include<iostream>
#include<stack> //st.push(), st.pop(), st.top()
using namespace std;
string s;
int main()
{stack<char>st;cin>>s;for(int i = 0; i < s.size(); ++i) {if(st.size() == 0)st.push(s[i]); //元素不足2个else if(st.size() >= 1) {if(st.top() == '(' && s[i] == ')') {st.pop(); //如果栈顶元素和新的元素匹配}elsest.push(s[i]); //不匹配就把新的元素入栈}}//分类讨论int a = 0, b = 0;for(int i = 0; i <st.size(); ++i) {if(s[i] == ')') a++;if(s[i] == '(') b++;}int c = min(a, b) + (max(a, b) - min(a, b)) / 2;cout<<c;return 0;
}

找到问题了，第23，24行，应该用st[i]代替s[i]，无奈栈没有这种用法，应该改用st.top(), st.pop()来操作

🌳栈  AC  100%

#include<iostream>
#include<stack> //st.push(), st.pop(), st.top()
using namespace std;
string s;
int main()
{stack<char>st;cin>>s;for(int i = 0; i < s.size(); ++i) {if(st.size() == 0)st.push(s[i]); //元素不足2个else if(st.size() >= 1) {if(st.top() == '(' && s[i] == ')') {st.pop(); //如果栈顶元素和新的元素匹配}elsest.push(s[i]); //不匹配就把新的元素入栈}}//分类讨论int a = 0, b = 0;while(!st.empty()) {if(st.top() == ')') {a++;st.pop();}else if(st.top() == '(') {b++;st.pop();}}int c;if(a % 2 == 1) c = 2 + (a + b - 2) / 2;else c = (a + b) / 2;cout<<c;return 0;
}

常犯错误了，栈就要用栈的表达，不要老想着什么st[i]，日后多多复盘

#include<stack>
int main()
{stack<char>st;st.push();st.top();st.pop();if(!st.empty())......return 0;
}

🌳前缀和  AC  100%

说实话，怎么用前缀和我没想清楚，不过你可以用))((, ((((, ))))三个例子去模拟以下就知道了

#include<iostream>
using namespace std;
string s;
int main()
{cin>>s;int m = 0, n = 0;for(int i = 0; i < s.size(); ++i) {if(s[i] == '(') m++;else m--;if(m == -1) {n++;m = 1;}}cout<<n + m / 2;return 0;
}

👊（五）P1147 连续自然数和

P1147 连续自然数和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：普及-，前缀和，双指针 

 

真的就前缀和 + 双指针

🌳AC  56%

最后三个样例TLE(Time Limit Exceeded)超时了 

想法是，把第8，9行代码去掉，放到第二部分里算前缀和，这样就少一个O(n)的复杂度

毕竟题目是2e6的数据？

#include<iostream>
using namespace std;
int s[10010];
int main()
{int n, i, j;cin>>n;for(i = 1; i <= 10010; ++i)s[i] = i + s[i - 1]; //前缀和for(i = 0, j = 2; i <= n / 2;) {if(s[j] - s[i] == n) {cout<<i + 1<<" "<<j<<endl;i++; //漏了会无限循环}if(s[j] - s[i] > n) //尺取法i++; //左指针if(s[j] - s[i] < n)j++; //右指针}return 0;
}

我们用sum代替前缀和的差值，注意 sum += j 和 sum -= i 与 j++ 和 i++ 的相对位置关系

🌳AC  100%

#include<iostream>
using namespace std;
int s[10010];
int main()
{int n, i, j, sum = 3;cin>>n;for(i = 0, j = 2; i <= n / 2;) {if(sum == n) {cout<<i<<" "<<j<<endl;sum -= i;i++; //漏了会无限循环}if(sum > n) {//尺取法sum -= i;i++; //左指针}if(sum < n) {j++; //右指针sum += j;}}return 0;
}

🌼二，差分

👂  自在的少年 - 要不要买菜 - 单曲 - 网易云音乐

→ 差分算法介绍_木木夕夕山的博客-CSDN博客_差分算法 

→ (1条消息) 算法笔记（六）：差分法_G鸦青的博客-CSDN博客_差分法 

→ 前缀和 & 差分 - OI Wiki (oi-wiki.org)

→ 前缀和、二维前缀和与差分的模板小总结 - AcWing 

概以括之

差分是前缀和的逆运算，假设有两个数组a[], b[]，数组a是数组b的前缀和

即a[i] = b[1] + b[2] + ... + b[i]，那么数组b就是a的差分数组

差分算法有什么用呢，比如给定数组a有n个元素，要求在[left, right]上，每个元素 +c，这时你可能会想，遍历一次，加c不就好了，可是这样时间复杂度达到O(n)，而采用差分只有O(1)的复杂度

如果进行m次区间[left, right] +c 或 -c 的操作呢，这时遍历m次的复杂度为O(nm)，而差分只需O(m)

在数据量达到1e5的情况下，直接遍历会TLE，对于OI赛制只能拿到10%~50%的分，ACM赛制0分

所以学习差分还是有必要的 

具体操作 

给定数组a，n个元素，我们创建数组b，为数组a的差分数组

令b[i] = a[i] - a[i - 1]，因为a是b的前缀和数组 

模板 

#include<iostream>
using namespace std;
int n;
int a[10010], b[10010];
//插入函数
void insert(int l, int r, int c)
{b[l] += c;b[r + 1] -= c;
}
int main()
{cin>>n;//输入数据for(int i = 1; i <= n; ++i)cin>>a[i];//差分后的数组bfor(int i = 1; i <= n; ++i)insert(i, i, a[i]);//执行操作int l, r, c;cin>>l>>r>>c;insert(l, r, c);//输出操作后数组for(int i = 1; i <= n; ++i) {b[i] += b[i - 1]; //前缀和cout<<b[i]<<" ";}return 0;
}

执行m次只需在“执行操作”那里，加个while(m--)，不过我更习惯while(m){ ......m--; }

8
1 2 3 4 5 6 7 8
2 5 3
1 5 6 7 8 6 7 8

先记套路，你可以假设1 3 5 7的数组a，经过insert()函数后，得到的数组b就是1 2 2 2，数组b的前缀和就是原来的数组a 

👊（一）AcWing 3729. 改变数组元素

3729. 改变数组元素 - AcWing题库

标签：中等，差分，区间合并

 

题目没给初始数组，所以我们只需要差分数组b

第二是，我们假定初始长度就为n，用一个for(int i = 1; i <= n; ++i)循环遍历1~n

如果输入的x大于等于当前的长度 i ，就对所有元素执行insert操作

如果输入的x小于 i ，只需要insert(i - x + 1, i)，i 表示最后一个元素

#include<iostream>
#include<cstdio> //scanf(), printf()
#include<cstring> //memset()
using namespace std;
int b[200010]; //题目中没有给定初始数组，所以不需要数组a
void insert(int l, int r)
{b[l] += 1;b[r + 1] -= 1; //套路
}
int main()
{int t, n;scanf("%d", &t);while(t) {scanf("%d", &n);memset(b, 0, sizeof(b)); //初始化//执行操作for(int i = 1; i <= n; ++i) {int x;scanf("%d", &x); //每输入一个数, 就操作一次if(x == 0) continue; //跳过本次else if(x >= i) insert(1, i); //全部操作一次else insert(i + 1 - x, i);}for(int i = 1; i <= n; ++i)b[i] += b[i - 1]; //前缀和得到操作后的数组for(int i = 1; i <= n; ++i) {if(b[i] <= 1) printf("%d ", b[i]);else printf("1 "); //如果大于1就输出1}printf("\n");t--;}return 0;
}

👊（二）P2367 语文成绩

P2367 语文成绩 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：普及/提高-

这是一道最简单模板题，不需要变形，直接套模板就能AC

不开O2优化就AC  80%，开了AC  100%  

能直接套模板的题，基本一次过，而且耗时才几分钟

#include<iostream>
#include<cstdio> //scanf(), printf()
using namespace std;
int a[5000010], b[1000010];
void insert(int l, int r, int c)
{b[l] += c;b[r + 1] -= c; //模板
}
int main()
{int n, p;scanf("%d%d", &n, &p);for(int i = 1; i <= n; ++i)scanf("%d", &a[i]); //初始分数for(int i = 1; i <= n; ++i)insert(i, i, a[i]); //逆前缀和while(p) { //p次操作int l, r, c;scanf("%d%d%d", &l, &r, &c);insert(l, r, c);p--;}for(int i = 1; i <= n; ++i)b[i] += b[i - 1]; //前缀和int Min = 1e9;for(int i = 1; i <= n; ++i)Min = min(Min, b[i]); //找最小值printf("%d", Min);return 0;
}

👊（三）P8772 [蓝桥杯 2022 省 A] 求和

P8772 [蓝桥杯 2022 省 A] 求和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：普及-，前缀和，差分 

虽然标签有差分，但我觉得，它只考了前缀和 

 

temp = 数组a[i]的前缀和，然后用a[i] * temp。暴力的话只能AC  70%

temp = a[1],  sum += a[2] * a[1]

temp = a[1] + a[2],  sum += a[3] * (a[1] + a[2])

temp = a[1] + a[2] + a[3],  sum += a[4] * (a[1] + a[2] + a[3])

......

#include<iostream>
using namespace std;
int a[200010];
int main()
{int n;cin>>n;for(int i = 1; i <= n; ++i)cin>>a[i];long long sum = 0, temp = a[1];for(int i = 2; i <= n; ++i) {sum += temp * a[i];temp += a[i];}cout<<sum;return 0;
}

🌼三，二分

👂 活着 - 郝云 - 单曲 - 网易云音乐

→ 二分算法学习_码龄?天的博客-CSDN博客

→ OI Wiki - OI Wiki (oi-wiki.org) 

模板 

int binary_search(int left, int right, int key) 
{int ret = -1; //未搜索到数据返回-1下标int mid;while(left <= right) {mid = left + ((right - left) >> 1); //避免溢出,用该算法if(key > a[mid]) left = mid + 1;else if(key < a[mid]) right = mid - 1;else { //最后检测相等ret = mid;break;}}return ret; //单一出口
}

要用二分算法，首先判断

1，能不能用， 即是不是一个有序数组，这里的“有序”是广义的有序，也就是一个数组中，某个点左侧或右侧都满足某一条件，而另一侧不满足

2，其次判断，左右边界是什么

👊（一）1460. 我在哪？

1460. 我在哪？ - AcWing题库

标签：简单，二分，哈希

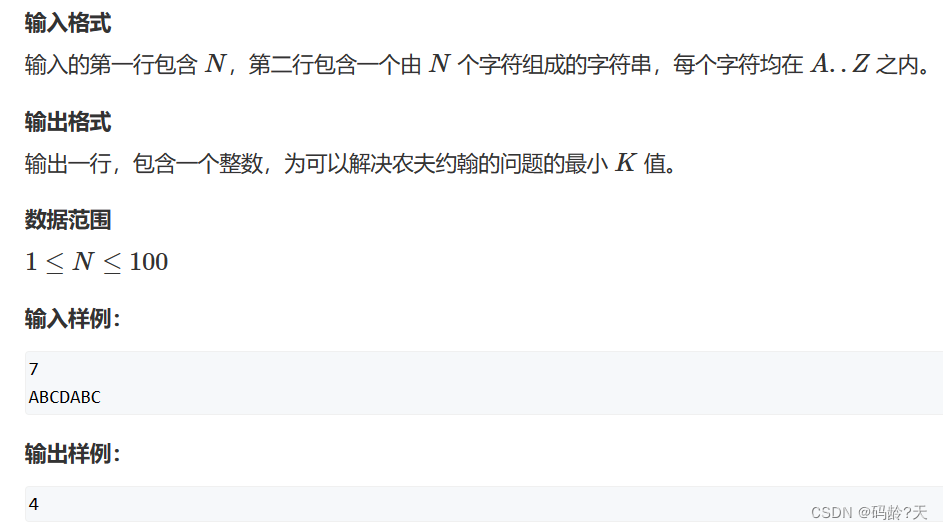
原文是“最小的K值，使任意连续K个，唯一”，比如样例ABCDABC中，有人问为什么CD确定不了2呢，因为任意2个里面，包含AB，而AB的位置显然不是唯一的，3个的话也存在ABC重复，所以只能4个

方法一：二分 + 哈希 ，但是我不会哈希，想了半小时只用二分没结果

方法二：利用set中，元素不重复的特点，但是没想明白怎么做

方法三：考虑到数据量不大，还是暴力 + s.substr()  + s.find()

(9条消息) C++中s.find()和s.rfind()的用法_暖风有凉意的博客-CSDN博客_s.find

1，s.find(str)或s.find(str, pos)要与 != string::npos连用，最后没有找到子串的话，会返回

string::npos 

2，s.substr(i)从下标 i 开始到结尾，s.substr(i, j)从下标 i 开始截取 j 个字符

string s1 = s.substr(j, i);
if(s.find(s1, j + 1) == string::npos)
//没有找到子串, 返回string::nposif(s.find(s1, j + 1) != string::npos)
//找到子串
#include<iostream>
#include<cstring> //s.substr(), s.find()
using namespace std;
int main()
{int n;cin>>n;string s;cin>>s;for(int i = 1; i <= n; ++i) { //i表示截取长度int flag = 1;for(int j = 0; j < n - i; ++j) { //j为截取起始坐标string s1 = s.substr(j, i); //下标j开始截取i个字符if(s.find(s1, j + 1) != string::npos) //j + 1flag = 0;}if(flag) {cout<<i;break;}}return 0;
}

🌼四，

👂 就是我 - 林俊杰 - 单曲 - 网易云音乐 

🌼五，

👂 菲菲 - 沈以诚 - 单曲 - 网易云音乐 

🌼六，

🌼七，

🌼八

🌼九，

🌼十，

🌼十一，

🌼十二，

🌼十三，

🌼十四，

🌼十五，

🌼十六，

🌼十七，

🌼十八，

🌼十九，

🌼二十，

🌼二十一，

🌼二十二，

🌼二十三，

🌼二十四，

🌼二十五，

🌼二十六，

🌼二十七，

🌼二十八，

🌼二十九，

🌼三十，

http://www.lryc.cn/news/7365.html

相关文章：

  • 快速且有效减小代码包的方法
  • 基于matlab评估星载合成孔径雷达性能
  • Linux_基本指令
  • Keras深度学习实战——使用深度Q学习进行SpaceInvaders游戏
  • 从事架构师岗位快2年了，聊一聊我对架构的一些感受和看法
  • 零基础机器学习做游戏辅助第十二课--原神自动钓鱼（二）
  • MapReduce paper(2004)-阅读笔记
  • 【蒸滴C】C语言指针入门很难？看这一篇就够了
  • C++11新的类功能
  • Laravel创建定时任务
  • SaveInstanceState
  • Fluent Python 笔记 第 16 章 协程
  • 山东科技大学校历 代码分析 获得以前学期学年的老版校历
  • 第五章.与学习相关技巧—权重初始值(随机初始值，Xavier初始值，He初始值)
  • Linux进程间通信（管道）
  • 写一个基于node.js的api后台管理系统(三)
  • 【23种设计模式】行为型模式详细介绍（上）
  • PID控制算法进阶
  • 嵌入式工程师有什么值得一看的网站和书籍吗？
  • 操作系统的四个特征
  • Django框架之模型shell工具和查看MySQL数据库日志
  • 电脑录屏怎样不录到外界声音？调整这一个开关，即可实现
  • 无需登录复制网站文字的解决方案
  • ccc-Tips for Deep Learning-李宏毅(8)
  • ArkUI新能力，助力应用开发更便捷
  • vue面试题大全
  • P1307 [NOIP2011 普及组] 数字反转
  • 【服务器数据恢复】NetApp存储无法访问的数据恢复案例
  • （考研湖科大教书匠计算机网络）第四章网络层-第三节2：分类编址的IPv4地址
  • Allegro移动器件时附带的孔和线被同步更改的原因和解决办法