GAN和CycleGAN
文章目录
- 1. GAN 《Generative Adversarial Nets》
- 1.1 相关概念
- 1.2 公式理解
- 1.3 图片理解
- 1.4 熵、交叉熵、KL散度、JS散度
- 1.5 其他相关(正在补充!)
- 2. Cycle GAN 《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》
- 2.1 基础理论和推到
- 2.2 实验结果
- 2.3 限制和讨论
本BLOG是个人文章阅读和知识积累,有很多的相关基础知识介绍,小白可放心食用。但由于都是手打的,如果存在问题请联系修改,有的地方博主可能也会有疑问,标出的地方有懂的大佬可留言讨论。当前整理了GAN和CycleGAN的相关内容,接下来还会整理WGAN等内容。
1. GAN 《Generative Adversarial Nets》
Ian J. Goodfellow, Jean Pouget-Abadie, Yoshua Benjio etc.
https://dl.acm.org/doi/10.5555/2969033.2969125
1.1 相关概念
生成模型:学习得到联合概率分布P(x,y)P(x,y)P(x,y),即特征x和标签y同时出现的概率,然后可以求条件概率分布和其他概率分布。学习到的是数据生成的机制。
判别模型: 学习得到条件概率分布P(y∣x)P(y|x)P(y∣x),即在特征x出现的情况下标记y出现的概率
学习一个分布和近似一个分布?
1.2 公式理解
GAN的损失函数:
minGmaxDV(D,G)=Ex∼Pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))](1.1)\underset{G}{min}\underset{D}{max}V(D,G) = E_{x \sim P_{data}(x)}[log D(x)]+E_{z\sim p_{z}(z)}[log(1-D(G(z)))] \tag{1.1}GminDmaxV(D,G)=Ex∼Pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))](1.1)
为了学习数据x的分布pgp_gpg,定义了一个含有噪声的变量分布pz(z)p_z(z)pz(z);V是评分方程(这个值是越大越好的),G是一个生成器,D是一个判别器;训练D最大化真实数据和生成数据的区别,训练G最小化真实数据和生成数据的区别;
注意这个公式有两项,第一项是指是否能正确识别真实的数据;第二项是指是否能够识别生成的数据;
(1) 完美D
- 当D(x)D(x)D(x)完美识别真实数据和生成数据,Ex∼Pdata(x)[logD(x)]E_{x\sim P_{data}(x)}[log D(x)]Ex∼Pdata(x)[logD(x)]趋近于1,而Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]趋近于0,整体趋近于1.
- 当DDD不完美的时候,由于存在logloglog会使得两项都是一个负数;那训练的目的就是使得这个负数尽量小
- 因此需要最大化判别器带来的值,来使得判别器D最佳。
(2) 完美G
- G只和Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]相关,如果G完美忽悠D的时候,Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]输出的结果就是负无穷;
- 当不是那么完美的时候,输出的值就是一个负数;我们目的是使得这个输出尽量小,以使得生成器最佳。
- 所以需要最小化生成器带来值Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]
训练过程
训练D说明
生成器生成的数据就是V(G,D)的第二项的输入:g(z)=xg(z) = xg(z)=x,那么对z的求和就可以变为对x的求和。
将V(G,D)V(G,D)V(G,D)展开成积分/求和的形式
V(G,D)=∫xpdata⋅log(D(x))dx+∫zpz(z)⋅log(1−D(g(z)))=∫xpdata⋅log(D(x))+pg(x)⋅log(1−D(x))dx(1.2)\begin{aligned} V(G,D) &= \int_x p_{data} \cdot log(D(x))dx + \int_z p_z(z) \cdot log(1-D(g(z))) \\ &=\int_x p_{data} \cdot log(D(x)) + p_g(x) \cdot log(1-D(x))dx \end{aligned} \tag{1.2} V(G,D)=∫xpdata⋅log(D(x))dx+∫zpz(z)⋅log(1−D(g(z)))=∫xpdata⋅log(D(x))+pg(x)⋅log(1−D(x))dx(1.2)
对于 任意的(a,b)∈R2\{0,0}(a,b) \in R^2 \backslash \{0,0\}(a,b)∈R2\{0,0},函数y→alog(y)+blog(1−y)y \rightarrow a log(y) + blog(1-y)y→alog(y)+blog(1−y)是一个凸函数,我们需要求这个函数的最大值,就求导数
ay+b1−y=0y=aa+b\begin{aligned} \frac{a}{y}+\frac{b}{1-y} = 0 \\ y = \frac{a}{a+b} \end{aligned} ya+1−yb=0y=a+ba
则在y=aa+by = \frac{a}{a+b}y=a+ba的时候有最大值,对应于判别器的概率即为:
DG∗(x)=pdata(x)pdata(x)+pg(x)D_G^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}DG∗(x)=pdata(x)+pg(x)pdata(x)
将最优解带入到价值函数之中
C(G)=maxDV(G,D)=Ex∼pdata[logDG∗(x)]+Ez∼pz[log(1−DG∗(G(z)))]=Ex∼pdata[logpdata(x)pdata(x)+pg(x)]+Ex∼pg[logpg(x)pdata(x)+pg(x)](1.3)\begin{aligned} C(G) &= \underset{D}{max}V(G,D) \\ &= E_{x \sim p_{data}}[log D_G^*(x)] + E_{z \sim p_z}[log(1-D_G^*(G(z)))] \\ &= E_{x \sim p_{data}}[log \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}] + E_{x \sim p_g}[log \frac{p_g(x)}{p_{data}(x) + p_g(x)}] \end{aligned} \tag{1.3} C(G)=DmaxV(G,D)=Ex∼pdata[logDG∗(x)]+Ez∼pz[log(1−DG∗(G(z)))]=Ex∼pdata[logpdata(x)+pg(x)pdata(x)]+Ex∼pg[logpdata(x)+pg(x)pg(x)](1.3)
根据KL散度和JS散度的定义,可以将上面的公式改写为
C(G)=KL(Pdata∣∣pdata+pg2)+KL(pg∣∣pdata+pg2)−log(4)=2⋅JSD(pdata∣∣pg)−log(4)(1.4)\begin{aligned} C(G) &= KL(P_{data} || \frac{p_{data}+p_g}{2}) + KL(p_g || \frac{p_{data}+p_g}{2}) -log(4) \\ &= 2 \cdot JSD(p_{data}||p_g) - log(4) \end{aligned} \tag{1.4} C(G)=KL(Pdata∣∣2pdata+pg)+KL(pg∣∣2pdata+pg)−log(4)=2⋅JSD(pdata∣∣pg)−log(4)(1.4)
注意pdata+pg2\frac{p_{data}+p_g}{2}2pdata+pg这里除以2是为了保证是一个分布(即概率的积分是等于1的)
在固定D训练G的时候,我们就是为了最小化这个C(G)C(G)C(G),根据上面推导:
所以给出结论:当pg=pdp_g = p_dpg=pd时,DG∗(x)=12D_G^*(x) = \frac{1}{2}DG∗(x)=21,因此C(G)=log12+12=−log4C(G) = log\frac{1}{2} + \frac{1}{2} = -log4C(G)=log21+21=−log4,可以得到最小的C(G)C(G)C(G)
1.3 图片理解
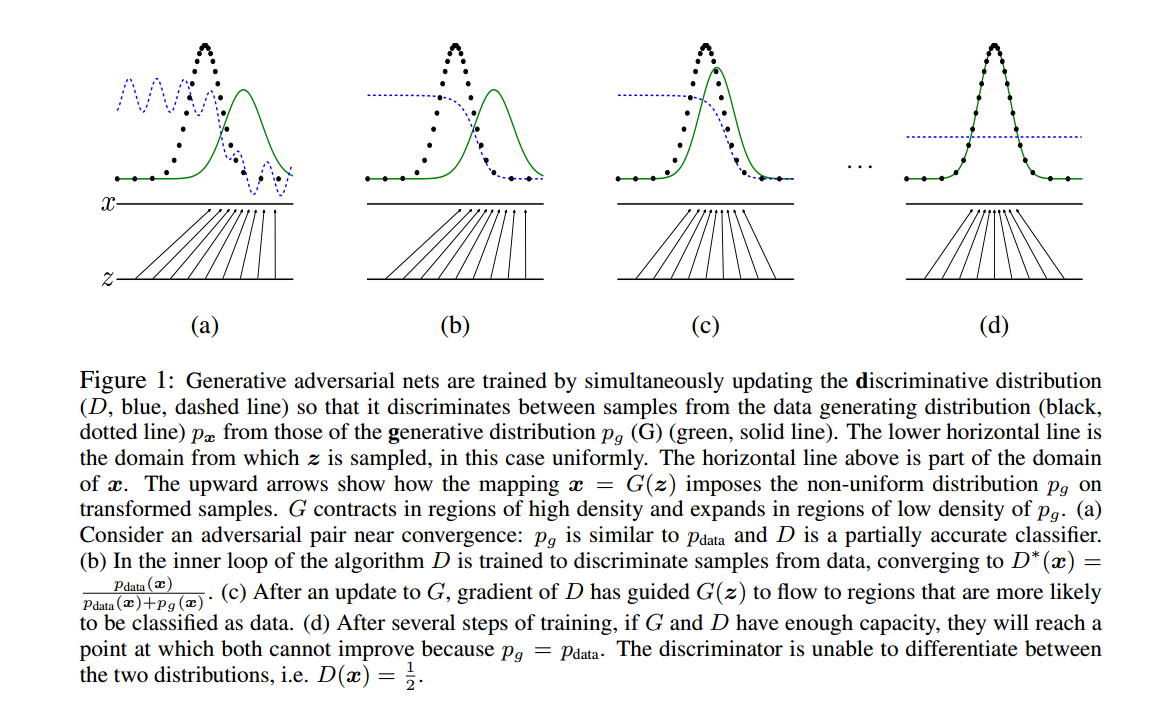
绿色是生成的分布;黑色是真实分布;蓝色是判别器的分布
(b)表示训练辨别器,使得辨别器可以非常好地区分二者
©表示训练生成器,继续欺骗判别器
1.4 熵、交叉熵、KL散度、JS散度
熵(Entropy)
K-L散度源于信息论,常用的信息度量单位为熵(Entropy)
H=−∑i=1Np(xi)⋅logp(xi)H = -\sum_{i=1}^{N}p(x_i) \cdot logp(x_i)H=−i=1∑Np(xi)⋅logp(xi)
注意这个对数没有确定的底数(可以使2、e或者10)。
熵度量了数据的信息量,可以帮助我们了解用概率分布近似代替原始分布的时候我们到底损失了多少信息;但问题是如何将熵值压缩到最小值,即如何编码可以达到最小的熵(存储空间最优化)。
-
交叉熵: 量化两个概率分布之间的差异
H(p,q)=−∑xp(x)logq(x)H(p,q) = -\sum_{x}p(x) \; log \; q(x)H(p,q)=−x∑p(x)logq(x) -
KL散度(kullback-Leibler divergence):量化两种概率分布 P和Q之间差异的方式,又成为相对熵
将熵的定义公式稍加修改就可以得到K-L散度的定义公式:
DKL(P∣∣Q)=∑i=1Np(xi)⋅(logp(xi)−logq(xi))=∑i=1Np(xi)⋅logp(xi)q(xi)D_{KL}(P||Q) = \sum_{i=1}^{N} p(x_i) \cdot (log p(x_i) - log q(x_i)) = \sum_{i=1}^{N}p(x_i) \cdot log \frac{p(x_i)}{q(x_i)}DKL(P∣∣Q)=i=1∑Np(xi)⋅(logp(xi)−logq(xi))=i=1∑Np(xi)⋅logq(xi)p(xi)
其中ppp和qqq分别表示数据的原始分布和近似的概率分布。
根据公式所示,K-L散度其实是数据的原始分布p和近似分布之间的对数差的期望。如果用2位底数计算,K-L散度表示信息损失的二进制位数,下面用期望表示式展示:
DKL(P∣∣Q)=E[logp(x)−q(x)]D_{KL}(P||Q) = E[log p(x) - q(x)]DKL(P∣∣Q)=E[logp(x)−q(x)]
注意:
- 从散度的定义公式中可以看出其不符合对称性(距离度量应该满足对称性)
- KL散度非负性
JS散度(Jensen-shannon divergence)
由于K-L散度是非对称的,所以对其进行修改,使得其能够对称,称之为 JS散度
(1) 设 M=12(P+Q)M = \frac{1}{2}(P+Q)M=21(P+Q),则:
DJS(P∣∣Q)=12DKL(P∣∣M)+12DKL(Q∣∣M)D_{JS}(P||Q) = \frac{1}{2}D_{KL}(P||M) + \frac{1}{2}D_{KL}(Q||M)DJS(P∣∣Q)=21DKL(P∣∣M)+21DKL(Q∣∣M)
(2) 将KL散度公式带入上面
DJS=12∑i=1Np(xi)log(p(xi)p(xi)+q(xi)2)+12∑i=1Nq(xi)⋅log(q(xi)p(xi)+q(xi)2)D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{p(x_i)}{\frac{p(x_i) + q(x_i)}{2}}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{q(x_i)}{\frac{p(x_i)+q(x_i)}{2}})DJS=21i=1∑Np(xi)log(2p(xi)+q(xi)p(xi))+21i=1∑Nq(xi)⋅log(2p(xi)+q(xi)q(xi))
(3) 将logloglog中的12\frac{1}{2}21放到分子上
DJS=12∑i=1Np(xi)log(2p(xi)p(xi)+q(xi))+12∑i=1Nq(xi)⋅log(2q(xi)p(xi)+q(xi))D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{2p(x_i)}{p(x_i) + q(x_i)}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{2q(x_i)}{p(x_i)+q(x_i)})DJS=21i=1∑Np(xi)log(p(xi)+q(xi)2p(xi))+21i=1∑Nq(xi)⋅log(p(xi)+q(xi)2q(xi))
(4) 提出2
DJS=12∑i=1Np(xi)log(p(xi)p(xi)+q(xi))+12∑i=1Nq(xi)⋅log(q(xi)p(xi)+q(xi))+log(2)D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{p(x_i)}{p(x_i) + q(x_i)}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{q(x_i)}{p(x_i)+q(x_i)}) + log(2)DJS=21i=1∑Np(xi)log(p(xi)+q(xi)p(xi))+21i=1∑Nq(xi)⋅log(p(xi)+q(xi)q(xi))+log(2)
注意这里是因为∑p(x)=∑q(x)=1\sum p(x) = \sum q(x) = 1∑p(x)=∑q(x)=1
JS散度的缺陷:当两个分布完全不重叠的时候,几遍两个分布的中心离得很近,其JS散度都是一个常数,所以其获取的梯度是0,是没有办法进行更新的。而两个分布没有重叠的原因:从理论和经验而言,真实的数据分布其实是一个低维流形(不具备高维特征),而是存在一个嵌入在高维度的低维空间内。由于维度存在差异,数据很可能不存在分布的重合。
1.5 其他相关(正在补充!)
2. Cycle GAN 《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》
一开始是应用到图像风格迁移上面的

2.1 基础理论和推到
- 概念描述
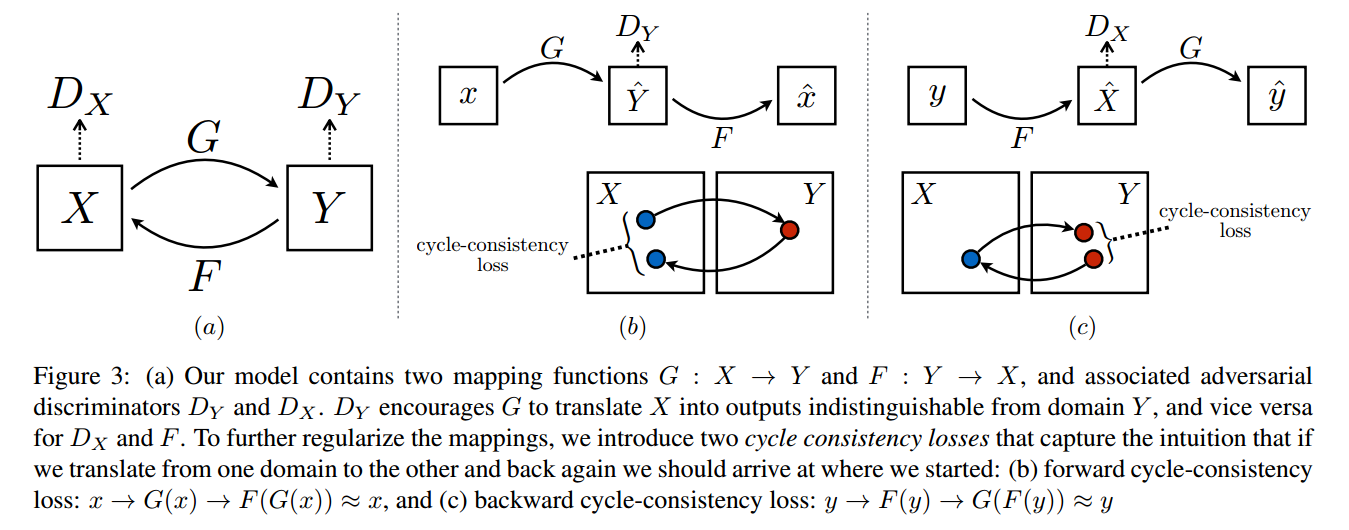
CycleGAN具有一个双判别器结构
- G:从X到Y的生成器
- F:从Y到X的生成器
- DxD_xDx:判别生成的X是真实X,还是生成的X
- DyD_yDy:判别生成的Y是真实Y,还是生成的Y
训练过程
- forward cycle-consistency loss
x→G(x)→F(G(x))≈xx \rightarrow G(x) \rightarrow F(G(x)) \approx xx→G(x)→F(G(x))≈x- 输入xxx,生成器GGG,得到输出y^=G(x)\hat{y} = G(x)y^=G(x),判别器DyD_yDy判别该输出是真实yyy还是生成的;
- 将y^\hat{y}y^继续输入到另一个生成器FFF之中,输出x^=F(y^)=F(G(x))\hat{x} = F(\hat{y}) = F(G(x))x^=F(y^)=F(G(x))
- backward cycle-consistency loss
y→F(y)→G(F(y))≈yy \rightarrow F(y) \rightarrow G(F(y)) \approx yy→F(y)→G(F(y))≈y- 输入yyy,生成器FFF,得到输出x^=F(y)\hat{x} = F(y)x^=F(y),判别器DxD_xDx判断该输出是真实xxx还是生成的;
- 将x^\hat{x}x^继续输入到另一个生成器GGG之中,输出y^=G(x^)=G(F(y))\hat{y} = G(\hat{x}) =G(F(y))y^=G(x^)=G(F(y))
损失函数
L(G,F,Dx,Dy)=LGAN(G,Dy,X,Y)+LGAN(F,Dx,Y,X)+λLcyc(G,F),(2.1)L(G,F,D_x,D_y) = L_{GAN}(G,D_y,X,Y) + L_{GAN}(F,D_x,Y,X) + \lambda L_{cyc}(G,F), \tag{2.1}L(G,F,Dx,Dy)=LGAN(G,Dy,X,Y)+LGAN(F,Dx,Y,X)+λLcyc(G,F),(2.1)
其中包含有两个原始GAN的损失和一个CycleGAN的损失。
G:X→YG:X \rightarrow YG:X→Y
LGAN(G,Dy,X,Y)=Ey∼pdata(y)[logDy(y)]+Ex∼pdata(x)[log(1−Dy(G(x)))],(2.2)L_{GAN}(G,D_y,X,Y) = E_{y \sim p_{data}(y)}[log D_y(y)] + E_{x \sim p_{data}(x)}[log(1 - D_y(G(x)))], \tag{2.2}LGAN(G,Dy,X,Y)=Ey∼pdata(y)[logDy(y)]+Ex∼pdata(x)[log(1−Dy(G(x)))],(2.2)
F:Y→XF:Y \rightarrow XF:Y→X
LGAN(F,Dy,X,Y)=Ex∼pdata(x)[logDx(x)]+Ey∼pdata(y)[log(1−Dx(F(y)))],(2.3)L_{GAN}(F,D_y,X,Y) = E_{x \sim p_{data}(x)}[log D_x(x)] + E_{y \sim p_{data}(y)}[log(1 - D_x(F(y)))], \tag{2.3}LGAN(F,Dy,X,Y)=Ex∼pdata(x)[logDx(x)]+Ey∼pdata(y)[log(1−Dx(F(y)))],(2.3)
在理论上,对抗学习可以学习到一种映射关系,以生成器G为例,它得到的输出的分布是与目标域是同分布。但是呢,在足够大的生成能力下,一个网络模型可以映射相同一系列输入图像到任意随机排列在目标域的图像中,其中任何一个学到的映射都可以得到与目标域匹配的输出分布。什么意思呢?就是可能有两个不同的生成器生成的图像都可能得到相同的能与目标域匹配的图像分布。为了得到一个满意的输出,因此单单一个对抗损失远远不够。为了进一步减少可能映射函数的空间域,作者认为学习到的映射因该具有循环一致性损失,就如我在方法中说的那样。
Lcyc(G,F)=Ex∼pdata(x)[∣∣F(G(x))−x∣∣1]+Ey∼pdata(y)[∣∣G(F(y))−y∣∣1].(2.4)L_{cyc}(G,F) = E_{x \sim p_{data}(x)}[||F(G(x)) -x||_1] + E_{y \sim p_{data}(y)}[||G(F(y)) - y||_1]. \tag{2.4}Lcyc(G,F)=Ex∼pdata(x)[∣∣F(G(x))−x∣∣1]+Ey∼pdata(y)[∣∣G(F(y))−y∣∣1].(2.4)
2.2 实验结果



2.3 限制和讨论
- 限制:
- 并非所有的例子都是非常好的效果的
- 颜色风格的变化容易实现,但是几何风格的变化难以实现
- 训练数据的特征分布会影响训练的过程,容易导致训练失败(比如只是用马和斑马进行训练,如果加入人骑在马上面进行风格迁移就会失败,因为没有学习到这个特征)
- 成对训练数据和非成对数据训练的效果仍然存在较大的区别
