常见分布函数。
一维常见分布函数
1.离散型
① 0 - 1分布 记 X~B(1,p)
如果X的概率分布为 ( 1 0 p 1 − p ) \begin{pmatrix} 1 & 0 \\ p & 1-p \end{pmatrix} (1p01−p),则称X服从参数为P的0-1分布(0<p<1)。
注:0-1分布又称一次伯努利试验或两点分布。
②二项分布 记 X~B(n,p)
如果X的概率分布为 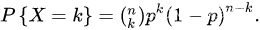 (k=0,1,2,3…n;0<p<1),称X服从参数为(n,p)的二项式分布,又叫N重伯努利试验。
(k=0,1,2,3…n;0<p<1),称X服从参数为(n,p)的二项式分布,又叫N重伯努利试验。
③泊松分布 记 X~P(λ)
如果X的概率分布服从为: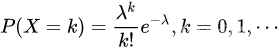 (λ>0).
(λ>0).
则称X服从参数为λ的泊松分布。
表示k个质点来流发生的概率,如某商场8点源源不断往返k人发生的概率。
注:λ是强度,如单位时间内平均来了多少人。
④几何分布 记 X ~ G ( p)
如果X的概率分布为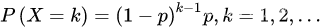
则称X服从参数为p的几何分布。又叫离散型概率分布,无穷伯努利试验。
注1:X表示伯努利试验中事件A首次发生所需要做的试验次数,首中即停止。
注2:几何分布与几何没关系,历史上叫错了。
⑤超几何分布 记 X ~ H(n,N,M)
如果X的概率分布为: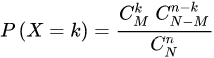 (max{0,n-N+M}<= k <= min{M,n} ; M,N,n为正整数 且 M <= N,n <= N,k为整数).
(max{0,n-N+M}<= k <= min{M,n} ; M,N,n为正整数 且 M <= N,n <= N,k为整数).
2.连续型
①均匀分布 记 X ~ U(a,b)
如果随机变量X的概率密度和分布函数为:
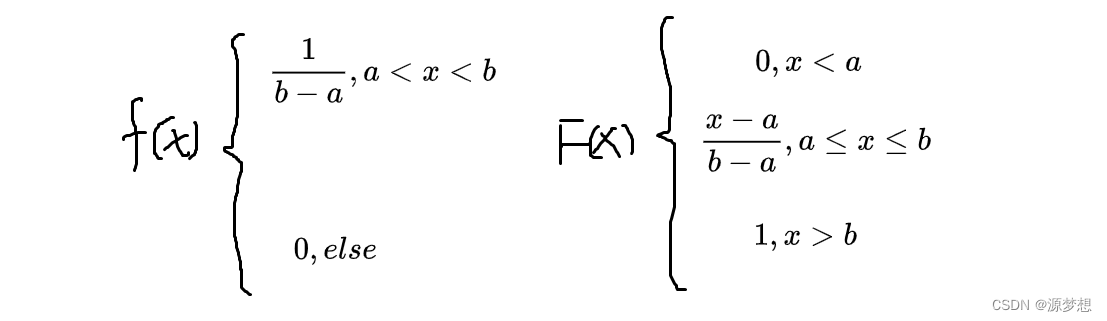
则称X在区间(a,b)上服从均匀分布。
②指数分布 记 X ~ E(λ)
如果随机变量X的概率密度和分布函数为:λ>0
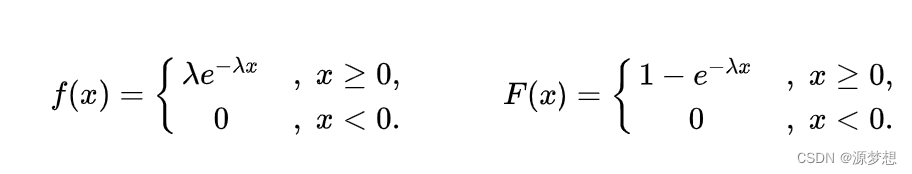
注:这里λ表示失效率。
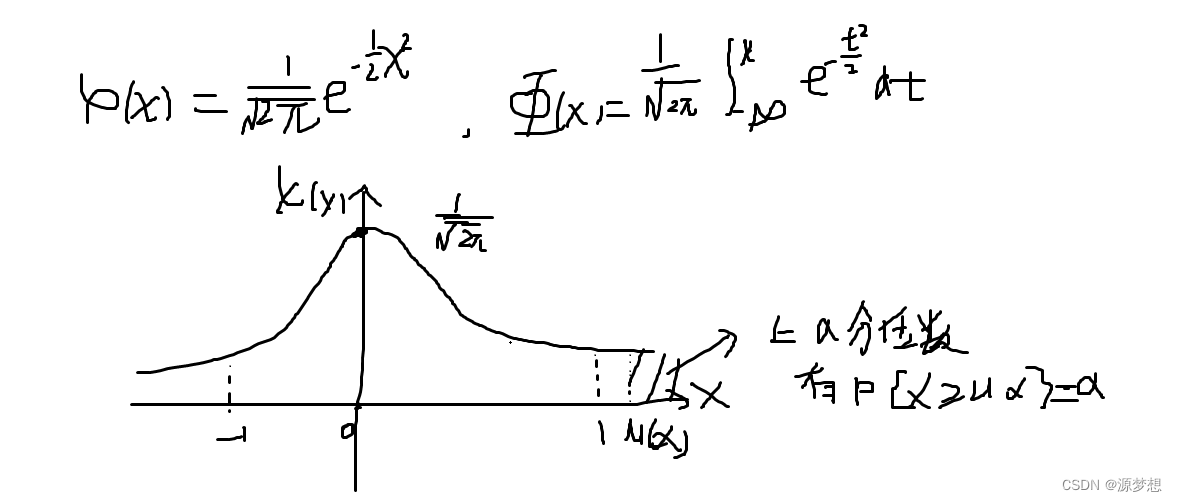
③正态分布 记 X~N(μ,σ2)
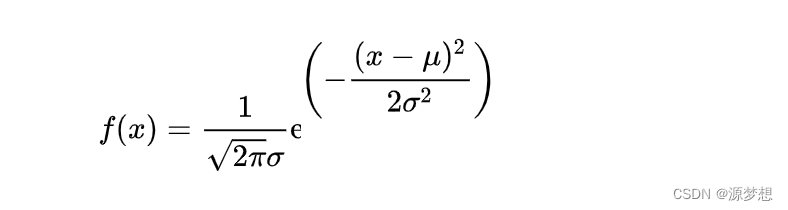
其中 -∞ < μ < +∞, σ > 0, 则称X服从参数为(μ,σ2) 的正态分布或称X为正态变量。
注1:此时f(x)图形关于x = μ 对称,即 f(μ - x) = f(μ + x),并在 x = μ有唯一最大值f(μ)。
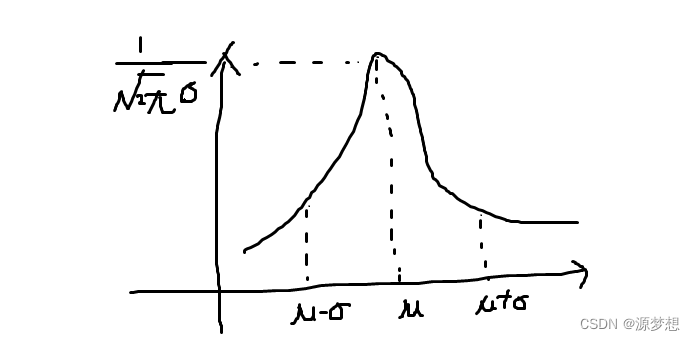
注2:称μ = 0,σ = 1时的正态分布为标准正态分布,通常记为符号φ(x)。其中φ(x)为偶函数,有φ(0) = 1/2,φ(-x) = 1 - φ(x)。
二维常见分布函数
1.连续型
①二维均匀分布
称(X,Y)在平面有界区域D上服从均匀分布,如果(X,Y)的概率密度为:
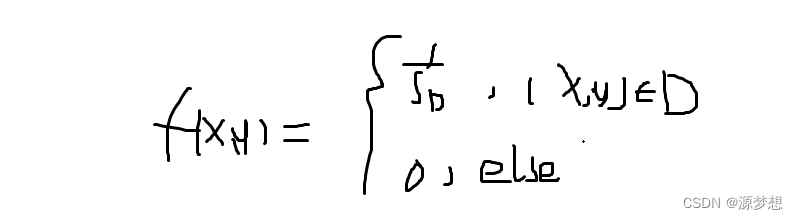
注:将密度均匀撒在区域D上.sD为D面积。
②二维正态分布 记 (X,Y)~(μ1,μ2,σ12,σ22,ρ)
如果(X,Y)的密度函数为: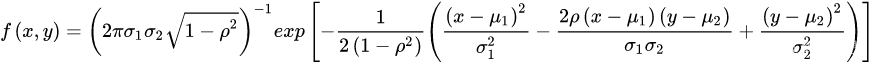
其中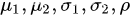 都是常数我们称(X,Y)服从参数为
都是常数我们称(X,Y)服从参数为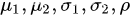 的二维正态分布.
的二维正态分布.
注:ρ为XY的线性相关系数。
