离散数学 | 图论 | 欧拉图 | 哈密顿图 | 割点 | 桥(欧拉图和哈密顿图有没有割点和桥?)
本文主要解决以下几个问题:
1.欧拉图能不能有割点,能不能有桥?
2.哈密顿图能不能有割点,能不能有桥?
首先我们要明白几个定义
割点的定义就是在一个图G中,它本来是连通的,去掉一个点v以后这个图G就不连通了,那么点v就被叫做割点。
桥的定义就是在一个图G中,它本来也是连通的,去掉一条边x以后这个图就不连通了,那么边x就被称为桥。
欧拉图是拥有欧拉闭迹的图。
所谓欧拉闭迹,包含两层概念:“闭”和“迹”。
我们先来说什么是迹,所谓“迹”,就是用一笔可以从一个顶点出发,一直沿着边走,走到另一个顶点停止。在走的过程中,可以有重复的点,但是不能有重复的边。也就是说一个点可以经过两次以上,但是一个边只能走一次。
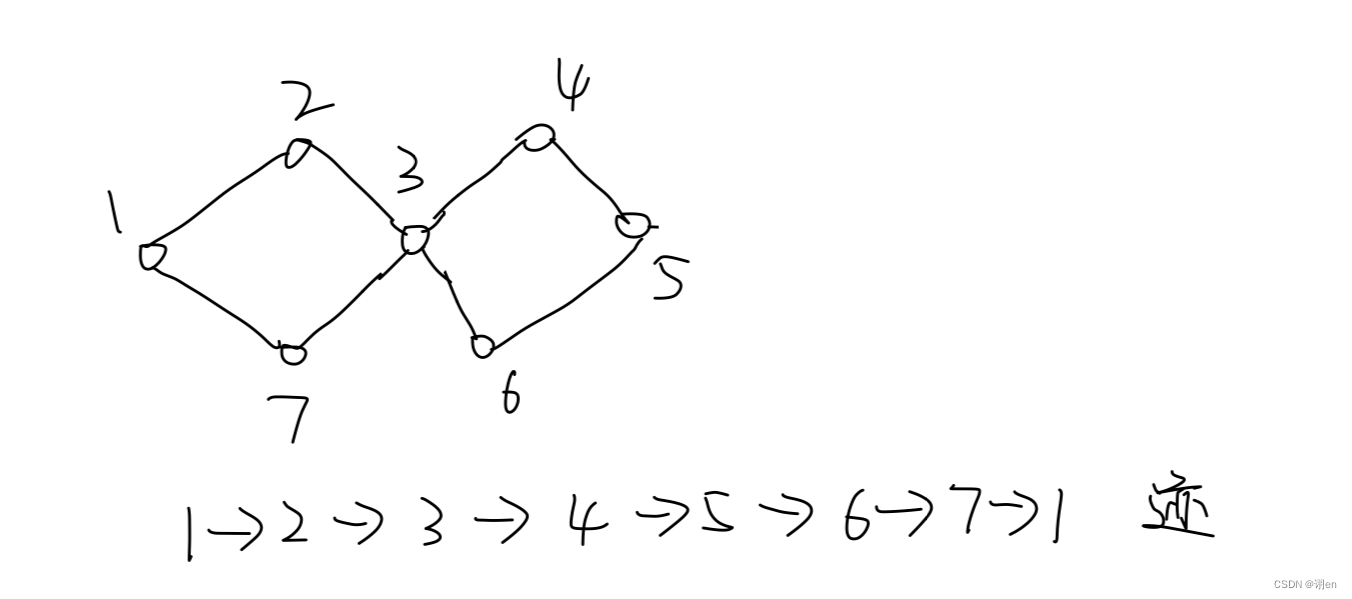
如图:从1走到5,最后再回到1,这就是一条迹。
我们再来说什么是“闭”,所谓闭,就是闭合的意思,也就是说这条迹最后要回到起点,形成一条闭合回路。上图所示的迹也是一条闭迹。
我们可以看到上面画的这个图拥有一套欧拉闭迹,那么他就是一个欧拉图。
如果这个图去掉点3,他就变成不连通的了,那么点3就是一个割点,显然欧拉图是可以有割点的,有割点的图也可以是欧拉图。
那么欧拉图能不能有桥呢?
我们先来试着想一想,欧拉图必须要从一个点出发走回去,边不能重复。那么如果有桥的话,对于两个划分以后的子图,我们为了从一个顶点出发,最后再回到这个顶点,不得不从这个桥走两遍,这显然违背了欧拉图的定义。
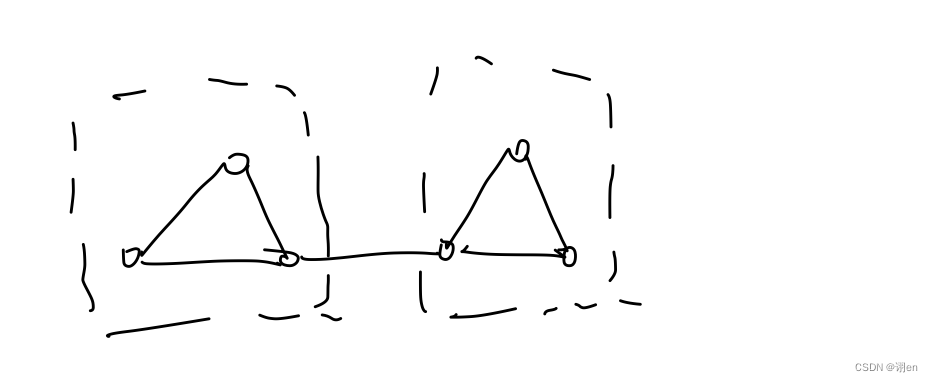
如果需要严谨证明的话,我们可以先由欧拉图得到,在图上任意去掉一条边x,图依然是连通的。如果去掉桥的话,恰恰与欧拉图的定义相违背,自然就证明了欧拉图中不能有桥了。
说完了欧拉图,我们来看哈密顿图。
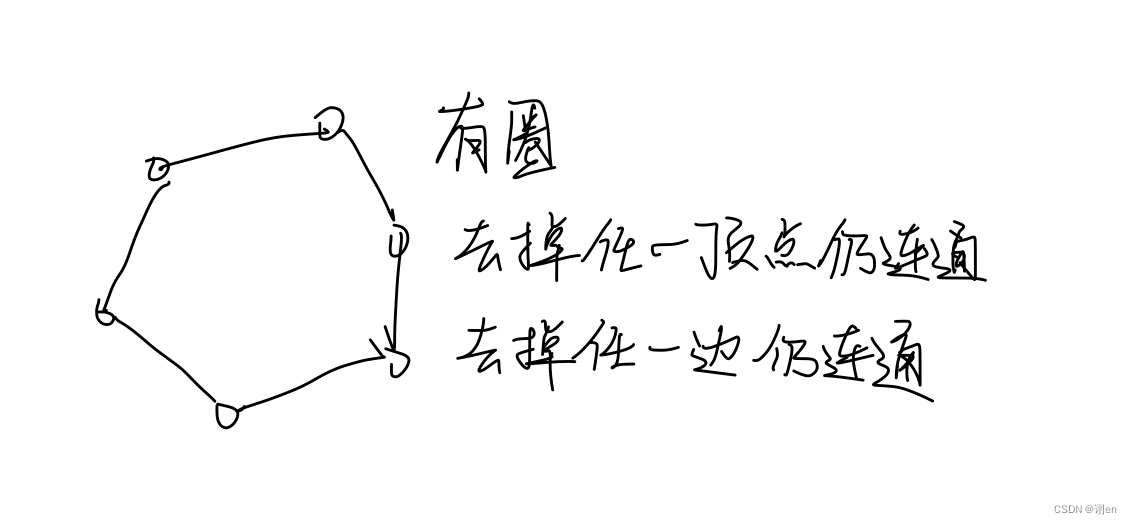
哈密顿图是具有哈密顿圈的图,哈密顿圈是对于图G而言,它有一个圈,这个圈包含了图G的所有顶点。
换言之,如果一个图G,它具有一个能包含所有顶点的圈,那么它具有哈密顿圈,图G也就是哈密顿图了。
显然哈密顿图是有圈的图,有圈的图不论去掉哪个顶点依然是连通的,所以哈密顿图没有割点。有圈的图不论去掉哪条边也依然是连通的,所以哈密顿图也没有桥
换言之,有割点的图一定不是哈密顿图,有桥的图一定不是哈密顿图。
完毕!
