AI学习目录汇总

0、前言

YOLOv1~3作者是约瑟夫·雷德蒙（Joseph Chet Redmon），他的网站：https://pjreddie.com/
YOLOv1网站：https://pjreddie.com/darknet/yolov1/
YOLOv2网站：https://pjreddie.com/darknet/yolov2/
YOLOv3网站：https://pjreddie.com/darknet/yolo/
github：https://github.com/pjreddie/darknet

YOLOv4作者是AlexeyAB（俄），网站：https://github.com/AlexeyAB/darknet
YOLO之父Joseph Redmon因为YOLO被用于军事目的而退出，将衣钵传给了AlexeyAB

YOLOv5作者是ultralytics团队的Glenn Jocher，网站：https://github.com/ultralytics/yolov5
Glenn Jocher并没有发布YOLOv5相关论文，也不被YOLO之父Joseph Redmon认可

YOLOX作者是刘松涛
YOLOX PyTorch实现：https://github.com/Megvii-BaseDetection/YOLOX
YOLOX MegEngine实现：https://github.com/MegEngine/YOLOX
注：MegEngine是旷视深度学习框架天元

YOLOv6是由美团提出的：https://github.com/meituan/YOLOv6

YOLOv7是YOLOv4原开发团队（AlexeyAB等人）的续作，网站：https://github.com/WongKinYiu/yolov7

YOLOv8由ultralytics团队发布：
官网：https://docs.ultralytics.com/
github：https://github.com/ultralytics/ultralytics

1、简介

YOLO：You Only Look Once，一种对象检测算法，2016年由Redmon提出
优点：速度快，适合于实时检测任务；
缺点：准确度略低

2、其它算法对象检测原理

在YOLO出现之前，其它算法使用分类器对测试图像的不同切片进行评估。
例如，使用一个小窗口在图像上滑动来获取一小块图像，称为一块切片，在不同位置切出不同大小的切片后，再对这些切片进行分类处理，可以看成两个任务：找到图片中某个存在对象的区域，然后识别出该区域中具体是哪个对象。

遍历图片中所有可能的位置，地毯式搜索不同大小，不同宽高比，不同位置的每个区域，逐一检测其中是否存在某个对象，挑选其中概率最大的结果作为输出。显然这种方法效率太低。

3、YOLO原理

YOLO将图像分成NxN的格子，同时对每个格子做回归预测，输出每个格子对若干种检测目标的概率、所处的位置等信息。根据概率拼接格子就可以检测出目标的大致轮廓。

4、基本概念

4.1 神经元

神经元基本形式：y = wx + b，以下图为例：

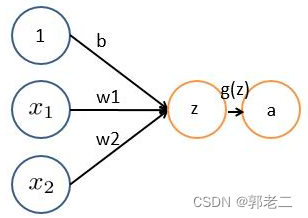
a=g(z) = g( x₁ * w₁ + x₂ *w₂ + b )

• x₁、x₂表示输入向量
• w₁、w₂为权重
• b为偏置bias
• z= x₁ * w₁ + x₂ *w₂ + b 线性组合函数
• g(z) 为激活函数
• a 为输出

4.2 激活函数

为什么要用激活函数？
如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机（Perceptron）。

如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

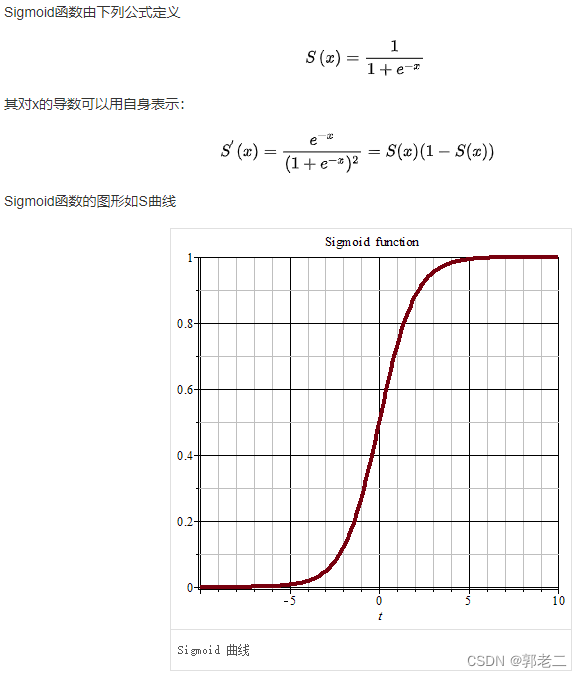
4.2.1 sigmoid

sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点：

• 优点：平滑、易于求导。
• 缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
  

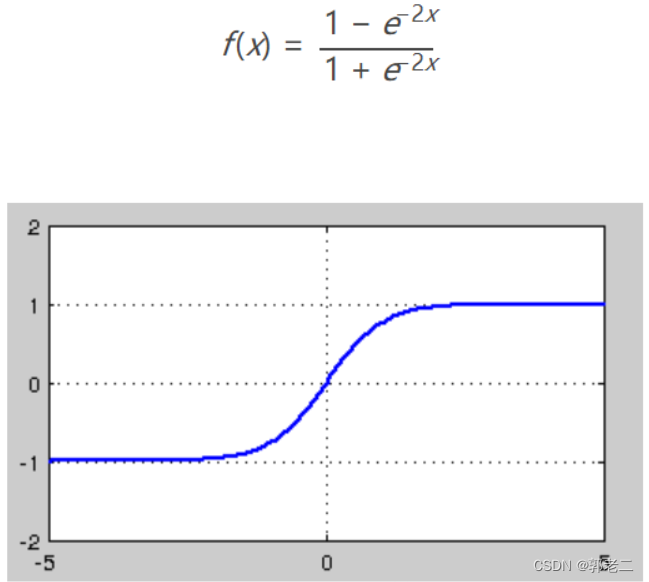
4.2.2 tanh

tanh优缺点：

• 优点：与sigmoid相比，它的输出均值是0，使得其收敛速度要比sigmoid快，减少迭代次数。
• 缺点：tanh一样具有软饱和性，从而造成梯度消失，在两边一样有趋近于０的情况
  

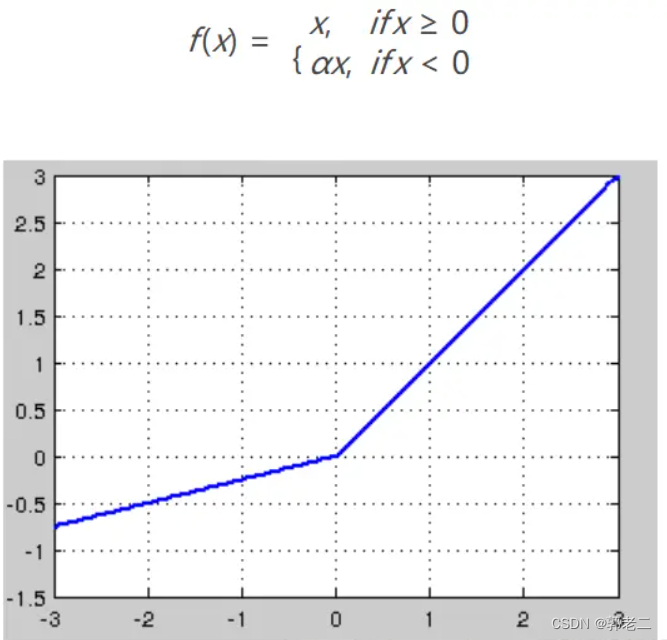
4.2.3 relu

Relu激活函数（The Rectified Linear Unit），用于隐层神经元输出。公式如下

4.3 人工神经网络（DNN）

DNN层级结构如下图所示：包括1，输入层；2.隐含层（1,2，…,n）；3.输出层。层级之间采用全连接（FC），激活函数一般采用sigmoid函数。优化算法一般是随机梯度下降（SGD）

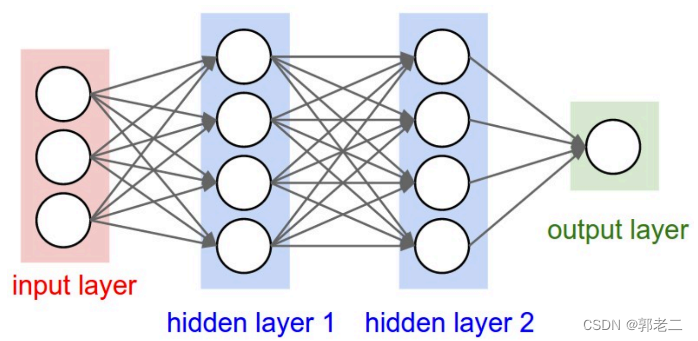
4.4 卷积神经网络（CNN）

4.4.1 什么需要卷积神经网络？

如果用普通的神经网络处理图像，一张图像的数据信息太多，输入层和隐藏层全连接时，将会产生过多的权重，例如，一张图像200x200x3（宽200，高200，颜色RGB通道数3）作为输入，和隐藏层的一个神经元将产生 2002003 = 120,000 个权重。

卷积神经网络以3个维度排列成3D体积的神经元：宽度、高度、深度；一层中的神经元只会连接到它之前的层的一小部分区域，如下图：

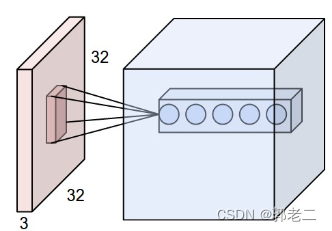
人工神经网络和卷积神经网络对比：

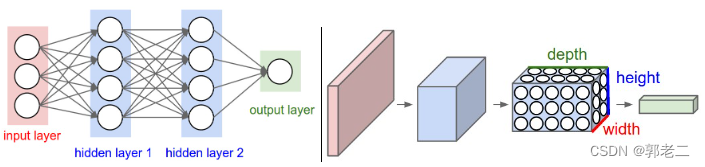
4.4.2CNN层级结构

CNN层级结构如下图所示：包括输入层，若干个（卷积层CONV+激励层（一般使用ReLU激活函数）+池化层（POOL，一般使用最大池化）），最后加一个全连接（FC），预测结果。CNN的每一层都通过可微函数将一个激活量转换为另一个激活量。

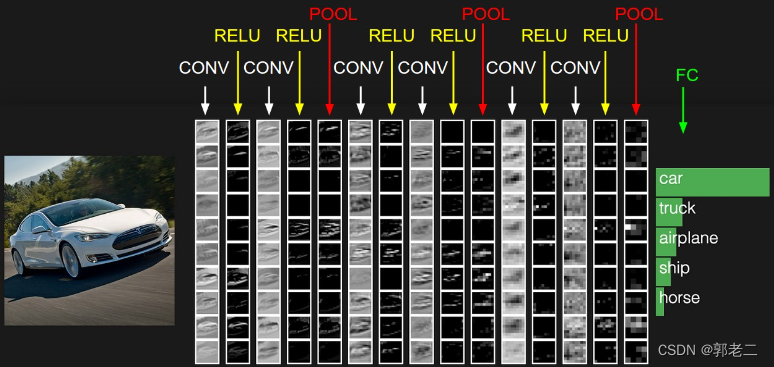
4.5 卷积层CONV

CNN笔记：通俗理解卷积神经网络

4.5.1 什么是卷积层

卷积层（Convolutional layer），卷积神经网络中每层卷积层由若干卷积单元组成，每个卷积单元的参数都是通过反向传播算法最佳化得到的。卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网路能从低级特征中迭代提取更复杂的特征。

4.5.2 超参

输入层的体积（宽、高、深度）受图像像素、色深限制为固定值，卷积层的体积大小怎么确认？
卷积层的体积受三个参数控制，称为超级参数：深度（depth）、步幅（stride）和零填充（zero-padding）

深度（depth）：是指输出量的深度，将一组权重和偏置组成一个过滤器，有n个过滤器，通过卷积运算后将输出n个深度输出量
步幅（stride）：滑动过滤器的步幅。当步幅为 1 时，将过滤器一次移动一个像素；当步幅为 2时，将过滤器一次移动两个像素
零填充（zero-padding）：如果没有零填充，输出的体积将受输入的限制；人为将输入的数据边缘扩充为1个或多个0，可以控制输出体积的空间大小

4.5.3 卷积层体积计算

输入：W1×H1×D1
深度（过滤器）：K
过滤器宽度：F
步幅：S
0填充：P
输出：W2×H2×D2

W2=(W1−F+2P)/S+1
H2=(H1−F+2P)/S+1
D2=K

4.5.4 计算输出

输出层体积中的每个点的值怎么计算？

例如：输入为X，体积为：X.shape: (11,11,4)
过滤器宽度：F = 5
步幅：S = 2
0填充：P = 0
过滤器：W0.shape: (5,5,4)

outV[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
outV[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
outV[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
outV[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0
outV[0,1,0] = np.sum(X[:5,2:5,:] * W0) + b0
outV[1,1,0] = np.sum(X[2:7,2:5,:] * W0) + b0
outV[2,1,0] = np.sum(X[4:9,2:5,:] * W0) + b0
outV[3,1,0] = np.sum(X[6:11,2:5,:] * W0) + b0
……

4.6 激励层：RELU

每个卷积层后都再更一个RELU激活层

4.7 池化层：POOL

4.7.1 池化层作用

池化层夹在连续的卷积层中间， 用于减少数据和参数的个数。

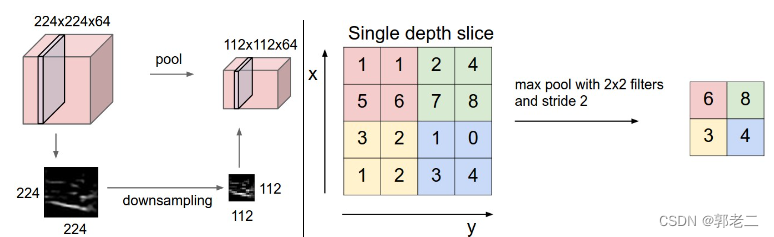
左图：大小为 [224x224x64] 的输入量经过大小为 2 、步幅为2的过滤器处理，输出量为 [112x112x64] 。请注意体积深度被保留。
右图：最常见的过滤操作是取最大值。

4.7.2 池化层体积计算

输入：W1×H1×D1
过滤器宽度：F
步幅：S
输出：W2×H2×D2

W2=(W1−F)/S+1
H2=(H1−F)/S+1
D2=D1

4.7.3 舍弃池化层

偶尔在 CONV 层中使用更大的步幅，来较少参数量，代理池化层的作用，反而训练的更好，例如变分自动编码器 (VAE) 或生成对抗网络 (GAN)。未来的架构可能会很少使用、甚至不再使用池化层。

4.8 全连接层

完全连接层中的神经元与前一层中的所有激活具有完全连接，如常规神经网络中所见。因此，它们的激活可以通过矩阵乘法和偏置偏移来计算。

4.9 过拟合

所谓过拟合(overfitting)，指的是模型在训练集上表现的很好，但是在交叉验证集合测试集上表现一般，也就是说模型对未知样本的预测表现一般，泛化（generalization）能力较差。

4.10 损失函数

每一个样本经过模型后会得到一个预测值，然后得到的预测值和真实值的差值就成为损失（当然损失值越小证明模型越是成功）

最小化损失函数时，只需要使损失函数沿着负梯度前行，就能使损失函数最快下降。
梯度下降用于以最快速度、最少的步骤快速找到损失函数的极小值。

4.11 梯度下降

梯度就是导数；
梯度下降作用是找到函数的最小值所对应的自变量的值（曲线最低点对应x的值）。
梯度下降含义（具体操作）是：改变参数（权重、偏置等）的值使得导数的绝对值变小，当导数小于0时候，我们要让目前参数（权重、偏置等）值大一点点，再看它导数值。当导数大于0时候，我们要让目前参数（权重、偏置等）值减小一点点，再看它导数值。当导数接近0时候，我们就得到想要的自变量参数（权重、偏置等）了。也就是说找到这个算法最佳参数，使得拟合曲线与真实值误差最小

4.12 反向传播

参考：深度学习——反向传播（Backpropagation）

5、YOLOv1

5.1 网络结构

输入层：448×448×3的彩色图片。
卷积层：由若干卷积层和最大池化层组成，用于提取图片的抽象特征。
全连接层：由两个全连接层组成，用来预测目标的位置和类别概率值。
输出层：7×7×30的预测结果。

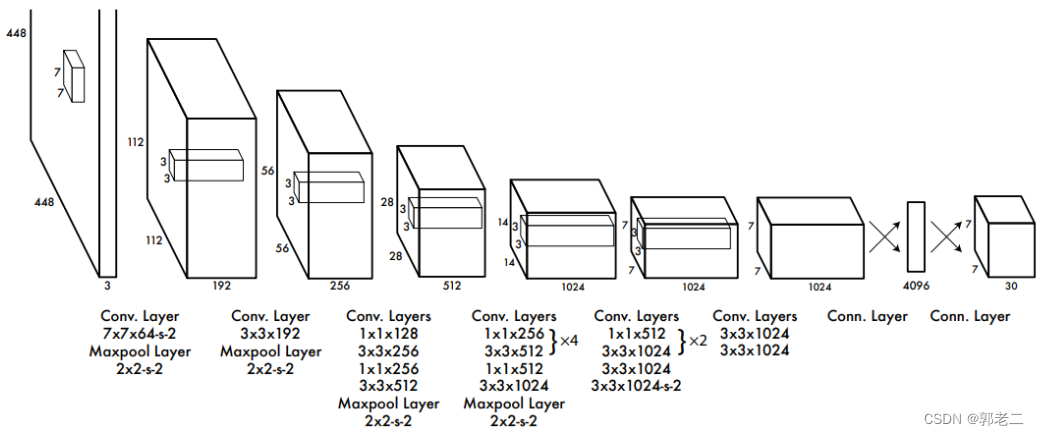
5.2 检测原理

yolo-v1将一幅图像分成的是7x7大小的网格；
yolo-v1要求每个网格预测的是2个边界框（bounding box），每个边界框包含五个值坐标(x,y) 长宽(w,h)和置信度(confidence)

• (x,y) 表示边界框中心 相对于网格 的坐标；
• (w,h) 表示边界框 相对于整张图像 的宽和高
• 意思是边界框的中心坐标必须在网格内，但其宽和高不受网格限制、可以随意超过网格大小
• 当边界框中不存在目标时，置信度应等于0；当边界框中存在目标时，置信度应等于这一边界框和物体的真实边界框的IoU
  
  yolo-v1默认可以预测的类别有20种，每个网格还要预测一个类别信息（C 个类）

​ IoU表示（真实值和预测值的交集）占（真实值和预测值的并集）的比列:

5.3 输出张量

S×S 个网格，每个网格要预测 B个边界框 ，还要预测 C 个类。输出层就是一个 S × S × (5×B+C) 的张量。对于yolo-v1，网络输出即是一个7x7x30的张量

6、YOLOV1的不足

• 每张图片能够进行分类数量太少，只有20种物体分类；
• 检测的目标的数量太少，一张图只能检测 7 * 7 = 49个目标；
• 对重叠在一起的物体检测性不好；
• YOLO对小目标的检测效果不好；