FPGA实现Cordic算法求解arctan和sqr(x*2 + y* 2)
一. 简介
由于在项目中需要使用的MPU6050,进行姿态解算,计算中设计到**arctan 和 sqr(x2 + y 2),**这两部分的计算,在了解了一番之后,发现Cordic算法可以很方便的一次性求出这两个这两部分的计算。另外也可以一次性求出sin和cos的值。另外该算法还可以计算其他的一些公式(没做过多的了解)。
二. Cordic算法
该算法的核心实现就是旋转逼近,每次旋转一定的角度,无限的逼近所给定的角度值。
1. 理论基础
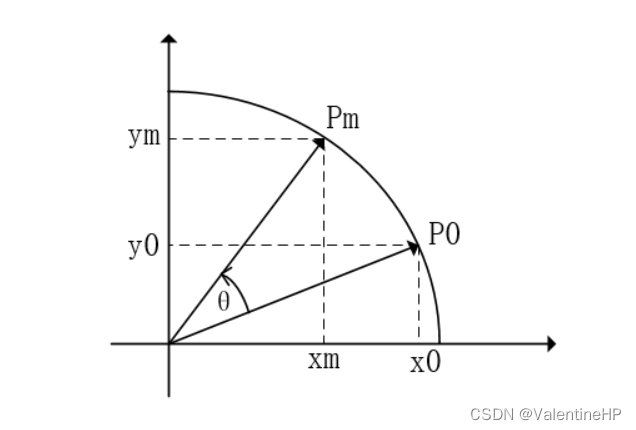
首先有向量P0,现在要将其旋转θ角度,到Pm。 那么Pm的坐标值如下
xm = x0cosθ - y0sinθ = cosθ(x0 – y0tanθ)
ym = x0sinθ + y0cosθ = cosθ(y0 + x0tanθ)
P0和Pm均在单位圆上,另外假设现在P0在X轴上,即 X0 = 1,y0 = 0。上式就可以变为如下显示
xm = x0cosθ - y0sinθ = cosθ
ym = x0sinθ + y0cosθ = sinθ
可以看到Pm的坐标值,就是sinθ 和 cosθ的值。这就是理论基础。
2. sinθ 和 cosθ 算法实现
有了理论支持后,我们只需要求解Pm的坐标即可。直接旋转θ不太可能,但是我们可以每次旋转特定的角度θi (tanθi = 1/2^i),让我们的角度值逼近θ即可。于是就有了如下迭代公式。
x(i+1) = cosθi* (xi – yi * tanθi)
y(i+1) = cosθi * (yi + xi * tanθi)
θ(i+1) = θi (±) dθi
如果当前角度小于设定角度,那么就加dθ ,大于设定角度 , 那么就减dθ。由于每次旋转的dθ,会越来越小,所以旋转的当前角度会越来越来接近设定角度。
计算过程中 ,cosθi,只充当缩放因子,对旋转方向没有影响。可以先在软件中提取技术出来。每次旋转角度值如下。

3. arctan (x,y)和 sqr(x*2 + y * 2)算法实现
在求解sinθ 和 cosθ 的时候,知道,给定一个角度,按照上述方法就可以求解。现在将其反过来,给定sinθ 和 cosθ的值,也就是Pm的坐标(可能不在单位圆上,只是模值缩放了),现在只需要将其旋转到X轴的正半轴上,即Y = 0 ,X > 0的时候,所旋转过的角度值即arctan (x,y)。
然后P0的X坐标值即sqr(x2 + y * 2)。旋转过程中,向量的模值是不会改变的,而Pm的模值就是sqr(x2 + y * 2)。
三. Cordic算法实现
首先将上述角度值,存储到verilog中,需要进行扩大处理。由于tanθi = 1/2^i),所以对应的tanθ也是知道的。在相乘的时候,只需要将对应的数右移对应的位数即可
`define rot0 32'd2949120 //45度*2^16
`define rot1 32'd1740992 //26.5651度*2^16
`define rot2 32'd919872 //14.0362度*2^16
`define rot3 32'd466944 //7.1250度*2^16
`define rot4 32'd234368 //3.5763度*2^16
`define rot5 32'd117312 //1.7899度*2^16
`define rot6 32'd58688 //0.8952度*2^16
`define rot7 32'd29312 //0.4476度*2^16
`define rot8 32'd14656 //0.2238度*2^16
`define rot9 32'd7360 //0.1119度*2^16
`define rot10 32'd3648 //0.0560度*2^16
`define rot11 32'd1856 //0.0280度*2^16
`define rot12 32'd896 //0.0140度*2^16
`define rot13 32'd448 //0.0070度*2^16
`define rot14 32'd256 //0.0035度*2^16
`define rot15 32'd128 //0.0018度*2^16
然后就是迭代过程了,迭代16次足够了。最后的Zn和Xn就是想要结果。
//旋转
genvar i;
generatefor( i = 1 ;i < 17 ;i = i+1)begin: loop2always@(posedge clk or negedge rst_n)beginif( rst_n == 1'b0)beginXn[i] <= 'd0;Yn[i] <= 'd0;Zn[i] <= 'd0;endelse if( cal_delay[i -1] == 1'b1)beginif( Yn[i-1][31] == 1'b0)beginXn[i] <= Xn[i-1] + (Yn[i-1] >>> (i-1));Yn[i] <= Yn[i-1] - (Xn[i-1] >>> (i-1));Zn[i] <= Zn[i-1] + rot[i-1];endelsebeginXn[i] <= Xn[i-1] - (Yn[i-1] >>> (i-1));Yn[i] <= Yn[i-1] + (Xn[i-1] >>> (i-1));Zn[i] <= Zn[i-1] - rot[i-1];endendelsebeginXn[i] <= Xn[i];Yn[i] <= Yn[i];Zn[i] <= Zn[i];endendend
endgenerate
这里没有乘cosθ,最后的Xn会比真实值大1.64倍左右,所以还需要对其进行一个缩小操作,通过右移来近似实现。
assign cordic_ack = cal_delay[16];
assign theta = Zn[16];
assign amplitude = (Xn[16] >>> 1) + (Xn[16] >>> 3); 幅度,偏大1.64倍,这里做了近似处理
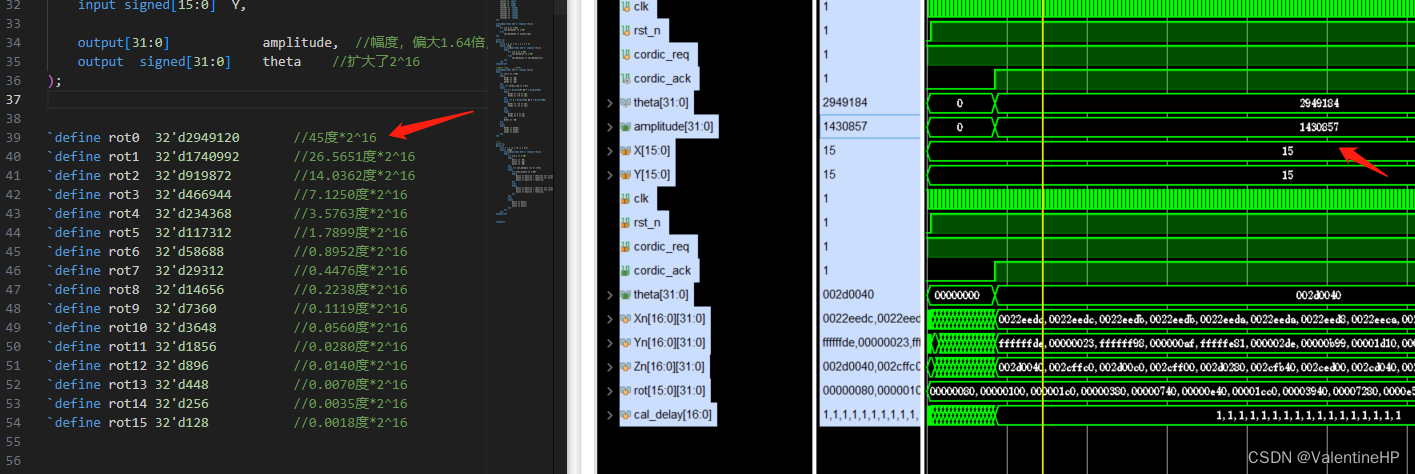
然后就是仿真了,给了X=Y=15,也就是角度为45度,幅值21.213,扩大65536倍为1,376,256。可以看到结果近似。
需要完整文件的可以关注公众号 FPGA之旅,私聊。后面等MPU6050的姿态解算模块完成了再完整上传。
