D1. LuoTianyi and the Floating Islands (Easy Version)(树形dp)
Problem - D1 - Codeforces

这是问题的简化版本。唯一的区别在于在该版本中k≤min(n,3)。只有在两个版本的问题都解决后,才能进行黑客攻击。 琴音和漂浮的岛屿。
洛天依现在生活在一个有n个漂浮岛屿的世界里。这些漂浮岛屿由n−1个无向航线连接,任意两个岛屿之间都可以通过这些航线到达。也就是说,这n个漂浮岛屿形成了一棵树。
有一天,洛天依想见她的朋友:Chtholly、Nephren、William等。她总共想见k个人。她不知道他们的确切位置,但是她知道他们在两两不同的岛屿上。她定义一个岛屿是好的,当且仅当从它到具有k个人的岛屿的距离和为所有n个岛屿中最小的时候。
现在,洛天依想知道,如果将k个人随机放置在n个岛屿中的k个不同的岛屿上,那么好的岛屿的期望数量是多少?你只需要告诉她期望数量模109+7的值。
†
两个岛屿之间的距离是你需要采取的最少的航线数量,以到达另一个岛屿。 输入
第一行包含两个整数n和k(1≤k≤min(n,3),1≤n≤2⋅105) - 岛屿和人的数量。
接下来的n−1行描述了航线。它们中的第i行包含两个整数ui和vi(1≤ui,vi≤n,ui≠vi)-第i条空中路线连接的岛屿。 输出
打印一个整数-好岛屿的期望数字模109+7。
严格地说,让M=109+7。可以证明答案可以表示为不可约分数pq,其中p和q是整数,q≢0(modM)。输出等于p⋅q−1modM的整数。换句话说,输出这样一个整数x,使得0≤x<M且x⋅q≡p(modM)。
Examples
Input
Copy
4 2 1 2 2 3 3 4
Output
Copy
666666674
Input
Copy
5 1 1 2 2 3 3 4 3 5
Output
Copy
1
题解:
对于k = 1的情况,无论这个点在哪,唯一的好点就是其本身,只有一种可能,所以直接输出1
对于k = 3的情况,我们可以先确定一个中间的点,这个点肯定不能在叶子节点上,另外两个点分别放在这个中点两边,我们会发现这样好点只会是中点本身,也输出1
对于k = 2的情况,我们可以发现,这两人在任何两个不同的点上,好点的数量是两个点相连链上的点的数目,我们可以通过单个点对答案的贡献来求
我们在dfs时可以求所有点的子树大小,对于这些点对答案的贡献为,
dp[ne]*(n - dp[ne]),可以理解为右节点在子树中,左节点在子树外,
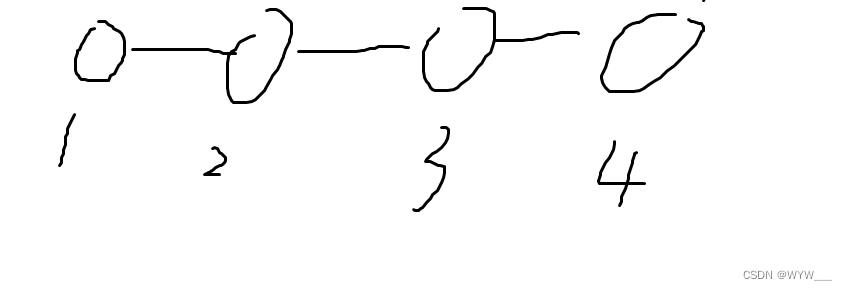
这样计算完,我们得到的好点数是10,而答案是16,显然少了一些贡献,我们多举几个例子就能发现,还要加上n*(n - 1)/2,(至于为啥是这样,想了好长时间,实在想不明白,望大佬帮忙指正)
最后别忘了除概率n*(n - 1)/2,
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define int long long
typedef pair<int,int> PII;
const int N = 3e5 + 10;
int mod = 1e9 + 7;
vector<int> p[300050];
int ans;
int qpow(int x,int y)
{int ans = 1;while(y){if(y&1)ans = ans*x%mod;x = x*x%mod;y /= 2;} return ans;
}
int m,n;
int dp[N];
void dfs(int x,int fa)
{dp[x] = 1;for(auto ne:p[x]){if(ne == fa)continue;dfs(ne,x);dp[x] = dp[x] + dp[ne];ans = (ans + dp[ne]*(n - dp[ne])%mod)%mod;
// cout <<ne <<" "<<dp[ne] <<"\n";}
}
void solve()
{int k;cin >> n >> k;for(int i = 1;i < n;i++){int x,y;cin >> x >> y;p[x].push_back(y);p[y].push_back(x);}if(k == 1||k == 3){cout << 1;}else if(k == 2){m = qpow((n*(n - 1)/2)%mod,mod - 2);dfs(1,0);
// cout << ans ;cout << (ans + (n*(n - 1)/2)%mod)%mod*m%mod;}
}
signed main()
{ios::sync_with_stdio(0 );cin.tie(0);cout.tie(0);int t = 1;
// cin >> t;while(t--){solve(); }
}
