加密与解密
加密与解密
加密方式分类
加密方式主要分为两种
- 一种是对称加密
- 一种是非对称加密
对称加密
对称和非对称两种方式主要说的是加密和解密两个过程。
如果对数据用一个钥匙进行了加密,那么, 你想成功读取到这个加密了的数据的话,就必须对这个加密数据进行解密才行。
在现实生活中,我们锁了门,那就必须用相对应的钥匙才能打开这个门。在数据加密中也是如此,我们对数据进行了加密,也是必须用相对应的钥匙才能解密数据。
因此问题就来了,这种时候我们就会思考怎么对数据进行加密,怎么对数据进行解密。
一开始的方式一般都是比较简单的,就是,我们用一把钥匙对数据进行加密,如果要解密这个数据,就再次用这把钥匙对加密的数据进行解密即可。
像这种加密和解密都是用同一把钥匙的方式就叫做对称加密
采用这种加密方式就诞生了诸多的加密算法,较为常用和知名的就是DES、AES算法

非对称加密
经过上面对对称加密方式的解释,相信聪明的你一定明白了非对称加密方式是怎么回事了吧。简单的说,就是非对称加密的加密和解密的两把钥匙不是同一把钥匙。
但是这里可能大家就会出现一个疑问,因为根据显示生活中的案例来说,既然钥匙都不同了,怎么能解锁呢。
这种时候就不能太较真计算机世界和现实世界的这些小区别了。
这也正是非对称加密算法的特点,就是通过非对称加密算法生成的加密和解密的两把钥匙不同,并且通过加密钥匙加密的数据只能通过解密钥匙解密(相反的,用解密钥匙加密的数据,也只能用解密钥匙进行解密)
一般,我们把通过非对称算法生成的加密钥匙称之为公钥,把通过非对称算法生成的解密钥匙称之为私钥。
而如今常见的非对称算法就是我们现在熟知的RSA算法
思考
为何要有这两种截然不同的加密解密方式?
其实出现这两种截然不同解密解密方式最主要的原因还是因为对称加密的知名缺点
对称加密加密方式的缺点
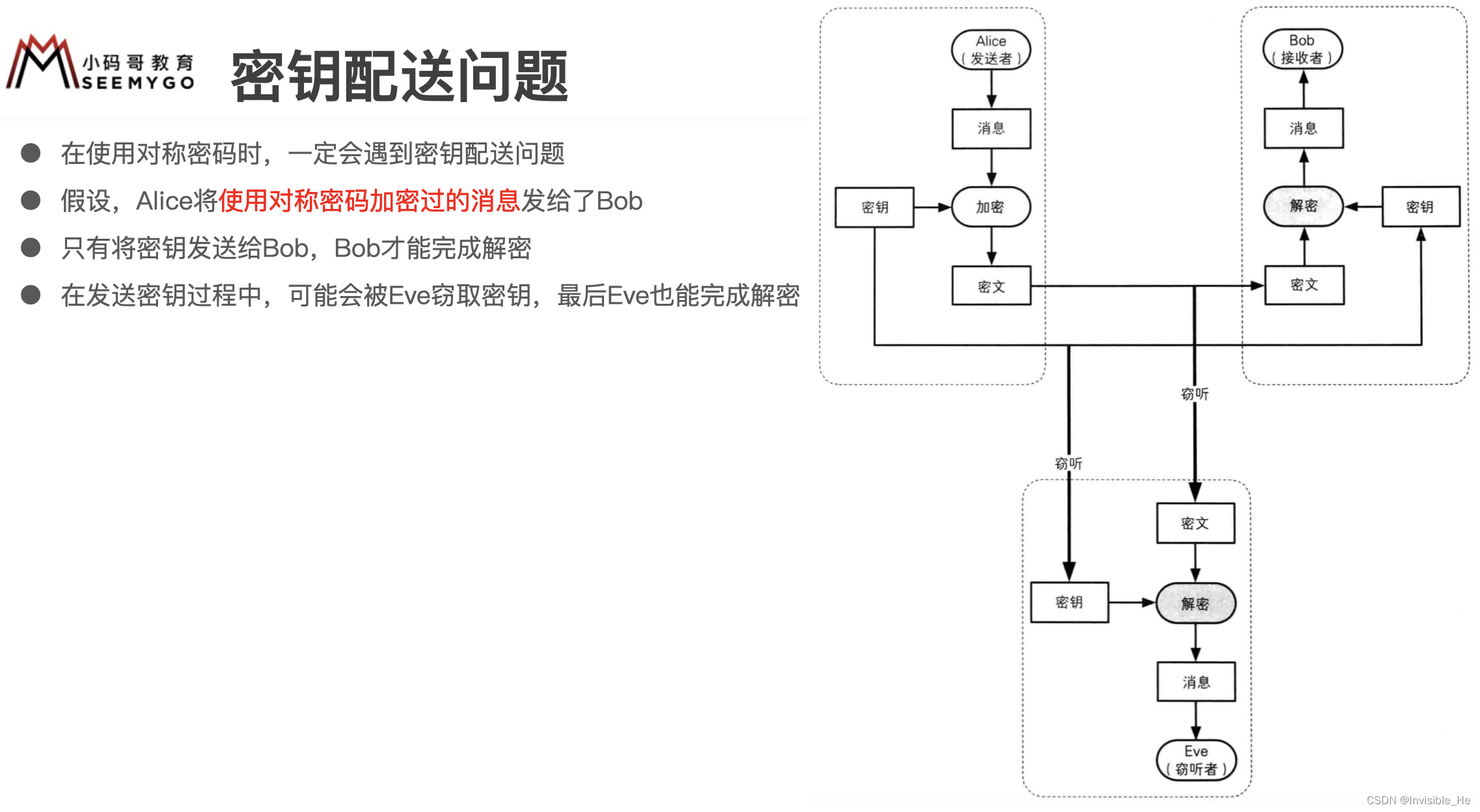
对称加密有个灰常知名的缺点,那就是,因为加密和解密的钥匙是同一把,那么发送者想要接收者能解密数据,就必须把钥匙传输给接收者,这样一来,就可能会存在传输钥匙的过程中被中间人拦截获取的问题。一旦钥匙被劫持获取,加密数据就变得跟没加密的数据一样。
因此,为了解决钥匙传输问题就衍生出了非对称方式
非对称加密方式的优点
非对称加密方式的特点
通过非对称加密算法生成的加密和解密的两把钥匙不同,并且通过加密钥匙加密的数据只能通过解密钥匙解密(相反的,用解密钥匙加密的数据,也只能用解密钥匙进行解密)
正因为这一特点,非对称加密方式就完美解决了钥匙传输问题。
在实际的应用中,数据的接收者通过RSA算法生成公钥和私钥,之后将公钥发送给数据的发送者,私钥自己保留,用着最终的解密数据。
过程是这样的,发送者用公钥将数据加密,之后再将加密后的数据发送给接收者,接收者用自己手中的密钥对加密的数据进行解密即可
因此,即使在公钥传输过程中被劫持了,数据也不可能被公钥解密。这样就完美解决了钥匙传输问题。
因此这也是非对称加密方式的典型优点,就是能避免钥匙的泄露而导致数据泄露

混合加密方式
非对称加密方式的缺点和对称加密方式的优点
世间没有十全十美的东西和实物。对于加密解密方式也是一样的,有优点就有缺点
非对称加密方式的缺点
虽然非对称加密的优点完美解决了钥匙的传输问题,但是非对称加密算法有个不小的缺点,那就是,它对数据的加密解密时间很长
因此,如果在实际应用中,完全用非对称加密方式的话,无疑是效率极低的。大家都明白,效率低是不能容忍的。
对称加密方式的优点
虽然对称加密方式的缺点很明显,但是它的优点亦是很吸引人的,那就是,它的加密效率很高,相对非对称加密方式的话,它的加密速度快很多很多
混合式加密方式的诞生
既然这两种方式都有各自的优缺点,那么我们要做的就是取其精华去其糟粕,各取两种方式的优点,混合使用。这样就能既安全又高效的对数据进行加密解密
加密过程
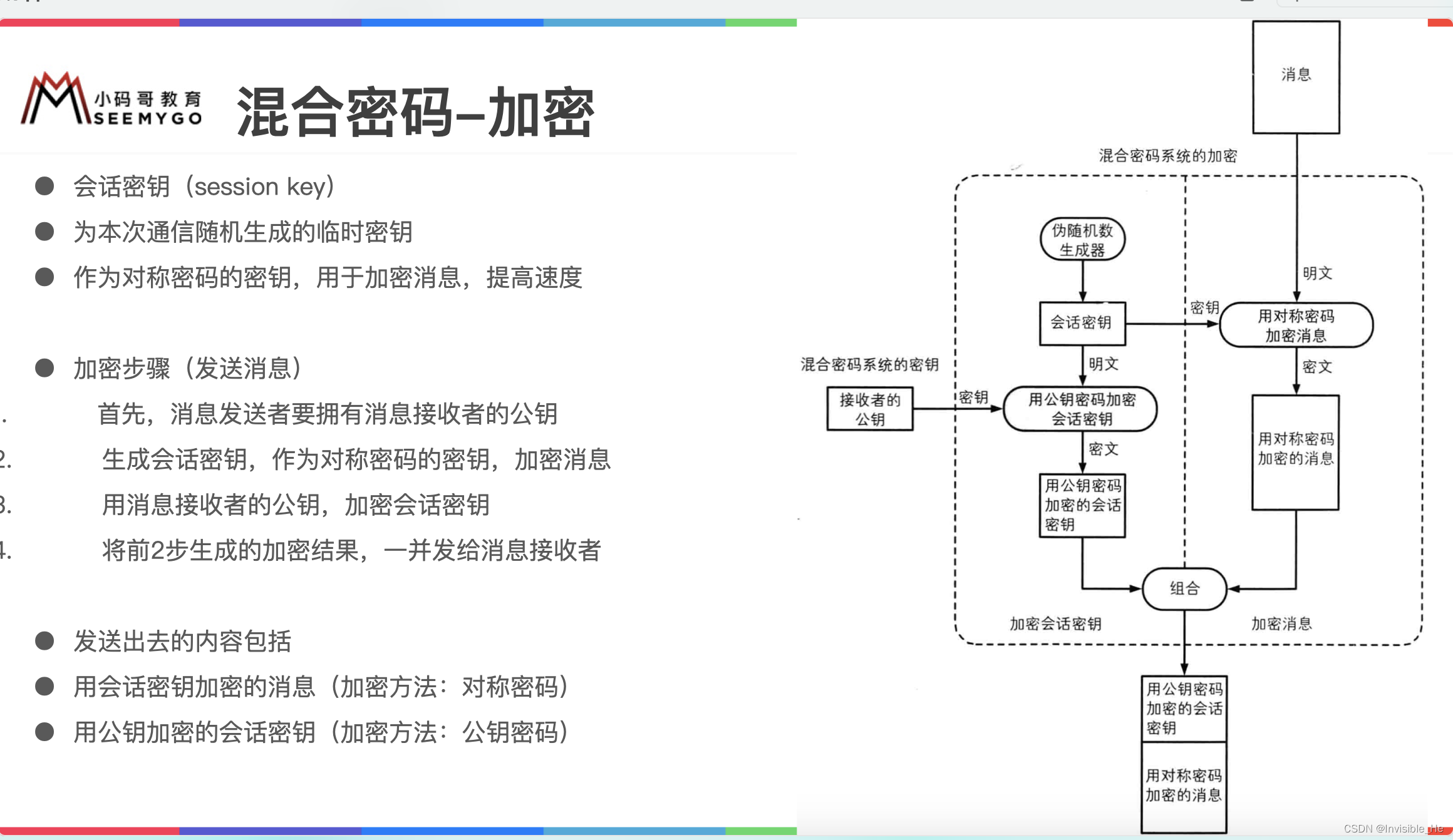
简单说明一下如何混合利用两种方式的优点进行加密
- 1、因为非对称加密慢,因此,我们对数据的加密依然用对称加密方式,这样就能快速的加密数据
- 2、但是对称加密存在钥匙传输问题,但是非对称方式能解决传输问题,因此,就用非对称方式的公钥对 对称加密的钥匙 进行加密
- 3、之后再将加密后的数据和加密后的对称钥匙一并发送给接收者
- 4、之后接收者用非对称方式的密钥对加密后的 对称钥匙 进行解密
- 5、再用解密后的 对称钥匙 对数据进行解密
- 6、这样就做到了, 既能快速加密数据,又能确保钥匙的安全
