这就是二分查找?(C语言版)
大家好!我又来了,哈哈~今天我要和大家分享一种神奇的算法——二分查找!你可能会问,“二分查找有什么好玩的?”但在我看来它就像一场魔法表演,当你输入一个数,他会在一堆数中快速找到它的位置。找不到他还会告诉你这个数不存在数堆中。当然初学C语言的朋友也不要被它的名字所吓到,接下来我将详细的告诉你二分查找原理,及实现初学C的朋友赶快来学习一波吧!
我们前边已经学习了循环,在一个数组中查找一个数,我们可以使用循环遍历,直到找到目标数。但在数据较多的时候一直这样循环的去找,就会大大影响程序效率,这时我们就有了引进了新的方法来改变效率低的问题那就是我们今天要讲的二分查找。
二分查找的原理
举个栗子,假如你一个朋友他买了一双新鞋,你问他多少money,他告诉你不超过1000,那你会怎么猜,从1块,2块,3块……这样的猜吗?这样肯定不合适,那最快的方法就是区间对半的去猜,你说500,他说猜小了,那么这时,区间就减少了一半,你再猜750……就这样一直将区间对半排除的去猜,你就可以在最少的猜测次数内猜到答案。这也就是二分查找的原理。
适用情况
既然二分查找这么厉害,当然它也不是什么情况都能应对的,二分查找只适用于有序的的数据查找(可以是递增,也可以是递减)。
如何实现
我们以及知道了原理,那么要怎样去实现呢?
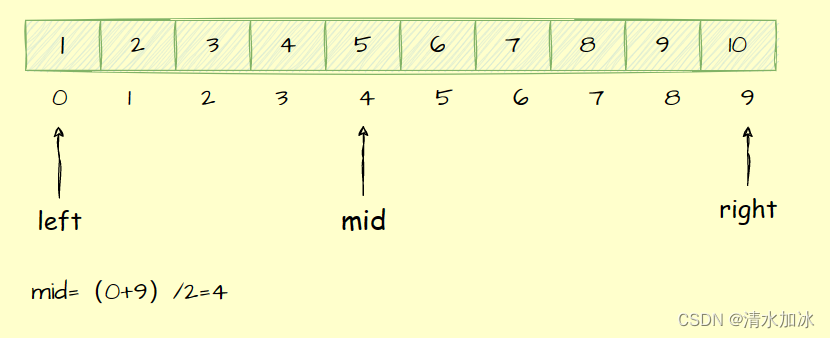
以上图为例,我们创建3个变量,分别记录数组的最左下标,中间下标,最右下标。初始情况下left下标为0,mid下标为4,right下标为9,假设我们要查找的数字是7;
假设第一次输入5,会收到提示:" 猜小了 ",这时查找区间就减少了一半,左下标left也就变为了mid+1(此时left下标为5),而mid是左下标和右下标之间的中间下标,这时mid就变成了7( (5+9)/7,这里是整除哦)如下图:
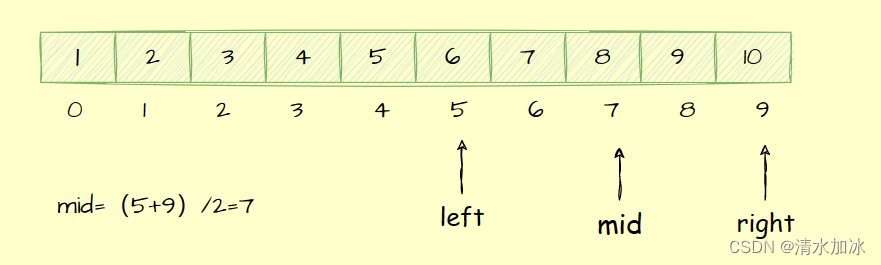
假设第二次输入8,收到提示:" 猜大了 ",右下标right也就变成了mid-1(此时right下标为6),mid就变成了5,如下图:
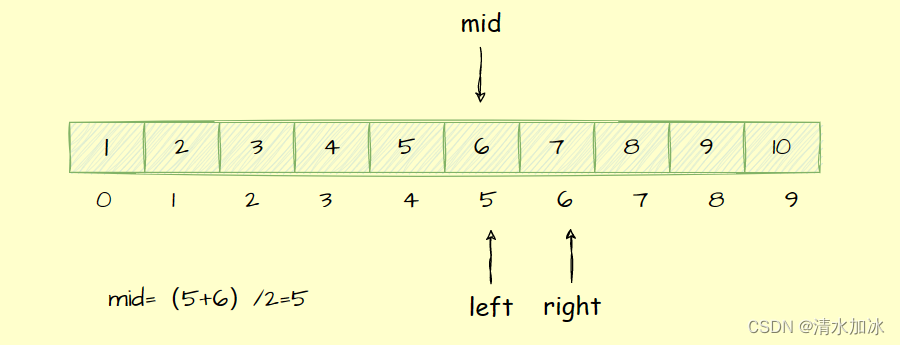
这时就剩下了两个数
假设第三次输入6,继续收到提示:" 猜小了 ",left就变成了mid+1=6,mid=(6+6)/2=6,最后就只剩下了一个7。
最后输入7,提示:“找到了,下标为6”。
代码实现二分查找的整体思路大概就是以上这样;
代码实现
接下来我们进行代码实现:
#include<stdio.h>
int main()
{int arr[] = { 1,2,3,4,5,6,7,8,9,10 };int k = 7;int sz = sizeof(arr) / sizeof(arr[0]);int right = sz - 1;int left = 0;int flag = 0;while (left <= right) {int mid = (left + right) / 2;if (arr[mid] == k) {printf("找到了,下标是%d",mid);flag++;break;}else if (arr[mid] > k) {right = mid - 1;}else {left = mid + 1;}}if (flag == 0)printf("没找到\n");return 0;
}好了本期内容到这里就结束了,希望对你所帮助,感谢阅读,我们下期再见!
