[创新工具和方法论]-01- DOE课程基础知识
文章目录
- 1.DOE实验设计的介绍
- 1.1 什么是实验设计DOE?
- 1.2 DOE的优势有哪些?
- 1.3 如何开展DoE研究?
- 步骤
- 2.DOE实验培训
- 3.数据分析步骤
- 4.实验的随机化
- 5.偏差
- 6.R方 相关系数
- 假设检验
- 7.三因子二水平全因子设计
1.DOE实验设计的介绍
实验设计是一种安排实验和分析实验数据的数理统计方法。实验设计(DOE)是开发实验策略的工具,该策略可以使用最少的资源来最大程度地提高学习效果。DOE被广泛应用于许多领域,并在所有自然科学和社会科学中得到广泛应用。
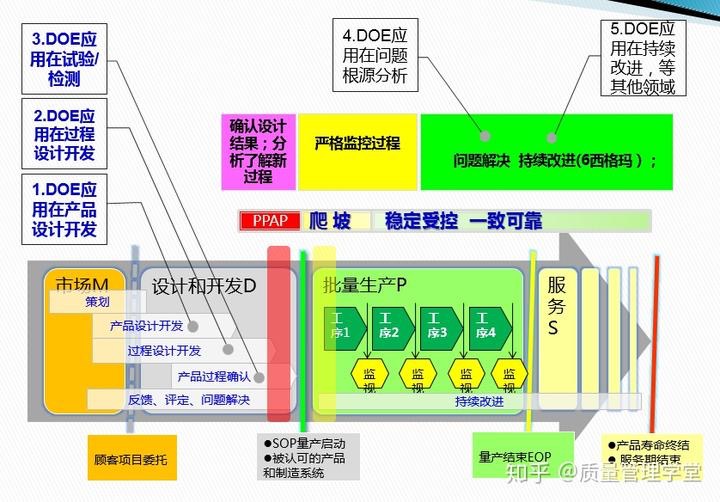
1.1 什么是实验设计DOE?
实验设计(DoE)是一种优化反应和工艺的统计方法,允许不同因素同时发生变化,以便筛选出反应空间的较佳值。
在化学开发领域,由于实验设计(DoE)能使用少量实验评估大量反应参数,其已然成为一种加快反应优化的标准方法。 过去数年间,DoE一直被用于实施研发和制造领域的“质量源于设计”(QbD)。 在制药行业的QbD中,了解产品和工艺对确保产品生产质量至关重要。
1.2 DOE的优势有哪些?
由于DoE研究通常无需多次重复实验,因此DoE具有以下优势:
1).在更短的时间内更好地了解工艺
2).缩短制造领域的开发周期
1.3 如何开展DoE研究?
步骤
- 陈述实际的问题和实验的目的;
- 因果链分析,提取重要的因子;
- 选择Y的响应变量
- 陈述因子和水平
- 选择DOE实验设计
- 实施实验以及收集数据
- 分析实验结果
- 结论和计划
2.DOE实验培训
- 单因子实验法
- 正交实验:
- 判段x对于y的影响最大的
- 包括可控和不可控的x
- 明确关键性的工程和噪声变量
- 明确过程中需要仔细控制的变量
- 实验设计:
- x1的主效应: 高水平下y的均值- 低水平下y的均值
- 交互效应: 一个变量x1会影响x2对因变量的贡献度;也就是在x1在高水平和低水平不同的状态下,x2对y的贡献度不同.也叫协同效应.
3.数据分析步骤
- 实验数据检查
- 模型步骤拟合
- 提出非显著项
- 模型重新拟合
- 模型诊断
- 解释模型/验证
4.实验的随机化
- 重新排列顺序,消除或减小不可控因子的影响;
- 尽量减少本次实验不受前一次实验影响或者不影响下一次实验,保证实验的对立性;
- 实验次数大于系数个数25%至少 ,4个系数 拟合实验至少5次
- 验证实验25%-50%,4个系数 拟合实验至少2次
5.偏差
- 正态分布
- 随机性
- 均匀性
- 偏差=真实值-预测值
6.R方 相关系数
- R^2 = SSR/SST = (SST-SSE)/SST = 1- SSE/SST 尽量接近1 表明模型越好.
- 偏差为0,4个系数求解,做了4组实验,刚好求解4个系数
- 调整R^2 = 1- ((nn-1)/(n-p))(1-r)
假设检验
假设x1的系数等于0,很大的概率支持a=0,所以删除ax1这一项.
7.三因子二水平全因子设计
- 截距+三个主项+二阶交互项+三阶交互项(忽略,认为不显著)
