两道链表经典算法题---链表有无环(基础+进阶)
生活就像一盒巧克力,你永远不知道你会得到什么。——《阿甘正传》

目前自己粗略的学完数据结构,正在开始刷算法题目。个人觉得算法是一个积累,循序渐进的的过程,需要不断加量,进而达到所谓的质。
链表作为数据结构一个重要的分支。我们没有理由不学好它,并且没有理由不刷一些链表的算法题。所以,今天想和大家讲解一下链表有无存在环的经典题目,并且由这道题目本身知识点发散开来,进而来解决一道有无环的进阶题目。看完这一篇文章,你的收获一定会非常之大。看完理解其中的原理之后,你只想说:秒,牛,我靠还能这样,·······,甚至你会直接关注我,给我点个赞。
目录:
一.判断链表是否有环
1.双指针作用(铺垫)
2.结论:环形链表的环一定在末尾,末尾没有NULL
3.具体步骤思路
4.详细代码
二.链表中环的入口节点
1.思路
2.两个结论:
4.详细代码
一.判断链表是否有环
先把题目给到大家,大家可以浏览一下:
1.双指针作用(铺垫)
双指针的作用:由于单向链表(如上图)的每一个指针只能从头往后扫描,并不能从后往前的这一个局限性。所以,我们在解决单向链表的题目上,引入双指针。双指针指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个指针(特殊情况甚至可以多个),两个指针或是同方向访问两个链表,或是同方向访问一个链表(快慢指针)、或是相反方向扫描(对撞指针),从而建立一种手段,让这种手段为我们的目的服务。
2.结论:环形链表的环一定在末尾,末尾没有NULL
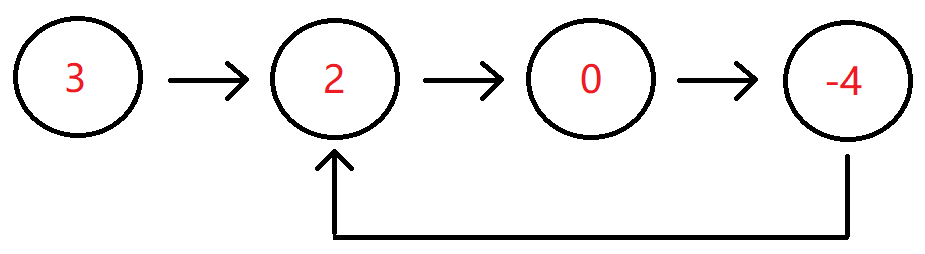
证明:看上图,在环2,0,-4中,没有任何一个节点可以指出环,它们只能在环内不断循环,链表不像二叉树,每个节点只有一个val值和一个next指针,也就是说一个节点只能有一个指针指向下一个节点,不能有两个指针。因此环后面不可能还有一条尾巴。如果是普通链表末尾一定有NULL(第一个图),那我们可以根据链表中是否有NULL判断是不是有环。
3.具体步骤思路
step 1:设置快慢两个指针,初始都指向链表头。
step 2:遍历链表,快指针每次走两步,慢指针每次走一步。
step 3:如果快指针到了链表末尾,说明没有环,因为它每次走两步,所以要验证连续两步是否为NULL。
step 4:如果链表有环,那快慢双指针会在环内循环,因为快指针每次走两步,因此快指针会在环内追到慢指针,二者相遇就代表有环。
·对于step4的进一步解释(个人理解):我们可以这样想,这个快指针一次是走两步,然后慢指针一次走一步,两指针距离会拉大,每循环一次两个指针的距离就会+1,我们假设在遇到环的那一刻他们之间的距离就是n,这时候慢指针在后面,快指针在这个环做周期性走动,慢指针就一步一步的跟上这个快指针,也就是这个n以减1的速度一直在靠近0,直到n=0,这个时候快慢指针就相遇。就能够判断链表有环。
画图解释,看下图:
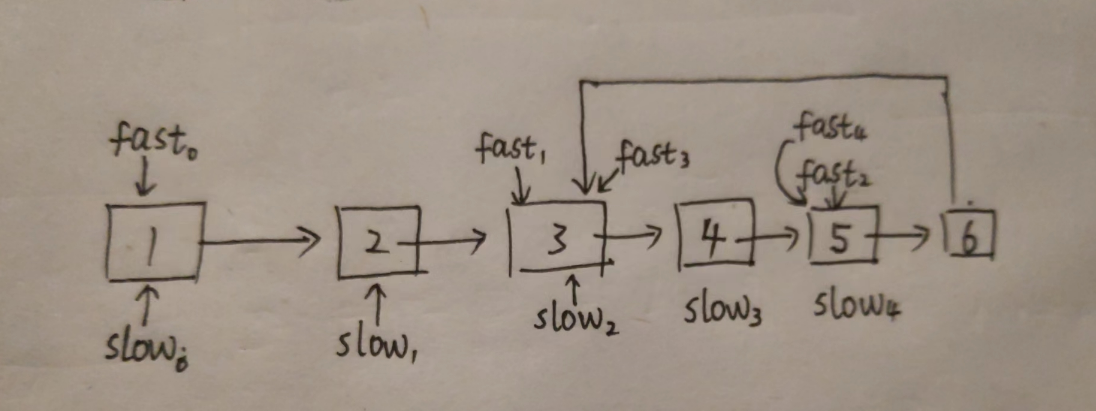
快指针走两步,慢指针走一步,最后相遇。一步一步分析。
4.详细代码
前面都是理论,接下来用代码实现:
#include <stdbool.h>struct ListNode {int val;struct ListNode *next;};//定义一个结点
bool hasCycle(struct ListNode* head )/返回类型是bool
{struct ListNode*fast=head;struct ListNode*slow=head;while(fast!=NULL&&fast->next!=NULL){fast=fast->next->next;//快指针走两步slow=slow->next;//慢指针走一步if(slow==fast)//如果相遇,则有环{return true;}}return false;
}二.链表中环的入口节点
在上一道题目的基础上,我们再来搞定这一道进阶题目:

1.思路
设置快慢指针,都从链表头出发,快指针每次走两步,慢指针一次走一步,假如有环,一定相遇于环中某点(结论一)。接着让两个指针分别从相遇点和链表头出发,两者都改为每次走一步,最终相遇于环入口(结论二)。以下是两个结论证明:
2.两个结论:
结论一:设置快慢指针,假如有环,他们最后一定相遇。
证明:设置快慢指针fast和slow,fast每次走两步,slow每次走一步。假如有环,两者一定会相遇(因为slow一旦进环,可看作fast在后面追赶slow的过程,每次两者都接近一步,最后一定能追上)。也即第一道题的结论。
结论二:两个指针分别从链表头和相遇点继续出发,每次走一步,最后一定相遇与环入口。
证明:设:
链表头到环入口长度为--a
环入口到相遇点长度为--b
相遇点到环入口长度为--c
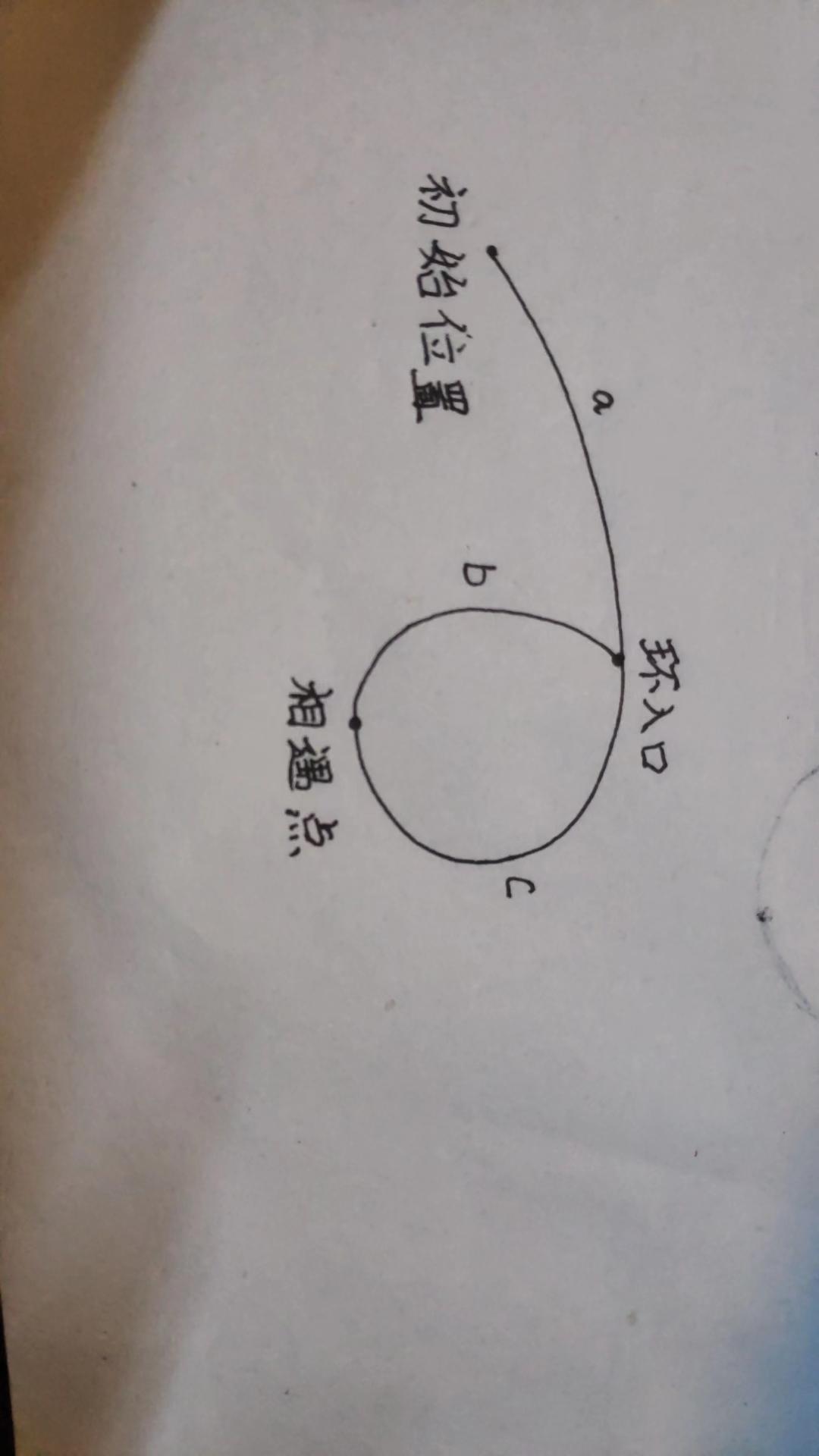
则:相遇时
快指针路程=a+(b+c)k+b ,k>=1 其中b+c为环的长度,k为绕环的圈数(k>=1,即最少一圈,不能是0圈,不然和慢指针走的一样长,矛盾)。
慢指针路程=a+b
快指针走的路程是慢指针的两倍,所以:
(a+b)*2=a+(b+c)k+b
化简可得:
a=(k-1)(b+c)+c 这个式子的意思是: 链表头到环入口的距离=相遇点到环入口的距离+(k-1)圈环长度。其中k>=1,所以k-1>=0圈。所以两个指针分别从链表头和相遇点出发,最后一定相遇于环入口。
4.详细代码
前面都是理论,接下来用代码(C++)实现:
class Solution {
public:ListNode* EntryNodeOfLoop(ListNode* pHead) {ListNode*fast=pHead;ListNode*slow=pHead;while(fast!=nullptr&&fast->next!=nullptr){fast=fast->next->next;slow=slow->next;if(fast==slow)break;}if(!fast||!fast->next)return nullptr;slow=pHead;while(slow!=fast){fast=fast->next;slow=slow->next;}return slow;}
};以上是两道很经典的题目,就讲解到这里。
哦,对了,刚刚在构思这篇文章的过程中突然想到今天是情人节,然后然后,脑子里突然想起,正在看这篇文章的你可能你还没对象,所以呢哈哈哈,下一篇文章要讲解关于C++中new这类知识点,最后new一个自己想要的理想对象致敬在座的每个人。关记得关注我,下一篇今晚就发。

