JavaScript 检查给定的四个点是否形成正方形（Check if given four points form a square）

 给定平面上四个点的坐标，判断这四个点是否形成正方形。 

例子：

输入： p1 = { 20, 10 }, p2 = { 10, 20 }, p3 = { 20, 20 }, p4 = { 10, 10 }

输出：是

解释： 

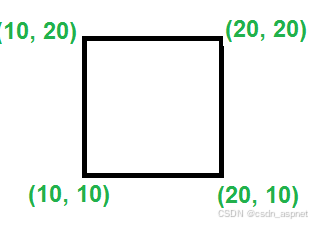
输入： p1 = { 20, 20 }, p2 = { 10, 20 }, p3 = { 20, 20 }, p4 = { 10, 10 }

输出： 否 

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。 

要判断正方形是否为正方形，我们需要检查以下几点。
a ) 由点构成的四条边是否相等。
b ) 任意两条边之间的夹角为 90 度。（此条件是必需的，因为菱形的边也相同。）
c ) 检查两条对角线的距离是否相等

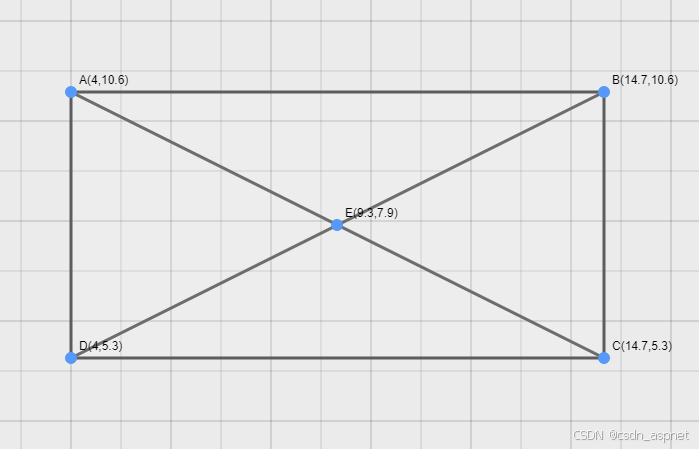
思路是选取任意一点，计算它与其他点的距离。设选取的点为 p。为了构成正方形，两个点到 p 的距离必须相等，设该距离为 d。其中一个点到 p 的距离必须不同于 d，并且必须等于 √2 乘以 d（或者距离平方等于 2 * d ²）。设这个距离不同的点为 q。 

上述条件不够好，因为距离不同的点可能位于另一侧。我们还需要检查 q 与另外两点的距离是否相同，并且该距离是否与 d 相同。

在下面的代码中，为了简单起见，我们将距离计算为 (x1-x2)² + (y1-y2)²。我们不会对其进行平方根运算！

示例代码：

// JavaScript program to check if four given points form a square or not.

// A utility function to find square of distance
// from point 'p' to point 'q'
function distSq( p, q){
    return (p.x - q.x) * (p.x - q.x) + (p.y - q.y) * (p.y - q.y);
}

// This function returns true if (p1, p2, p3, p4) form a
// square, otherwise false
function isSquare(p1,  p2,  p3, p4){
    let d2 = distSq(p1, p2); // from p1 to p2
    let d3 = distSq(p1, p3); // from p1 to p3
    let d4 = distSq(p1, p4); // from p1 to p4

    if (d2 == 0 || d3 == 0 || d4 == 0)    
        return false;

    // If lengths if (p1, p2) and (p1, p3) are same, then
    // following conditions must met to form a square.
    // 1) Square of length of (p1, p4) is same as twice
    // the square of (p1, p2)
    // 2) Square of length of (p2, p3) is same
    // as twice the square of (p2, p4)

    if (d2 == d3 && 2 * d2 == d4
        && 2 * distSq(p2, p4) == distSq(p2, p3)) {
        return true;
    }

    // The below two cases are similar to above case
    if (d3 == d4 && 2 * d3 == d2
        && 2 * distSq(p3, p2) == distSq(p3, p4)) {
        return true;
    }
    if (d2 == d4 && 2 * d2 == d3
        && 2 * distSq(p2, p3) == distSq(p2, p4)) {
        return true;
    }

    return false;
}

// Driver program to test above function
let p1 = { x:20, y:10 }
let p2 = { x:10, y:20 }
let p3 = { x:20, y:20 }
let p4 = { x:10, y:10 }
isSquare(p1, p2, p3, p4) ? console.log("Yes") : console.log("No");

输出：

Yes

时间复杂度： O(1)，所有操作均在 O(1) 常数时间内完成。

辅助空间： O(1)，无需额外空间。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。