代码随想录Day56:图论(冗余连接、冗余连接II)
一、实战
108冗余连接
108. 冗余的边
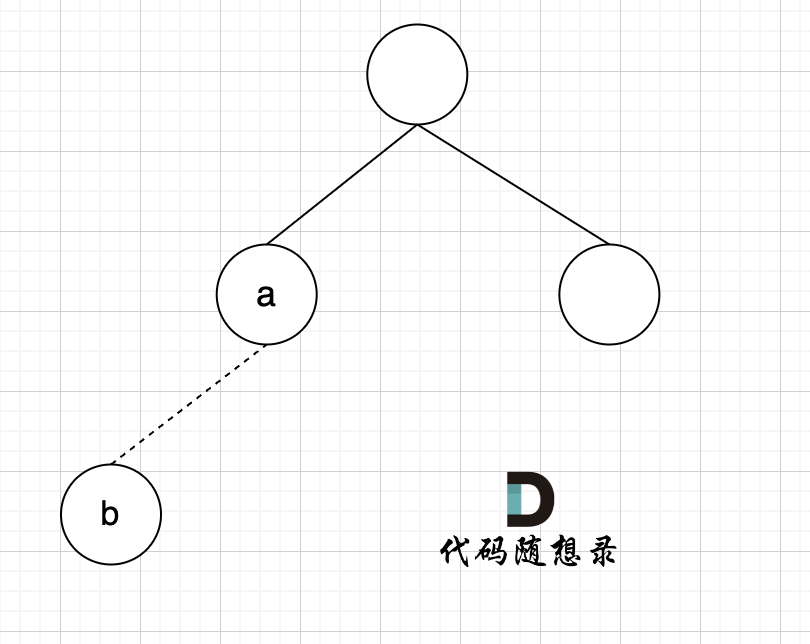
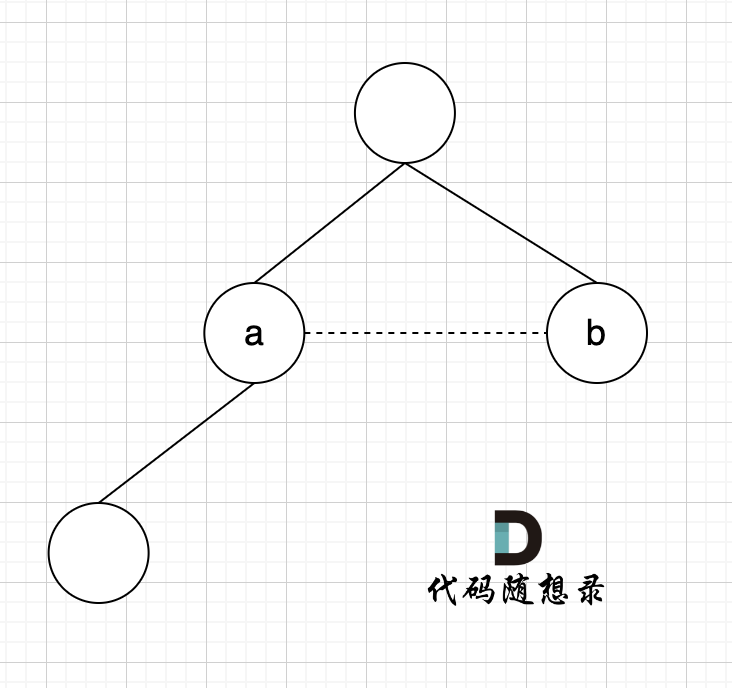
思路:本题需要注意的是在本来就构成树的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,那我们寻找冗余的边,那必然就只有一条。如果有多个答案,则返回二维数组中最后出现的边。
并查集功能:判断两个节点是否在一个集合,也可以将两个节点添加到一个集合中。
那么我们就可以从前向后遍历每一条边(因为优先让前面的边连上),边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
package org.example;//运行时去掉import java.util.*;public class Main{public static void main(String[] args) {int N;int a,b;//构成边的两个节点Scanner scanner = new Scanner(System.in);N = scanner.nextInt();DisJoint disJoint = new DisJoint(N + 1);for (int i = 0; i < N; i++){a=scanner.nextInt();b=scanner.nextInt();if(disJoint.isSame(a,b))System.out.println(a+" "+b);else//不在同一个集合中,那就可以正常添加disJoint.join(a,b);}}}//并查集模板
class DisJoint{private int[] father;public DisJoint(int N) {father = new int[N];for (int i = 0; i < N; ++i){father[i] = i;}}public int find(int n) {return n == father[n] ? n : (father[n] = find(father[n]));}public void join (int n, int m) {n = find(n);m = find(m);if (n == m) return;father[m] = n;}public boolean isSame(int n, int m){n = find(n);m = find(m);return n == m;}}109冗余连接II
109. 冗余的边II
思路:与上一题相比,本题是一个有向图。本质是一个有向图,是由一颗有向树 + 一条有向边组成的 (所以此时这个图就不能称之为有向树),现在让我们找到那条边 把这条边删了,让这个图恢复为有向树。还有“若有多条边可以删除,请输出标准输入中最后出现的一条边”,这说明在两条边都可以删除的情况下,要删顺序靠后的边!
有向树的性质:只有根节点入度为0,其他节点入度都为1(因为该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点)。
情况一:如果我们找到入度为2的点,那么删一条指向该节点的边就行了。
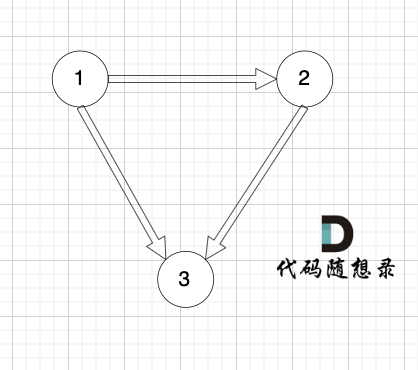
情况二:入度为2 还有一种情况,只能删特定的一条边
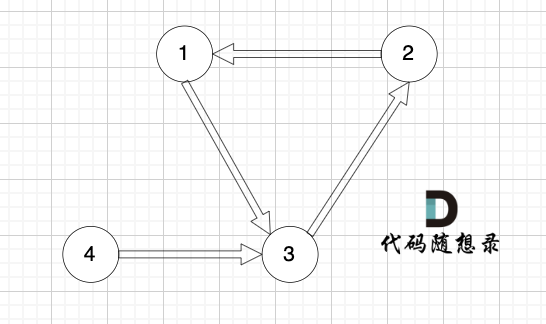
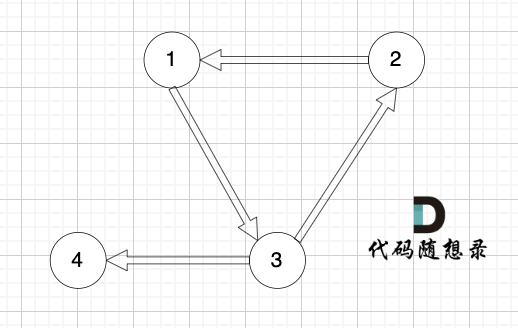
情况三: 如果没有入度为2的点,说明 图中有环了(注意是有向环)。
import java.util.*;public class Main {/*** 并查集模板*/static class Disjoint {private final int[] father;public Disjoint(int n) {father = new int[n];for (int i = 0; i < n; i++) {father[i] = i; // 初始化每个节点的父节点为其自身}}public void join(int n, int m) {n = find(n); // 查找n的根节点m = find(m); // 查找m的根节点if (n == m) return; // 如果根节点相同,则它们已经在同一个集合中father[n] = m; // 将n的根节点指向m的根节点,合并两个集合}public int find(int n) {return father[n] == n ? n : (father[n] = find(father[n])); // 路径压缩优化}public boolean isSame(int n, int m) {return find(n) == find(m); // 判断两个节点是否属于同一个集合}}static class Edge {int s;int t;public Edge(int s, int t) {this.s = s; // 边的起点this.t = t; // 边的终点}}static class Node {int id;int in; // 入度int out; // 出度(在这个问题中未使用)public Node() {in = 0;out = 0;}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 输入节点数量nList<Edge> edges = new ArrayList<>();Node[] nodeMap = new Node[n + 1]; // 创建一个数组来存储每个节点的信息for (int i = 1; i <= n; i++) {nodeMap[i] = new Node();}Integer doubleIn = null; // 记录是否存在入度为2的节点// 遍历输入的所有边,记录每条边,并计算每个节点的入度for (int i = 0; i < n; i++) {int s = scanner.nextInt(); // 边的起点int t = scanner.nextInt(); // 边的终点nodeMap[t].in++; // 增加t节点的入度if (!(nodeMap[t].in < 2)) doubleIn = t; // 如果某个节点的入度达到2,记录该节点Edge edge = new Edge(s, t);edges.add(edge); // 将边加入到列表中}Edge result = null;// 如果存在入度为2的节点,则需要检查并解决这个问题if (doubleIn != null) {List<Edge> doubleInEdges = new ArrayList<>();for (Edge edge : edges) {if (edge.t == doubleIn) doubleInEdges.add(edge); // 找出入度为2的节点相关的边if (doubleInEdges.size() == 2) break; // 只需要找到两条边即可}Edge edge = doubleInEdges.get(1);// 检查移除某一边后,是否可以形成树if (isTreeWithExclude(edges, edge, nodeMap)) {result = edge;} else {result = doubleInEdges.get(0);}} else {// 如果没有入度为2的节点,则只需检查是否存在环result = getRemoveEdge(edges, nodeMap);}System.out.println(result.s + " " + result.t); // 输出需要删除的边}// 检查移除指定边之后,剩余的边能否构成一棵树public static boolean isTreeWithExclude(List<Edge> edges, Edge excludeEdge, Node[] nodeMap) {Disjoint disjoint = new Disjoint(nodeMap.length + 1);for (Edge edge : edges) {if (edge == excludeEdge) continue; // 跳过要排除的边if (disjoint.isSame(edge.s, edge.t)) {return false; // 如果发现环,则不能构成树}disjoint.join(edge.s, edge.t); // 合并两个节点}return true;}// 检查图中是否存在环,并返回导致环出现的边public static Edge getRemoveEdge(List<Edge> edges, Node[] nodeMap) {int length = nodeMap.length;Disjoint disjoint = new Disjoint(length);for (Edge edge : edges) {if (disjoint.isSame(edge.s, edge.t)) return edge; // 发现环则返回这条边disjoint.join(edge.s, edge.t); // 合并两个节点}return null;}
}