Codeforces 斐波那契立方体

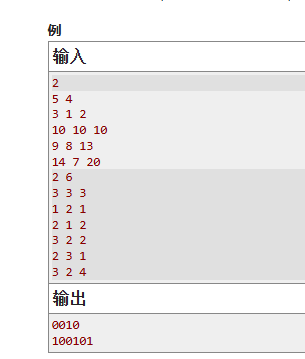
这道题其实不用深究，题目上说每个方块大小都遵循斐波那契数列，那么我们只需要做两个判断是否能塞入题目所给的盒子。

判断1：输入盒子的长宽高后排序，然后将最短的那条边和最大的方块边长比较，如果最短边小于最大的方块，那么肯定不能塞进去，字符串+0

判断2：将最长边减去最大的方块边长后判断第二大道方块边长，因为如果可以塞进去大方块没有多余的位置可以塞小方块那么同样不能满足题意，如果小于，字符串+0

以上只需判断这两个，因为每个方块的边长都要比上一个方块小，那么剩余的空隙是绝对支持放下其他方块的，就像是一根木棍每次只取1/2，是绝对取不完的，同理，小方块的位置也是绝对够放的，所以只需要判断这两个条件，都满足那么就证明这个盒子可以放入所有的方块，字符串+1.

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{int t;cin>>t;while(t--){string stl="";int n,m;cin>>n>>m;vector<int>b(n+5);b[1]=1,b[2]=2;for(int i=3;i<=n;i++){b[i]=b[i-2]+b[i-1];}while(m--){vector<int>a;for(int i=0;i<3;i++){int x;cin>>x;a.push_back(x);}sort(a.begin(),a.end());/*if(a[0]>=b[n-1]&&a[1]>=b[n-1]&&a[2]>=b[n]){stl=stl+'1';}else{stl=stl+'0';}*/if(a[0]<b[n]){stl=stl+'0';continue;}if(a[2]-b[n]<b[n-1]){stl=stl+'0';continue;}stl=stl+'1';}cout<<stl<<endl;}return 0;}