大模型的底层运算线性代数
深度学习的本质是用数学语言描述并处理真实世界中的信息,而线性代数正是这门语言的基石。它不仅提供了高效的数值计算工具,更在根本上定义了如何以可计算、可组合、可度量的方式表示和变换数据。
1 如何描述世界
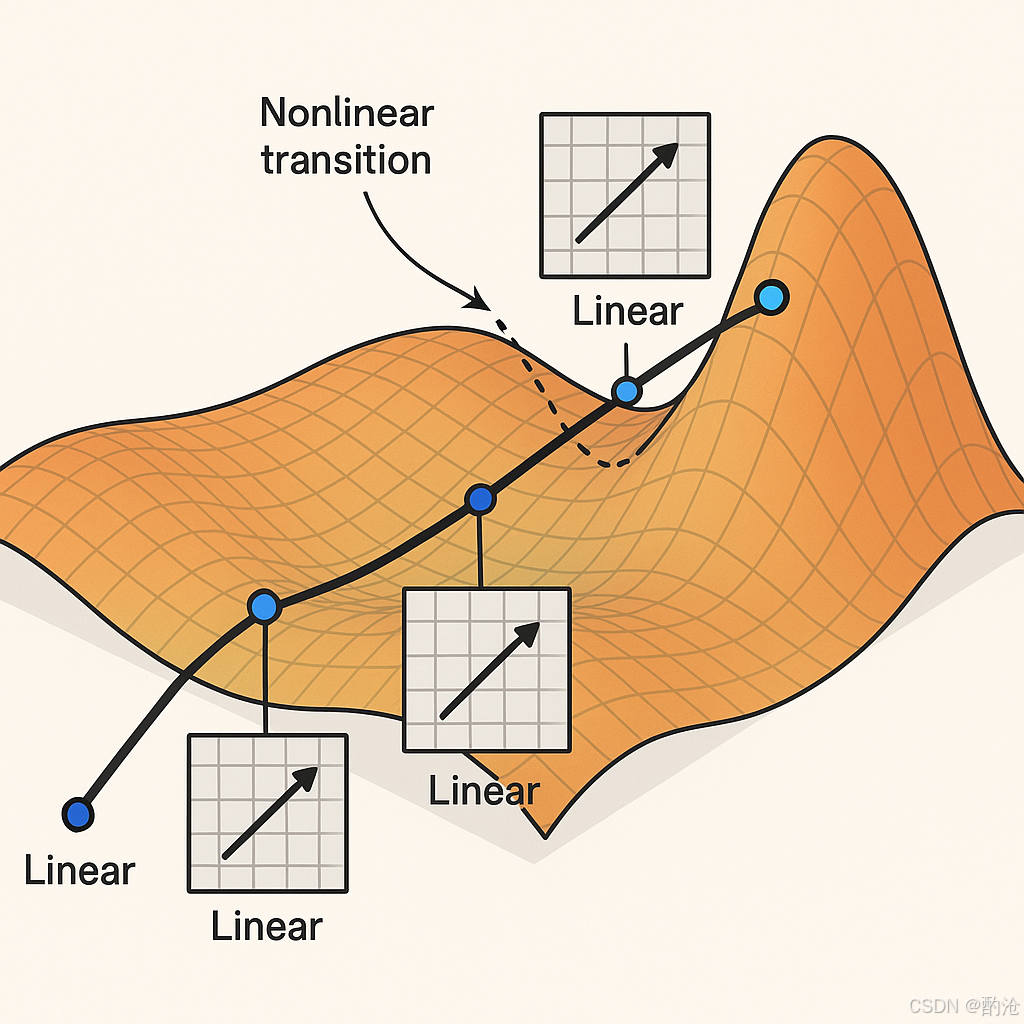
📊 真实世界的数据(图片、语音、文本)分布在在一个像“地毯”一样弯曲的表面上。你从入口出发,沿着地毯走到终点(比如从一张图片走到“猫”这个标签)。你的路线可能经过很多弯曲的部分,每段直线对应着矩阵乘法(线性变换),每个拐弯对应着非线性激活切换。这样一路走下去,你就完成了一次从输入到输出的旅程,这个过程在神经网络里就是推理。
深入思考
如果世界仅由数字构成,我们如何唯一地描述一幅图像、一段语音,或一次梯度更新?答案必须同时满足:可计算、可组合、可度量。这逼迫我们寻找能被算术闭包、向量空间运算、范数度量共同支持的载体:张量。在线性代数中,向量与矩阵便是这种载体的最简形态。深度学习把世界的结构落在三件事上:可计算(能被有限步算子执行)、可组合(小模块可堆叠)、可度量(相似/距离可定义)。能同时满足三者并与现代硬件高效耦合的,正是向量空间与线性映射。
📊 如果世界仅由数字构成,我们如何唯一地描述一幅图像、一段语音,或一次梯度更新?答案必须同时满足:可计算、可组合、可度量。这逼迫我们寻找能被算术闭包、向量空间运算、范数度量共同支持的载体:张量。深度学习把世界的结构落在三件事上:可计算(能被有限步算子执行)、可组合(小模块可堆叠)、可度量(相似/距离可定义)
2 基础元素-标量
标量:度量世界的起点,只含大小
标量是一维空间中的基本元素,只拥有大小而无方向。例如温度、学习率等均是标量。
- 记号:普通小写 xxx,定义域 x∈Rx \in \mathbb{R}x∈R
- 代码示例:
torch.tensor(3.0)
标量在深度学习中通常用作超参数或单一输出(如分类概率),为更高阶的数据表示提供度量基准。
3 基础元素-向量
向量:信息的紧凑表达,有方向与幅值
向量通过有序的标量集合形成,拥有大小与方向,能高效地描述多维状态。
- 记号:粗体小写 x,维度为 nnn,即 x ∈ ℝⁿ
- 实践用途:用户画像、一帧心电图、词嵌入等
- 代码示例:
torch.arange(4)→tensor([0,1,2,3])
向量通过维度的长度直观表示信息量,成为深度学习模型输入特征的基本单位。
4 基础元素-矩阵
矩阵:批量运算的万能载体,向量的有序集合
矩阵是一组向量的集合,以二维表格形式表达数据。
-
记号:粗体大写 A ∈ ℝ^{m×n},其中行代表样本,列代表特征。
-
常用操作:转置 ATA^TAT、索引 A[i,j]A[i,j]A[i,j]、对称性检查 A=ATA = A^TA=AT
-
代码示例:权重矩阵的批量处理
矩阵实现了数据批量处理,让深度学习模型高效利用 GPU 并行计算能力。
5 基础元素-张量
张量:多维数据的统一表达
张量是矩阵概念的自然延伸,能表示任意维度的数据结构。
- 举例:3D 图像 (C,H,W),视频 (T,C,H,W)
- 代码示例:
torch.arange(24).reshape(2,3,4)
张量在深度学习框架中具有一等地位,支持广播、切片、视图变换等操作,让数据与算法自然融合。
6 核心运算-Hadamard积
Hadamard 积:特征的高效交互
Hadamard 积指两个同形状张量逐元素相乘,捕捉特征间的局部交互。
- 记号:A⊙BA \odot BA⊙B
- GPU 并行高效实现:
A * B - 实践示例:在推荐系统中,用户向量与物品向量逐元素相乘,以快速捕捉用户偏好。
7 核心运算-降维
降维:聚焦重要信息
降维技术通过沿某一轴汇总(如求和或平均)来减少数据冗余,突出关键信息。
- 常见操作:
A.sum(axis=0)、mean、cumsum - 实践示例:卷积神经网络中的全局平均池化,压缩图像特征。
8 核心运算-点积
点积:相似度度量之基石
向量点积通过累加逐元素乘积来量化向量间的相似性。
- 公式:x⋅y=∑xiyix \cdot y = \sum x_i y_ix⋅y=∑xiyi
- 应用实例:注意力机制、Word2Vec、余弦相似度
- 代码示例:
torch.dot(x,y) - 实践示例:在搜索引擎中,利用余弦相似度衡量文档与查询词的相关性。
9 核心运算-矩阵向量乘法
矩阵-向量乘法:快速线性变换
矩阵-向量乘积(Ax)实现了高效的线性变换。
- 代码示例:
torch.mv(A,x) - 实践示例:神经网络全连接层将输入特征映射到隐藏层。
10 核心运算-矩阵矩阵乘法
矩阵-矩阵乘法:批量线性映射
矩阵-矩阵乘法(AB)可视作一系列矩阵-向量乘法的集合。
- 形状要求:A(n×k)⋅B(k×m)=C(n×m)A(n \times k) \cdot B(k \times m) = C(n \times m)A(n×k)⋅B(k×m)=C(n×m)
- 代码示例:
torch.mm(A,B) - 实践示例:Transformer 模型中多头注意力机制的批量计算。
11 核心运算-高维张量运算
在实际神经网络中,我们往往需要对多个矩阵进行批量乘法,例如:
A = torch.randn(3, 3, 2) # 3个[3x2]矩阵
B = torch.randn(3, 2, 4) # 3个[2x4]矩阵
C = torch.matmul(A, B) # -> C.shape = [3, 3, 4]
每组进行 [3,2] × [2,4] 的矩阵乘法,最终得到 3 个 [3,4] 的矩阵,结果为 [3, 3, 4]。
仅最后两维按矩阵乘法计算:[…, m, k] @ […, k, n] -> […, m, n]。其余前缀维度 广播对齐。
12 广播机制
从右向左对齐维度,两个维度相等,或其中一个为 1,才允许广播。常见广播是用于加偏置(行向量/列向量)。
a = torch.empty(3, 3, 2)
b = torch.empty(2, 4)
result = a @ b # 自动广播为 [3, 3, 4]
a.shape = [3, 3, 2]b.shape = [2, 4]→ 自动变成[1, 2, 4]→ 广播成[3, 2, 4]- 执行
[3,3,2] @ [3,2,4] = [3,3,4]
13 核心运算-范数
范数:度量数据差异的标尺
范数为向量提供了量身定制的度量工具,直观表示向量的大小和稀疏性。
-
L2 范数 ∥x∥2\|x\|_2∥x∥2:欧式距离与正则化。
-
L1 范数 ∥x∥1\|x\|_1∥x∥1:强调稀疏性,对异常数据更鲁棒。
-
实践示例:L2 正则化在神经网络训练中防止过拟合。
综上,线性代数以向量、矩阵、张量等核心概念为工具,深刻且全面地支撑了深度学习从数据表达到模型训练的全过程,成为了所有AI技术发展的根本语言与方法论。
