【arXiv2025】计算机视觉|FGA:即插即用!让你的模型精准预测人群密度!

论文地址:https://arxiv.org/pdf/2407.06110 代码地址:https://github.com/AIRLABkhu/FGA3
关注UP CV缝合怪,分享最计算机视觉新即插即用模块,并提供配套的论文资料与代码。 CV缝合怪的个人空间-CV缝合怪个人主页-哔哩哔哩视频
摘要
本研究提出了傅里叶引导注意力(FGA),一种用于人群计数估计的新型注意力机制,旨在解决现有基于卷积的注意力网络中全尺度全局模式捕获效率低下的问题。FGA 通过利用快速傅里叶变换 (FFT) 以及针对全局特征的空间注意力和针对半全局和局部特征的通道注意力卷积来有效地捕获多尺度信息,包括全尺度全局模式。FGA 的架构涉及双路径方法:(1)通过 FFT 处理全尺度全局特征的路径,从而有效提取频域信息;(2)使用传统卷积和通道注意力处理剩余特征图以获取半全局和局部特征的路径。这种双路径架构使 FGA 能够无缝集成频率和空间信息,增强其捕获各种人群模式的能力。本研究将 FGA 应用于两个流行的人群计数工作 CSRNet 和 CANNet 的最后一层,以评估该模块在 ShanghaiTech-A、ShanghaiTech-B、UCF-CC-50 和 JHU++ crowd 等基准数据集上的性能。实验表明,基于均方误差 (MSE) 和平均绝对误差 (MAE) 指标,所有数据集都有显着改进,与最新的方法相比表现出相当的性能。此外,本研究使用 Grad-CAM 热图进行定性分析来说明其可解释性,以展示 FGA 在捕获人群模式方面的有效性。
引言
本研究关注人群计数估计领域,旨在解决现有基于卷积注意力网络的全局模式捕获效率低下的问题。人群计数估计在公共安全、人群管理、城市规划和医疗保健等领域具有重要意义。由于大范围的前景-背景失衡、遮挡和透视变形等问题,在大型人群场景中进行人群计数变得极具挑战性。目前,基于密度图的人群计数方法被广泛接受,该方法通过预测人群密度图,并对密度图中的像素值求和来估计人群数量。
深度学习的引入显著推进了人群计数领域的发展,涌现出许多基于CNN的密度图回归方法。然而,这些方法仍然受限于卷积核的感受野,导致无法有效地捕获模型中的全局或长程模式。在人群计数中,全局感受野允许网络捕获更广泛上下文的信息,确保其考虑人群的整体布局,并考虑人群密度分布的变化。许多基于注意力的研究,例如MAN、DMCNet、JANet和DA2Net,由于其能够通过注意力网络理解大规模依赖关系而受到欢迎。例如,BBA-net提出了一种基于注意力的网络,旨在捕获空间位置的细粒度细节;RFSNet则引入了一种用于视频时空人群计数的逐块循环自注意力网络。
尽管这些基于CNN的方法表现出色,但它们仅利用能够在局部邻域内处理信息的卷积,忽略了大规模像素间的上下文;因此,单独使用卷积层对于理解全尺度全局模式来说效率低下。为解决这个问题,本研究提出了一种名为傅里叶引导注意力(FGA)模块的新型神经网络架构,其灵感来自快速傅里叶卷积(FFC)。该模块专为远程上下文感知人群计数而设计,将FFC、空间注意力和通道注意力无缝地结合到一个单元中。FFC在空间域和频域中运行,使FGA能够同时处理局部和全局感受野的信息。同时,不同的注意力机制专注于放大来自输入序列不同部分的细粒度特征,以捕获相关信息。所提出的框架可以集成到现有的人群计数方法中,以关注全尺度全局特征。
论文创新点
✨ 傅里叶引导注意力 (FGA) 用于人群计数估计 ✨
本研究提出了一种名为 傅里叶引导注意力(FGA) 的新型注意力机制,用于人群计数估计,旨在解决现有基于卷积的注意力网络在全尺度全局模式捕获方面的低效性。
1. 🚀 FGA 的核心思想 🚀
-
利用快速傅里叶变换 (FFT) 以及空间注意力来处理全局特征,并使用带有通道注意力机制的卷积来处理半全局和局部特征,从而有效地捕获多尺度信息,包括全尺度全局模式。
2. 🚄 FGA 的双路径架构 🚄
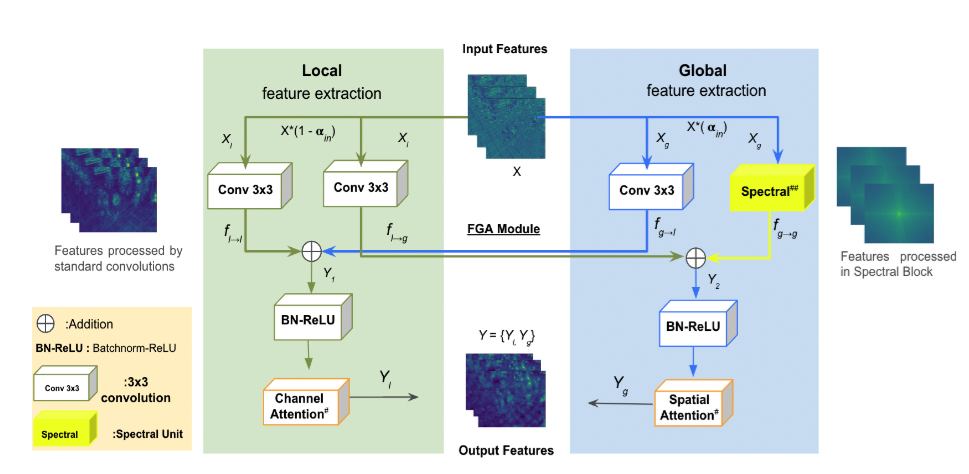
本研究的FGA架构采用双路径方法:
-
(1) 全局特征路径: 通过 FFT 处理全尺度全局特征,允许在频域中高效提取信息。
-
(2) 半全局和局部特征路径: 使用传统卷积和通道注意力处理剩余特征图以获取半全局和局部特征。
这种双路径架构使 FGA 能够无缝集成频率和空间信息,增强其捕获各种人群模式的能力。
3. 📊 实验结果与数据集 📊
-
将 FGA 应用于两个流行的人群计数工作 CSRNet 和 CANNet 的最后一层。
-
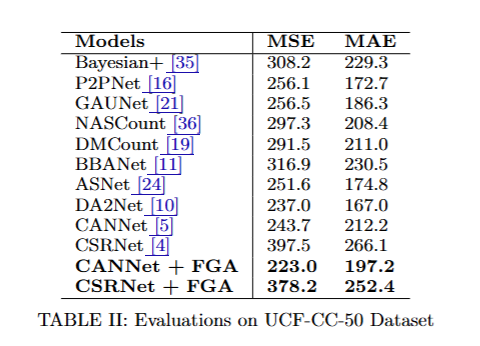
在 ShanghaiTech-A、ShanghaiTech-B、UCF-CC-50 和 JHU++ crowd 等基准数据集上评估性能。
-
基于均方误差 (MSE) 和平均绝对误差 (MAE) 指标,所有数据集都有显著改进,其性能与最新的方法相当。
4. 🔍 可解释性与消融实验 🔍
-
利用 Grad-CAM 热力图 进行定性分析,以说明 FGA 在捕获人群模式方面的有效性,从而增强了模型的可解释性。
-
消融实验验证了FGA模块中每个组成部分(FFT、空间注意力和通道注意力)的有效性以及它们对整体性能的贡献。
5. 📈 不同人群密度下的性能分析 📈
-
分析了在不同人群密度下的计数样本,结果表明,该模型在低密度、中等密度和高密度人群中均表现出色。
-
观察到在高密度人群中性能略有下降,这需要进一步分析傅里叶引导注意力在高人群密度下略微下降的原因,并将其作为该领域未来的研究方向。
论文实验