基于径向基函数神经网络的数据回归预测 RBF
一、作品详细简介
1.1附件文件夹程序代码截图

全部完整源代码,请在个人首页置顶文章查看:
学行库小秘_CSDN博客编辑https://blog.csdn.net/weixin_47760707?spm=1000.2115.3001.5343
1.2各文件夹说明
1.2.1 main.m主函数文件
以下是该MATLAB代码的详细实现步骤解析,该代码实现了一个基于RBF径向基函数神经网络的数据回归预测模型,模型按执行顺序分为核心模块:
1. 数据导入与预处理
- 功能:加载名为数据集.xlsx的Excel文件
- 数据结构:假设数据包含103行(样本)和8列(前7列为特征,第8列为目标值)
2. 训练集/测试集划分
关键操作:
- randperm(103):随机打乱样本顺序(避免有序数据影响)
- 80/23分割:约77.7%训练集 + 22.3%测试集
- 转置操作 ':将行样本转为列向量(符合神经网络输入格式)
3. 数据归一化
- 归一化原理:
- 对每个特征独立归一化:$X_{\text{norm}} = \frac{X - X_{\min}}{X_{\max} - X_{\min}}$
- ps_input/ps_output:保存训练集的归一化参数(避免数据泄露)
- 目的:消除量纲影响,提升神经网络训练稳定性
4. RBF神经网络创建
- 网络类型:精确径向基网络(Exact RBF)
- 核心参数:
- rbf_spread:控制径向基函数的宽度(越大函数越平滑)
- 隐含层神经元数 = 训练样本数(80个),无需手动设置
- 特点:单次计算完成训练(无需迭代),零训练误差
5. 预测与反归一化
- sim()函数:使用训练好的网络进行预测
- 反归一化:将预测值转换回原始物理量纲
6. 性能评估
均方根误差 (RMSE)
- 公式:$\text{RMSE} = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}$
决定系数 (R²)
- 值域[0,1],越接近1说明拟合效果越好
平均绝对误差 (MAE)
- 公式:$\text{MAE} = \frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y}_i|$
平均偏差误差 (MBE)
- 反映预测值系统性偏高/偏低(正值表示高估,负值表示低估)
7. 结果可视化
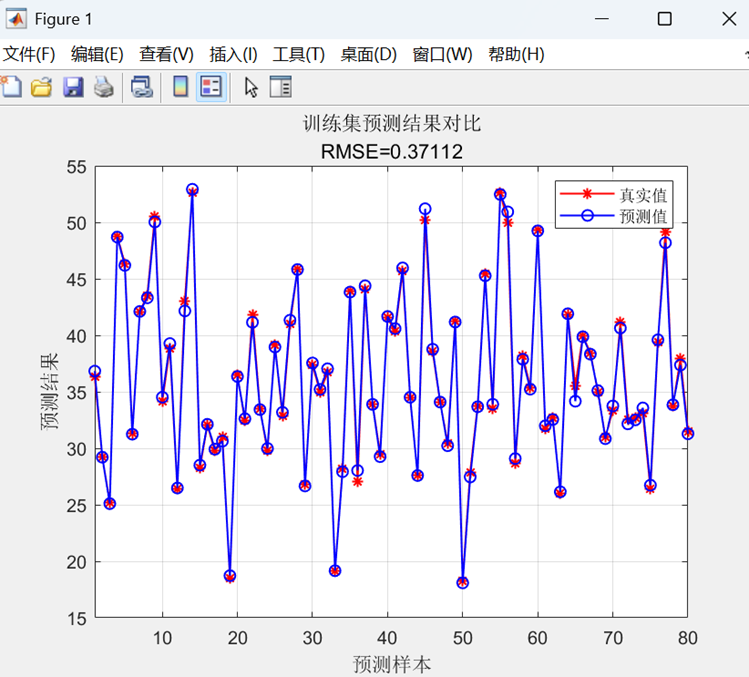
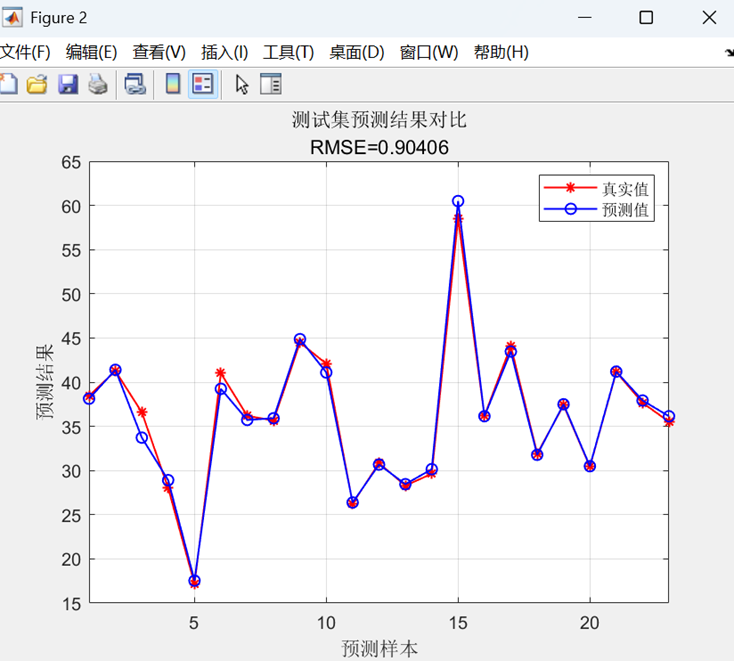
预测对比图
- 红色*:真实值,蓝色o:预测值
- 标题包含RMSE值
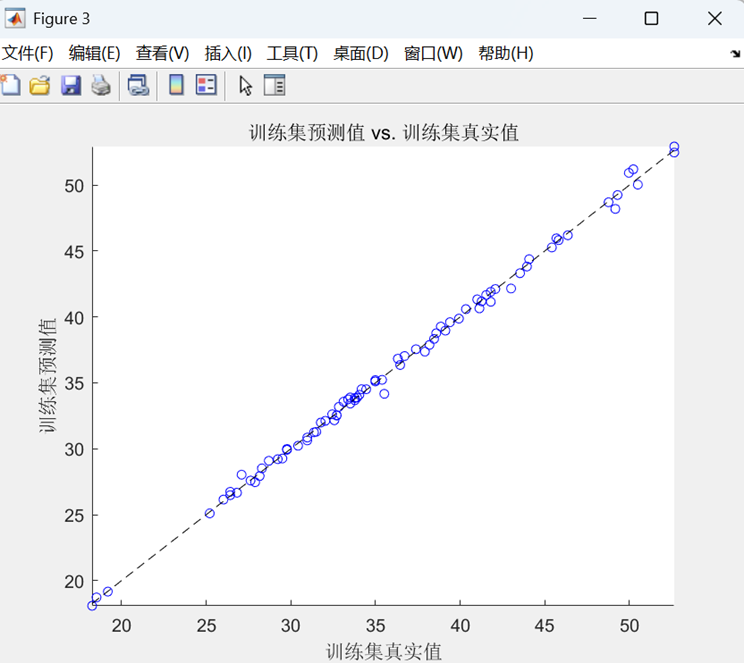
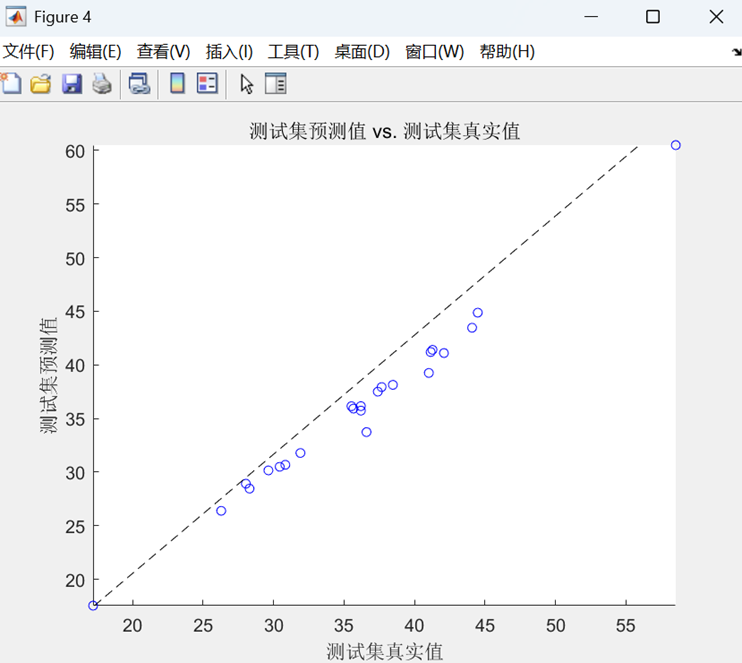
散点拟合图
- 数据点越接近黑色虚线,预测越准确
网络结构查看
- 可视化展示RBF网络的输入层、径向基层、输出层结构
关键技术总结
- 数据分割:随机排列避免顺序偏差
- 归一化处理:使用训练集参数统一处理测试集
- RBF网络特性:
- 隐含层神经元数=训练样本数
- 扩展参数spread影响函数平滑度
- 零训练误差设计(精确插值)
- 多维度评估:RMSE/R²/MAE/MBE全面衡量性能
- 可视化诊断:误差曲线+散点图直观判断拟合质量
注意事项:RBF网络在训练集上必然达到零误差,需重点关注测试集性能(error2, R2等指标)以避免过拟合。扩展参数spread=100可能需要根据实际数据调整优化。
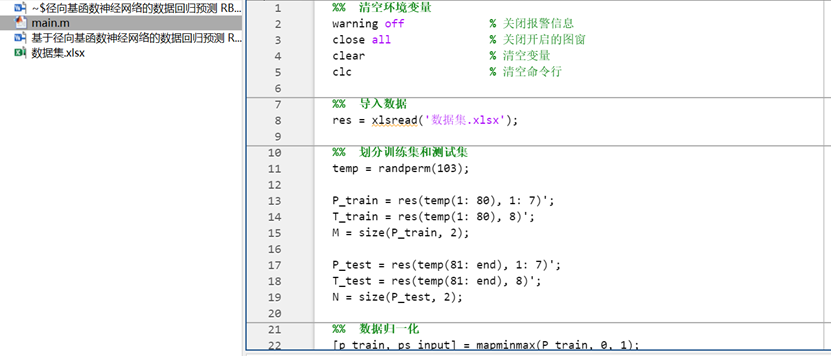
图2 main.m主函数文件部分代码
1.2.2 数据集文件
数据集为Excel数据csv格式文件,可以方便地直接替换为自己的数据运行程序。原始数据文件包含7列特征列数据和1列输出标签列数据,一共包含103条样本数据,具体如图所示。
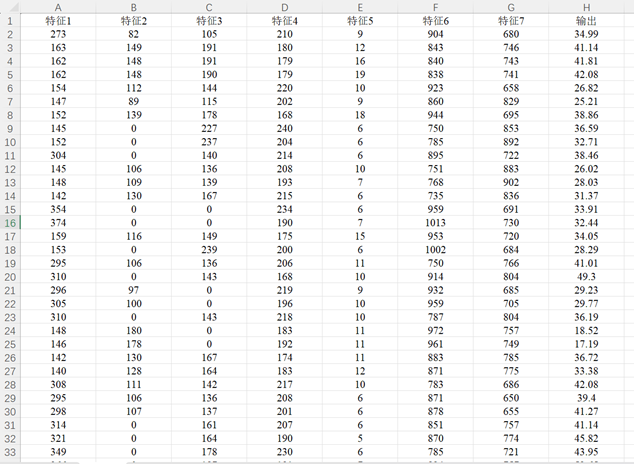
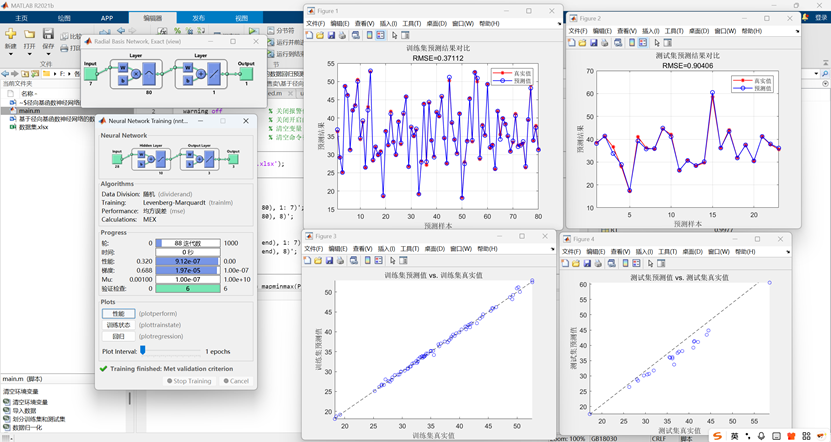
二、代码运行结果展示
该MATLAB代码实现了一个基于RBF神经网络的回归预测模型。
首先,代码导入Excel数据集,随机划分80个样本作为训练集、23个样本作为测试集,并对特征和目标值进行归一化处理;
其次,创建精确径向基网络(newrbe)进行训练和预测,将结果反归一化后恢复原始量纲;
最后,通过计算RMSE、R²、MAE和MBE多指标评估性能,并绘制预测对比曲线、散点拟合图及网络结构图进行可视化分析。
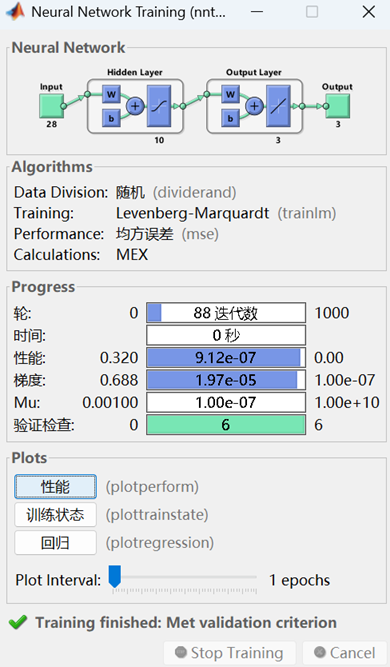
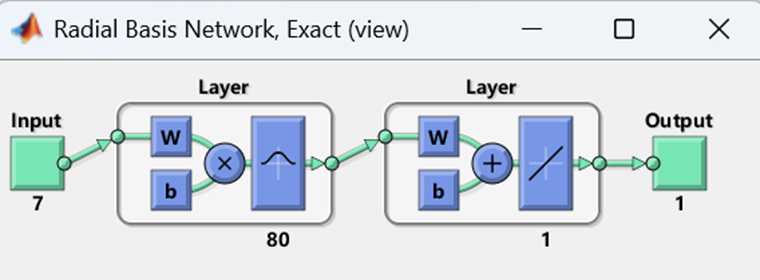
三、注意事项:
1.程序运行软件推荐Matlab 2018B版本及以上;
2.所有程序都经过验证,保证程序可以运行。此外程序包含简要注释,便于理解。
3.如果不会运行,可以帮忙远程运行原始程序以及讲解和其它售后,该服务需另行付费。
4. 代码包含详细的文件说明,以及对每个程序文件的功能注释,说明详细清楚。
5.Excel数据,可直接修改数据,替换数据后直接运行即可。
