LintCode第137-克隆图
描述
克隆一张无向图. 无向图的每个节点包含一个 label 和一个列表 neighbors. 保证每个节点的 label 互不相同.
你的程序需要返回一个经过深度拷贝的新图. 新图和原图具有同样的结构, 并且对新图的任何改动不会对原图造成任何影响
你需要返回与给定节点具有相同 label 的那个节点
样例1
输入:
{1,2,4#2,1,4#4,1,2}
输出:
{1,2,4#2,1,4#4,1,2}
解释:
1------2 \ | \ | \ | \ | 4
节点之间使用 '#' 分隔
1,2,4 表示某个节点 label = 1, neighbors = [2,4]
2,1,4 表示某个节点 label = 2, neighbors = [1,4]
4,1,2 表示某个节点 label = 4, neighbors = [1,2]/**
* Definition for Undirected graph.
* class UndirectedGraphNode {
* int label;
* List<UndirectedGraphNode> neighbors;
* UndirectedGraphNode(int x) {
* label = x;
* neighbors = new ArrayList<UndirectedGraphNode>();
* }
* }
*/
思路:该题的数据结构是考察邻接表的深度拷贝
那么问题来了 什么是邻接表的浅拷贝和深度拷贝
拷贝时只复制引用,不新建对象。
结果是新表和原表共享内部数据,修改一个会影响另一个
eg:
UndirectedGraphNode copy = new UndirectedGraphNode(node.label);
copy.neighbors = node.neighbors; // 浅拷贝
再看看看邻接表的深拷贝
拷贝时不仅复制外层,还要为内层对象重新 new,并递归复制它们的内容
eg:
List<List<Integer>> deep = new ArrayList<>();
for (List<Integer> neighbors : adj) {
deep.add(new ArrayList<>(neighbors)); // 每个内层 List 都重新建
}
搞清楚了 邻接表的浅拷贝和深拷贝的区别 我们就可以分析该题的思路和易错点
通常情况下 无向图的连接 我们首先要想到环问题即无向图的结构有可能出现环 不像树结构 如何禁止遍历环 造成死循环呢 第一种:建立visited访问数组 访问一个将其默认值从false变为true 第二种使用天然防止重复的数据结构 防止重复访问 即map或者Set集合
又由于需要考虑到防止克隆时复建多个不同的对象 结构被破坏 即第一次新建对象的时候new 对象 然后存入map 如果下次又访问到相同的对象那么就get(key)来获取之前new出来的对象 为什么下次又会访问到 因为是无向图 无向图以 A B C三点为例 既可以从A - C 可以C -A 所以各点都有重复访问的可能性 但不能每次访问的时候都新加边 这样会破坏原对象的结果
举例:
A 的两个邻居都指向 B
期望:A' 的两个邻居都应指向同一个 B'
若无 map:你会建 B'1、B'2 两个不同对象,错了
由于map即有防止死循环的功能 又有防止重复克隆的能力 所以使用map作为映射
考虑的既要防止重复访问 又要防止重复克隆对象 那么map是最方便的数据结构 而且map会记录边的信息
即副本对象(clone 出来的节点)其实不是“整体复制内存”,而是一步步 new + 填充字段
克隆过程(用 BFS 举例)
Step 1: 起点 A
map.put(A, new UndirectedGraphNode(A.label))
得到 A′(副本):

队列里放入 A
Step 2: 处理 A
从队列取出 A,找到副本 A′。
遍历 A 的邻居:
遇到 B:map 里没有 →
new B′,map.put(B, B′),队列入 B。
然后A′.neighbors.add(B′)遇到 C:map 里没有 →
new C′,map.put(C, C′),队列入 C。
然后A′.neighbors.add(C′)
现在副本图长这样:

Step 3: 处理 B
队列取出 B,找到副本 B′。
遍历 B 的邻居:
邻居 A:map 已有 A → 直接拿 A′ →
B′.neighbors.add(A′)邻居 C:map 已有 C → 拿 C′ →
B′.neighbors.add(C′)
Step 4: 处理 C
队列取出 C,找到副本 C′。遍历 C 的邻居:
邻居 A:map 已有 A → 拿 A′ →
C′.neighbors.add(A′)邻居 B:map 已有 B → 拿 B′ →
C′.neighbors.add(B′)
最终克隆图
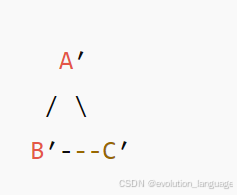
每个原节点 → 唯一副本(靠 map 保证)。
邻居列表一模一样。
核心点:
new 时只拷贝 label。
邻居关系用 map.get() 查副本来补齐。
遇到旧节点时不会重新 new,而是复用已建副本
问题:
以上面A B C三个点为例
实际边数 = 3 条。
邻接表里记录 = 6 次(双向)
克隆时也会复制 6 次
虽然是3条边 但是有6次记录 是邻接表的正确表示
邻接表表示法中,无向边 = 两个方向各存一份
map.containsKey(node) 理解为两层含义:
访问标记:说明这个原节点已经被处理过,不要再递归/入队。
副本索引:说明你可以直接拿到这个原节点对应的副本,用来连边
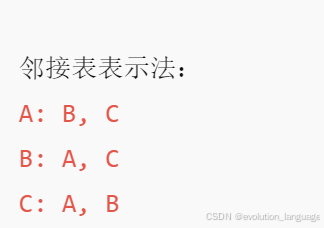
邻接表表示法:
A: B, C
B: A, C
C: A, B
代码如下:
/**
* Definition for Undirected graph.
* class UndirectedGraphNode {
* int label;
* List<UndirectedGraphNode> neighbors;
* UndirectedGraphNode(int x) {
* label = x;
* neighbors = new ArrayList<UndirectedGraphNode>();
* }
* }
*/
public class Solution {
/**
* @param node: A undirected graph node
* @return: A undirected graph node
*/
public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
if(node==null)
{
return null;
}
// old -> new
Map<UndirectedGraphNode, UndirectedGraphNode> map = new HashMap<>();
// 注意:原类没有无参构造,必须带 label
UndirectedGraphNode DeepCopyCloneGraphNode = new UndirectedGraphNode(node.label);
map.put(node, DeepCopyCloneGraphNode);
// 用标准 Java 队列:offer / poll
Queue<UndirectedGraphNode> UndirectedGraphNodeQueue = new ArrayDeque<>();
UndirectedGraphNodeQueue.offer(node);
//取出
while(!UndirectedGraphNodeQueue.isEmpty())
{
UndirectedGraphNode currentUndirectedGraphNode = UndirectedGraphNodeQueue.poll();
UndirectedGraphNode currentCopy = map.get(currentUndirectedGraphNode);
// 遍历原图邻居
for (UndirectedGraphNode neighbor : currentUndirectedGraphNode.neighbors) {
if (!map.containsKey(neighbor)) {
map.put(neighbor, new UndirectedGraphNode(neighbor.label));
UndirectedGraphNodeQueue.offer(neighbor);
}
// 在克隆图中连边:当前拷贝节点 -> 邻居的拷贝
currentCopy.neighbors.add(map.get(neighbor));
}
}
return DeepCopyCloneGraphNode;
}
}
扩展:
邻接表:
如果是邻接矩阵的浅拷贝和深度拷贝呢 上面是邻接表的
同样三角形 A–B–C–A,用矩阵表示(设 A=0, B=1, C=2):
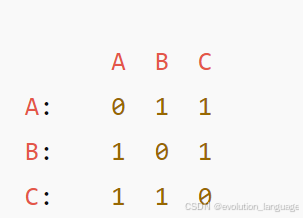
邻接矩阵的浅拷贝:
第一种:int[][] clone = matrix.clone();
第二种:int[][] clone = new int[matrix.length][];
for (int i = 0; i < matrix.length; i++) {
clone[i] = matrix[i]; // 直接引用行
}
邻接矩阵的深度拷贝:
深度拷贝第一种方式:双重 for 循环
int V = matrix.length;
int[][] clone = new int[V][V];
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
clone[i][j] = matrix[i][j];
}
}
深度拷贝第二种方式:System.arraycopy
int V = matrix.length;
int[][] clone = new int[V][V];
for (int i = 0; i < V; i++) {
System.arraycopy(matrix[i], 0, clone[i], 0, V);
}
深度拷贝第三种方式:Arrays.copyOf
int V = matrix.length;
int[][] clone = new int[V][V];
for (int i = 0; i < V; i++) {
clone[i] = Arrays.copyOf(matrix[i], V);
}
总结 邻接矩阵的深度拷贝和浅拷贝的区别是
双 for、System.arraycopy、Arrays.copyOf = 深拷贝
直接 clone() 或行引用赋值 = 浅拷贝
