数据结构之heap算法
文章目录
- 前言
- 1. heap结构概述
- 2. push_heap
- 3. pop_heap
- 4. sort_heap
- 5. make_heap
前言
-
heap这种数据结构,允许用户以任何次序将任何数据放入该结构中,但是最后取出数据的时候一定是权值最高(或者最低)的元素。主要和实现有关,根据比较方法的不同,实现大根堆/小根堆的算法……
下面小编主要是实现大根堆的算法。
-
并且如果一个类型需要进行使用堆来进行存储,那么这个类型一定是支持比较方法的。
本文章就和大家来探讨堆的算法。例如:
- push_heap
- pop_heap
- sort_heap
- make_heap
1. heap结构概述
-
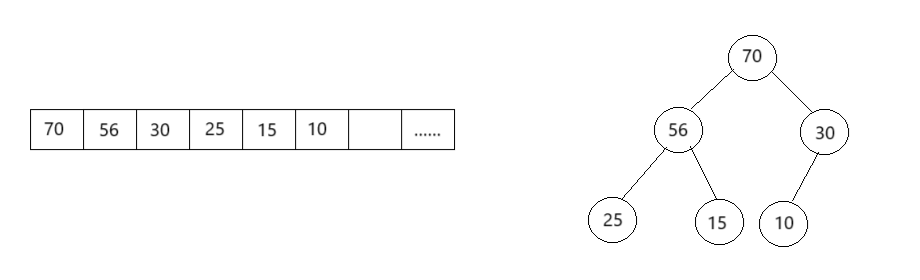
heap的底层就是使用的一个完全二叉树(逻辑上)。我们使用vector/array容器来作为heap的底层结构,再以顺序结构构建这颗完全二叉树(物理存储上)。
-
大根堆:任意一个父节点的权值都大于等于孩子节点的权值。
-
小根堆:任意一个父节点的权值都小于等于孩子节点的权值。

-
构建的方式:
-
我们将这颗二叉树的根设置为数组的
0下标。(还有其它设置方法) -
根节点找孩子节点:
当前节点的下标为
i,左孩子的下标为2 * i + 1;右孩子的下标为:2 * i + 2。合理地找到一个根节点左右孩子节点。 -
孩子节点找根节点:
当前节点的下标为
i,父亲节点的下标为(i - 1)/2。 -
-
现有如图的大根堆结构:
2. push_heap
push_heap操作是在原有的堆基础之上,再在这个完全二叉树的结构中添加的新的元素,一般而言会有如下的几个步骤:
-
将新数据新增到物理结构的最后下标位置,但是逻辑结构上仍然是一个完全二叉树。此时,已经破坏了大根堆/小根堆的性质。
-
需要对当前节点的数据进行调整,使得整个完全二叉树满足大根堆/小跟堆的性质。
此时我们用到的调整算法:Percolate Up(上溯)。向上调整。
如下图:
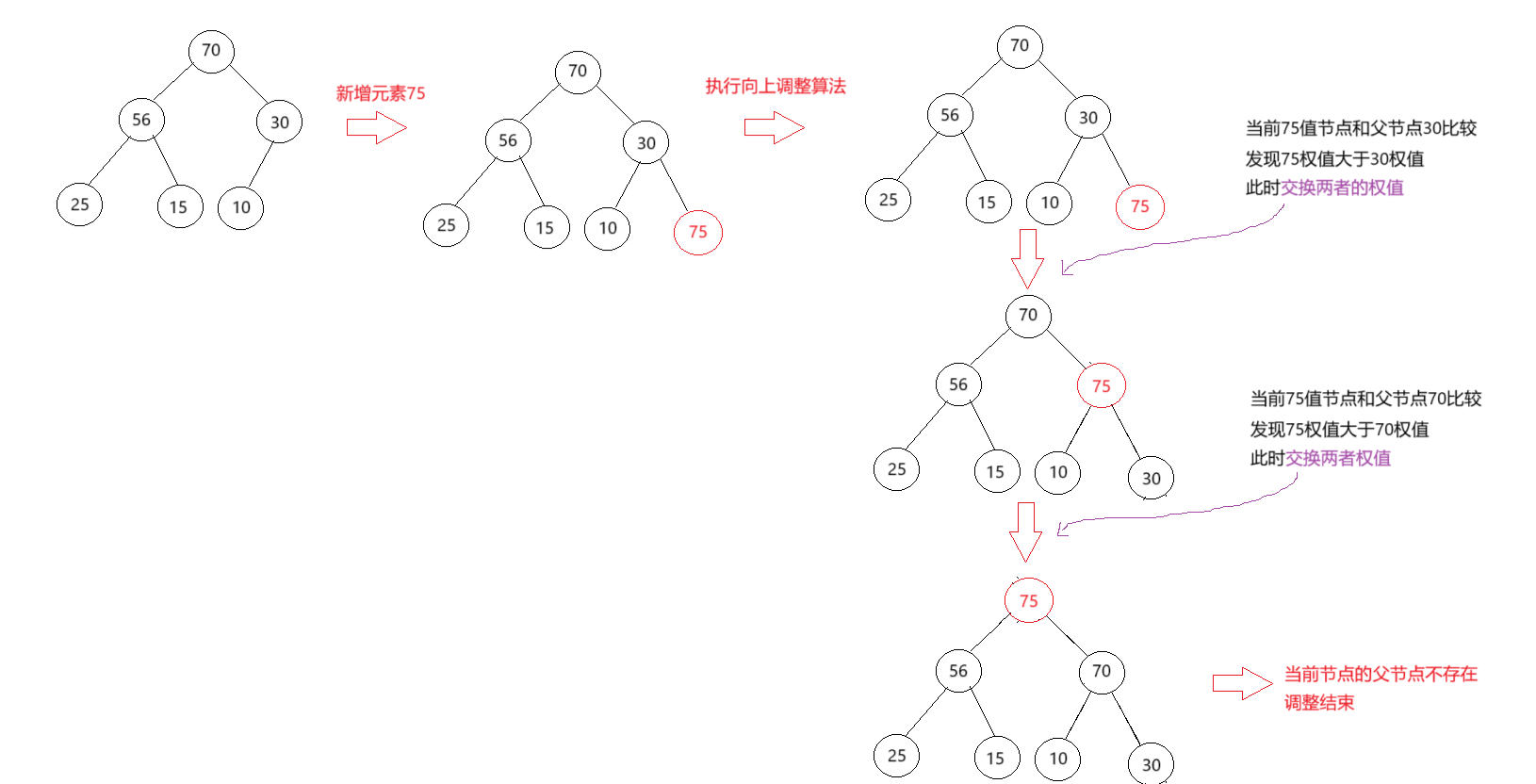
- 调整的结束:当前节点权值小于等于父节点权值或者已经更新到根节点。
void push_heap(int val){_heap.push_back(val); //添加新元素AdjustUp(_heap.size() - 1);}void AdjustUp(size_t child){int index = (int)child; //拿到最后一个位置的下标while (index > 0) //当前调整的节点位置大于0,就继续调整{int parent = (index - 1) / 2; //找到父节点位置if (_heap[parent] < _heap[index]) //父亲节点的key < 当前节点位置的key{//交换两者的权值std::swap(_heap[parent], _heap[index]);}else // >={break;}//调整当前位置的下标index = parent;}}
3. pop_heap
一般来说,pop的操作是取走整个heap的权值最大/最小的节点。根据前面的经验,那么就是需要将根节点的数据取走。根节点在vector中的下标为0。我们该如何取取走该根节点呢?
-
为了满足堆的完全二叉树的性质,所以pop节点一定是最后一个位置的。那么我们能想到的方案就是:
-
交换根节点权值和最后一个节点的权值,执行
pop_back。此时整个heap结构仍然保持完全二叉树结构。但是不满足大根堆/小根堆性质。 -
我们需要对根节点开始调整,使其满足堆的性质。
从根节点开始,执行 Percolate Down(下溯)。向下调整。
-
如下图:
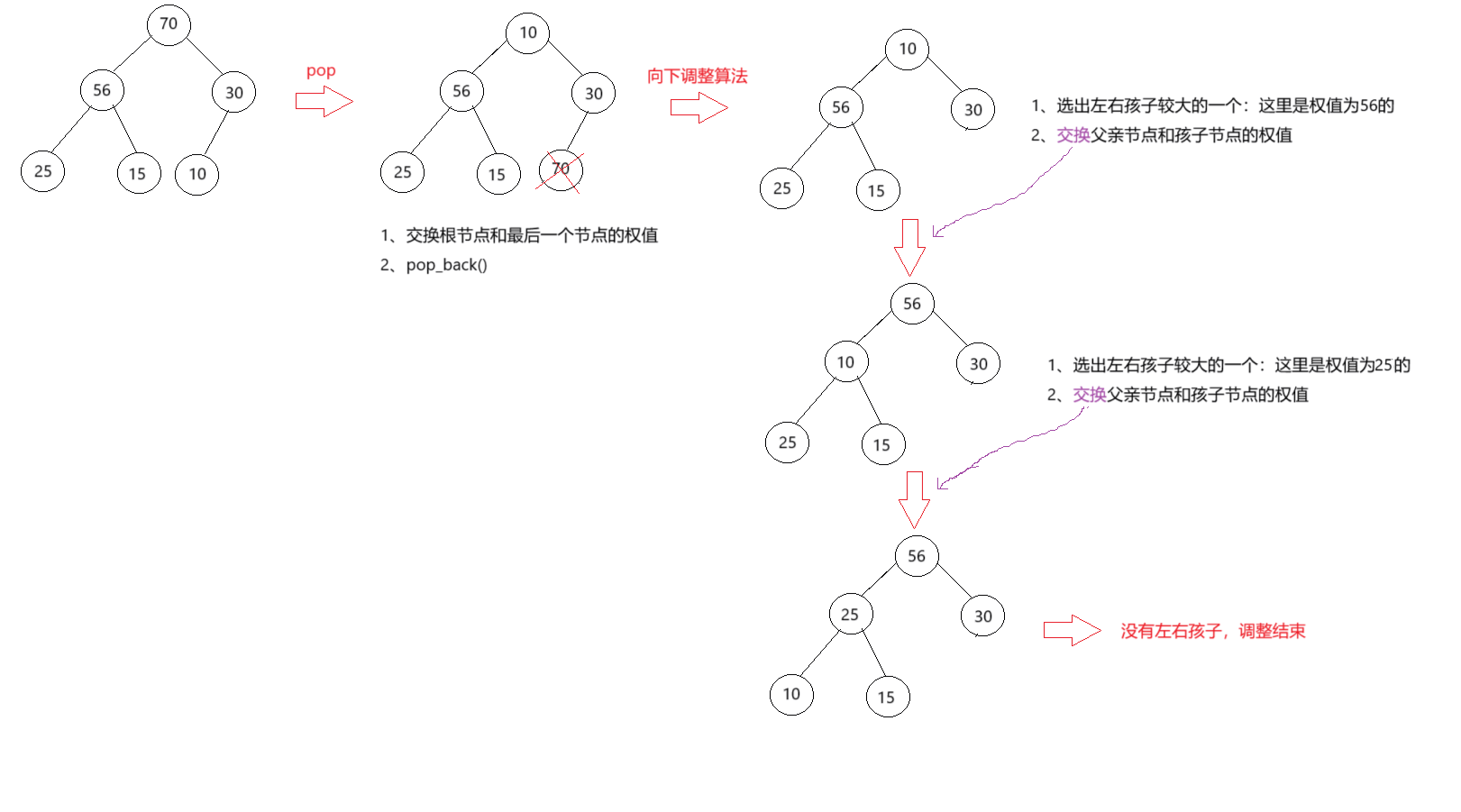
- 调整的结束:当前节点权值小于左右孩子最大节点值或者没有左右孩子。
void pop_heap()
{size_t index = _heap.size() - 1;std::swap(_heap[0], _heap[index]); //交换权值_heap.pop_back(); //删除最后一个元素AdjustDown(0, _heap.size() - 1); //传入根节点的下标和当前heap的有效长度
}void AdjustDown(int index, int size)
{//在完全二叉树中,左孩子存在,但是右孩子不一定存在int child = index * 2 + 1; //假设左孩子大while (child < size) //选取的孩子不能越界;越界了说明孩子不存在{if (child + 1 < size && _heap[child] < _heap[child + 1]){child = child + 1; //更新左右孩子中值较大的}if (_heap[index] < _heap[child]) //父亲比孩子小{std::swap(_heap[index], _heap[child]); //交换权值//继续向下调整}else // >={break;}//更新index和childindex = child;child = 2 * index + 1;}
}
后面的sort_heap会解释,为什么向下调整还需要一个size的参数
4. sort_heap
-
堆排序的思想:
利用堆的性质:每次都能获得当前heap中键值最大的元素。结合pop_heap算法我们可以可以持续对堆中的元素做pop_heap操作。(注意:这里的pop_heap不会将原有的数据删除,而是有效数据的位置减少,在pop_heap中的size参数,就是体现有效数据的地方)这样我们每次都能将键值最大/最小的元素安置在容器的末尾,从而完成升序或者降序……
注意:使用完堆排序之后,这个heap就不再是一个heap了
void sort_heap()
{int size = (int)_heap.size(); //得到当前大小while (size > 1) //剩余元素超过两个{// 模拟pop_backint index = size - 1;std::swap(_heap[0], _heap[index]);--size; //有效长度-1//向下调整AdjustDown(0, size); //向下调整有效长度}
}
5. make_heap
-
建堆一般是根据一个已有的容器/迭代器中的数据,将这些数据构建出一个大根堆/小根堆的算法。很容易我们可以想到一种方法:
方案一:依次将迭代器区间中的元素push_heap到一个新的堆中。
但是这样的建堆方式是利用了向上调整的算法。这个算法要求,除了最后一个位置之外的所有位置,都满足堆结构。后面会进行时间复杂度的分析。
-
如果你比较敏锐,你会发现我们向下调整的算法,要求:当前节点的左右子树必须满足堆结构。
方案二:我们可以局部看待任何一个二叉树,分为左子树 根 右子树。为了实现向下调整的算法。我们似乎的处理方式是:先将左右子树建堆,最后根向下调整。以任何一个。这样的建堆方式如下图:
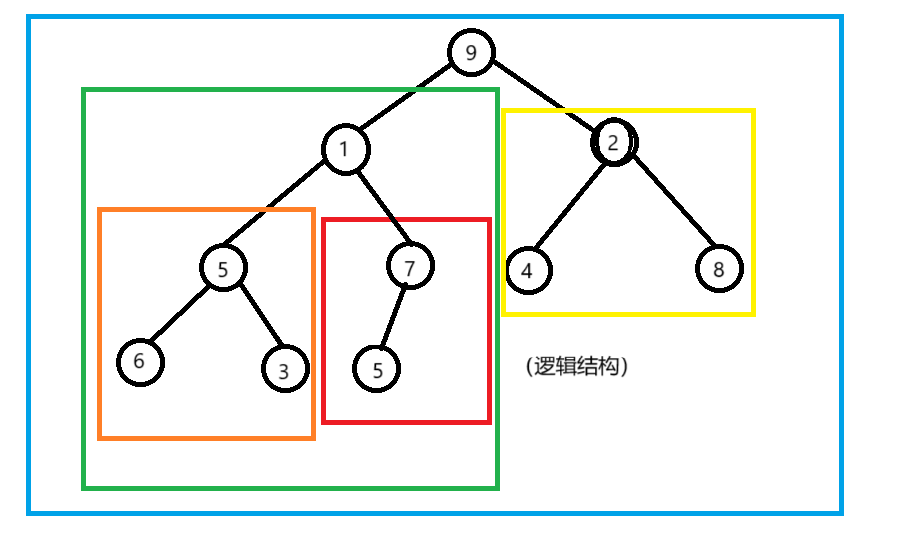
我们采用迭代的方式进行建堆,即:找到没有成堆的最小树开始向下调整。
void make_heap()
{int index = (int)_heap.size() - 1, size = (int)_heap.size(); //堆数据的大小int parent = (index - 1) / 2; //找到父亲节点while (parent >= 0) //实际上调整的节点是父亲节点{AdjustDown(parent, size);--parent; //遍历下一个父亲节点}
}
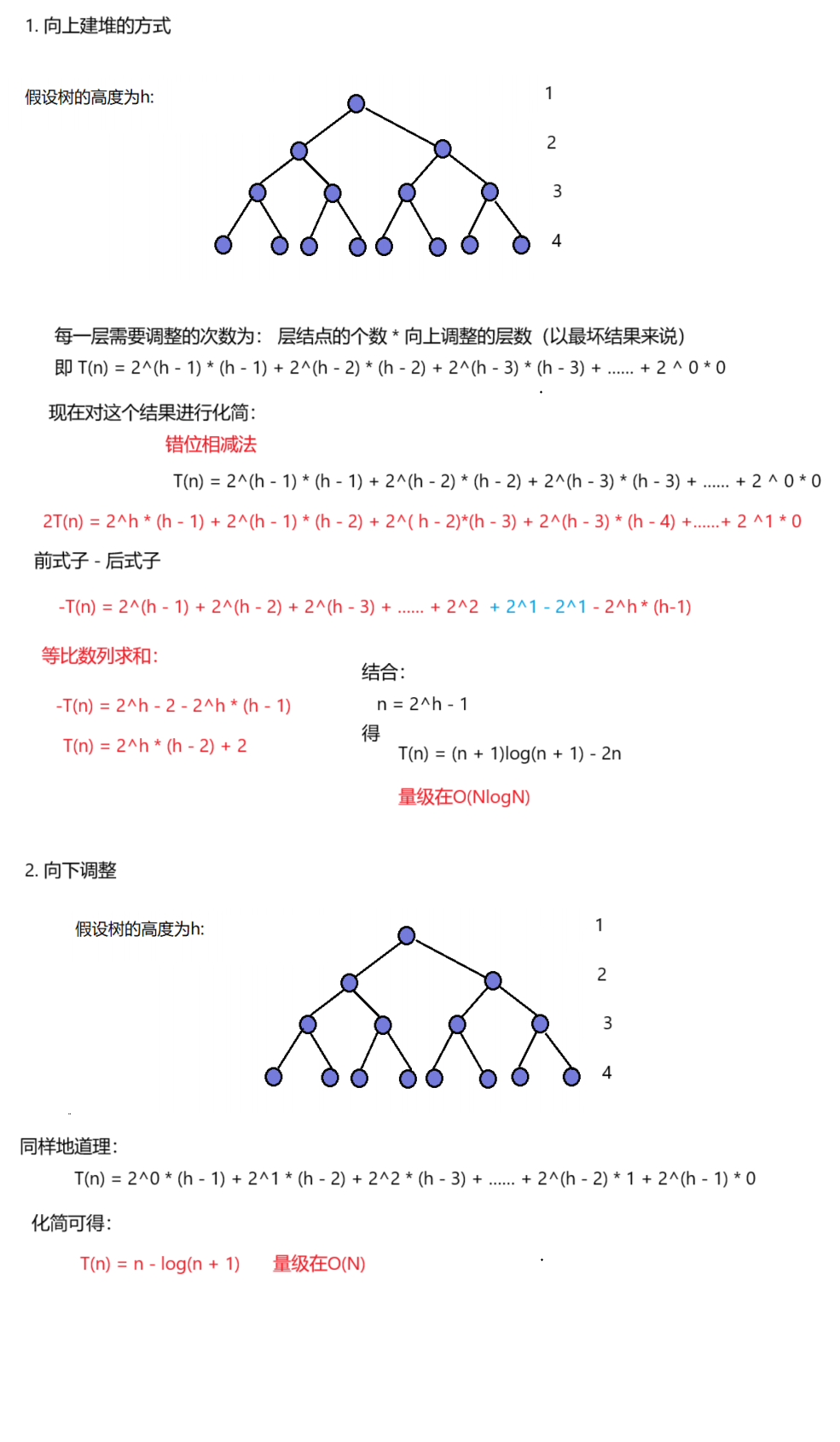
- 时间复杂度分析:
完。
