KNN 算法详解:从电影分类到鸢尾花识别的实战指南
在机器学习领域,K 近邻(KNN)算法以其简单直观的特点成为入门必学的经典算法。从生活案例出发,详解 KNN 原理、距离度量及实战应用,帮你快速掌握这一 "懒学习" 算法的核心逻辑。
一、从电影分类看 KNN:直观理解 "近朱者赤"
KNN 的核心思想可以用 "近朱者赤,近墨者黑" 概括 —— 通过样本的 "邻居" 来判断其类别。PPT 中用电影分类的例子生动诠释了这一点:
| 电影名称 | 打斗镜头数 | 接吻镜头数 | 类型 |
|---|---|---|---|
| California Man | 3 | 104 | 爱情片 |
| He's Not Really into Dudes | 2 | 100 | 爱情片 |
| Beautiful Woman | 10 | 81 | 爱情片 |
| Kevin Longblade | 101 | 5 | 动作片 |
| Robo Slayer 3000 | 99 | 2 | 动作片 |
| Amped II | 98 | 2 | 动作片 |
| 未知电影 | 18 | 90 | ? |
观察可知:爱情片的接吻镜头多、打斗镜头少;动作片则相反。对于 "未知电影"(18 次打斗,90 次接吻),只需找到与其最相似的几部电影(计算距离),看这些电影多属于哪类,即可判断其类型 —— 这就是 KNN 的核心逻辑。
二、KNN 算法原理:四步走的 "懒人逻辑"
KNN 被称为 "懒学习" 算法,因为它不主动构建模型,而是通过存储样本、实时计算距离来预测。其步骤可总结为:
算距离:计算新数据与样本集中所有数据的距离(如欧式距离、曼哈顿距离);
排顺序:按距离从小到大排序;
选邻居:选取距离最近的 k 个样本(k 一般≤20);
做表决:k 个样本中出现次数最多的类别,即为新数据的预测类别。
三、距离度量:KNN 的 "尺子" 怎么选?
计算样本相似度的 "尺子" 是 KNN 的关键,PPT 重点介绍了两种常用距离:
1. 欧式距离(最常用):
衡量多维空间中两点的直线距离,适用于连续特征。
二维空间:![]()
n 维空间:![]()
2. 曼哈顿距离(城市街区距离):
衡量两点在坐标轴上的绝对距离总和,适用于高维离散特征。
二维空间:![]()
四、实战案例 1:用 KNN 实现鸢尾花分类(sklearn 代码)
鸢尾花数据集是机器学习入门经典数据,包含 3 种鸢尾花的 4 个特征(花萼长度、宽度,花瓣长度、宽度)。用 KNN 实现分类的步骤如下:
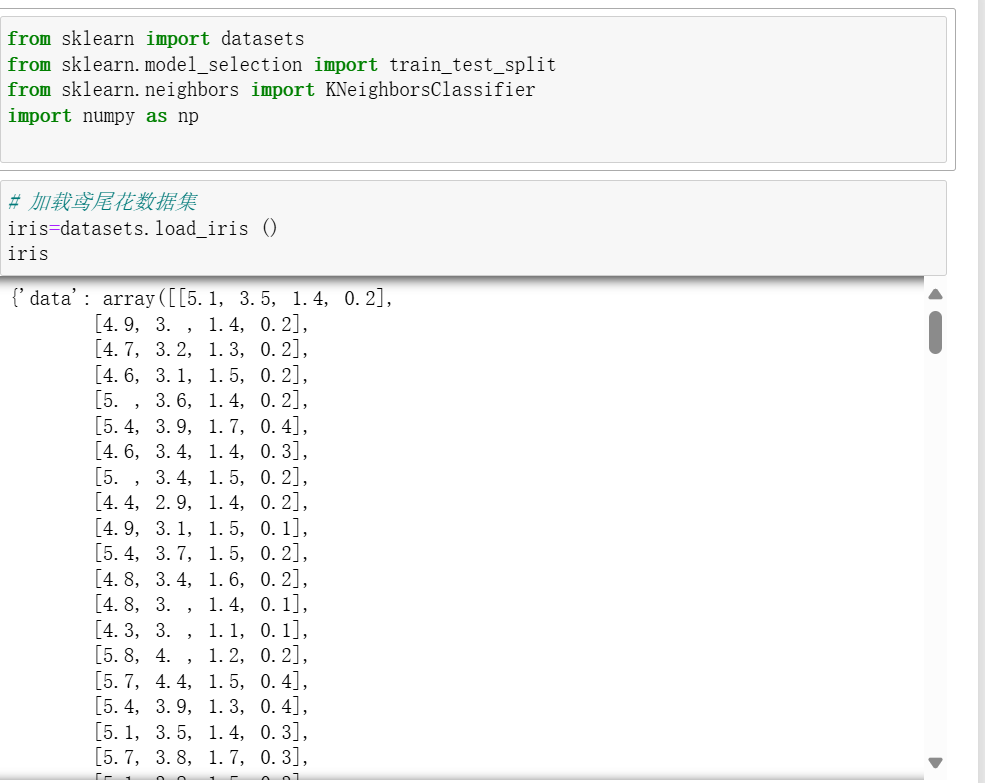
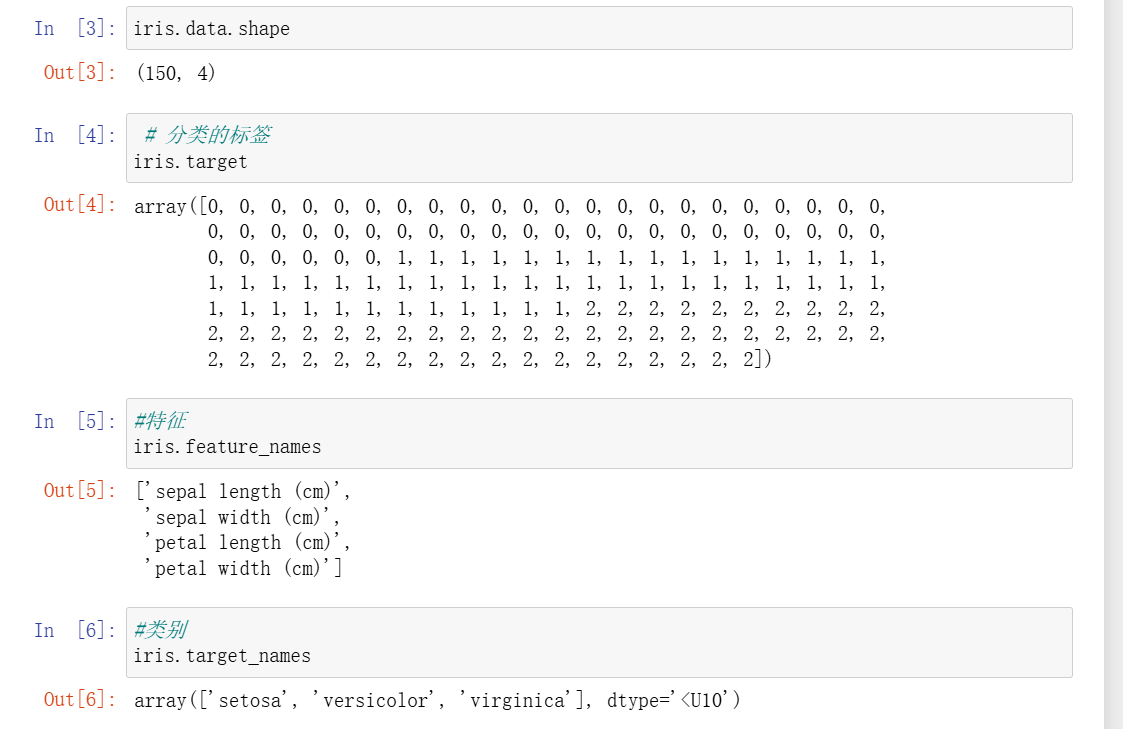
1. 加载数据集并查看信息:
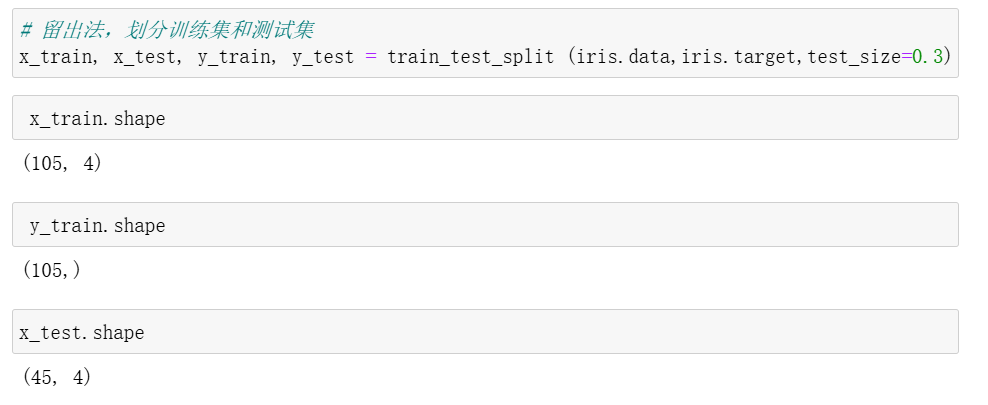
2. 划分训练集与测试集
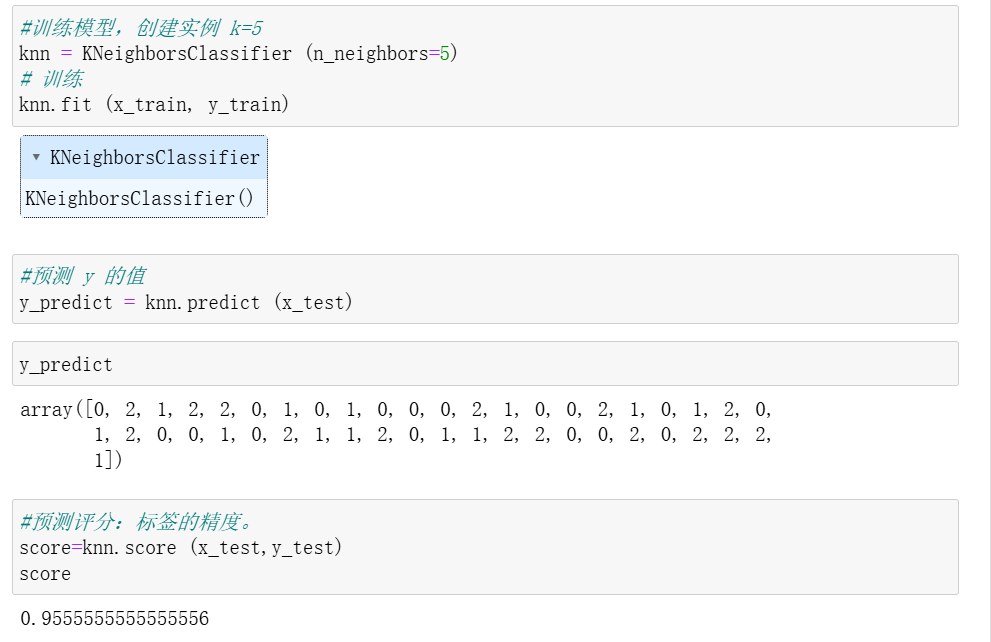
3. 构建 KNN 模型并训练
4. 选择k值
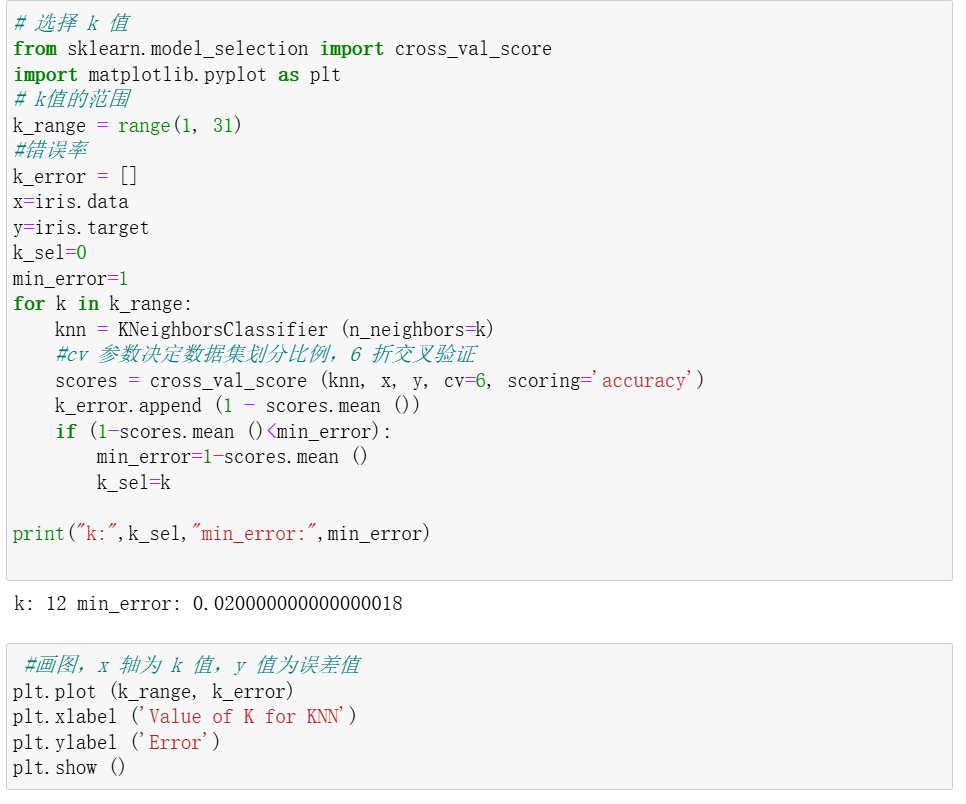
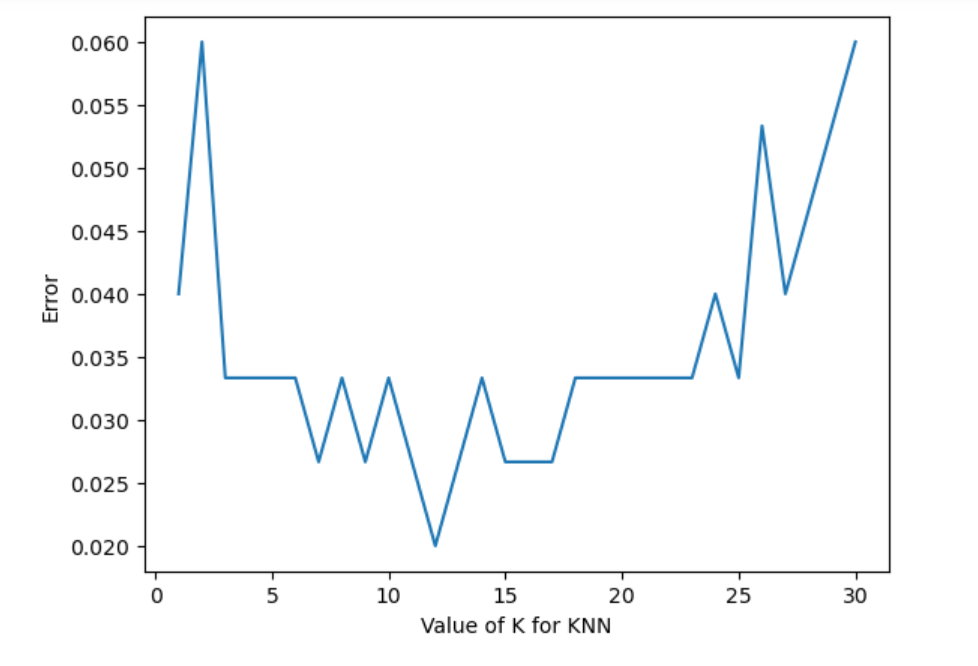
五、KNN 的优缺点与适用场景
优点:
简单直观,无需训练模型("懒学习"),易于理解和实现
对异常值不敏感,适合多分类问题
缺点:
计算成本高(预测时需与所有样本算距离),数据量大时效率低
对 k 值敏感(k 太小易过拟合,k 太大易欠拟合)
对不平衡数据不友好(多数类易主导预测)
适用场景:
小数据集分类任务(如鸢尾花识别、简单文本分类)
实时性要求不高的场景(因计算量大)
特征维度较低的情况(高维数据需先降维)
六、总结:KNN 是入门,更是理解 "相似性" 的钥匙
KNN 算法虽简单,却揭示了机器学习中 "相似性度量" 的核心思想。从电影分类到鸢尾花识别,其 "近邻表决" 的逻辑在生活中随处可见。掌握 KNN 不仅能解决简单分类问题,更能帮你理解复杂算法的底层逻辑 —— 毕竟,所有模型的本质都是寻找数据中的 "相似性" 与 "规律"。
