力扣（接雨水）——基于最高柱分割的双指针

深度解析 LeetCode 42. 接雨水：基于最高柱分割的双指针解法

一、题目剖析

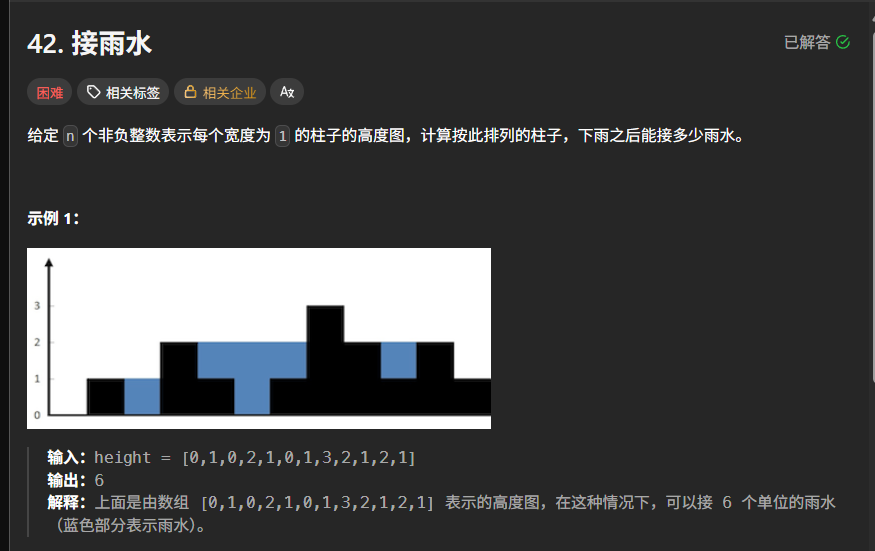
给定表示柱子高度的数组 height，需计算下雨后能承接的雨水总量。雨水留存的关键在于凹槽结构—— 左右两侧存在更高的柱子，中间柱子较低，形成储水空间。核心挑战是高效定位所有凹槽，计算其储水量。

二、算法思路：最高柱分割 + 双指针遍历

（一）核心思想

1. 最高柱定位：先找到数组中最高柱子的下标（rightMax 初始职责 ），以此为界，将数组分为左侧区域（最高柱左侧 ）和右侧区域（最高柱右侧 ）。
2. 分区域处理：
   • 左侧区域：从左向右遍历，维护 leftMax（遍历过的最高柱下标 ）。若当前柱子低于 leftMax，则可储水（储水量为 leftMax 与当前柱的高度差 ）；若当前柱子更高，则更新 leftMax。
   • 右侧区域：从右向左遍历，维护 rightMax（遍历过的最高柱下标 ）。若当前柱子低于 rightMax，则可储水（储水量为 rightMax 与当前柱的高度差 ）；若当前柱子更高，则更新 rightMax。
3. 双指针的隐含作用：通过分割后的单向遍历，每个区域的指针（如左侧的 curr ）承担“动态扫描 + 储水判断”的双职责，本质是简化的双指针逻辑。

（二）逻辑推导

最高柱是天然的“边界屏障”—— 左侧区域的储水仅受左侧更高柱限制（右侧有最高柱兜底 ），右侧区域同理。利用这一特性，可将复杂的双向边界判断，简化为两个单向遍历，降低逻辑复杂度。

三、代码实现与逐行解析

//双指针:得到当前元素的左侧的最大值当前元素的右侧最大值,Math.min(leftMax,rightMax)再减去当前元素的柱子高度,得到可以存的积水
//忽略头和尾因为一个左侧没有柱子一个右侧没有柱子,没有办法存水
class Solution {public int trap(int[] height) {if (height == null || height.length < 3) {return 0;}int leftMax = 0;int rightMax = 0;int sumRain = 0;//得到当前最高的柱子作为rightMax;for (int len = 0; len < height.length; len++) {if (height[len] > height[rightMax]) {rightMax = len;}}//遍历最高柱子的左侧柱子if (rightMax > 0) {for (int curr = 1; curr < rightMax; curr++) {//判断leftMax是否比当前柱子大,如果小就存不了水,替换leftMaxcontinueif (height[curr] >= height[leftMax]) {leftMax = curr;}//小于则可以存水,存水的大小是leftMax-currelse {sumRain += height[leftMax] - height[curr];}}}//遍历最高柱子的右侧柱子//由于是后序遍历此时左侧柱子的最大值为原先的rightMaxleftMax = rightMax;if (leftMax < height.length - 1) {rightMax = height.length - 1;for (int curr = height.length - 2; curr > leftMax; curr--) {if (height[rightMax] <= height[curr]) {rightMax = curr;} else {sumRain += height[rightMax] - height[curr];}}}return sumRain;}
}

（一）代码流程拆解

1. 边界处理：若数组为空或长度小于 3，直接返回 0（无法形成凹槽储水 ）。
2. 寻找全局最高柱：遍历数组，找到最高柱子的下标 rightMax，作为左右区域的分割点。
3. 处理左侧区域：
   • 若最高柱不在数组开头（rightMax > 0 ），从第二个柱子（下标 1 ）遍历到最高柱下标前一位（curr < rightMax ）。
   • 维护 leftMax（左侧遍历过的最高柱下标 ），当前柱低于 leftMax 时，计算储水量并累加；否则更新 leftMax。
4. 处理右侧区域：
   • 重置 leftMax 为全局最高柱下标，若最高柱不在数组结尾（leftMax < height.length - 1 ），从倒数第二个柱子（下标 length-2 ）遍历到最高柱下标后一位（curr > leftMax ）。
   • 维护 rightMax（右侧遍历过的最高柱下标 ），当前柱低于 rightMax 时，计算储水量并累加；否则更新 rightMax。
5. 返回结果：累加的储水量 sumRain 即为答案。

（二）关键逻辑解析

• 最高柱的分割作用：将数组分为左右两个独立区域，每个区域的储水仅受单侧最高柱限制（左侧区域右侧有全局最高柱兜底，右侧区域左侧有全局最高柱兜底 ），简化了边界判断。
• 单向遍历的高效性：左侧从左到右、右侧从右到左的遍历，避免了传统双指针的复杂条件判断，每个柱子仅遍历一次，时间复杂度为 O(n)。
• 储水量计算：利用“当前柱高度与遍历过的最高柱高度差”计算储水量，直接且高效，无需额外存储左右边界高度数组。

四、复杂度分析

（一）时间复杂度

• 寻找全局最高柱：O(n)（遍历数组一次 ）。
• 处理左侧区域：O(n)（最多遍历最高柱左侧所有柱子 ）。
• 处理右侧区域：O(n)（最多遍历最高柱右侧所有柱子 ）。
  总时间复杂度：O(n)（n 为数组长度 ），线性时间复杂度保证了高效性。

（二）空间复杂度

仅使用常数级额外变量（leftMax、rightMax、sumRain、curr ），空间复杂度：O(1)。