当前位置：首页 > news >正文

2025.8.24复习总结

news 2025/8/15 14:57:11

P2693 [USACO1.3] 号码锁 Combination Lock

题目背景

感谢 @Fond_Dream 提供五道 USACO 题目的标准题面。

题目描述

农夫约翰的奶牛不停地从他的农场中逃出来，导致了很多损害。为了防止它们再逃出来，他买了一只很大的号码锁以防止奶牛们打开牧场的门。

农夫约翰知道他的奶牛很聪明，所以他希望确保它们不会在简单地试了很多不同的号码组合之后就能轻易开锁。锁上有三个转盘，每个上面有数字 1 ~ n，因为转盘是圆的，所以 1 和 n 是相邻的。有两种能开锁的号码组合，一种是农夫约翰设定的，还有一种“预设”号码组合是锁匠设定的。但是，锁有一定的容错性，所以，在每个转盘上的数字都与一个合法的号码组合中相应的数字相距两个位置以内时，锁也会打开。

比如说，如果农夫约翰的号码组合是 ( 1 , 2 , 3 )，预设号码组合是 ( 4 , 5 , 6 )，在转盘被设定为 ( 1 , 4 , 5)（因为这和农夫约翰的号码组合足够接近）或 ( 2 , 4 , 8 )（因为这和预设号码组合足够接近）时可以打开锁。注意，( 1 , 5 , 6 )并不会打开锁，因为它与任一号码组合都不够接近。

给出农夫约翰的号码组合和预设号码组合，请计算能够开锁的不同的号码组合的数目。号码是有序的，所以 ( 1 , 2 , 3 ) 与 ( 3 , 2 , 1 ) 不同。

输入格式

输入的第一行是一个整数 n，代表锁上的数字个数。

输入的第二行有三个整数 x,y,z，代表农夫约翰的号码组合。

输入的第三行有三个整数 a,b,c，代表预设的号码组合。

输出格式

输出一行一个整数代表能够开锁的组合数目。

输入输出样例

输入 #1复制

50
1 2 3
5 6 7

输出 #1复制

说明/提示

输入输出样例 1 解释

每个转盘的标号是 1 ~ 50。农夫约翰的号码组合是 ( 1 , 2 , 3 )，预设号码组合是 ( 5 , 6 , 7 )。

数据规模与约定

对于 100% 的数据，保证 1≤n≤100，1≤x,y,z,a,b,c≤n。

#include<bits/stdc++.h>
using namespace std;
int n,a[4],b[4];
int g[110][110][110];
int main()
{cin>>n>>a[1]>>a[2]>>a[3]>>b[1]>>b[2]>>b[3];int m=250;int cnt=0;for(int i=a[1]-2;i<=a[1]+2;i++){for(int j=a[2]-2;j<=a[2]+2;j++){for(int k=a[3]-2;k<=a[3]+2;k++){if(!g[(i+n)%n][(j+n)%n][(k+n)%n])cnt++;g[(i+n)%n][(j+n)%n][(k+n)%n]=1;}}}for(int i=b[1]-2;i<=b[1]+2;i++){for(int j=b[2]-2;j<=b[2]+2;j++){for(int k=b[3]-2;k<=b[3]+2;k++){if(!g[(i+n)%n][(j+n)%n][(k+n)%n])cnt++;g[(i+n)%n][(j+n)%n][(k+n)%n]=1;}}}cout<<cnt;return 0;
}

解法：就是三重循环枚举，但是因为有建发所以会访问到负数，所以在作为下标时要加n再mod n，每次cnt++，输出cnt。

P2777 [AHOI2016初中组] 自行车比赛

题目描述

小雪非常关注自行车比赛，尤其是环滨湖自行车赛。一年一度的环滨湖自行车赛，需要选手们连续比赛数日，最终按照累计得分决出冠军。今年一共有 N 位参赛选手。每一天的比赛总会决出当日的排名，第一名的选手会获得 N 点得分，第二名会获得 N−1 点得分，第三名会获得 N−2 点得分，依次类推，最后一名会获得 1 点得分。保证没有选手会排名相同。

在之前的数日较量中，N 位选手已经分别累计了一些分数。现在即将开始的是最后一天的比赛。小雪希望知道有多少位选手还有可能获得最终的冠军，也就是说还有多少选手有可能通过最后一天的比赛获得累计总分第一名。

输入格式

第一行输入一个整数 N，表示参赛选手总数，保证 3≤N≤3×105。

之后 N 行，其中第 i 行输入一个整数 Bi 表示第 i 位选手已经获得的累计分数，满足 0≤Bi≤2×106。

输出格式

输出只有一行，只输出一个整数，表示有多少位选手有可能获得最终的冠军。

输入输出样例

输入 #1复制

输出 #1复制

输入 #2复制

输出 #2复制

说明/提示

数据范围及约定

对于 20% 的数据，3≤N≤600。
对于 50% 的数据，3≤N≤1×104。
对于 100% 的数据，3≤N≤3×105 且 0≤Bi≤2×106。

#include<bits/stdc++.h>
using namespace std;
int n,a[300010],b[300030];
int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}sort(a+1,a+n+1);int mx=0;for(int i=1;i<=n;i++){b[i]=a[i]+n-i+1;mx=max(b[i],mx);}int cnt=0;for(int i=1;i<=n;i++){if(a[i]+n>=mx){cnt++;}}cout<<cnt;return 0;
}

解法：先用一个数组b表示最后一轮比完之后的成绩，取最大值，如果有人大于等于最大值cnt++，输出cnt。

P1105 平台

题目描述

空间中有一些平台。给出每个平台的位置，请你计算从每一个平台的边缘落下之后会落到哪一个平台上。

注意，如果某两个平台的某个两边缘横坐标相同，物体从上面那个平台落下之后将不会落在下面那个平台上（即平台的范围是一个开区间，不包含端点）。平台可能会重叠。

从平台下落时视作从平台下方开始下落，也就是说不会落到高度相同的平台上。如果有两个平台的高度相同且都可以被落到的话，那么会落到编号靠前的那个平台。

输入格式

第一行有一个数 N 表示平台的个数;

接下来 N 行每行三个整数分别是平台的高度 Hi，左端点的 X 坐标 Li，右端点的 X 坐标 Ri。

其中，1≤N≤103，0≤H,L,R≤2×104。

输出格式

输出共 N 行，每行两个数，分别表示：

从第 i 个平台的左边缘落下后到达的平台序号和右边缘落下以后到达的平台序号。

输入数据中第一个平台的序号是 1。如果某个平台的某个边缘下面没有平台了，输出 0。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

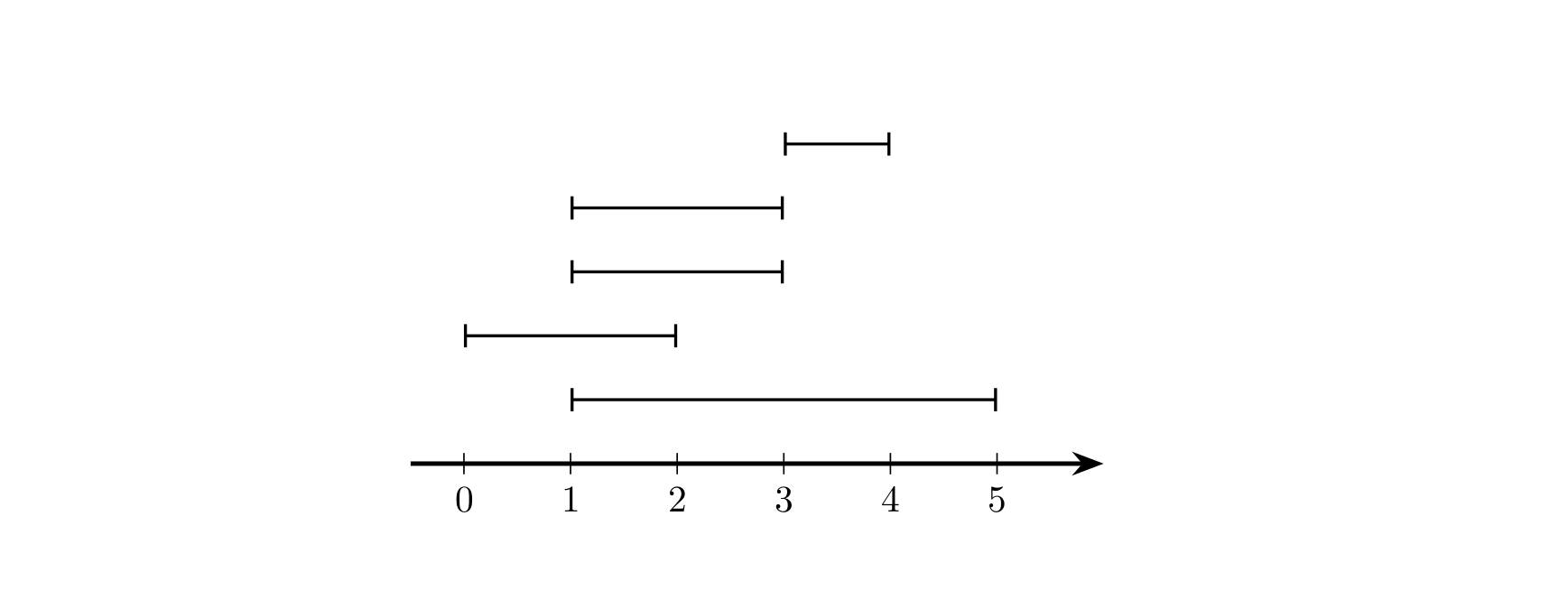
#include<bits/stdc++.h>
using namespace std;
int n,h[1010],a[1010],b[1010];
int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>h[i]>>a[i]>>b[i];}for(int i=1;i<=n;i++){int idx=0;for(int j=1;j<=n;j++){if(a[i]>a[j]&&a[i]<b[j]&&h[i]>h[j]){if(h[j]>h[idx]){idx=j;}}}cout<<idx;idx=0;for(int j=1;j<=n;j++){if(b[i]>a[j]&&b[i]<b[j]&&h[i]>h[j]){if(h[j]>h[idx]){idx=j;}}}cout<<" "<<idx<<"\n";}return 0;
}

解法：这道题就是判断一个平台的左端点和右端点分别在哪个平台内，所以就只需要一个循环嵌套来判断就行了，然后把序号保存下来输出。

查看全文

http://www.lryc.cn/news/621326.html