入门基础人工智能理论
目前人工智能绝对是一个如日中天的技术,现在AI时代不理解AI的原理,就如同互联网时代不上网一样。为此,我们也应该紧跟时代的潮流,持续学习 AI 相关的内容。
为此,我也准备全部投向AI,从今天开始,我将持续更新AI相关的学习博客,若你也有学习这方面的想法,不妨关注我一起成长。今天的内容,我们将从最基本的神经网络讲起,带你快速了解目前主要的AI技术。
本文是个人人工智能学习过程中学习和整理的文章,分享一下,共同进步。
神经网络:模拟大脑的计算模型
神经网络的设计灵感来源于人类大脑的工作原理。如果你曾经思考过大脑是如何处理信息的,你会发现一个有趣的现象:我们的大脑由数千亿个神经元组成,每个神经元都在接收信号、处理信息,然后将结果传递给其他神经元。这种看似简单的机制,却能产生我们所说的"智能"。
科学家们在研究大脑结构时发现,智能的本质就是通过收集信息,对不同的情景作出针对性的反应。既然大自然已经给出了实现智能的标准答案,那我们是否可以通过仿生的方式,模拟单个神经元的功能以及神经元之间的连接,从而在计算机中实现类似的智能呢?
从生物神经元到人工神经元
生物神经元包含几个核心组件:树突负责接收来自其他神经元的信号,细胞体整合所有输入信号,轴突传递处理后的信号,而突触则控制信号传递的强度。人工神经网络正是基于这种结构设计的。
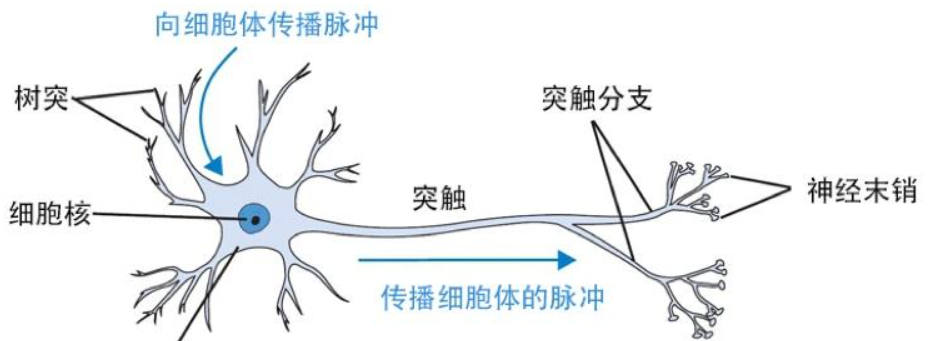
在人工神经元中,我们用数学方式模拟了这一过程。输入数据相当于树突接收的信号,每个输入都有一个对应的权重,这些权重就像突触强度一样,决定了不同输入的重要程度。神经元将所有加权输入求和,加上一个偏置项,然后通过激活函数产生输出。
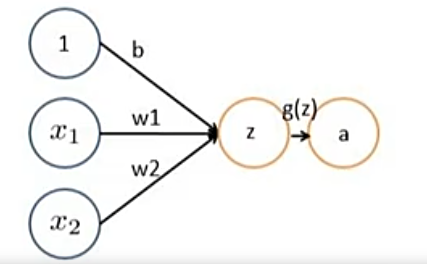
这个过程可以用一个简单的数学表达式描述:z = w₁x₁ + w₂x₂ + … + b,然后 A = g(z)。其中x是输入,w是权重,b是偏置,g是激活函数。
让我们以一个软件工程师选择技术栈的决策为例。假设你需要决定是否采用某个新技术,主要考虑两个因素:技术成熟度和团队熟悉程度。技术成熟度权重为6,团队熟悉程度权重为4。如果某技术成熟度为0.8,团队熟悉程度为0.6,那么决策函数就是:A = g(6×0.8 + 4×0.6 + b) = g(7.2 + b)。当这个值超过某个阈值时,你就会选择采用这个技术。
单层神经网络的局限性
虽然单个神经元能够处理一些基本的分类问题,但很快研究者们就发现了它的局限性。1969年,马文·明斯基和西摩·帕普特在他们的著作中指出,单层神经网络无法解决线性不可分的问题,最典型的例子就是XOR(异或)问题
XOR问题看起来很简单:当两个输入相同时输出0,不同时输出1。但是单层神经网络无论如何调整权重,都无法正确分类所有情况。这是因为XOR问题本质上是非线性的,而单层网络只能实现线性分离。也就是说,不能通过一条直线(或平面)将输入空间中的不同类别完全分开。
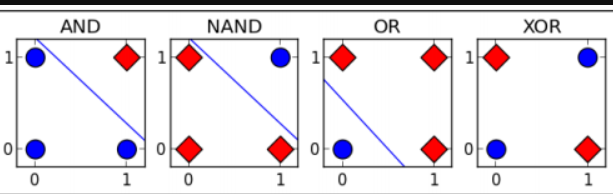
这个发现对整个神经网络领域造成了巨大冲击,直接导致了第一次"AI寒冬"。研究者们意识到,要解决复杂的现实问题,需要更强大的网络结构。
多层感知机:突破线性约束
神经网络具有自己的局限性,就像我们的大脑一样,是由上千亿个神经元连接而成。如果想要让神经网络产生更大的智能效果,我们就需要把多个神经元层层连接起来,这就是多层感知机(MLP)的核心思想。
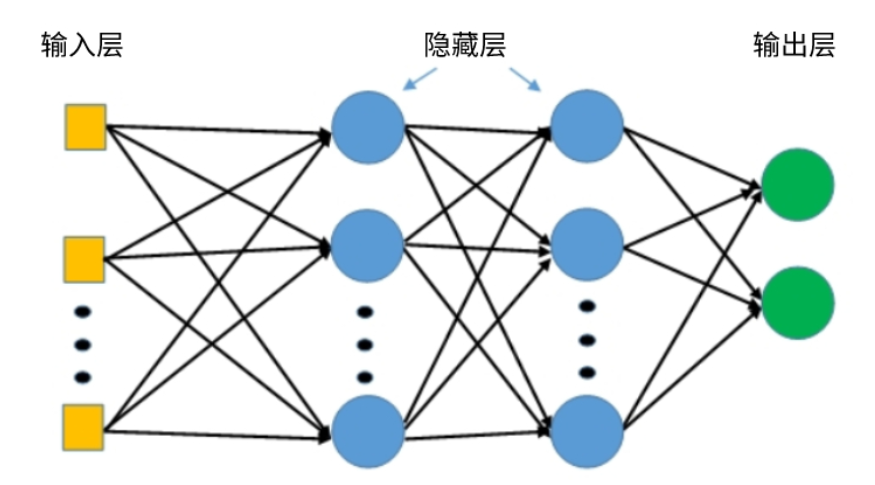
MLP的架构设计
多层感知机在单层感知机的基础上添
加了一个或多个隐藏层。典型的MLP包含三个部分:输入层接收原始数据,隐藏层进行特征变换和非线性映射,输出层产生最终预测结果。
隐藏层的引入彻底改变了网络的能力。通过多层非线性变换,MLP能够学习复杂的输入输出映射关系。理论上,具有足够隐藏神经元的单隐藏层MLP可以逼近任何连续函数,这被称为通用逼近定理。
这种能力的关键在于激活函数的非线性特性。每个隐藏神经元通过加权输入和激活函数,生成一个基础的非线性变换。当神经元数量足够多时,这些基础变换可以组合出复杂的函数形状,从而解决线性不可分的问题。
数学家已经证明,神经网络理论上可以拟合任何函数。
想象一下你在用乐高积木搭建一个复杂的城堡。单个积木很简单,但只要积木够多、层次够丰富,你就能搭出任何想要的形状。神经网络就是这个道理。
每个神经元本质上就是一个"选择开关"。给它一个输入,它要么激活(输出1),要么不激活(输出0)。用数学语言说,一个神经元可以把整个输入空间分成两半 - 一半说"是",一半说"不"。每个神经元都把输入空间切一刀,当你有足够多的神经元时,就能把整个空间切成非常非常细的小块。每一小块,你都可以单独决定输出什么值。
而任何复杂的函数,都可以用一堆"阶梯状"的简单函数来逼近。
- 用1个矩形去逼近 → 很粗糙
- 用10个小矩形去逼近 → 好一些
- 用1000个细矩形去逼近 → 看起来就很像圆了
- 用无穷多个矩形 → 完全就是圆形
神经网络做的就是这件事!每增加一个神经元,就相当于增加了一个"可调节的矩形"。
训练的挑战:隐藏层问题
然而,MLP的训练比单层网络复杂得多。在单层网络中,我们知道每个训练样本的正确输出,可以直接比较网络输出与正确答案,然后调整权重。但在MLP中,隐藏层没有"正确答案"。
当网络输出错误时,我们不知道该如何调整隐藏层的权重。这就像一个软件项目出现bug,我们知道最终结果是错的,但不知道是哪个模块、哪行代码的问题。这个被称为"信用分配问题"的难题,在很长时间内阻碍了多层网络的发展。
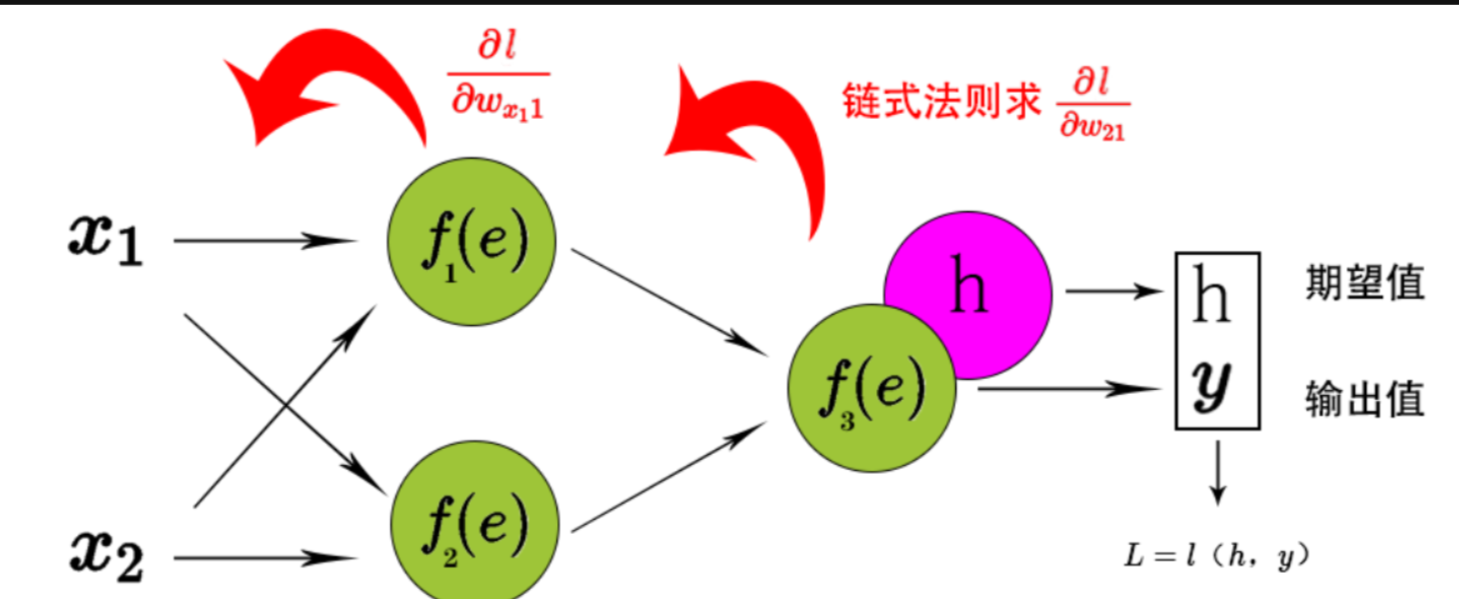
反向传播算法:解决信用分配问题
1980年代,反向传播算法的出现彻底解决了这个问题。这个算法基于微积分中的链式法则,能够计算网络中每个权重对最终误差的贡献。要理解反向传播的重要性,我们需要深入了解它的工作原理。
反向传播的数学基础:链式法则
反向传播的核心是链式法则。在多层网络中,最终的误差是多个函数复合的结果。假设我们有一个简单的三层网络:输入层 → 隐藏层 → 输出层。最终误差E是输出的函数,输出是隐藏层的函数,而隐藏层又是输入的函数。
如果我们想知道某个权重w对误差E的影响,需要计算∂E/∂w。但这个权重可能在网络的深层,它对误差的影响需要通过多个中间层传递。链式法则告诉我们:
∂E/∂w = (∂E/∂output) × (∂output/∂hidden) × (∂hidden/∂w)
这就像一个责任传递链:最终误差的责任,通过每一层的函数关系,最终分配到每个权重上。
反向传播的四个关键步骤
步骤1:前向传播
数据从输入层流向输出层,每一层计算加权和并通过激活函数:
- 隐藏层:h = f(W1 × x + b1)
- 输出层:y = g(W2 × h + b2)
步骤2:计算损失
比较预测输出y与真实标签t,计算损失函数:
- L = ½(y - t)²(以均方误差为例)
步骤3:反向传播计算梯度
从输出层开始,逐层计算梯度:
- 输出层梯度:∂L/∂W2 = (y - t) × h
- 隐藏层梯度:∂L/∂W1 = (y - t) × W2 × f’(z1) × x
这里的关键是误差信号如何从后向前传播。每一层都接收来自后一层的误差信号,计算自己的责任,然后将修正后的误差信号传递给前一层。
步骤4:参数更新
使用计算出的梯度更新权重(这里就需要梯度下降):
- W = W - α × ∂L/∂W
详细实例:手写数字识别网络
让我们用一个具体的例子来理解反向传播的完整过程。假设我们要训练一个识别手写数字的网络,结构如下:
- 输入层:784个神经元(28×28像素)
- 隐藏层:128个神经元
- 输出层:10个神经元(0-9数字)

场景设置:输入一张数字"3"的图片,但网络错误地预测为"8"。
前向传播过程
- 输入处理:784个像素值输入网络
- 隐藏层计算:h = sigmoid(W1 × x + b1),得到128个隐藏层激活值
- 输出层计算:y = softmax(W2 × h + b2),得到10个类别概率
- 错误结果:y[3] = 0.2(数字3的概率),y[8] = 0.7(数字8的概率)
反向传播过程
第一步:输出层误差计算
目标:y[3] = 1.0, y[8] = 0.0
当前:y[3] = 0.2, y[8] = 0.7
误差:δ_output[3] = 0.2 - 1.0 = -0.8,δ_output[8] = 0.7 - 0.0 = 0.7
第二步:输出层权重梯度
对于连接隐藏层第i个神经元到输出层第j个神经元的权重W2[i][j]:
∂L/∂W2[i][j] = δ_output[j] × h[i]
例如,如果隐藏层第50个神经元的激活值是0.6:
- ∂L/∂W2[50][3] = -0.8 × 0.6 = -0.48
- ∂L/∂W2[50][8] = 0.7 × 0.6 = 0.42
第三步:隐藏层误差计算
隐藏层的误差是所有输出层误差的加权和:
δ_hidden[i] = Σ(δ_output[j] × W2[i][j]) × sigmoid’(z1[i])
第四步:隐藏层权重梯度
∂L/∂W1[k][i] = δ_hidden[i] × x[k]
梯度下降:权重更新的引擎
反向传播计算出了每个权重的梯度,但这只是告诉我们"应该往哪个方向调整权重"。梯度下降决定了"调整多少"和"如何调整"。
梯度下降的几何直观
在参数空间中,损失函数形成一个多维曲面。我们的目标是找到这个曲面的最低点。梯度就像山坡的坡度向量,指向上坡最陡的方向。要下山(降低损失),我们应该朝梯度的反方向移动。
权重更新公式:W_new = W_old - α × ∇L
其中α是学习率,控制每次更新的步长。
学习率的关键作用
学习率过大的问题:
如果学习率设为1.0,在我们的例子中:
- W2[50][3] = W2[50][3] - 1.0 × (-0.48) = W2[50][3] + 0.48
- W2[50][8] = W2[50][8] - 1.0 × 0.42 = W2[50][8] - 0.42
这样的大幅调整可能导致权重震荡,永远无法收敛。
学习率适中的情况:
如果学习率设为0.01:
- W2[50][3] = W2[50][3] + 0.0048
- W2[50][8] = W2[50][8] - 0.0042
这样的小幅调整让网络逐步改善。
反向传播与梯度下降的完美配合
反向传播和梯度下降形成了一个完整的学习循环:
- 反向传播的责任:精确计算每个参数对误差的影响程度(梯度)
- 梯度下降的责任:根据梯度信息,决定如何调整参数
- 迭代优化:重复这个过程,网络性能逐步提升
在我们的数字识别例子中,经过多次迭代后:
- 连接到数字"3"输出的权重逐渐增大
- 连接到数字"8"输出的权重逐渐减小
- 隐藏层学会提取有利于区分"3"和"8"的特征
现代优化技术
传统的梯度下降存在一些问题,现代深度学习使用更高级的优化器:
Adam优化器结合了动量和自适应学习率:
- 维护每个参数的历史梯度信息
- 自动调整学习率
- 在平坦区域加速,在陡峭区域减速
批处理策略:
- 批量梯度下降:使用全部数据计算梯度,稳定但慢
- 随机梯度下降:使用单个样本,快速但有噪声
- 小批量梯度下降:使用小批量数据,平衡效率和稳定性
这就是为什么反向传播算法被誉为深度学习的基石。它不仅解决了多层网络的训练问题,更重要的是建立了一套系统的、可扩展的学习框架。结合梯度下降,这套机制让我们能够训练任意深度的网络,为现代深度学习的发展奠定了坚实基础。
MLP的应用与局限
MLP在图像识别、语音处理、医疗诊断、金融分析等领域都有广泛应用。它的出现标志着人工智能历史上的重要转折点,结束了第一次AI寒冬,重新激发了对神经网络的兴趣。
但MLP也有明显的局限性。首先是梯度消失问题,在很深的网络中,误差信号在反向传播过程中会逐渐衰减,导致前面几层几乎学不到东西。其次,MLP无法利用数据的空间或时序结构,这限制了它在图像和序列数据上的表现。
正是这些局限性,促使研究者们开发了专门的网络架构来处理特定类型的数据。
卷积神经网络:专为视觉设计的架构
MLP虽然能够处理图像数据,但效果并不理想。当我们将一张28×28的图像输入MLP时,需要将其展平成784个像素点,这个过程完全丢失了图像的空间结构信息。想象一下,这就像把一个精心设计的用户界面拆解成单独的按钮和文本框,然后期望程序能理解整体的布局逻辑。
CNN的设计原理
卷积神经网络(CNN)的设计灵感来自于1959年神经生物学家的一个重要发现。他们在研究猫的视觉皮层时发现,某些神经元只对特定方向的边缘敏感,而另一些神经元则对位置变化不敏感。这种层次化的特征检测机制启发了CNN的设计。
CNN的核心创新在于三个概念:局部连接、权重共享和池化操作。
局部连接意味着每个神经元只关注输入的一小块区域,而不是全部像素。这类似于程序中的模块化设计,每个模块只处理特定的功能,而不是一个庞大的单体程序。
权重共享是CNN的另一个关键特性。同一个卷积核在整个图像上滑动,使用相同的权重参数。这就像定义了一个可复用的函数,无论在代码的哪个位置调用,其行为都是一致的。比如边缘检测器,无论在图像的哪个位置,检测边缘的逻辑都是相同的。
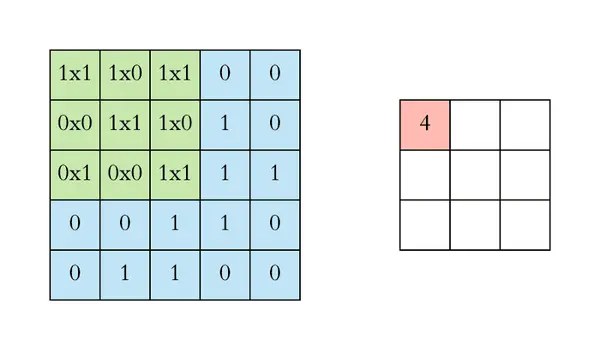
卷积操作的本质
卷积操作可以理解为一种模式匹配机制。一个3×3的卷积核实际上是一个小模板,它在图像上滑动,计算每个位置的匹配程度。
在实际应用中,不同类型的边缘检测器有不同的权重配置。水平边缘检测器通常设计为:
[ 1, 1, 1]
[ 0, 0, 0]
[-1, -1, -1]
而垂直边缘检测器则是:
[ 1, 0, -1]
[ 1, 0, -1]
[ 1, 0, -1]
这样的设计有其深层的原理。以水平边缘检测器为例,上方区域使用正权重,中间区域为零,下方区域使用负权重。当卷积核扫过一个水平边缘(比如上亮下暗的区域)时,上方的亮像素乘以正权重得到大正数,下方的暗像素乘以负权重也得到大正数,两者相加产生强烈的响应。但是当扫过平坦区域时,由于所有像素值相似,正负权重的效果会相互抵消,输出接近零。
这种权重设计遵循几个重要原则。首先是零和原则,即所有权重之和应该为0,这确保了在均匀区域不会产生响应。其次是对称性原则,好的边缘检测器应该对正负边缘有相同的敏感度。最后是对比增强原则,相邻区域使用相反符号的权重来增强边缘对比度。
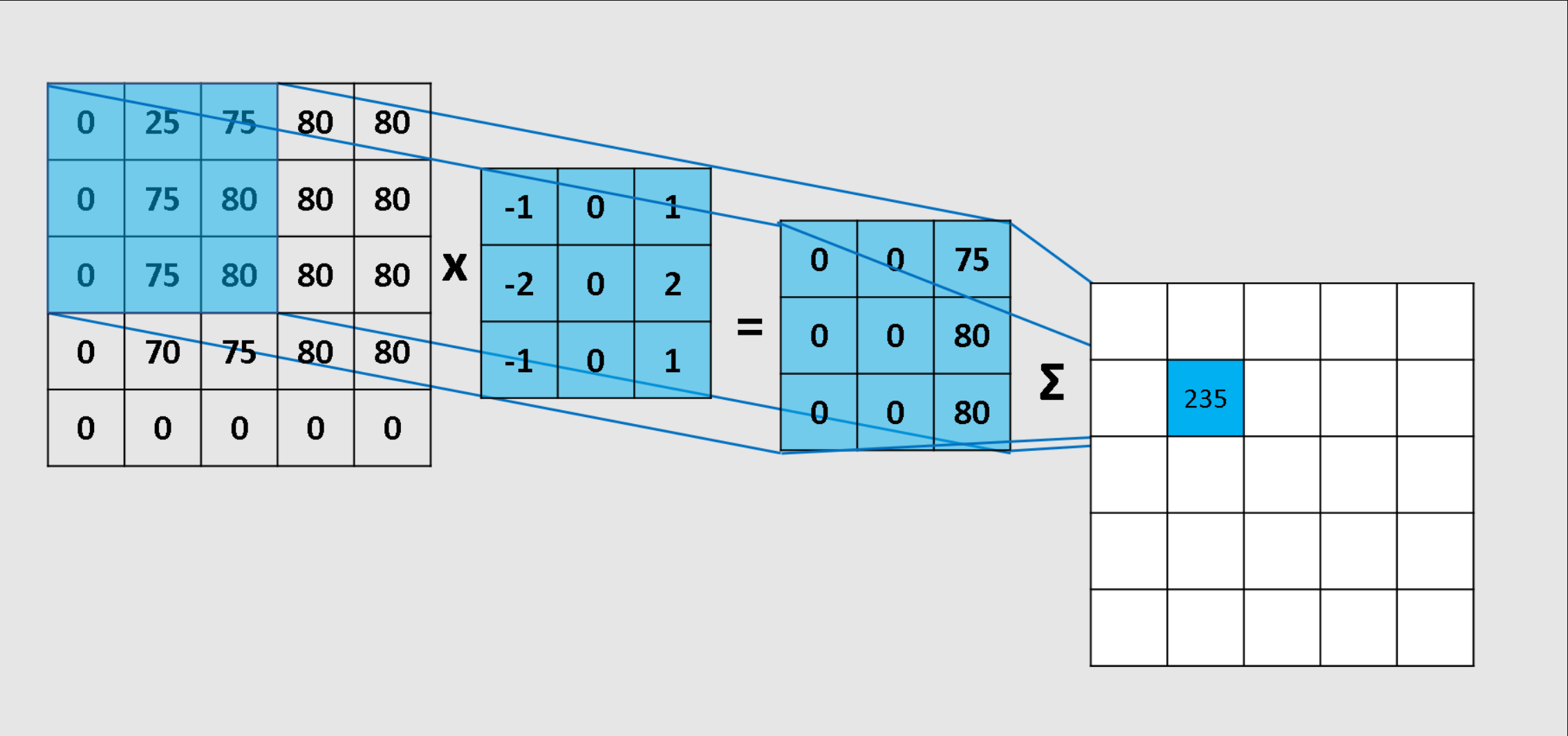
在计算机视觉中,Sobel算子是使用最广泛的边缘检测器之一。它在简单边缘检测的基础上加入了平滑效果,比如垂直Sobel算子:
[-1, 0, 1]
[-2, 0, 2]
[-1, 0, 1]
这里中间列的权重是±2而不是±1,原因是中间位置更接近真正的边缘位置,给予更大的权重相当于进行了加权平均,这样可以减少噪声影响,让检测结果更加稳定和准确。
让我们用一个具体的数值例子来验证这个原理。假设有一个图像区域,上半部分像素值为100,下半部分像素值为50。使用水平边缘检测器进行卷积:100×1 + 100×1 + 100×1 + 100×0 + 100×0 + 100×0 + 50×(-1) + 50×(-1) + 50×(-1) = 300 + 0 - 150 = 150。这个较大的正值表明检测到了边缘。而在完全平坦的区域,所有像素值都是100的情况下,计算结果是:300 + 0 - 300 = 0,没有响应。
实际上,在现代的CNN中,这些卷积核的权重并不是人工预设的,而是通过训练过程自动学习得到的。网络会根据具体的任务需求,自动学习出最适合的特征检测器。但有一个有趣的现象是,训练好的CNN的第一层卷积核往往会自发地学习出类似Sobel、Gabor等经典边缘检测器的模式,这从侧面证实了这些传统算子设计的合理性和有效性。
这种设计让CNN能够自动学习各种特征检测器:低层学习边缘和纹理,中层学习形状和模式,高层学习复杂的对象部件。这种层次化特征学习是CNN强大表现力的关键。
池化与特征抽象
池化操作进一步增强了CNN的能力。最大池化从每个小区域中选择最大值,这实现了两个目的:降低特征图的空间尺寸,提高计算效率;增强对小幅平移的不变性,使网络对图像中对象的微小位移更加鲁棒。
池化操作类似于在软件设计中的抽象层概念。就像我们会将底层的系统调用抽象为高级API一样,池化将局部的细节特征抽象为更加概括的表示。
CNN的应用领域
CNN在计算机视觉领域取得了革命性的成功。在图像分类任务中,CNN能够准确识别照片中的对象;在目标检测中,它不仅能识别对象类型,还能定位对象在图像中的位置;在图像分割任务中,CNN能够对每个像素进行精确分类。
除了视觉任务,CNN还被成功应用于自然语言处理、推荐系统等领域,展现了其强大的适应性。
CNN的技术局限
尽管CNN在视觉任务上表现出色,但它也有明显的局限性。首先是计算复杂度高,大量的卷积运算需要强大的GPU支持。其次,CNN对于被遮挡的对象识别效果较差。最重要的是,CNN缺乏处理序列数据的能力,无法建模时间依赖关系。
当我们需要处理文本、语音或时间序列数据时,CNN的这些局限就变得明显了。这促使研究者们开发了专门处理序列数据的网络架构。
循环神经网络:为序列数据而生
传统的神经网络,包括MLP和CNN,在处理每个输入时都是独立的,就像无状态的函数一样。但现实中的许多任务需要理解上下文和时序关系。比如在理解一句话时,我们需要记住前面的词汇才能理解后面的内容;在语音识别中,当前的音素需要结合前面的语音信息才能准确识别。
RNN的记忆机制
循环神经网络(RNN)引入了记忆机制来解决这个问题。RNN的核心思想可以用一个简单的递推关系表达:当前时刻的隐藏状态是前一时刻隐藏状态和当前输入的函数。
在数学上,这表示为:h_t = f(W_hh × h_{t-1} + W_xh × x_t + b),其中h_t是当前隐藏状态,x_t是当前输入,W是权重矩阵,f是激活函数。
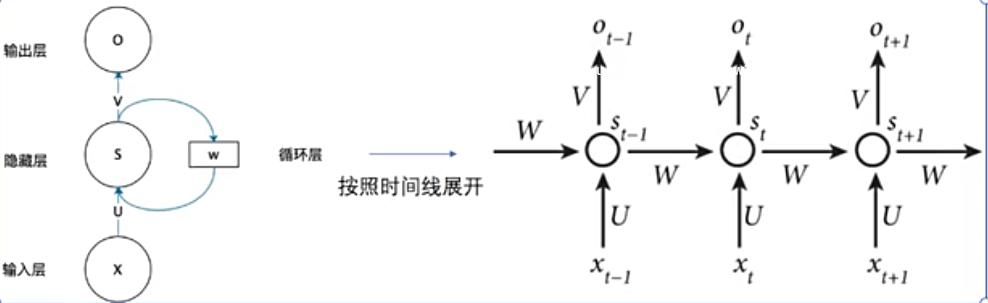
这种设计让RNN具备了"记忆"能力。隐藏状态就像程序中的实例变量,它在处理序列的过程中不断更新,积累历史信息。与传统的无状态函数不同,RNN的输出不仅依赖于当前输入,还依赖于所有历史输入的累积效果。
权重共享的优势
RNN的另一个重要特性是在时间维度上的权重共享。无论处理序列的哪个位置,RNN都使用相同的权重参数。这类似于在程序中定义一个递归函数,无论递归到第几层,函数的逻辑都保持一致。
这种设计带来了两个显著优势:参数效率和泛化能力。参数效率体现在无论序列长度如何变化,RNN的参数数量都保持固定。泛化能力体现在网络学会的模式可以应用于序列的任意位置。
实例:情感分析的完整过程
让我们通过一个具体的情感分析例子来深入理解RNN的工作机制。假设我们要训练一个RNN来判断电影评论的情感,网络结构如下:
- 词汇表大小:10000个词汇
- 词向量维度:128维
- 隐藏层维度:64维
- 输出:正面/负面(2分类)
现在输入一句评论:“这部电影真的很精彩”,看看RNN如何逐步处理这个序列。
首先进行词汇编码和嵌入。"这部"编码为ID 1024,通过词嵌入矩阵转换为128维向量;"电影"编码为ID 567,"真的"编码为ID 2341,"很"编码为ID 89,"精彩"编码为ID 4567。每个词都被转换为对应的128维密集向量表示。
接下来是RNN的逐步处理过程。初始时,隐藏状态h0是一个64维的零向量。
第一步处理"这部":输入x1是"这部"的128维词向量,计算h1 = tanh(W_hh × h0 + W_xh × x1 + b)。由于h0是零向量,实际上h1主要由词"这部"的信息决定。假设计算结果h1 = [0.1, -0.3, 0.7, …],这个向量开始编码序列的初始信息。
第二步处理"电影":输入x2是"电影"的词向量,计算h2 = tanh(W_hh × h1 + W_xh × x2 + b)。这时h2不仅包含"电影"的信息,还通过h1携带了"这部"的信息。网络开始理解这是关于电影的讨论。假设h2 = [0.3, 0.1, 0.5, …]。
第三步处理"真的":h3 = tanh(W_hh × h2 + W_xh × x3 + b)。"真的"是一个程度副词,表示强调。网络通过h3积累了"这部电影真的"的语义信息,可能h3 = [0.5, 0.4, 0.8, …],情感倾向开始显现。
第四步处理"很":继续处理程度副词"很",h4进一步强化了情感的强度信息。
第五步处理"精彩":这是关键的情感词汇。"精彩"是明显的正面评价词,h5 = tanh(W_hh × h4 + W_xh × x5 + b)会显著向正面情感倾斜,可能得到h5 = [0.8, 0.7, 0.9, …]。
最后进行情感分类。将最终的隐藏状态h5输入到输出层:y = softmax(W_out × h5 + b_out)。输出是一个2维向量,表示负面和正面的概率。在这个例子中,可能得到y = [0.15, 0.85],表示85%的概率是正面情感。
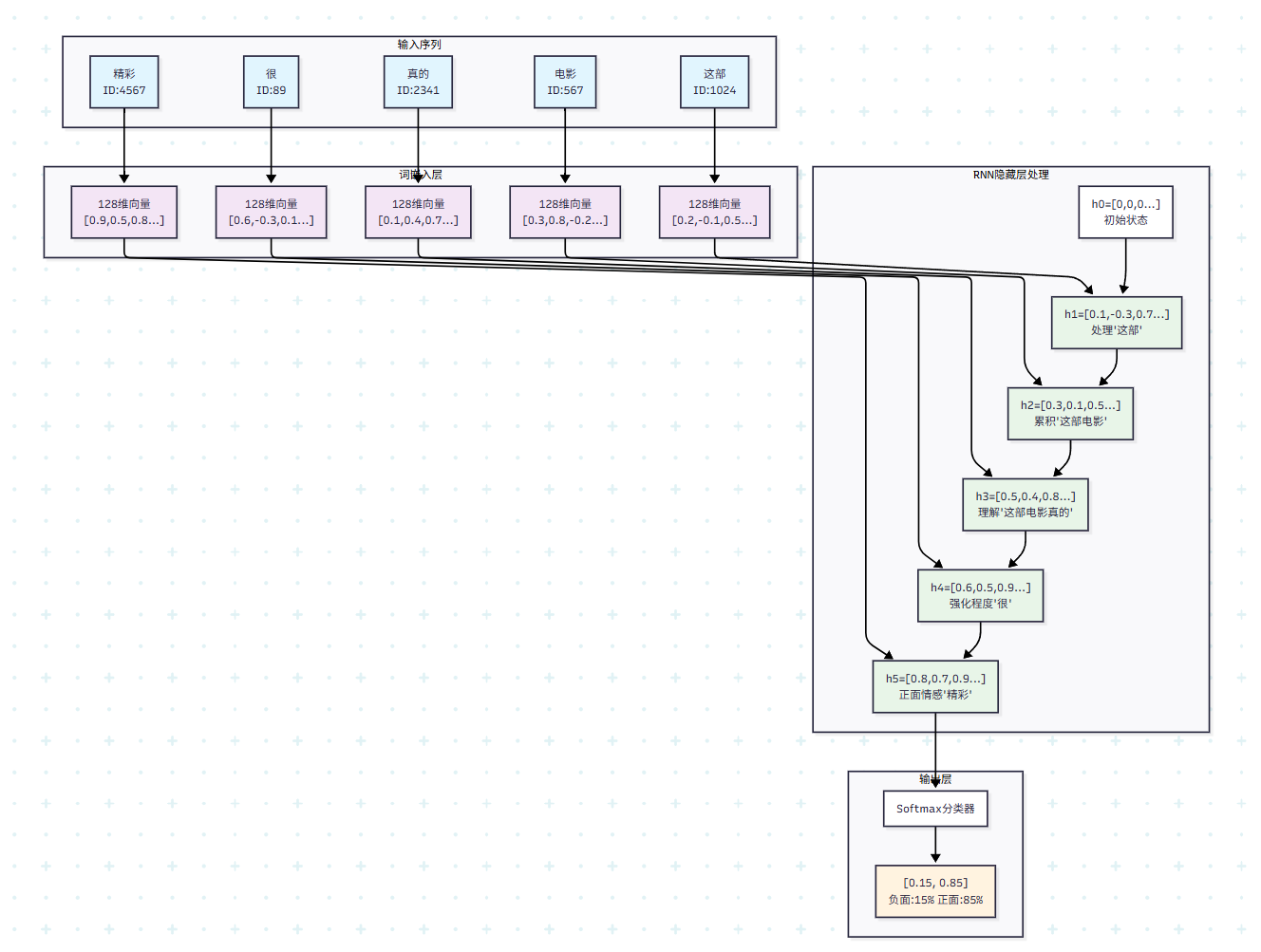
在训练过程中,如果真实标签是正面([0, 1]),那么损失为交叉熵损失。然后通过时间反向传播算法,误差会从输出层反向传播到每个时间步,更新所有的权重参数。
这个例子展现了RNN的几个关键特性。首先是序列建模能力,每个词的处理都考虑了前面所有词的信息。其次是上下文理解,"精彩"这个词在不同上下文中可能有不同含义,但在"电影"的上下文中明确表示正面评价。最后是情感累积效应,"真的"和"很"这些程度词会逐步增强最终情感的强度。
当然,这个简化的例子也暴露了RNN的局限性。如果句子很长,比如"这部电影真的很精彩,但是剧情有些拖沓,总体来说还是值得推荐的",那么早期的正面情感信息可能在处理到后面的转折时被淡化,这就是著名的梯度消失问题的实际体现。
RNN的应用场景
RNN在自然语言处理领域发挥了重要作用。在语言建模中,RNN通过学习大量文本数据,能够预测下一个最可能出现的词汇,这是智能输入法和文本生成的基础。在机器翻译中,RNN能够理解源语言句子的语法结构,然后生成目标语言的对应表达。
在语音处理方面,RNN能够处理语音信号的时序特性,实现语音识别和语音合成。在时间序列预测中,RNN可以基于历史数据预测未来趋势,应用于股价预测、天气预报等场景。
RNN的关键缺陷
然而,RNN也存在一些严重的技术问题。最主要的是梯度消失问题:当序列很长时,早期的信息在反向传播过程中会逐渐衰减,导致网络无法学习长期依赖关系。
在数学上,这是因为梯度需要通过多个时间步进行链式传播,而每一步的梯度通常小于1,连续相乘会导致指数级衰减。这就像信号在长距离传输中会逐渐衰减一样。
另一个问题是训练效率低下。由于RNN的顺序依赖性,无法像CNN那样并行处理,这限制了在现代GPU架构上的训练速度。
技术演进的方向
为了解决这些问题,研究者们开发了更先进的架构。LSTM(长短期记忆网络)通过引入门控机制,有效缓解了梯度消失问题。GRU(门控循环单元)在保持LSTM优势的同时简化了结构。
更重要的是,Attention机制的提出彻底改变了序列建模的范式。通过让模型直接关注序列中的相关部分,而不是依赖隐藏状态的顺序传递,Attention机制催生了Transformer架构,为现代大语言模型奠定了基础。
从神经网络到MLP,再到CNN和RNN,我们看到了人工智能技术的不断演进。每一种架构都是为了解决前一代技术的局限性而产生的,同时也为下一代技术的发展铺平了道路。理解这些基础架构的原理和演进逻辑,对于深入掌握现代AI技术具有重要意义。
现代的深度学习已经远远超越了这些基础架构,但它们的核心思想——层次化特征学习、参数共享、注意力机制等——仍然是当前最先进AI系统的重要组成部分。通过深入理解这些基础概念,我们能够更好地把握AI技术的发展脉络,为进一步学习更复杂的架构打下坚实基础。
