数据结构:中缀到后缀的转换(Infix to Postfix Conversion)
目录
一切的起点:我们习惯的数学写法(中缀表达式)
中缀表达式的问题:计算机的“困惑”
后缀表达式 (Postfix Notation)
前缀表达式 (Prefix Notation)
三种表达式的对比与用途
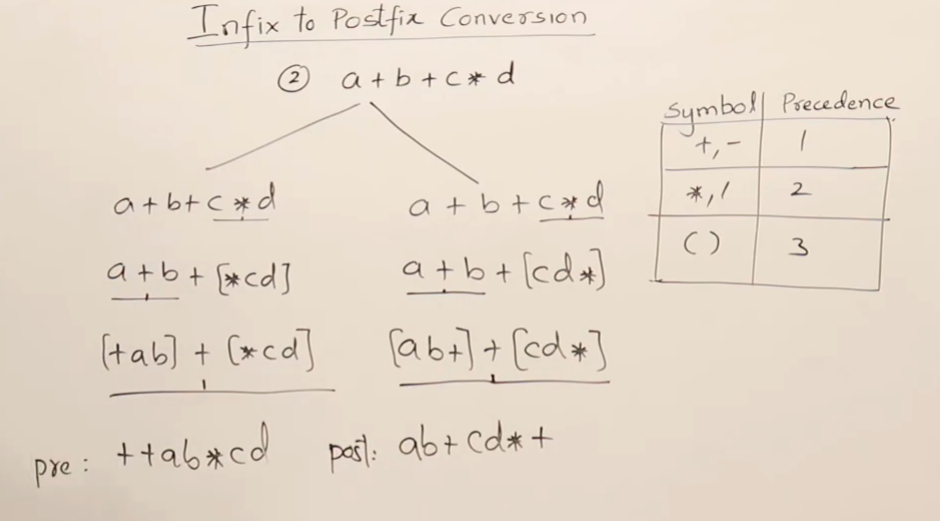
手动转换(Manual Conversion)
1. 遇到操作数(operand)(a, b, c, d, e)
2. 遇到操作符(operator)(+, *, -, /)
3. 遇到括号
4. 遇到字符串末尾
手动转换示例:a + b * c - (d + e)
一切的起点:我们习惯的数学写法(中缀表达式)
当我们要计算“3加4”,我们会怎么写?
我们自然而然地会写成 3 + 4。
在这个表达式里,操作符 + 被放在了两个操作数 3 和 4 的中间。这种将操作符放在中间的表示方法,就叫做中缀表达式 (Infix Notation)。
这是人类最习惯、最直观的读写方式。我们从小学的数学课本到大学的教科书,几乎所有的数学公式都是中缀表达式,例如: a + b - c , (a + b) * c。
中缀表达式的问题:计算机的“困惑”
我们来看一个稍微复杂一点的中缀表达式:3 + 4 * 5。
作为人类,我们受过训练,知道要“先算乘除,后算加减”。我们会先计算 4 * 5 = 20,然后再计算 3 + 20 = 23。
但如果一个计算机程序傻傻地从左到右读取这个表达式,它会怎么做?
-
读到
3 -
读到
+ -
读到
4,它可能会立刻计算3 + 4 = 7 -
读到
* -
读到
5,它接着计算7 * 5 = 35
结果是35,这显然是错误的。
中缀表达式对人类友好,但对计算机来说,存在两个巨大的问题:
-
运算顺序不确定:单纯从左到右的顺序,不一定是真正的运算顺序。
-
依赖额外规则:为了解决顺序问题,我们引入了两个额外的、对计算机来说很麻烦的规则:
-
优先级 (Precedence):规定了
*和/的优先级高于+和-。 -
括号 (Parentheses):我们可以用
( )强制改变运算顺序,例如(3 + 4) * 5。
-
这意味着,计算机在处理中缀表达式时,不能简单地进行线性读写,它需要反复扫描、需要内置一张优先级表、还需要处理复杂的括号嵌套逻辑。这套流程非常低效和复杂。
核心问题引出: 有没有一种表示方法,它本身就包含了运算顺序,完全不需要依赖优先级或括号,能让计算机从头到尾扫一遍就直接算出结果?
问题的解决方案:后缀和前缀表达式
为了解决计算机的“困惑”,数学家们(特别是波兰逻辑学家扬·武卡谢维奇)发明了两种新的表示法。
后缀表达式 (Postfix Notation)
核心思想: 将操作符放到两个操作数的后面。
-
3 + 4变成3 4 + -
a * b变成a b *
我们再来看 3 + 4 * 5 如何用后缀表示:
-
根据优先级,我们必须先算
4 * 5,它变成4 5 *。 -
现在,原表达式变成了计算
3加上(4 5 *)这个结果。 -
将加号
+放到后面,得到最终结果:3 4 5 * +
后缀表达式的魔力(计算机如何处理它): 计算机拿到 3 4 5 * + 后,会这样做:
-
准备一个空的地方(其实就是栈)用来放数字。
-
从左到右扫描表达式:
-
遇到
3:是数字,放进栈。栈:[3] -
遇到
4:是数字,放进栈。栈:[3, 4] -
遇到
5:是数字,放进栈。栈:[3, 4, 5] -
遇到
*:是操作符!从栈里弹出两个数字(5和4),计算4 * 5 = 20,然后把结果20再放回栈。栈:[3, 20] -
遇到
+:是操作符!从栈里弹出两个数字(20和3),计算3 + 20 = 23,然后把结果23再放回栈。栈:[23]
-
-
表达式扫描完毕。栈里剩下的唯一一个数字,就是最终结果。
后缀表达式的结构完全消除了括号和优先级规则。它的运算顺序是唯一的、内嵌的。计算机只需要一个简单的从左到右的扫描和一个栈,就能高效地完成计算。因此,它也被称为逆波兰表示法 (Reverse Polish Notation, RPN)。
前缀表达式 (Prefix Notation)
核心思想: 将操作符放到两个操作数的前面。
-
3 + 4变成+ 3 4 -
a * b变成* a b -
3 + 4 * 5变成+ 3 * 4 5
它的计算过程与后缀类似,但通常是从右向左扫描。它同样消除了括号和优先级。它也被称为波兰表示法 (Polish Notation, PN)。
三种表达式的对比与用途
| 特性 | 中缀表达式 (Infix) | 后缀表达式 (Postfix/RPN) | 前缀表达式 (Prefix/PN) |
|---|---|---|---|
| 位置 | 操作符在操作数中间 | 操作符在操作数后面 | 操作符在操作数前面 |
| 人类可读性 | 高 | 低 | 低 |
| 计算机处理 | 复杂,需处理优先级和括号 | 简单高效,通常用栈实现 | 简单高效,通常用栈实现 |
| 明确性 | 有歧义(需额外规则) | 无歧义 | 无歧义 |
| 主要用途 | 人类日常书写和阅读 | 编译器和解释器(如JVM)、计算器、栈式编程语言(如Forth) | LISP等函数式编程语言 |
手动转换(Manual Conversion)
我们把用户输入的中缀表达式,转换成计算机擅长处理的后缀(或前缀)表达式,这个过程叫做编译或解析。它是一个“翻译”工作,目的是消除歧义,提升计算机的处理效率。
现在我们来推导手动转换的规则。我们需要一个最终的后缀表达式结果,和一个临时的“操作符中转站”(这个中转站其实就是个栈)。
我们以 a + b * c - (d + e) 为例。
1. 遇到操作数(operand)(a, b, c, d, e)
-
在后缀表达式中,操作数的相对顺序和中缀表达式中完全一样。
-
规则: 遇到操作数,直接输出到结果中。
2. 遇到操作符(operator)(+, *, -, /)
-
这是最复杂的部分,我们需要处理优先级。我们用“中转站”(栈)来暂存操作符。
-
情景A:中转站是空的,或栈顶是
(-
没有比它更早的操作符,或它是一个新子表达式的开始。直接把它放进中转站。
-
-
情景B:中转站里已经有操作符了
-
假设中转站栈顶是
op1,新来的操作符是op2。 -
如果
op2的优先级 >op1的优先级 (例如,*>+)-
op2对应的运算应该先于op1的运算。就像a+b*c,*应该先算。所以,我们让op2“插队”,把它也压入中转站,等待它的第二个操作数。 -
规则: 新操作符优先级高于栈顶操作符,则入栈。
-
-
如果
op2的优先级 <=op1的优先级 (例如,+<=*,或+<=+)-
op1对应的运算应该先算或至少不比op2晚。就像a*b+c,*必须先算。所以,我们不能把op2直接压进去。我们必须把中转站里优先级更高或相等的op1先“请”出来,输出到结果中,表示op1的运算先完成。 -
规则: 新操作符优先级低于或等于栈顶操作符,则将栈顶操作符弹出并输出,然后重复此过程,直到新操作符可以入栈或栈为空。
-
-
3. 遇到括号
-
遇到左括号
(-
左括号标志着一个高优先级的子区域的开始。它会无视任何已有的操作符优先级。
-
规则: 遇到
(,直接压入中转站。它将成为这个子区域的一个“边界墙”。
-
-
遇到右括号
)-
右括号意味着一个子区域的结束。中转站里,从最近的那个
(开始的所有操作符,都必须在这个子区域内完成计算。 -
规则: 遇到
),将中转站里的操作符依次弹出并输出,直到遇到(为止。最后,将这个(也从栈中弹出并丢弃(因为它只起标记作用,不是运算的一部分)。
-
4. 遇到字符串末尾
-
整个表达式都看完了,但中转站里可能还剩下一些操作符。
-
规则: 将中转站(栈)里剩余的所有操作符,依次弹出并输出。

手动转换示例:a + b * c - (d + e)
| 当前字符 | 操作符中转站(栈) | 后缀表达式结果 | 解释 |
a | [] | a | 操作数,直接输出 |
+ | [+] | a | 栈空,+ 入栈 |
b | [+] | a b | 操作数,直接输出 |
* | [+, *] | a b | * 优先级高于 +,入栈 |
c | [+, *] | a b c | 操作数,直接输出 |
- | [ - ] | a b c * + | - 优先级低于 *,弹出*;-优先级等于+,弹出+;然后-入栈。 |
( | [-, (] | a b c * + | ( 直接入栈 |
d | [-, (] | a b c * + d | 操作数,直接输出 |
+ | [-, (, +] | a b c * + d | 栈顶是 (,+直接入栈 |
e | [-, (, +] | a b c * + d e | 操作数,直接输出 |
) | [ - ] | a b c * + d e + | 遇到),弹出+并输出,直到遇到(, 并丢弃( |
| 末尾 | [] | a b c * + d e + - | 字符串结束,弹出栈中剩余的- |
最终结果:a b c * + d e + -
未完待续…………
