day49 力扣42. 接雨水 力扣84.柱状图中最大的矩形

接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

首先我们使用单调栈求解，就要横向求解，也就是每次计算雨水面积时，都是一行一行算的。

那如何计算呢？首先我们遍历的元素大于栈顶元素时，我们保留栈顶元素，弹出，在栈里找到比这个栈顶大的元素，(这里我们只需要判断保留的那个栈顶元素的左边第一个元素是否高于栈顶元素即可，如果左边的那个元素不高于栈顶元素的话，不处理即可)高度乘宽度得面积。可以理解为 ：如果想要盛雨水，那就要有俩个边和一个底，当前遍历元素就是右边，栈顶为底，再从栈里找到的元素为左边。

注意在计算面积时，高度计算要从俩边中找到最小值，减去栈顶元素的高度；宽度计算要右边索引减去左边索引再减去1。

因为想要盛水，就必须有3个位置，那么我们的循环就应该从索引为2开始，刚开始把0和1都放进st中。

class Solution {
public:int trap(vector<int>& height) {int result = 0;stack<int> st;st.push(0);st.push(1);for(int i = 2;i<height.size();i++){if(height[i]<=height[st.top()]){st.push(i);}else {while(!st.empty()&&height[i]>height[st.top()]){int middle = st.top();st.pop();if(!st.empty()&&height[middle]<height[st.top()]){int h = min(height[st.top()],height[i]) - height[middle];int w = i - st.top() - 1;result += h*w;}}st.push(i);}}return result;}
};

柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

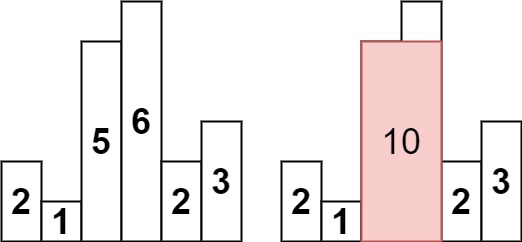
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

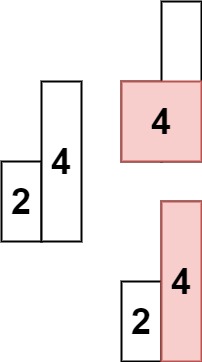
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

首先我们要知道，我们计算的是哪一个部分的面积，是我们得到的左右俩边之间的部分（不包括左边俩边），我们的middle就是高度，也是中间部分中最低的。宽度自然就是右边索引减左边索引-1。

至于为什么要找到左右俩边比middle更小的元素，是因为更小的元素就会就会限制面积的高度，如果使用的话，无法用middle作为面积的高度了。

在height的前后插入0，为防止数组单调，而无法触发计算机制。

这道题和接雨水放在一起真的会对单调栈有更深入的理解。

class Solution {
public:int largestRectangleArea(vector<int>& heights) {int result = 0;heights.insert(heights.begin(),0);heights.insert(heights.end(),0);stack<int> st;st.push(0);st.push(1);for(int i = 2;i<heights.size();i++){if(heights[i]>=heights[st.top()]){st.push(i);}else {while(!st.empty()&&heights[i]<heights[st.top()]){int middle = st.top();st.pop();int h = heights[middle];int w = i - st.top() - 1;result = max(result,h*w);}st.push(i);}}return result;}
};