C语言（06）——二、八、十、十六进制的相互转换

Hi！冒险者😎，欢迎闯入 C 语言的奇幻异世界🌌！

我是 Anklelss🧑‍💻，和你一样的闯荡者～ 这是我的冒险笔记📖，里面有踩过的坑🕳、攒的技能🌟、遇的惊喜🌈，希望能帮你少走弯路✨。

愿我们在代码山峦⛰各自攀登，顶峰碰拳👊，共赏风景呀！🥳

目录

一.初识 进制

二.进制之间的转换

2.1 二进制转十进制

2.2十进制转二进制数字

2.3 二进制转八进制

2.4 二进制转十六进制

---

一.初识 进制

在接触计算机语言之前，我就有认识到二进制这个数字的表现方式。

首先我们要对这四种进制有一个统一的认识，他们都是表现数字的一种方式，而我们日常中的123、678等用于数据计算的数字，则是应用了十进制规则。我们可以探讨同一个数字在不同进制中的表现形式，如下：

数值15的各种进制的表现形式

15的2进制：1111
15的8进制：17
15的10进制：15
15的16进制：F
//16进制的数值之前写：0x
//8进制的数值之前写:0

可能一部分读者在此之前会默认把N进制理解称为0~N的数字，但是这是不对的。

我们在十进制中进行加减法时，存在遇到10进1的规则，这就意味着在一个数位上，不可能存储下10这个数字（十进制中），故而能在一个数位上展现的数字类型就是该进制中的“有效数字”。

同时我们对十进制中的十来进行理解，十可以代表逢十进一，同样由于这个原则，我们能使用的数字范围是0~9，而这个区间内的数字总数为10，同样也对应了十进制中十的含义。由此我们也可以得出二进制中的数字范围是0~1，八进制中的数字范围是0~7，那么十六进制中是0~15么？我们可以思考这么一个问题，假设有一十六进制的数字为114，那么我们理解他的方式是1 1 4？11 4？ 还是1 14？故而为了避免这种歧义产生，10~15分别使用a、b、c、d、e、f来表示。

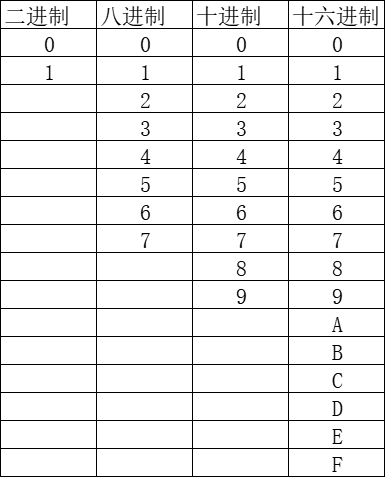
二.进制之间的转换

接下来我们以二进制为出发点了解通用的进制转换的方法。

2.1 二进制转十进制

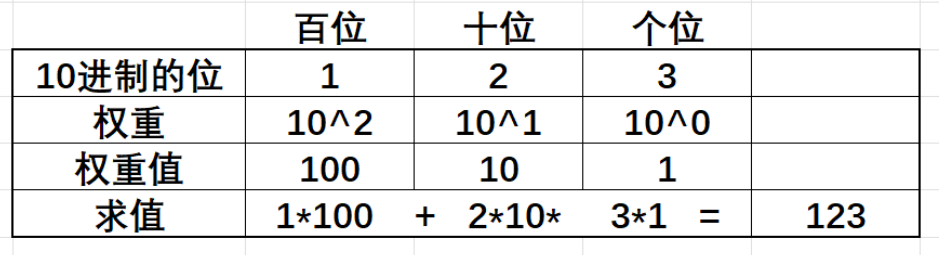
在十进制中,一个数如123，我们会说1在百位上，3在个位上。这种认知的理解就反映出了每一数位的权重关系，而权重关系就是我们理解进制转换的关键道具。

如下图：

那么我们也可以合理推测二进制的转换方式，每一位的权重从右往左依次是：

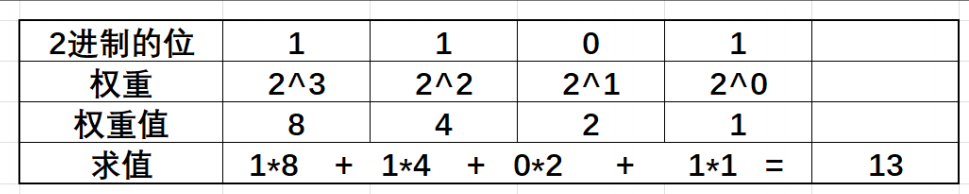
这种计算方法对于任何进制转换为十进制数字都是有效的。

2.2十进制转二进制数字

以上的方法叫做除二取余法，他的核心依据是：任何一个十进制整数 N 都可以唯一地表示成二进制数的形式，即

在使用除二取余法时，每次用十进制数除以 2 ，得到的余数就是二进制数对应位上的数字（an） 。这是因为，除以 2 得到的余数反映了该数在二进制表示中最低位的情况，而商则是去掉最低位后剩下的部分，继续对商进行除 2 操作，就可以依次确定二进制数从低位到高位的每一位数字。

2.3 二进制转八进制

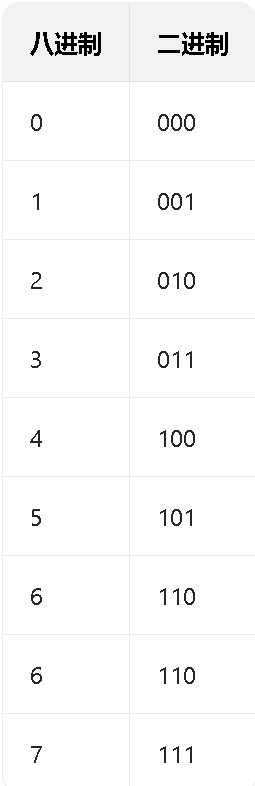
8进制的数字每⼀位是0~7的，0~7的数字，各自写成2进制，最多有3个2进制位就足够了，比如7的二进制是111，所以在2进制转8进制数的时候，从2进制序列中右边低位开始向左每3个2进制位会换算一个8进制位，剩余不够3个2进制位的直接换算。

如：2进制的 01101011，换成8进制：0153，0开头的数字，会被当做8进制。

2.4 二进制转十六进制

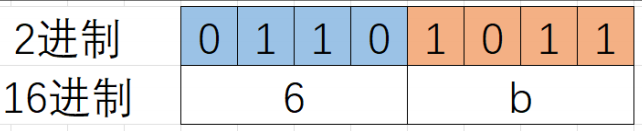
16进制的数字每⼀位是0~9, a~f 的，0~9, a~f的数字，各自写成2进制，最多有4个2进制位就足够了，比如 f 的二进制是1111，所以在2进制转16进制数的时候，从2进制序列中右边低位开始向左每4个2进制位会换算⼀个16进制位，剩余不够4个二进制位的直接换算。

如：2进制的01101011，换成16进制：0x6b，16进制表示的时候前面加0x

认识了进制之后，我们就可以更加了解认知原反补的知识框架：C语言（07）——原码 补码 反码 （超绝详细解释）-CSDN博客

后续会根据知识的增长逐步进行补充内容，也辛苦大家不吝赐教，三克油。

打怪升级中...............................................................................................................................................