Mining of Real-world Hypergraphs part1-2 逐字翻译解读

链接：https://www.youtube.com/watch?v=0mD7zOBx10M
Mining of Real-world Hypergraphs: Concepts, Patterns, and Generators (Tutorial) (Full)
PART1-2逐字翻译解读

• 节点（Node）
• 超边（Hyperedge）
• 超图（Hypergraph）
• 子超图（Sub-hypergraph）
  

  文章目录

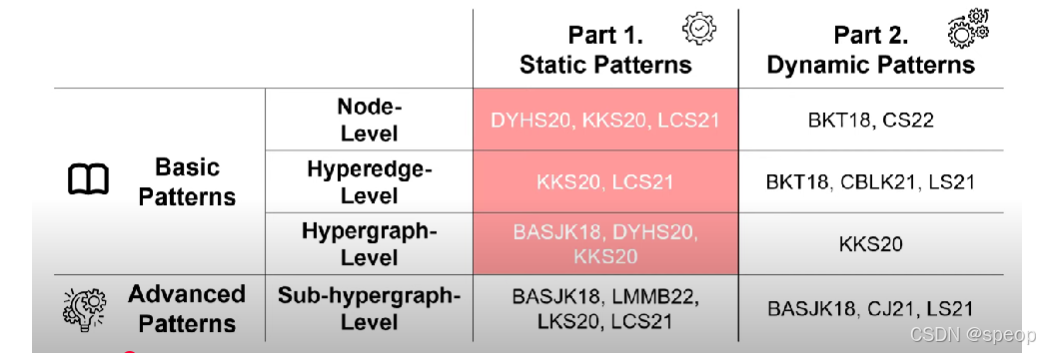
  • • part1 Static Structural Patterns
    • part2 Static Structural Patterns
    • 高级静态模式
  • 奇异值
  • • • 定义与计算
      • 几何意义
      • 与矩阵性质的关系
      • 实际应用场景
  • 交叉熵
  • • • 信息论中的定义
      • 机器学习中的应用
      • 交叉熵作为损失函数的优势
      • 与相对熵（KL散度）的关系
  • 局部聚类系数
  • • • 一、局部聚类系数（以节点 \( u \) 为例）
      • • 计算逻辑：
        • 结合例子理解（节点 \( u \) 有 5 个邻居）：
      • 二、图的聚类系数
      • 总结

part1 Static Structural Patterns

超图对个体或对象之间的群体交互进行建模。

• 每条超边是任意数量节点的子集。
• 每条超边表示其成员之间的一次群体交互。

图的局限性：
图只能通过边对 pairwise（成对的）关系进行建模。
示例：共同著作关系
通常做法是将群体中的每一对连接起来，形成一个全连接图/团/clique
但这种简单简化为成对关系的做法会丢失群体信息，从右侧的图中无法确定这三位作者之间是否存在群体交互

并且图中的每一对节点可能都发表了三篇独立的论文。在转换成对图的过程中存在信息丢失
三位作者每一对之间可能从未一起发表过论文

第一部分（群体信息丢失）
假设有三位作者（比如 A、B、C），他们可能存在 “三人共同参与一个项目 / 合作发论文” 的群体交互（不是简单的 A - B、A - C、B - C 两两分别交互）。
但如果用 “普通图” 建模（只画两两之间的边，把三人关系拆成 A - B、A - C、B - C 三条边），就会丢失 “三人作为一个整体的群体互动” 这个关键信息 —— 从图里只能看到 “两两有联系”，但看不出 “三人是否一起搞过事”。
第二部分（多元关联信息丢失）
再比如，A、B、C 三人可能共同参与了 3 篇论文（是三人一起合作，而非 A - B、A - C、B - C 分别合作发 3 篇）。
但如果把这种 “三人共同发论文” 的关系，强行拆成 “成对关系”（用普通图的多条边来表示），就会把 “三人合作 3 篇论文” 的整体信息，错误地变成 “两两之间分别有 3 次独立合作”，丢失了 “三人作为一个群体共同关联 3 篇论文” 的原始语义。

---

超图的优势

• 与图建模相比，超图建模往往更有成效。
  • 分类任务 [[LKS20] [FYZJG19]]
  • 排序任务 [[CR19]]
  • 链接预测任务 [[YSSY20]]
  • 异常检测任务 [[LCS22]]
• 关于建模方法的全面比较，可参考 [[TBBE21]]

---

超图的优势（续）
有些人认为群体交互可以表示为二分图，左侧节点是超图中的节点，另一侧节点是超图中的超边（Hyper edges）。通过这种建模方式群体间的交互不会丢失信息。

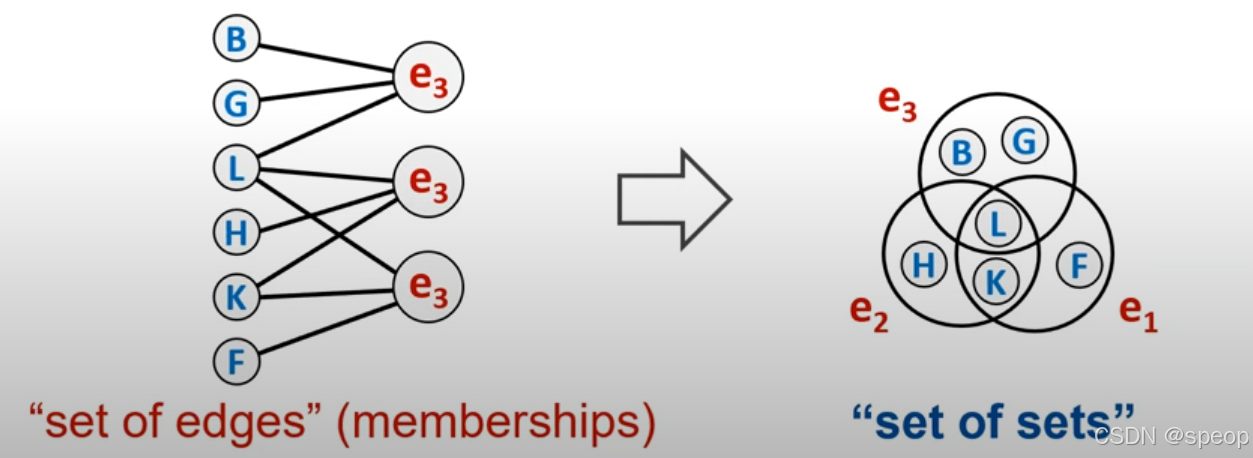
• 超图可转化为二分图（“边的集合”）。
• 然而，超图建模提供了一种新视角（“集合的集合”），并提出了一些在图（建模）中被忽视的新问题。

将群体信息建模为超图提出了一些新的问题，这些问题在图形中被忽视
超图是一组集合。


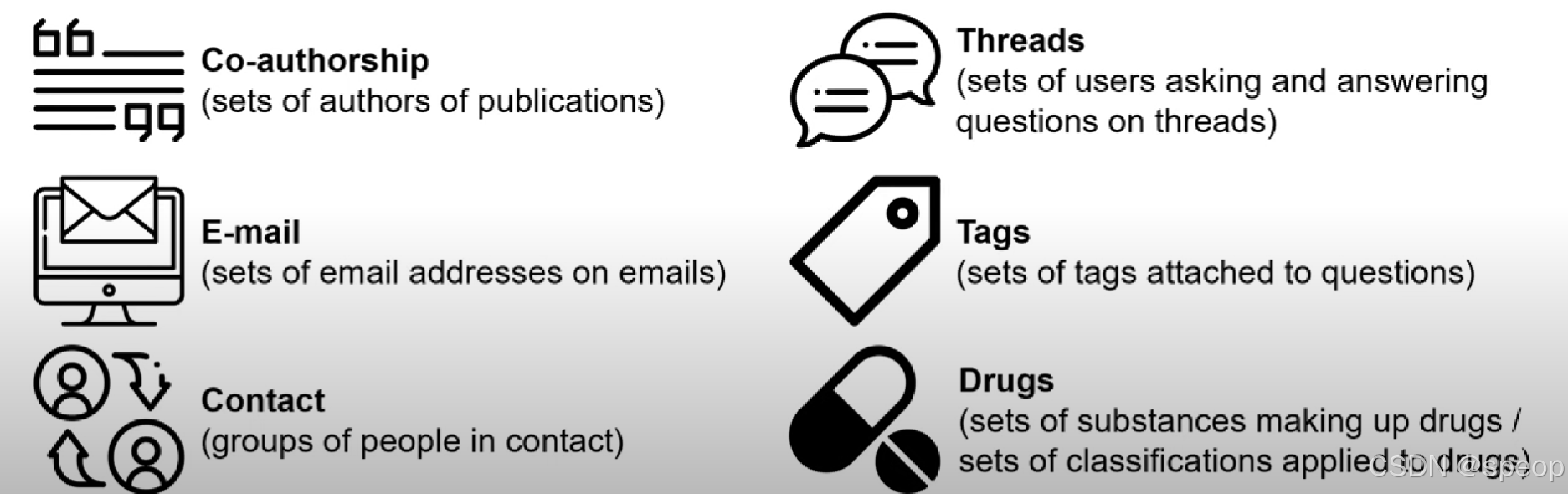
单封电子邮件邮件地址可以建模为一组超级广告

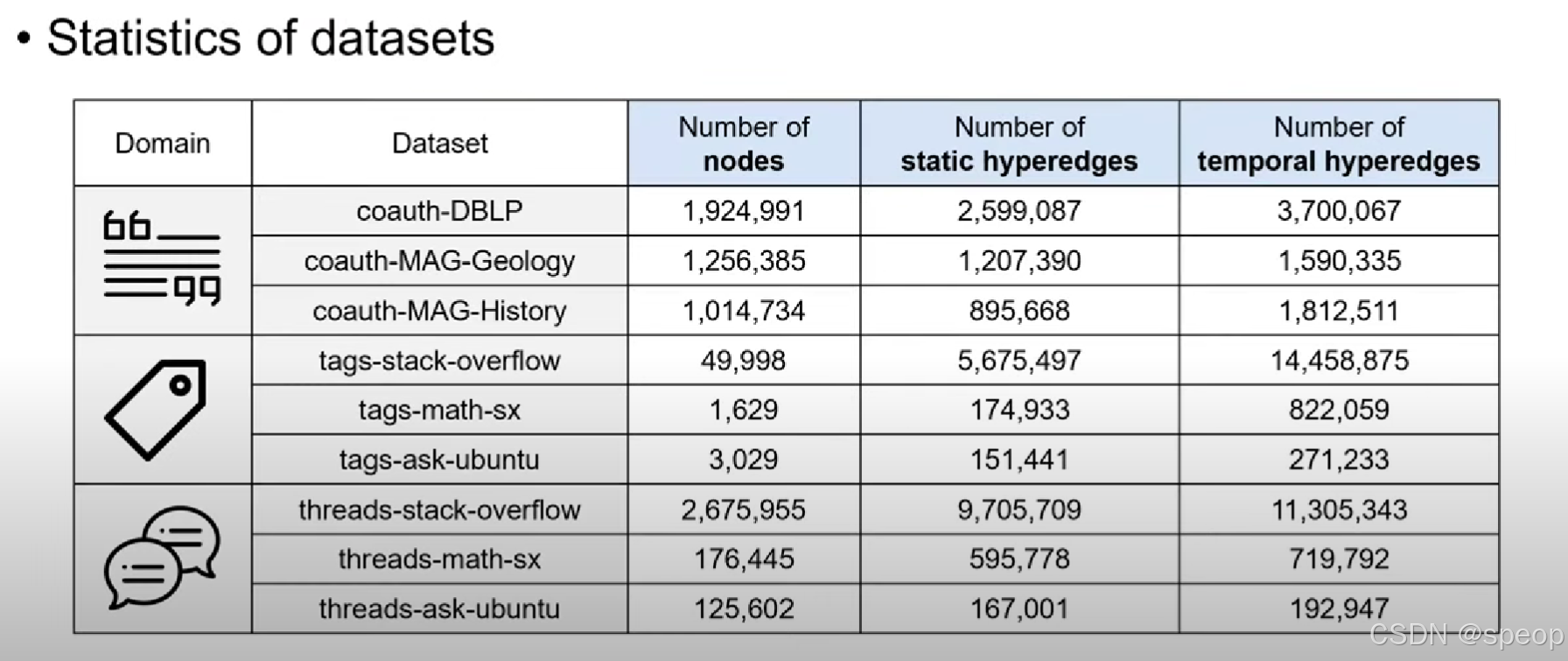
这些超图带有时间信息，每个超边到达的时间戳都是给定的
如果是静态分析，我们可以忽略这些时间信息

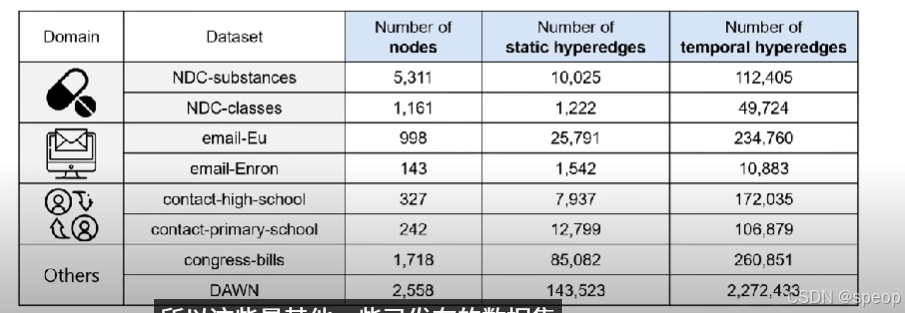
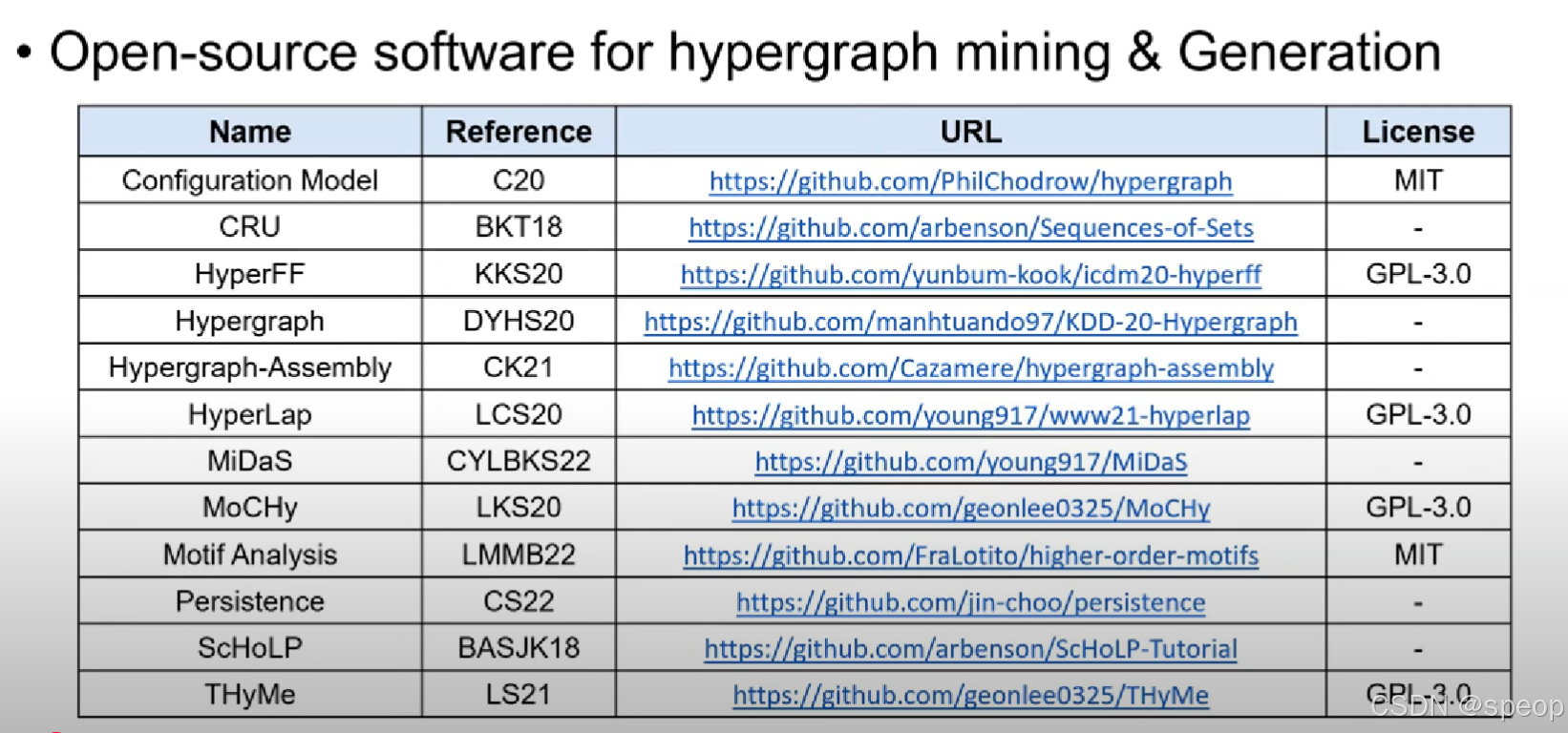
开源的超图数据挖掘和生成

路线图

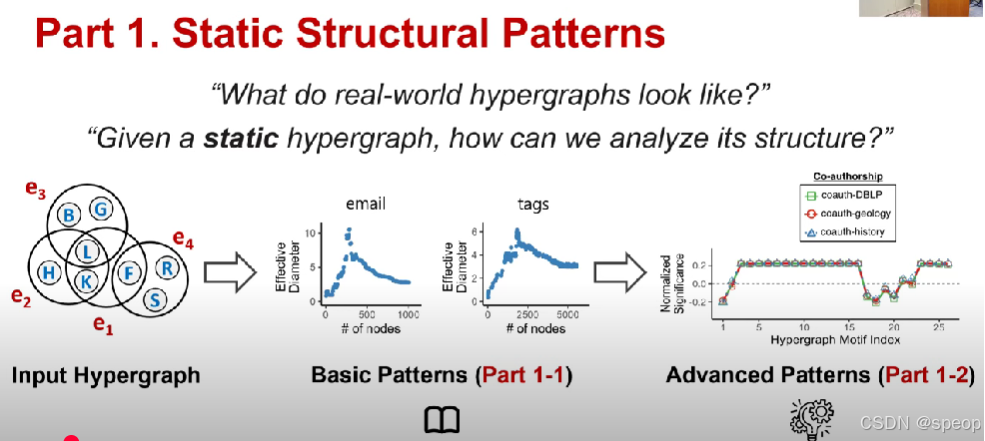
• 第一部分：静态结构模式
  • 基础模式
  • 高级模式
• 第二部分：动态结构模式
  • 基础模式
  • 高级模式
• 第三部分：生成模型
  • 静态超图生成器
  • 动态超图生成器

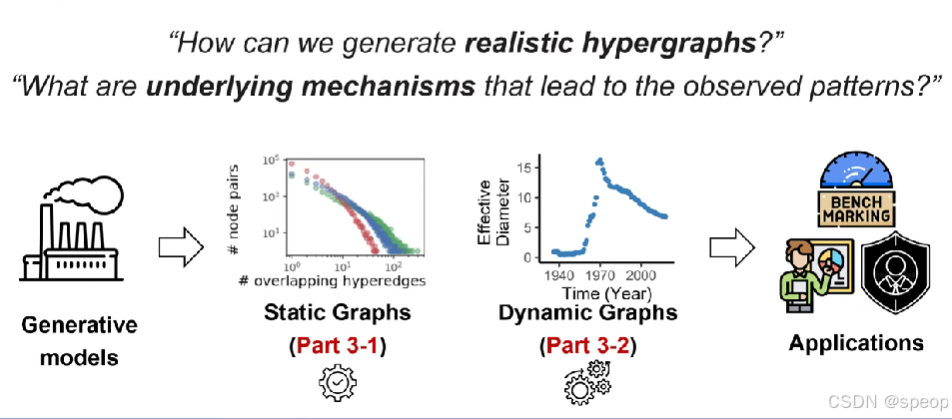
超图的生成模型：
静态模型
动态模型
还可以再分为完整的超图和子图

为什么这些很重要？

结构模式对于理解和利用超图结构数据至关重要：

• 复杂系统的预测
  • 群体交互是如何随时间演变的？
• 异常检测
  • 节点和超边是自然结构化的吗？
• 算法设计
  • 哪些结构属性可被利用来进行快速算法设计？

---

基本模式和高级模式

时间超边都会被赋予一个到达的时间戳
与静态超图不同的是，时间边由完全相同的一组节点构成。这些节点可以出现在不同的时间戳中。
而这里说的 “时间边”（带有时间属性的超边），它连接的节点集合是完全一样的，但这些节点会在 ** 不同的时间点（时间戳）** 参与到这条 “时间边” 所代表的交互、关联等关系中。

在静态超图里，超边（超图里的“边”，能连接多个节点）对应的节点组是固定的，且没有时间维度的区分。

简单举个例子：比如有三个节点A、B、C，“时间边”E连接的始终是A、B、C这组节点，但E可能在时间戳t₁、t₂、t₃等不同时间，都代表A、B、C之间发生了某种群体交互（像合作、共同参与事件等）。这就体现了“节点组相同，但出现在不同时间戳”的特点，和静态超图里超边仅对应某一固定（无时间区分）的节点组关联不同。

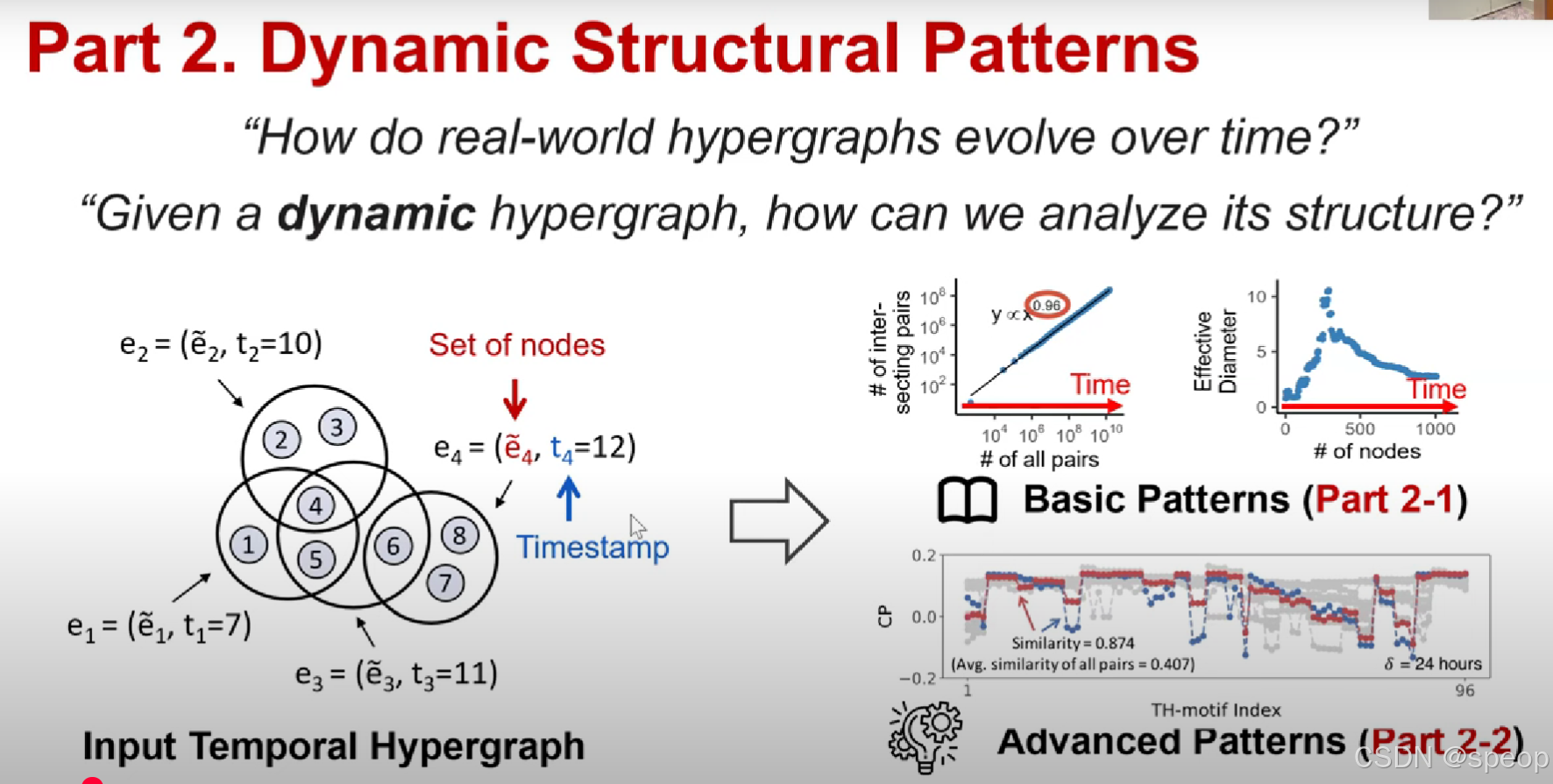
“现实世界中的超图是如何随时间演变的？”
“给定一个动态超图，我们该如何分析它的结构？”

part2 Static Structural Patterns

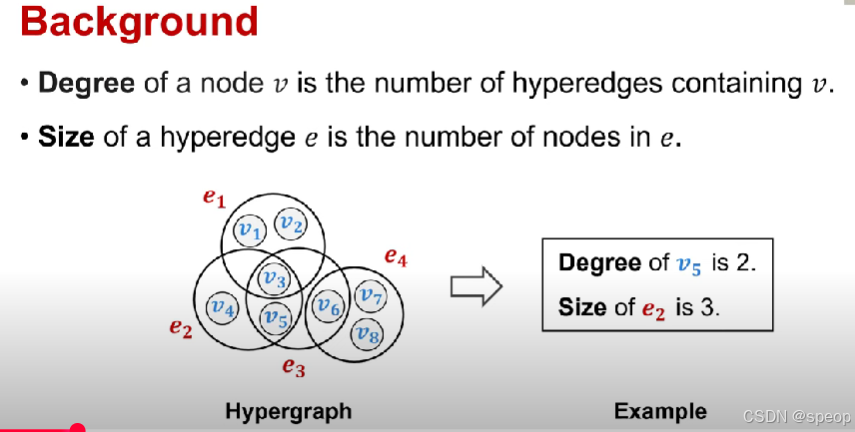
节点的度定义为包含节点的超边的数量
超边的大小e是包含数据的节点数量

“incidence matrix” 常见的释义是关联矩阵
关联矩阵是结构超图的矩阵表示形式。
换句话说，结构超图的结构可以通过关联矩阵来进行数学上的描述与表达，借助矩阵这种形式化的工具，能更方便地对超图的结构特性（比如节点与超边的关联关系等）进行分析和计算。
行表示节点，列表示超边

每个元素的值为1当且仅当它是节点时。相应的节点包含相应的超边中。
在超图中，由于超边可以是任意大小，因此我们无法准确地将超图结构表示为邻接矩阵

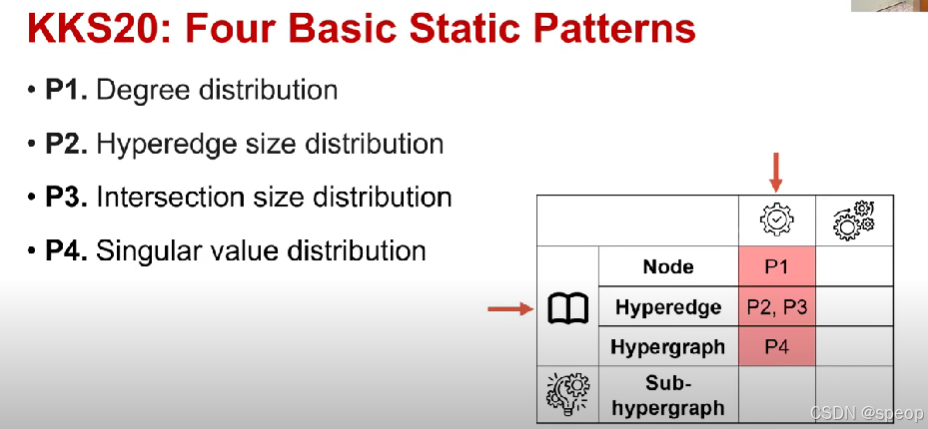
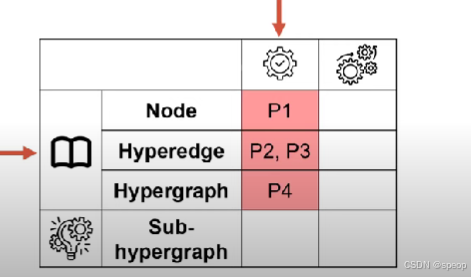
KKS20：四种基本静态模式

• P1. 度分布
• P2. 超边大小分布
• P3. 交集大小分布
• P4. 奇异值分布

istm20论文

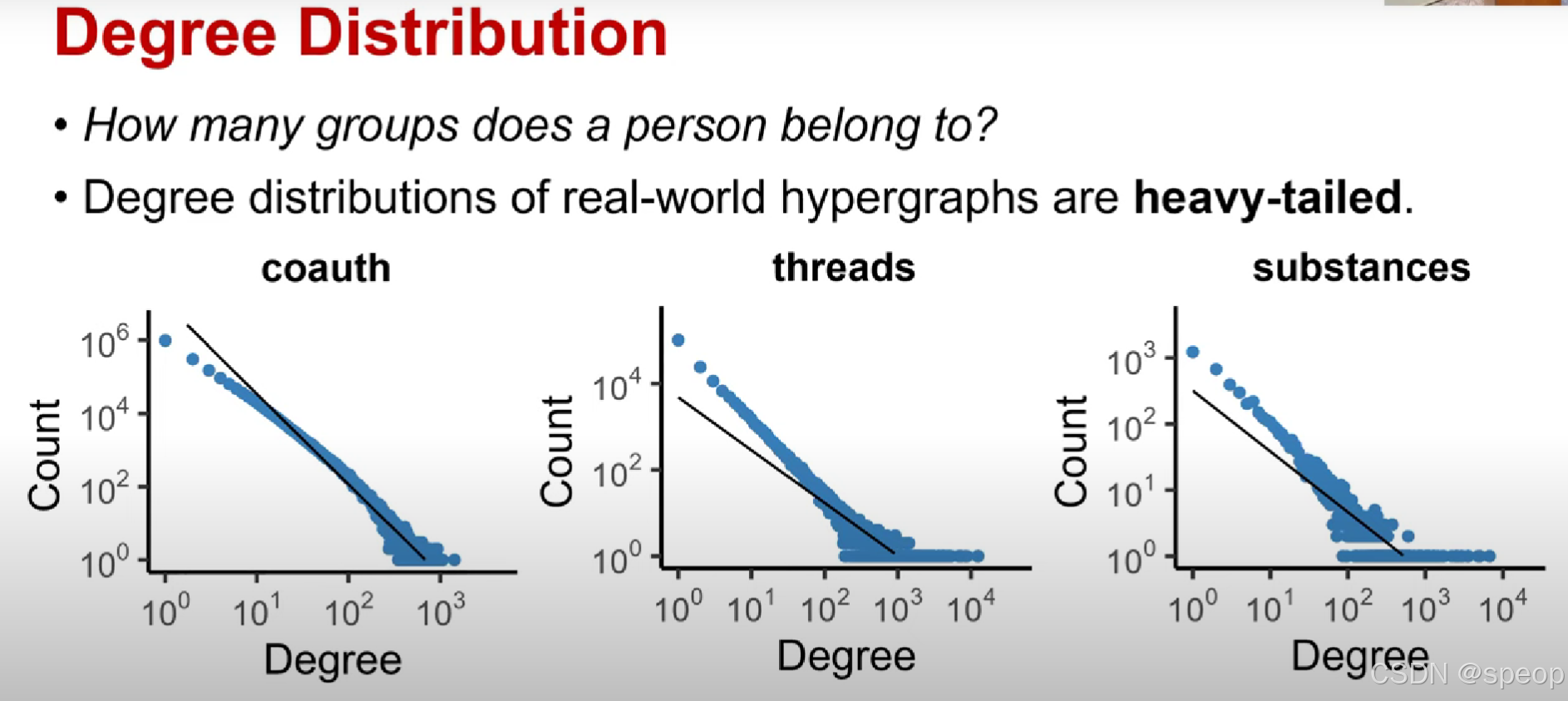
度分布

• 一个人属于多少个组？
• 现实世界中超图的度分布是重尾的。
  可以通过观察超图的度分布来回答这个问题

现实世界超图的度分布遵循幂环分布
幂环分布（power loop distribution）：一种特定的概率分布类型，可能结合了幂律（即少数元素拥有大量连接或资源，呈现 “重尾” 特征，像社交平台中少数网红有海量粉丝，多数用户粉丝量少）与环形（涉及分布在环形结构上的特性，或有周期性、环状关联的分布模式）的特点。

度数高的节点将来更有可能在未来形成组
在网络演化过程中，那些当前已经参与了很多组（度数高）的节点，在未来更倾向于与其他节点共同形成新的组（即成为新超边的成员）。

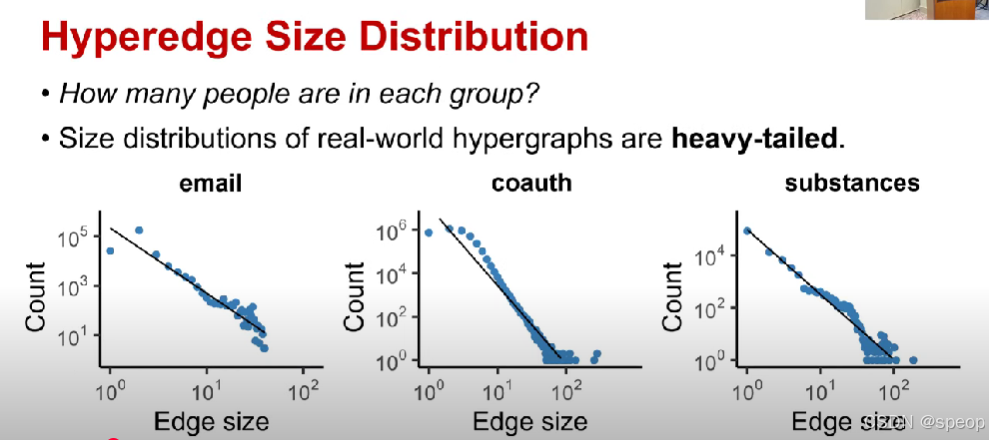
超边大小分布

• 每个组里有多少人？
• 现实世界中超图的大小分布是重尾的。
  通过观察超图大小分布来回答

超图大小分布也是遵循幂环分布的
受欢迎的组会在未来变得更受欢迎

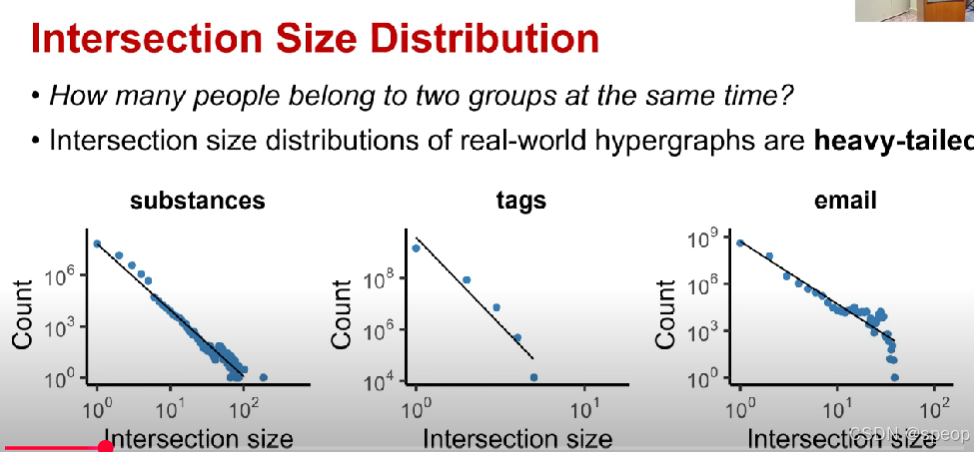
交集大小分布

• 有多少人同时属于两个组？
• 现实世界中超图的交集大小分布是重尾的。

这个问题不是观察单个超图边的大小分布，而是观察两个超图边的交集有多大
交集大小分布也是遵循幂环分布的

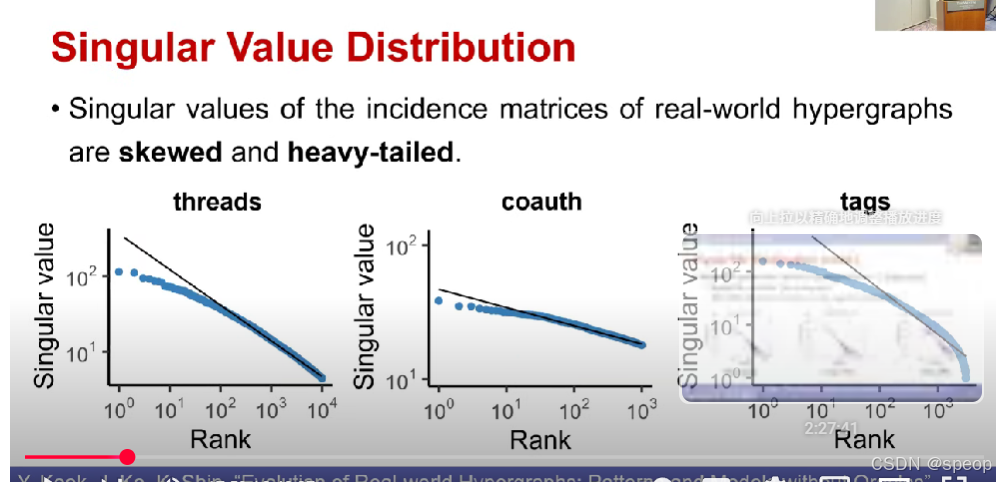
奇异值分布

• 现实世界超图关联矩阵的奇异值是有偏且重尾的。

奇异值（Singular Value）
对关联矩阵做 ** 奇异值分解（SVD）** 后，会得到一组 “奇异值”。它反映矩阵的 “能量分布”—— 大的奇异值对应矩阵中 “最核心、最具代表性的结构”。

有偏（Skewed）+ 重尾（Heavy-tailed）
有偏：奇异值的分布 “不对称”，大部分奇异值很小，只有少数奇异值很大（即 “核心结构高度集中”）。
重尾：大奇异值的 “出现概率比普通分布更高”（类似 “少数超边 / 顶点承载了绝大多数关联”，比如社交网络中少数热门社群关联了大量用户）。

---

两种基本静态模式

• P1：节点对/三元组的度分布
• P2：超边同质性分布

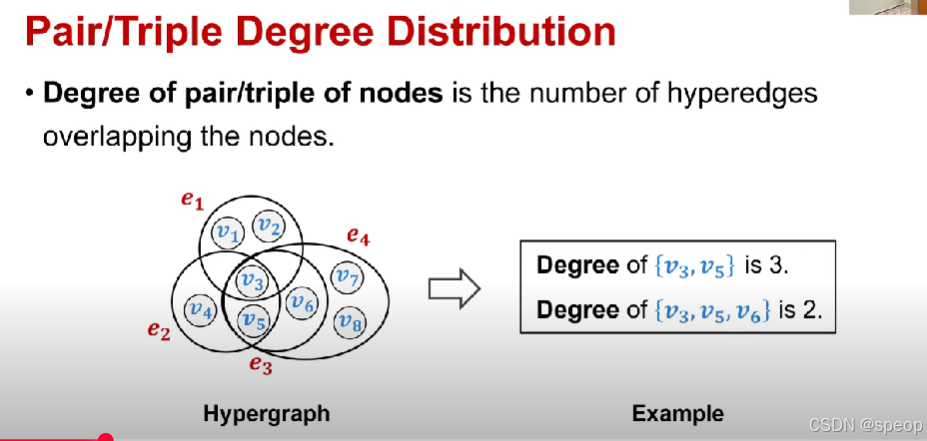
节点对/三元组的度分布是
节点对/三元组的度数是与这些节点重叠的超边数量。
节点们被共同包含的超边越多，说明它们在超图里的关联模式越像，结构相似性就越高。
如果两个或三个节点被同一条超边包含，说明它们在超图里有共同的关联（比如共同属于一个社群、共同参与一个项目等）。当它们被一起包含在更多超边中时，意味着它们在超图的结构里有更多共同的 “连接场景”，所以结构上就更相似。

---

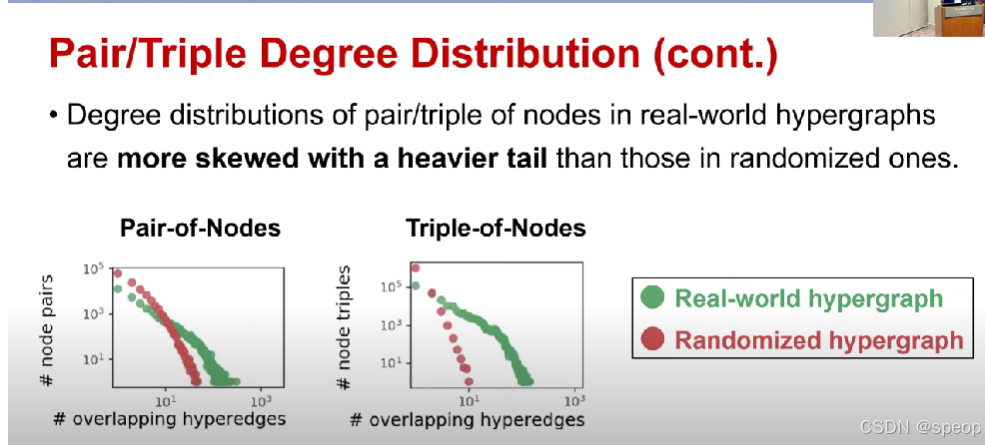
节点对/三元组的度分布（续）

• 现实世界超图中节点对/三元组的度分布，比随机超图中的度分布更有偏且重尾
  从更高维度 / 更宏观的角度，去理解节点作为集合与更高阶超边之间的关联逻辑
  让我们了解节点是如何作为一个集合从更高阶超边中（形成或产生关联的）

节点对/三重节点交互的次数越多，他们再次交互的可能性就越大

Hyperedge level pattern
超边同质性

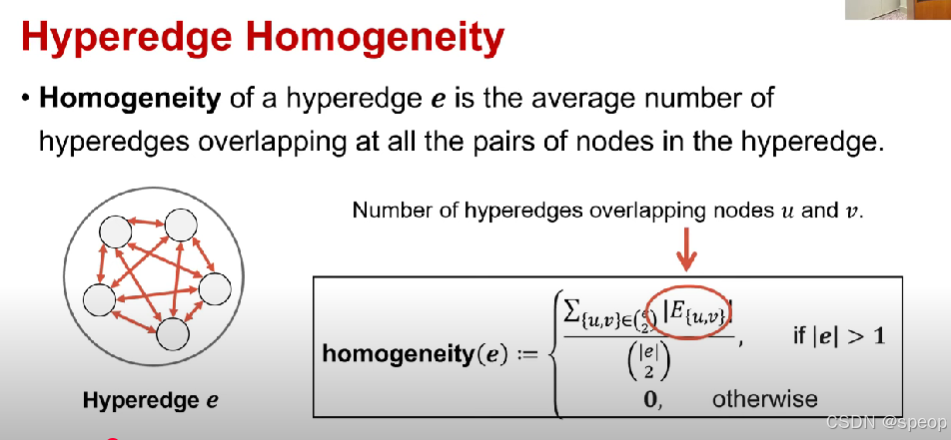
• 超边$e$的同质性是超边中所有节点对所重叠的超边数量的平均值。
  因此这可以衡量超边中的节点结构上的相似性，这个节点的数量可以增加

• 与节点 $u$ 和 $v$ 重叠的超边数量。

（公式）
homogeneity(e):={∑{u,v}∈(e2)∣E{u,v}∣(∣e∣2),若 ∣e∣>10,否则\text{homogeneity}(e) := \begin{cases} \frac{\sum_{\{u,v\} \in \binom{e}{2}} |E_{\{u,v\}}|}{\binom{|e|}{2}}, & \text{若 } |e| > 1 \\ 0, & \text{否则} \end{cases}homogeneity(e):=⎩⎨⎧​(2∣e∣​)∑{u,v}∈(2e​)​∣E{u,v}​∣​,0,​若 ∣e∣>1否则​

组成超边的节点是如何相互关联
在现实世界中超图中，超边不太可能由随机组成选择的节点。
相反，我们可以预期单个超边中的节点有很强的依赖关系

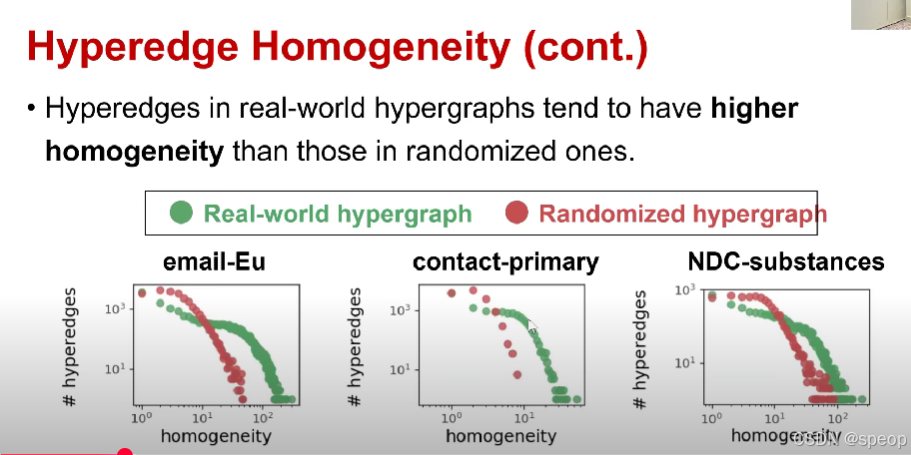
超边同质性（续）

• 现实世界超图中的超边，往往比随机超图中的超边具有更高的同质性。

下图为不同数据集的三种不同分布，是超边同质性

（图例）

• 绿色：现实世界超图
• 红色：随机超图

（子图标题依次为）

• 电子邮件 - 欧盟（email - Eu）
• 主要联系人（contact - primary）
• 国家药品代码 - 物质（NDC - substances）

对比得出现实世界中的超图比随机超图往往具有更高的同质性

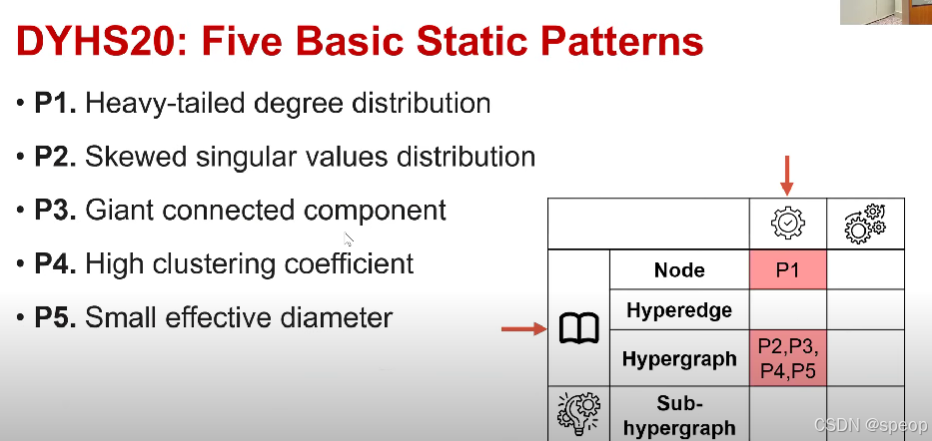
DYHS20：五种基本静态模式

• P1：重尾度分布
• P2：有偏奇异值分布
• P3： giant 连通分量（注：“giant”常表示“巨型、超大”，此处指超大规模的连通部分）
• P4：高聚类系数
• P5：小有效直径
  
  超图具有更复杂的结构，它包含普通图无法包含的某些组信息。另一个动机是挖掘图的工具比超图更多
  因此，如果我们可以将超图转换为成对图，那么我们就可以采用几十年来一直在研究的图形的各种属性或工具
  将超图转换为成对图的一种简单方法称为点击扩展（clique expansion）
  这里提到的 “投影（projection）” 也叫 “团扩展”，将超图通过团扩展（投影）的方式转换为普通图时，会存在信息丢失的问题，并且转换后的图只能体现节点层面的相互作用，无法保留超图原有的高阶信息（比如多个顶点之间复杂的关联关系）。
  团扩展是将每个超边作为团，因此它将每个超边中的每一对节点作为边成对连接
  

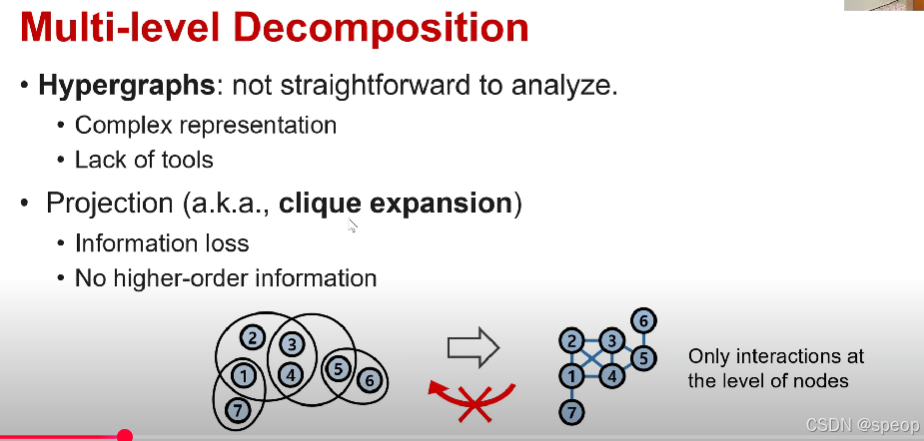
多级分解

• 超图：分析起来并不直接。
  • 复杂的表示
  • 工具匮乏
• 投影（也称为团扩展）
  • 信息丢失
  • 没有高阶信息

（下方图示：仅存在节点层面的相互作用）

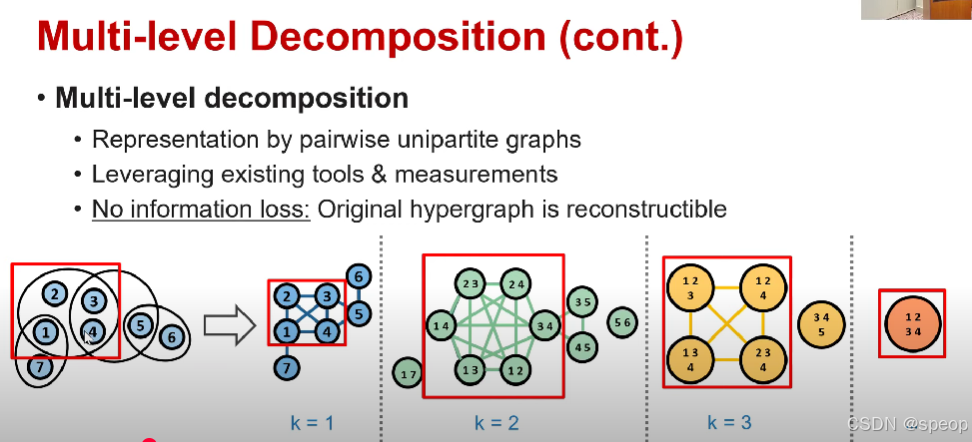
不是将超图分解成节点级别的图，而是考虑节点子集之间的成对关系
因此在超图的K级分解中，每个节点都是K个节点的子集，并且K个节点曾经共享过超边
两个节点之间的边被建立如果两个子集的并集有共享过超边
如下图第一个图的红色框，包含1，2，3，4节点。可以将其分解为多个节点子集
因此，如果K为1，则将其分解为4个单独的节点。
如果K为2，则生成6个节点($C_4^2$)。其中每个节点是两个节点的子集。
K级分级图自然表示每组K节点如何与其他组K节点交互。
使用这些分解图，我们可以利用现有的度量和工具进行图分析。
多边分解的另一个优点是没有信息丢失。从右侧的分解图，我们可以完全恢复下标图的组信息。
从右侧的分解图中，我们可以完全恢复超图的组信息【论文中可以找到这个证据】

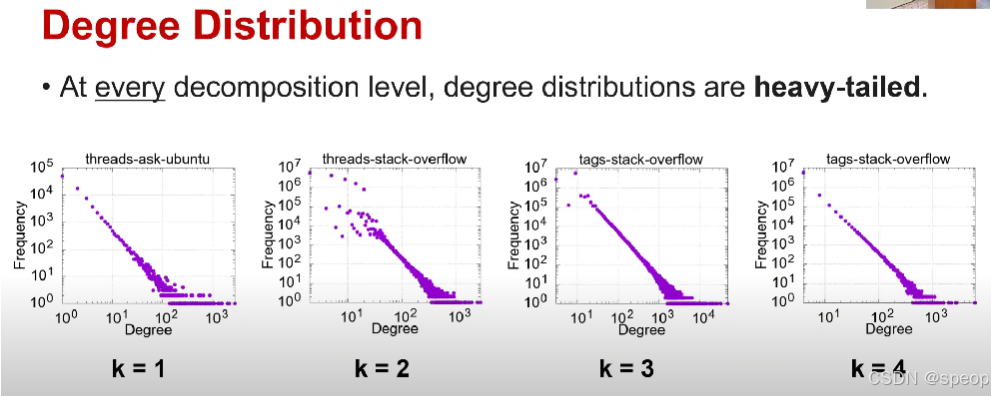
度数分布

• 在每一个分解层级，度数分布都是重尾的。
  富者更富的趋势不仅在节点级别的分解图中观察到，而且在节点级别的子集中也可以观察到
  因此高阶子集更有可能与其他节点子集交互

分解图侧重于通过对原图的处理来呈现原图不同的结构特征；子集侧重于从原图中抽取特定部分

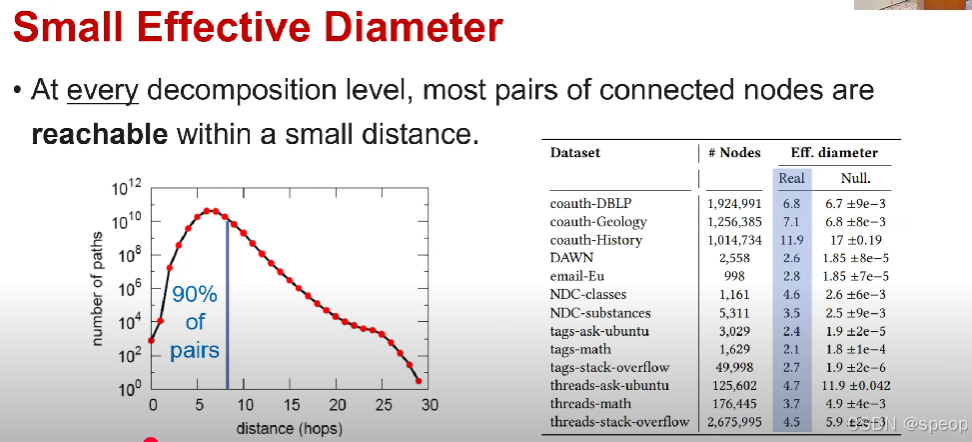
奇异值分布（由邻接矩阵或者分解图计算而来）

• 在每一个分解层级，奇异值分布都是重尾的并且有偏的。
  因此这与我们在关联矩阵计算奇异值得到的结果类似

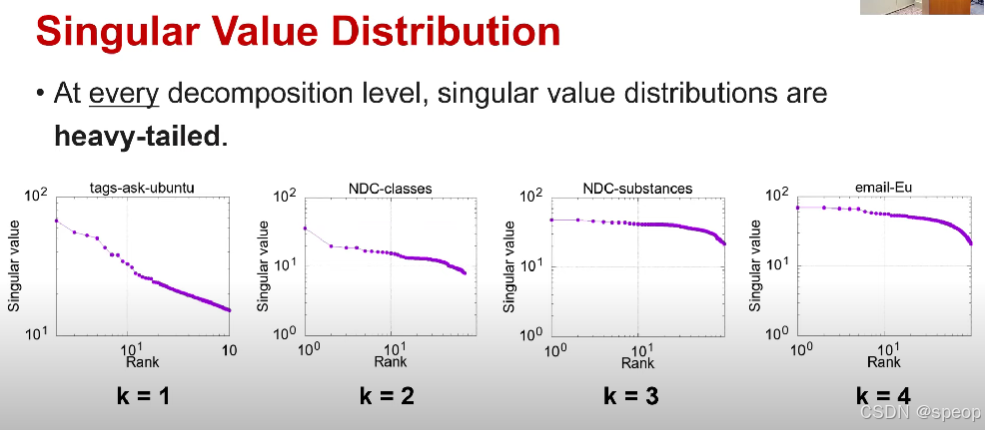
giant connected component：巨连通分量

• 很大比例的节点是相互连接的。
  接下来我们可以观察到分解图具有巨大的连通分量，这是在实际中观察到的图的属性之一
  这意味着存在一个由巨大的比例节点组成的连通分量
  针对不同的数据集和不同的分解级别 列出了节点在最大连通分量中的比例
  当K平滑的时候（如K=1），我们可以观察到该比例非常高，这意味着存在一个大连通分量。
  但是当K变大时，小于K的超边不再创建任何节点子集，因此分解图将非常稀疏。
  因此，它的连通性会降低。
  
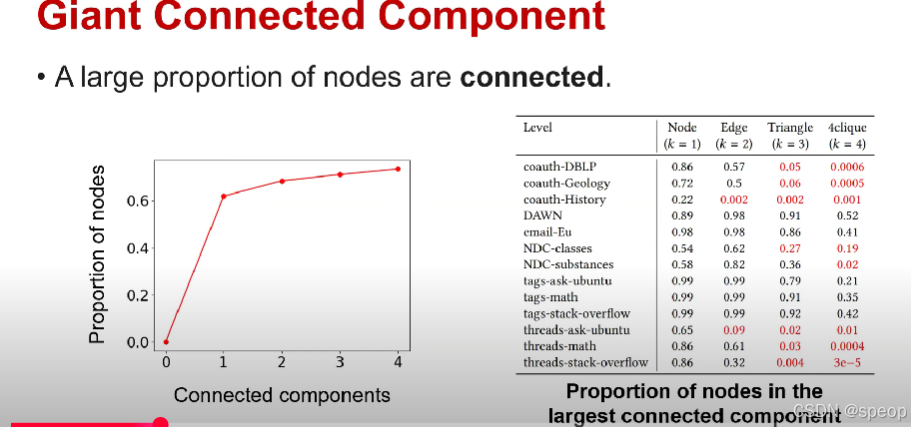
  高聚类系数
• 在每一个分解层级，“朋友的朋友”之间存在连接的可能性都很高。

节点u的局部聚类系数为$C_u=\frac{3}{10}$。
图的聚类系数为 $C=\frac{1}{|V|}{\sum }_{v\in V}{C}_v$。 vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv

节点u有5个邻居，3对邻居是连接的，而最多可以有10对连接
因此节点u的局部聚类系数将是3/10
整个图的聚类系数将是图中节点平均局部聚类系数的平均值
在右侧表格中 现实世界超图或分解图的聚类系数和随机神经图的聚类系数
与随机神经图相比，现实世界超图的聚类系数通常更高。
因此，由于聚类系数衡量，“朋友的朋友”之间存在连接的可能性。现实世界超图比神经图更具聚类性

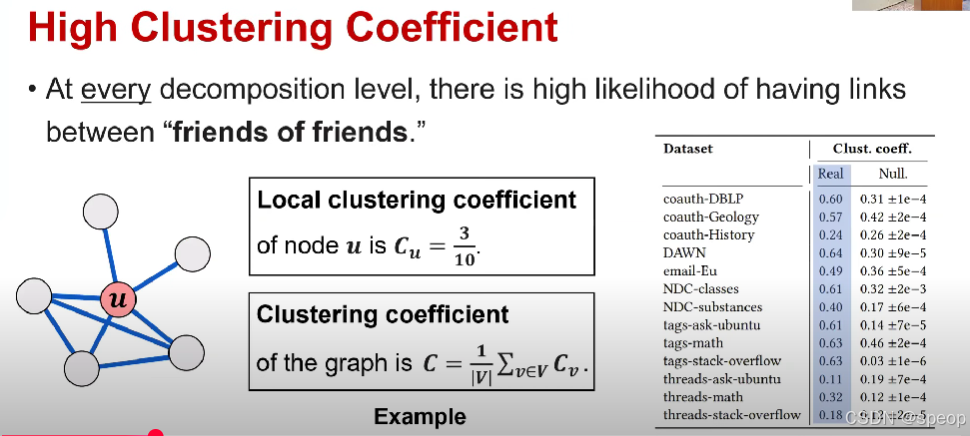
小有效直径
在每个分解层级，大多数相连节点对都能在短距离内可达。
分解图的有效直径定义为最小距离，大约90%的连接对都是可达的

高级静态模式

路线图

• 第一部分：静态结构模式
  • 基础模式
  • 高级模式<<
• 第二部分：动态结构模式
  • 基础模式
  • 高级模式
• 第三部分：生成模型
  • 静态超图生成器
  • 动态超图生成器
    

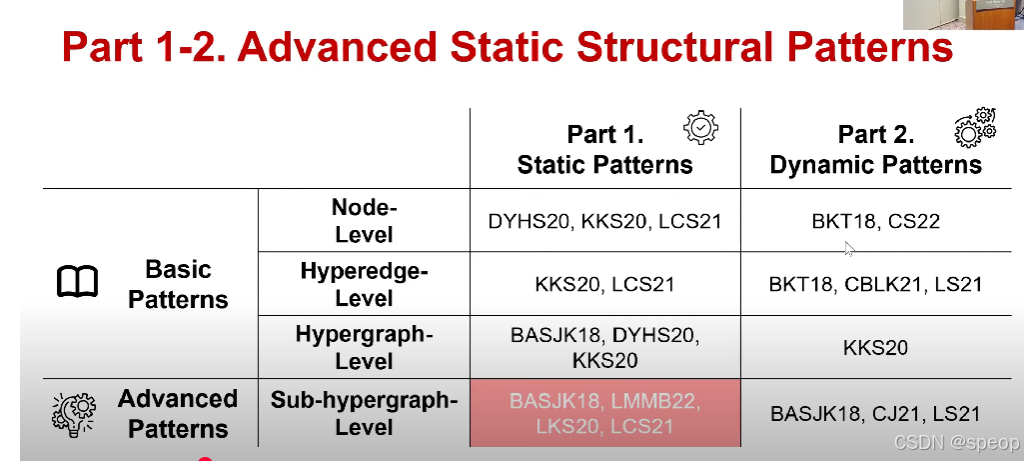
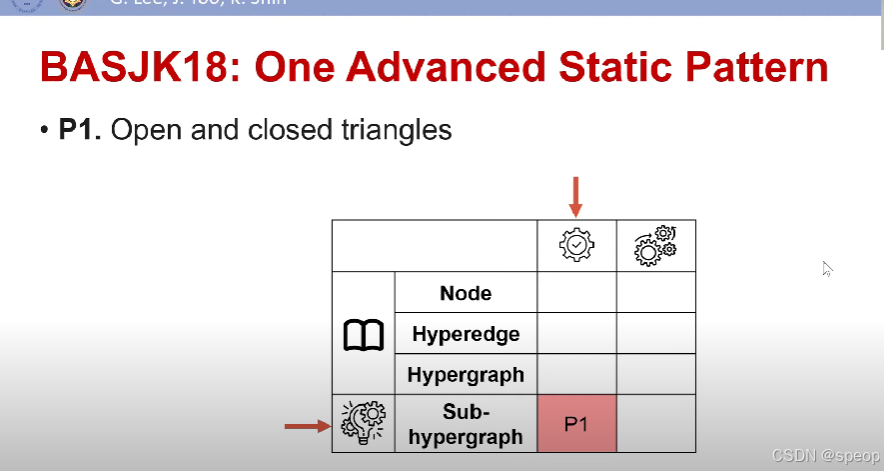
第一个高级模型是超图中的三角形，在期刊和mt19中都有介绍
背景

• 三角形是由3个节点构成的团（完全子图）。
• 三角形的数量是一个重要的基本要素/基本要素/组成部分。
  • 例如，社区检测、垃圾信息检测、链接预测。

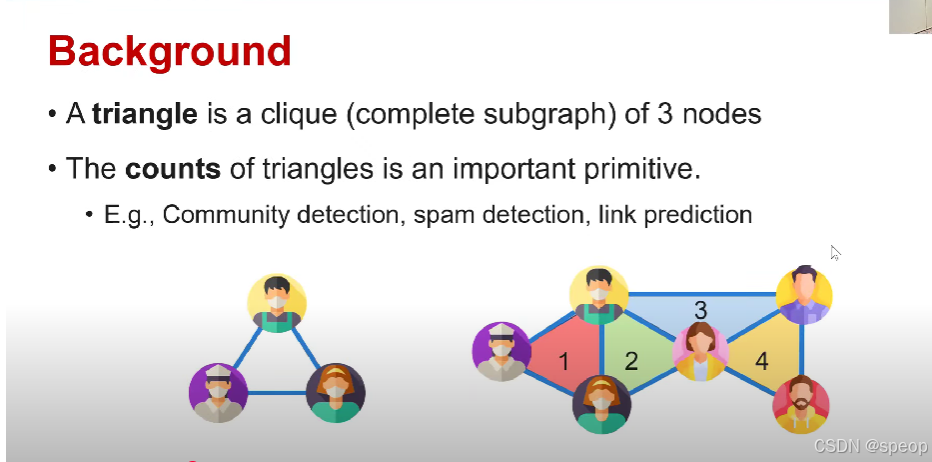
超图中的三角形
问题：
如何定义超图中的三角形？
答案：
应当考虑三元关系（即三个节点的群体交互）。
我们不仅要考虑节点之间的两两关系，还要考虑三方关系来定义超图

超图中的两种三角形
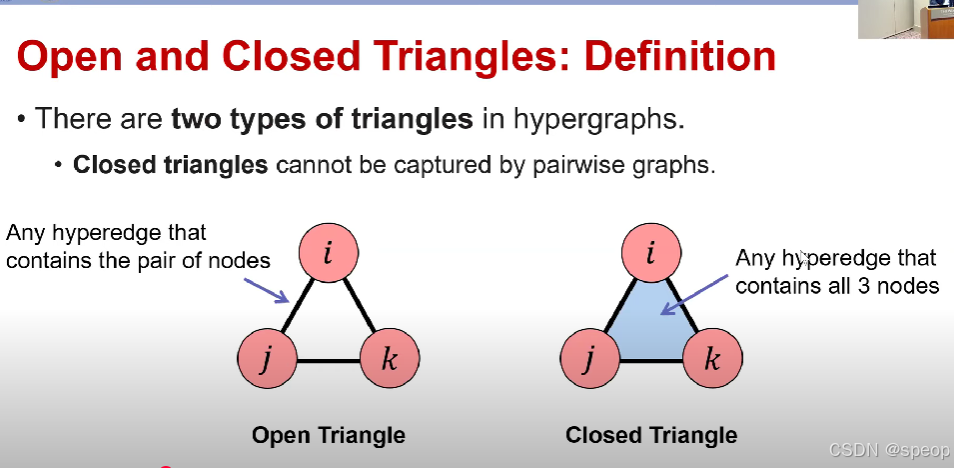
开放三角形与闭合三角形：定义

• 超图中有两种类型的三角形。
  • 闭合三角形无法被成对图捕捉。

（左侧图示）开放三角形：包含节点对的任意超边。每一对节点都在某条超边中有过共同交互。但所有三个节点从未在同一条超边中有过共同交互。
（右侧图示）闭合三角形：包含所有3个节点的任意超边。三个节点一起出现在单个超图中，因此，从定义中我们知道闭合三角形没办法通过仅考虑节点两两之间关系的图（pairwise graphs，也就是普通的二元关系图。因为它至少需要三个节点的三方关系。

下图有开放和封闭三角形的比例，以及它与其他指标的关系
在图中，x是投影图中的边密度，y是开放三角形的占比，图中的每个点代表不同的数据集，形状代表是数据集的不同域
我们可以观察到，来自同一域的数据集在途中排列紧密，这意味着三角形的比例是超图结构的有意义的度量。
跨领域的三角形

• 同一领域内，开放三角形的占比情况较为相似。
  

在这个图中每个点代表节点上的自我中心网络，节点的自我中心网络是由包含该节点的一组超边所构成的网络。
节点的自我中心网络指的是以某个特定节点为中心，包含该节点以及与该节点直接相关联的其他节点和它们之间的连接关系所构成的网络。节点的自我中心网络由包含该节点的一组超边构成。当构建以某节点为中心的自我中心网络时，就是把所有包含该节点的超边所涉及的节点及关联都纳入进来，以此形成围绕该节点的局部网络结构
（图表相关）
开放三角形的占比；决策边界；联系人；线程；标签；电子邮件；节点的自我中心网络；平均度
跨领域的三角形（续）

• 同一领域内，开放三角形的占比情况较为相似。

x轴是自我中心网络的平均度
y轴是开放三角形的占比

来自同一领域的自我中心网络排列紧密，来自不同领域的自我中心网络界限分明
开放三角形的比例有助于根据域区分自我中心网络

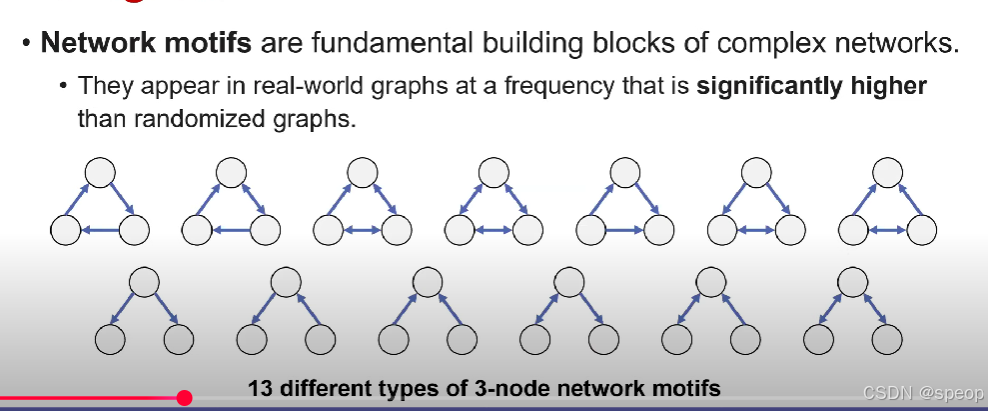
网络模体（Network motif）：是复杂网络的基本构造模块。在现实世界的图（网络）中，它们出现的频率显著高于随机图（通过随机化等方式生成的参照图）。

（下方图示）13 种不同类型的 3 节点网络模体
它通常被定义为由三、四或五个节点组成的软图模式，

“软图模式（Soft Graph Pattern ）” 相关概念多应用于图数据处理、机器学习、复杂网络分析等领域 ，是相对 “硬图模式” 而言的：
定义：软图模式允许一定程度的灵活性和不精确匹配，不要求图结构在节点、边的属性和连接关系上完全一致，而是关注图结构的相似性和近似匹配。例如，在社交网络分析中，对于 “朋友关系圈” 这种图模式，软图模式不会严格限定必须是固定数量、特定身份的朋友构成，只要结构和关系类似，就可以认为符合该模式。

如何在超图中定义更多模体呢
高阶网络基序：定义

• 高阶网络基序是网络基序的推广。
• 它们额外考虑了节点之间的群体交互。例如对于三个节点可以有六种不同的高阶网络模体。如果我们只考虑节点之间的成对关系，那么只能描述左侧的两种类型。但如果我们另外考虑群体相互作用，或者三个节点之间的三元关系，我们可以进一步将这些模式描述为六种不同类型的高阶网络模体

网络基序只能描述2种模式。

（下方图示）6种不同类型的3节点高阶基序

那么我们可以使用高阶网络模体进行什么样的分析?
给定一个超图，我们可以计算高阶网络模体出现的次数，然后我们跟随机超图对比次数
在这个图x代表六种类型的告高阶网络模体，y轴是相对于随机网络，高阶基序的丰度，如果丰度为正则意味着与随机超图相比相应的高阶网络模体在现实世界类型图中出现的次数更多。如果为负，则意味着它在随机超图中出现的次数更多。

在 “Abundance of higher - order motifs relative to random networks” 这个表述里，“abundance” 的意思是丰度；数量；多度。它用于描述高阶基序在与随机网络对比时，出现的数量情况或者丰富程度。
作者从四个不同的领域进行了对比，不同高阶网络模体在每个领域都有突出显示
从这个图可以分析哪种模体是高阶网络模体，哪种局部结构对它们构建每个超图很重要

计算每个超图中出现的高阶网络模体的实例数。我们可以构建一个六维向量
每个元素代表高阶网络模体在超图中出现的次数，我们可以对比两个不同超图的六维向量之间的相关系数，例如皮尔逊相关系数。
相关性将表明两个超图的局部结构的相似程度。
此热图表示每对数据集和每个测试的相关性，其范围在-1到1之间。
左侧legend是属于四个域之一的 它在 Hitman 的左侧以颜色显示。
来自同一域的模体之间的相关性非常高不同域的相关性非常低。这意味高阶网络模体可以有效地表征超图的局部结构

以前的高阶网络模体是由固定数量节点的子图模式定义的，通常我们将高阶网络模体定义为三个连接节点的模式
但在超图模体中描述的是 三条相连超边的连接模式，而不是节点。每个模体基于七个子集是否为空来描述连接模式，
空性意味着子集是否存在任意数量的节点？

如图三个超边可以构建七个不同的子集
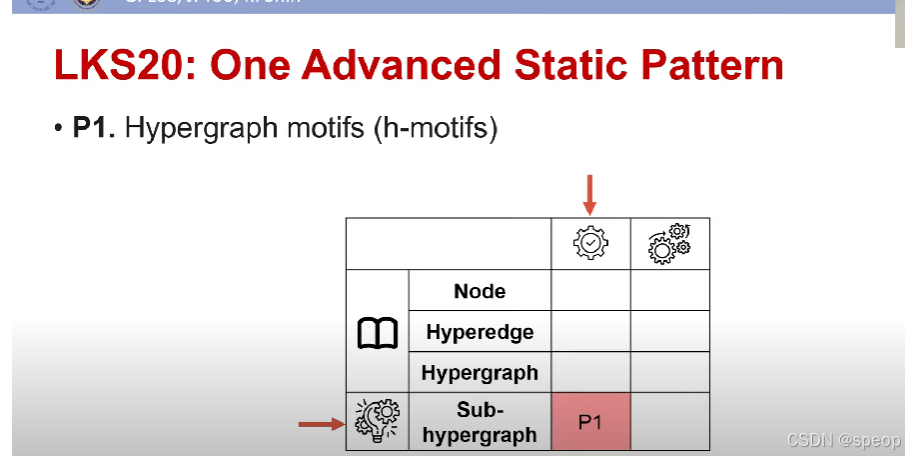
超图基序：定义

• 超图基序（h - 基序）描述了三条相连超边的连接模式。
• 超图基序通过七个子集$（1）-（7）$是否为空，来描述超边 $e_i$、$e_j$ 和$e_k$ 的连接模式。
  

---

因为有七个不同的子集，所以最多可以存在128种不同的情况
超图基序：定义（续）

• 虽然可能存在 $2^7$ 种超图基序，但排除以下情况后，还剩 26 种超图基序：
  1. 对称的超图基序 (ei,ej)<->(ej,ei)
  2. 无法从不同超边得到的超图基序 超图基序得是由不同的超边组合出来的有意义结构，如果某个 “基序” 没法通过 “不同的超边” 来形成，那它不符合实际超图里的结构逻辑，就排除。，假设要形成某个基序，需要超边 e1,e1,e2 重复了，不是不同的超边），这种情况下，这个 “基序” 就属于 “无法从不同超边得到”，因为它依赖于 “重复的超边”，而非真正不同的超边之间的交互，所以会被排除。
  3. 无法从相连超边得到的超图基序 超图基序描述的是 “相连超边” 的连接模式，要是某个 “基序” 没法从 “相互连接的超边” 里产生，那它也不符合超图基序的定义，所以排除。超边 ei连接节点A、B、C ，超边ej 连接节点D、E、F超边ek 连接节点G、H、I ，这三个超边之间完全没交集（节点、连接上都不重叠），是孤立的。如果某个 “基序” 需要这三个孤立的超边来构成，那它就属于 “无法从相连超边得到”，因为超图基序关注的是 “相连超边” 的模式，孤立超边的组合不符合这个核心，所以会被排除。
     有色子集表示基底非空，所以存在任意数量的节点。非彩色子集表示子集为空
     
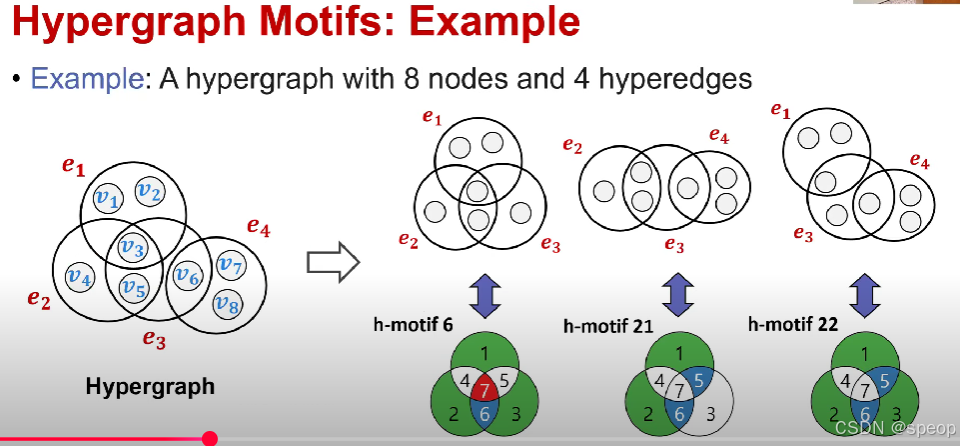
     超图基序：示例
• 示例：一个包含8个节点和4条超边的超图，从该超图中我们可以找到一些h模体的实例。超图中的超边e1,e2,e3是连接的。因此，这将是超图模体的实例。我们可以在下面看到七个子集的空性，这对应于H模体为6。

超图模体有三个重要的属性
超图基序：性质

• 完备性：超图模体（h - 模体）捕捉所有可能的三条相连超边的连接模式。意味着超图里只要是三条相互连接的超边，它们之间的连接模式（也就是超边之间通过节点等形成的关联结构方式），一定能对应到之前提到的那 26 种超图基序（h - 基序）中的某一种。
• 唯一性：对于超图中任意三条相互连接的超边，它们之间的连接模式（也就是超边之间通过节点等形成的关联结构方式），只会对应且仅对应一种超图基序（h - 基序）。
• 尺寸无关性【重要】：超图模体捕捉连接模式时，与超边的尺寸无关。超图模体在描述超边之间的连接模式时，不考虑超边本身包含的节点数量多少。
  超图中超边大小的灵活性是超图非常重要的属性之一
  

超图模体：性质（续）

• 问题： 为什么要考虑非成对关系？
• 答案： 非成对关系在捕捉现实世界超图的局部结构模式方面起着关键作用。
• 例如，{e2,e3,e4}\{e_2, e_3, e_4\}{e2​,e3​,e4​} 和 {e1,e3,e4}\{e_1, e_3, e_4\}{e1​,e3​,e4​} 具有相同的成对对关系，但它们的连接模式可通过超图模体（h - 模体）来区分。

特征概貌

• 问题： 我们如何总结超图的超图模体（h - 模体）性质？
• 答案： 我们计算每个超图模体的归一化显著性的紧凑向量。
  为了比较不同大小的超图的局部结构，我们需要有一个与超图大小无关的代表性向量
  我们计算一个26维紧凑模式，每个元素都是每个H模体的归一化重要性
  

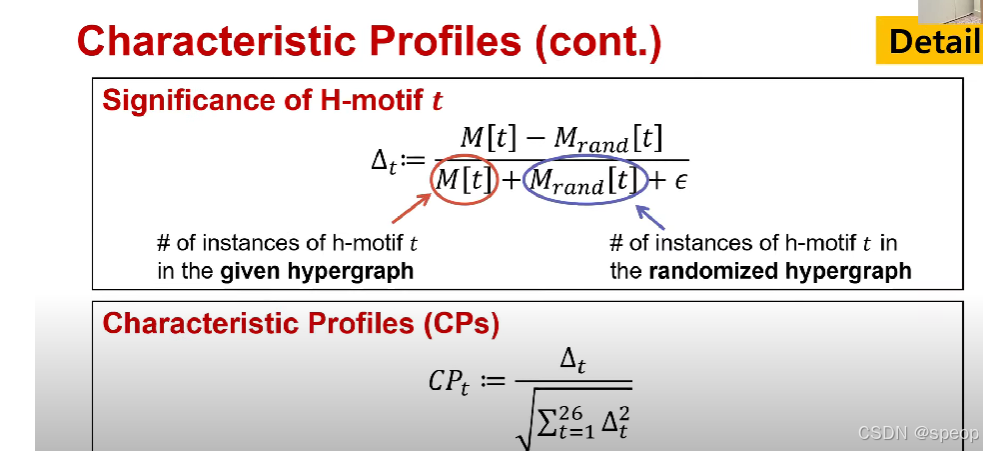
特征概貌（续）

• 超图模体$t$的重要性
  $${\Delta }_t:=\frac{M[t]-M_{\text{rand}}[t]}{M[t]+M_{\text{rand}}[t]+ϵ}$$
  其中，$M[t]$是给定超图中超图模体$t$的实例数量；$M_{\text{rand}}[t]$是随机化超图中超图模体$t$的实例数量。

我们有一个现实世界中的超图（比如描述蛋白质相互作用、社交网络关系等实际场景的超图），还有一个随机生成的超图（结构是随机的，用来做“基准对比”）。

对于某一个特定的超图模体$T$：

• 先统计 $T$ 在现实世界超图里出现的次数，记为 $M[t]$；
• 再统计 $T$ 在随机超图里出现的次数，记为 $M_{\text{rand}}[t]$。

然后用公式 ${\Delta }_t:=\frac{M[t]-M_{\text{rand}}[t]}{M[t]+M_{\text{rand}}[t]+ϵ}$ 来计算这个基序 $T$ 的“重要性”：

• 如果$M[t]>M_{\text{rand}}[t]$（现实中超图模体$T$ 出现得比随机情况多），那么分子$M[t]-M_{\text{rand}}[t]$ 是正数，整个${\Delta }_t$ 就会是正数，说明这个模体$T$ 在现实超图里是“更突出、更重要”的；
• 如果$M[t]<M_{\text{rand}}[t]$（现实中超图模体$T$ 出现得比随机情况少），分子是负数，整个${\Delta }_t$ 就会是负数，说明这个模体$T$在现实超图里是“不突出、甚至可能是被抑制”的。

简单说，就是通过和“随机情况”对比，看某个超图基序在现实场景里是“多出现”还是“少出现”，从而衡量它对现实超图结构的“重要程度”～

• 特征概貌（CPs）
  $$C{P}_t:=\frac{{\Delta }_t}{\sqrt{{\sum }_{t=1}^{26}{\Delta }_t^2}}$$
  我们构建了一个26维特征轮廓，如该等式所示，因此CP是一个紧凑的更好的向量，总结了给定超图的h模体信息
  由于我们对重要性进行了归一化，因此CPs中的值与超图的大小无关

真实超图与随机超图对比

• 真实世界的超图和随机超图在超图模体实例的分布上存在明显差异。

（图表说明：）

• 左侧图表为“coauth - DBLP”（合作作者 - DBLP数据集），右侧图表为“email - EU”（欧盟电子邮件数据集）；
• 图例中，绿色方块代表“真实世界超图”，红色圆圈代表“随机化超图”；
• 纵轴为“绝对数量（对数刻度）”，横轴为“超图模体索引”。

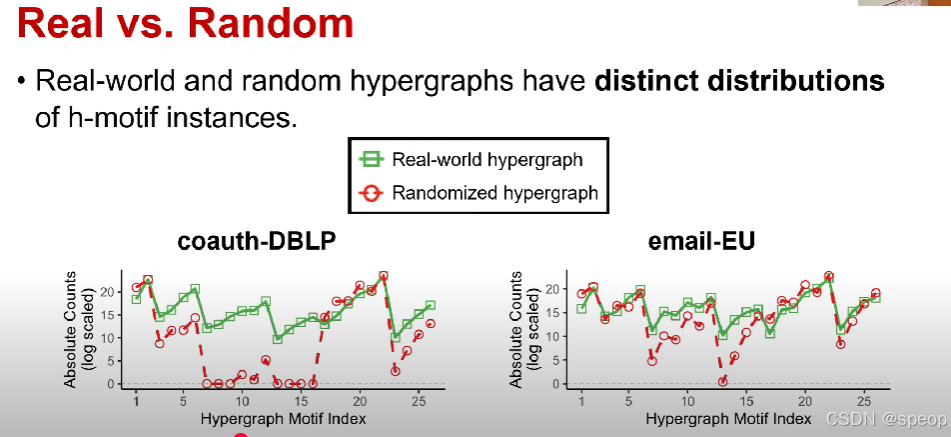
接下来我们绘制每个数据集的CPs，因此记录CPs是每个超图的26维向量
x轴是超图模体索引，从1到26，y轴是每个H模体的CPs
所以它基本上是相应H模体的归一化重要性
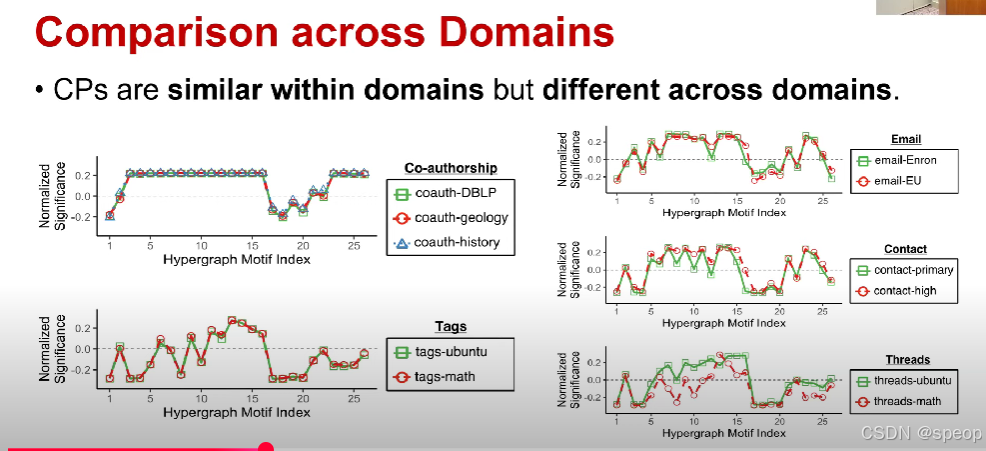
来自同一域的超图之间的 CPS 非常相似，但来自不同域的超图之间的 CPS 非常不同

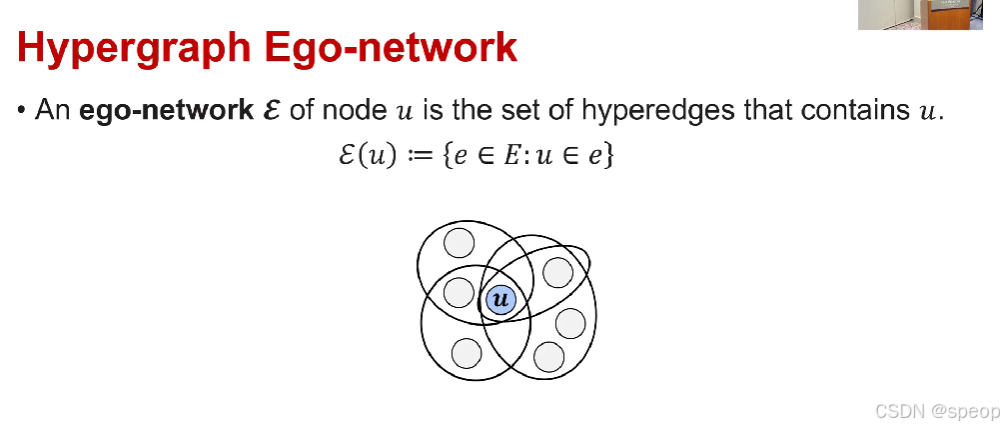
超图自我中心网络

• 节点 $u$ 的自我中心网络$\mathcal{E}$ 是包含$u$的超边的集合。
  E(u):={e∈E:u∈e}\mathcal{E}(u) := \{e \in E: u \in e\}E(u):={e∈E:u∈e}
  
  自我中心网络的密度
• 密度用于衡量超边的重叠紧密程度。
  $$\rho (\mathcal{E}):=\frac{|\mathcal{E}|}{\left|{\bigcup }_{e\in \mathcal{E}}e\right|}$$
  其中，$|\mathcal{E}|$表示子图中超边的数量，$\left|{\bigcup }_{e\in \mathcal{E}}e\right|$ 表示节点的数量。

（示例：）
自我中心网络$\mathcal{E}(u)$ 的密度为 $\frac{4}{7}$。

利用密度，我们可以测量与随机超图相比现实世界超图中超边重叠的程度
在这些图中，我们有三个不同超图的分布
x轴是自我网络中的节点数，y轴是自我网络的超边数
斜率表示超图自我网络的平均密度
斜率更陡峭，现实世界的超图与随机超图相比，现实世界的超图具有更高的密度

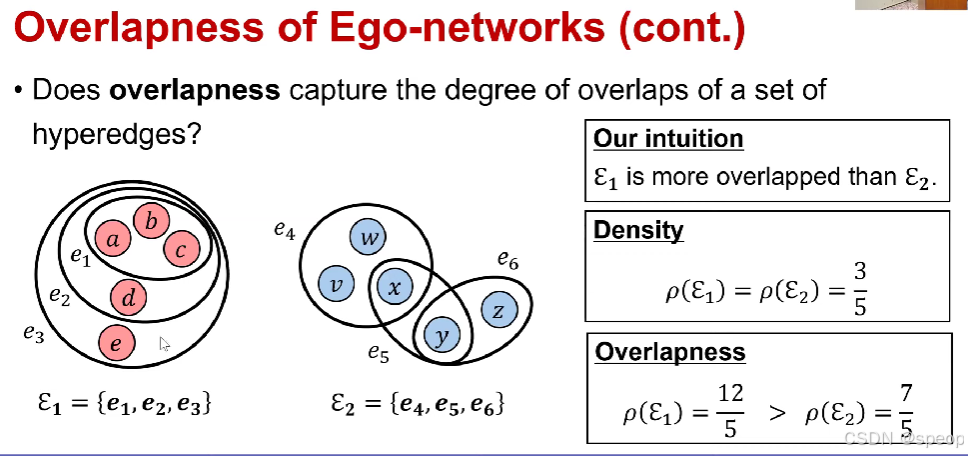
我们面临的一个问题是
密度能充分捕捉一组超边的重叠程度吗？
下图我们直觉是左边重叠更高，但是实际计算上重叠程度一样，与我们直觉相悖

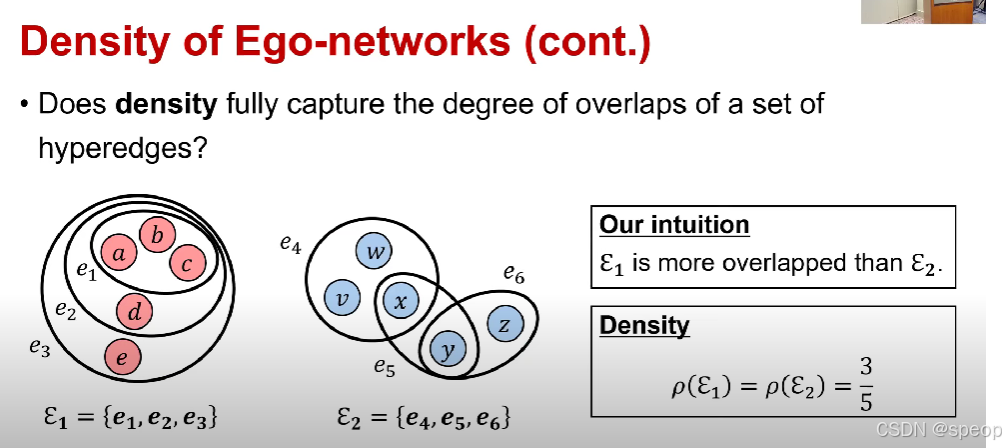
超边重叠程度

• 问题： 评估一组超边的重叠程度的合理度量是什么？
• 答案：
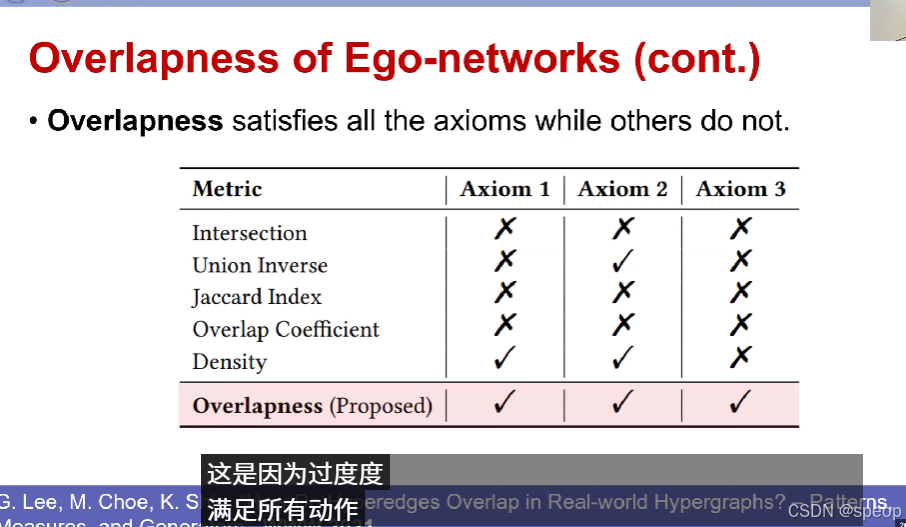
  • 我们提出了三条公理，任何合理的超边重叠度量都应满足这些公理。
  • 然后，我们提出了“重叠度（overlapness）”这一新的度量，它满足所有这些公理。

超边重叠程度（续）

• 公理1：超边数量
  考虑两组超边$\mathcal{E}$ 和${\mathcal{E}}^{\prime }$。
  如果$\mathcal{E}$ 和${\mathcal{E}}^{\prime }$ 满足（1）超边大小相同，且（2）不同节点的数量相同，但$\mathcal{E}$ 的超边数量比${\mathcal{E}}^{\prime }$ 多，那么$f(\mathcal{E})>f({\mathcal{E}}^{\prime })$。

超边重叠程度（续）

• 公理2：不同节点的数量
  考虑两组超边$\mathcal{E}$ 和${\mathcal{E}}^{\prime }$。
  如果$\mathcal{E}$ 和${\mathcal{E}}^{\prime }$ 满足（1）超边的数量相同，且（2）超边的大小分布相同，但$\mathcal{E}$ 的不同节点数量比${\mathcal{E}}^{\prime }$ 少，那么$f(\mathcal{E})>f({\mathcal{E}}^{\prime })$。

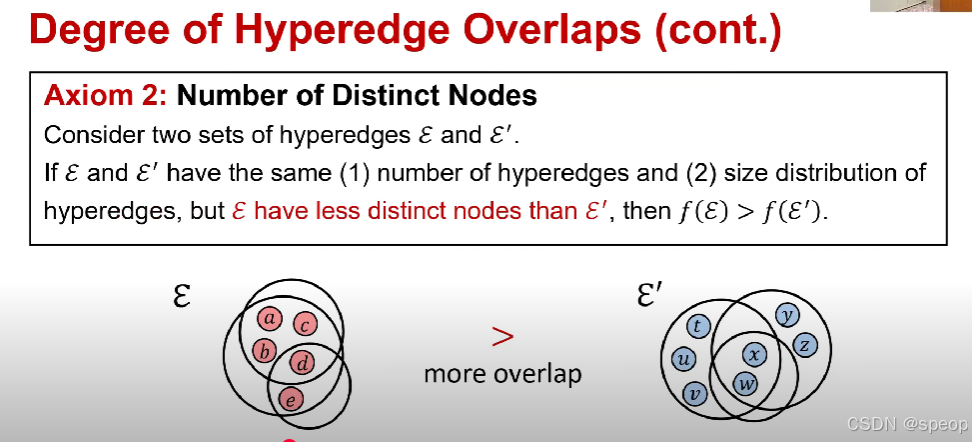
超边重叠程度（续）

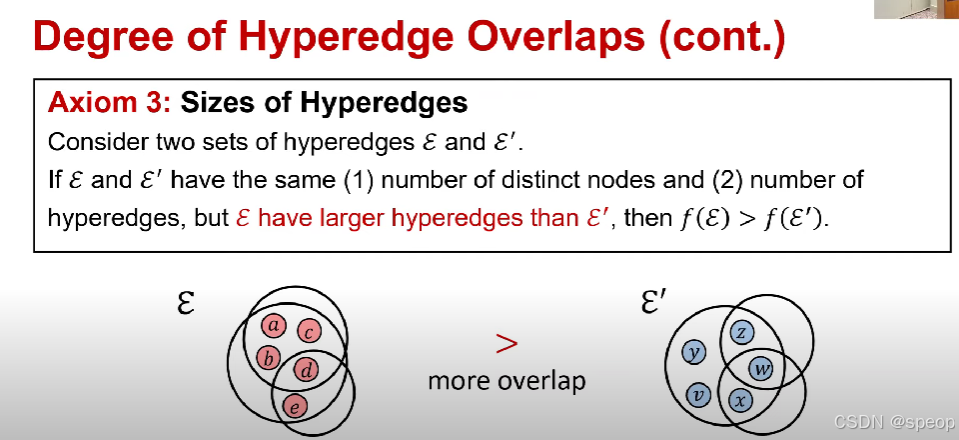
• 公理3：超边的大小
  考虑两组超边$\mathcal{E}$ 和${\mathcal{E}}^{\prime }$。
  如果$\mathcal{E}$和${\mathcal{E}}^{\prime }$ 满足（1）不同节点的数量相同，且（2）超边的数量相同，但$\mathcal{E}$ 的超边比${\mathcal{E}}^{\prime }$ 更大(更多的节点共享)，那么$f(\mathcal{E})>f({\mathcal{E}}^{\prime })$。
  

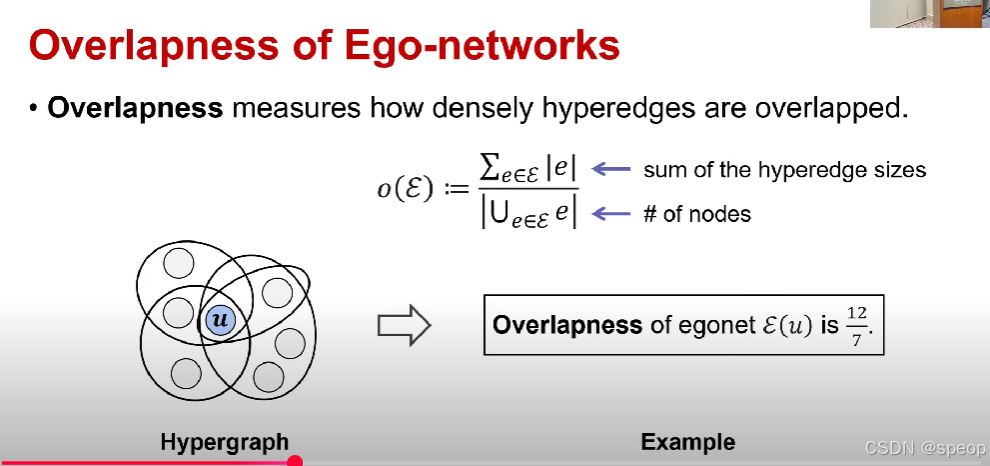
自我中心网络的重叠度

• 重叠度用于衡量超边的重叠紧密程度。

$$o(\mathcal{E}):=\frac{{\sum }_{e\in \mathcal{E}}|e|}{\left|{\bigcup }_{e\in \mathcal{E}}e\right|}$$
其中，${\sum }_{e\in \mathcal{E}}|e|$ 表示超边大小的总和，$\left|{\bigcup }_{e\in \mathcal{E}}e\right|$ 表示节点的数量。

（示例：）
自我中心网络$\mathcal{E}(u)$ 的重叠度为$\frac{12}{7}$。
使用上面的计算方法计算出来的

奇异值

奇异值是在矩阵的奇异值分解（Singular Value Decomposition，简称SVD）中产生的概念，是矩阵的一种重要特征值，在很多领域都有着关键意义，以下为你详细介绍：

定义与计算

对于任意一个 $m\times n$ 的实矩阵 $\mathbf{A}$，奇异值分解可以将矩阵 $\mathbf{A}$ 分解为三个矩阵的乘积，即 $\mathbf{A}=\mathbf{U}\Sigma {\mathbf{V}}^T$。

• $\mathbf{U}$ 是一个 $m\times m$ 的正交矩阵，它的列向量被称为左奇异向量；
• $\mathbf{V}$ 是一个 $n\times n$ 的正交矩阵，它的列向量被称为右奇异向量；
• $\Sigma$ 是一个 $m\times n$ 的对角矩阵，其主对角线上的元素 ${\sigma }_i$（$i=1,2,\cdots ,\min (m,n)$）就是矩阵 $\mathbf{A}$ 的奇异值，并且通常按照从大到小的顺序排列，即 ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_{\min (m,n)}\ge 0$。

计算奇异值，通常需要先计算矩阵 ${\mathbf{A}}^T\mathbf{A}$ 或 $\mathbf{A}{\mathbf{A}}^T$ 的特征值，再对这些特征值开平方得到奇异值（${\mathbf{A}}^T\mathbf{A}$ 与 $\mathbf{A}{\mathbf{A}}^T$ 的非零特征值相同，且这些非零特征值的平方根就是矩阵 $\mathbf{A}$ 的非零奇异值 ）。

几何意义

从线性变换的角度来看，矩阵可以看作是对向量进行线性变换的一种操作。对于矩阵 $\mathbf{A}$，它将 $n$ 维空间中的向量变换到 $m$ 维空间中。奇异值可以衡量这种变换在不同方向上的 “拉伸” 程度。

• 最大奇异值 ${\sigma }_1$ 表示矩阵 $\mathbf{A}$ 对向量进行变换时的最大拉伸倍数；
• 最小奇异值 ${\sigma }_{\min (m,n)}$ 表示最小拉伸倍数；
• 其他奇异值介于两者之间，反映了矩阵在不同方向上的变换能力。

与矩阵性质的关系

• 矩阵的秩：矩阵 $\mathbf{A}$ 的秩等于其非零奇异值的个数。通过奇异值分解，可以很方便地确定矩阵的秩，例如如果一个矩阵经过奇异值分解后，只有前 $r$ 个奇异值非零，那么该矩阵的秩就是 $r$ 。
• 矩阵的条件数：矩阵 $\mathbf{A}$ 的条件数 $\text{cond}(\mathbf{A})$ 定义为最大奇异值与最小奇异值的比值，即 $\text{cond}(\mathbf{A})=\frac{{\sigma }_1}{{\sigma }_{\min (m,n)}}$。条件数反映了矩阵的 “病态” 程度，条件数越大，矩阵越接近奇异矩阵（不可逆矩阵），在数值计算中就越容易出现不稳定的情况。

实际应用场景

• 图像处理：用于图像压缩，保留较大奇异值对应的部分，去除较小奇异值对应的信息，在几乎不影响视觉效果的前提下，大幅减小图像存储所需空间。
• 机器学习：在主成分分析（PCA）中，通过奇异值分解来提取数据的主成分，实现数据降维，提高模型训练效率；也可用于推荐系统，通过对用户 - 物品评分矩阵进行奇异值分解来预测用户偏好，提供个性化推荐 。
• 信号处理：可以实现信号降噪，去除噪声对应的较小奇异值成分，恢复纯净信号；还能用于信号特征提取，根据奇异值分布判断信号类型或状态。

交叉熵

交叉熵（Cross Entropy）是信息论中的一个重要概念，在机器学习、深度学习等领域有着广泛应用，用于衡量两个概率分布之间的差异。以下从多个方面详细介绍交叉熵：

信息论中的定义

在信息论里，信息熵（Entropy）用于描述一个随机变量的不确定性。对于一个离散随机变量 $X$，其取值为 $x_i$$(i=1,2,\cdots ,n$ ），概率分布为 $p(x_i)$，信息熵 $H(p)$ 的计算公式为：
$H(p)=-{\sum }_{i=1}^{n}p(x_i)\log p(x_i)$
它表示对随机变量进行编码所需的平均比特数，熵值越大，随机变量的不确定性越高。

而交叉熵是用来衡量用概率分布 $q$ 来近似概率分布 $p$ 时所损失的信息量。对于离散随机变量 $X$，概率分布 $p$ 和 $q$ 的交叉熵 $H(p,q)$ 定义为：
$H(p,q)=-{\sum }_{i=1}^{n}p(x_i)\log q(x_i)$
其中，$p(x_i)$ 是真实分布，$q(x_i)$ 是预测分布 。

机器学习中的应用

在机器学习，特别是分类任务中，交叉熵常被用作损失函数，以评估模型预测结果与真实标签之间的差异。

• 二分类问题：假设真实标签 $y$ 取值为 $0$ 或$1$，预测为正类的概率是 $\hat{y}$，则交叉熵损失函数 $L$ 可以表示为：
  $L=-[y\log \hat{y}+(1-y)\log (1-\hat{y})]$
  当真实标签 $y=1$ 时，损失函数只与 $\log \hat{y}$ 有关，$\hat{y}$ 越接近 $1$（即预测越准确），损失值越小；当 $y=0$ 时，损失函数与 $\log (1-\hat{y})$ 有关，$\hat{y}$ 越接近 $0$，损失值越小。

• 多分类问题：常见的是使用Softmax函数将模型的输出转化为概率分布，然后用交叉熵计算损失。假设有 $C$ 个类别，样本 $x$ 的真实标签为 $y$（是一个one - hot编码向量，只有对应类别位置为 $1$，其余为 $0$ ），模型预测样本 $x$ 属于第 $i$ 类的概率为 $p_i$，则交叉熵损失函数为：
  $L=-{\sum }_{i=1}^C{y}_i\log p_i$
  因为 $y$是one - hot编码，只有一个位置为 $1$，所以实际上就是对真实类别对应的预测概率取对数再取负，预测概率越接近 $1$ ，损失越小。

交叉熵作为损失函数的优势

• 梯度特性好：相比于均方误差（MSE）损失函数，在分类问题中，交叉熵作为损失函数时，模型训练过程中梯度更新更合理，能让模型更快收敛。例如在使用Sigmoid函数作为激活函数的神经网络中，MSE损失函数可能会导致梯度消失问题，而交叉熵损失函数可以避免这一问题。
• 符合直观理解：交叉熵直接衡量了预测分布与真实分布的差异，预测结果越接近真实标签，交叉熵值越低，能很好地反映模型在分类任务上的性能表现。

与相对熵（KL散度）的关系

相对熵，即KL散度（Kullback - Leibler Divergence），用于衡量两个概率分布 $p$ 和 $q$ 之间的差异，定义为：
$D_{KL}(p||q)={\sum }_{i=1}^{n}p(x_i)\log \frac{p(x_i)}{q(x_i)}=H(p,q)-H(p)$
可以看出，交叉熵等于信息熵加上KL散度。在机器学习中，当真实分布 $p$ 固定时，信息熵 $H(p)$ 是一个常数，此时最小化交叉熵 $H(p,q)$ 就等价于最小化KL散度$D_{KL}(p||q)$，也就是让预测分布$q$尽可能接近真实分布$p$ 。

局部聚类系数

要理解局部聚类系数和图的聚类系数，我们可以分步拆解：

一、局部聚类系数（以节点 ( u ) 为例）

局部聚类系数衡量一个节点的“邻居之间互相连接的紧密程度”。

计算逻辑：

假设节点 ( u ) 有 ( k ) 个邻居（即与 ( u ) 直接相连的节点数）。

• 邻居之间“最多能形成的边数”：如果 ( k ) 个邻居之间两两都相连，边数为 ( \binom{k}{2} = \frac{k(k - 1)}{2} )（组合数，从 ( k ) 个邻居中选 2 个连边的总可能数）。
• 实际观察到的邻居之间的边数：记为 ( E )（即“邻居的朋友”之间真的有连接的对数）。

那么，节点 ( u ) 的局部聚类系数 ( C_u ) 定义为：
[ C_u = \frac{\text{实际邻居间的边数 } E}{\text{邻居间最多能有的边数 } \binom{k}{2}} ]

结合例子理解（节点 ( u ) 有 5 个邻居）：

• 邻居数 ( k = 5 )，则邻居间最多能有的边数为 ( \binom{5}{2} = \frac{5 \times 4}{2} = 10 )（即“最多可以有 10 对连接”）。
• 实际观察到邻居间有 3 对连接（即 ( E = 3 )）。

因此，节点 ( u ) 的局部聚类系数：
[ C_u = \frac{3}{10} ]

二、图的聚类系数

图的聚类系数是整个图中所有节点的“局部聚类系数”的平均值，用于衡量“整个图的聚类程度（即图中节点的邻居们互相连接的整体紧密性）”。

假设图的节点集合为 ( V )，( |V| ) 是节点总数，每个节点 ( v \in V ) 都有自己的局部聚类系数 ( C_v )。

则图的聚类系数 ( C ) 定义为：
[ C = \frac{1}{|V|} \sum_{v \in V} C_v ]

简单来说：先算出每个节点的局部聚类系数，再把所有节点的局部聚类系数加起来，最后除以节点总数，得到的就是“整个图的平均聚类紧密程度”。

总结

• 局部聚类系数：聚焦单个节点的邻居之间的连接紧密性，公式是“实际邻居连边数 ÷ 邻居最大可能连边数”。
• 图的聚类系数：聚焦整个图的平均聚类紧密性，公式是“所有节点的局部聚类系数的平均值”。

例子中节点 ( u ) 的局部聚类 ( \frac{3}{10} )，就是“实际 3 对邻居连边”除以“最多 10 对邻居连边”；而图的聚类系数，就是把所有节点的这类局部值平均一下～