《算法导论》第 19 章 - 斐波那契堆
引言
斐波那契堆(Fibonacci Heap)是一种高效的可合并堆数据结构,由 Michael L. Fredman 和 Robert E. Tarjan 于 1984 年提出。它在许多优先队列操作中提供了极佳的 amortized(摊还)时间复杂度,尤其适用于需要频繁进行合并操作的场景。
19.1 斐波那契堆结构
19.1.1 基本结构
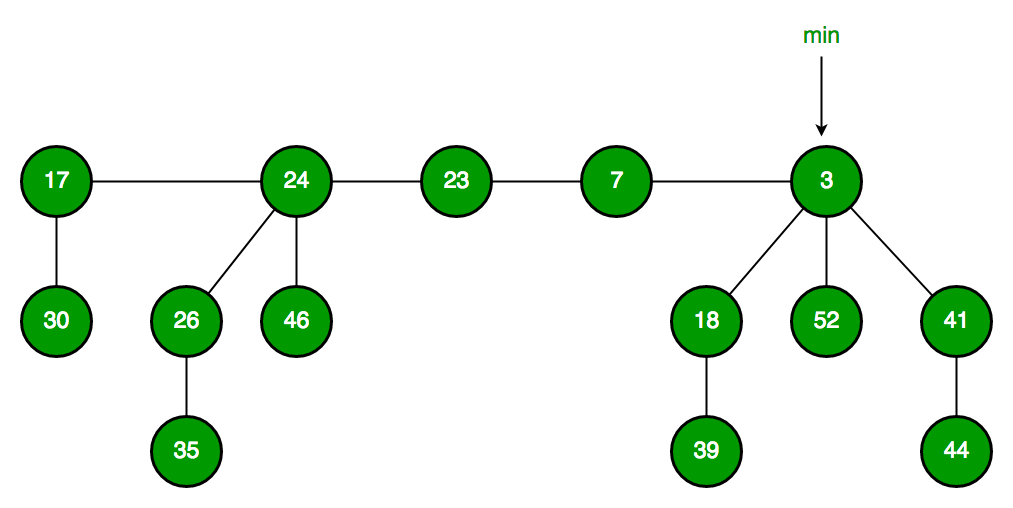
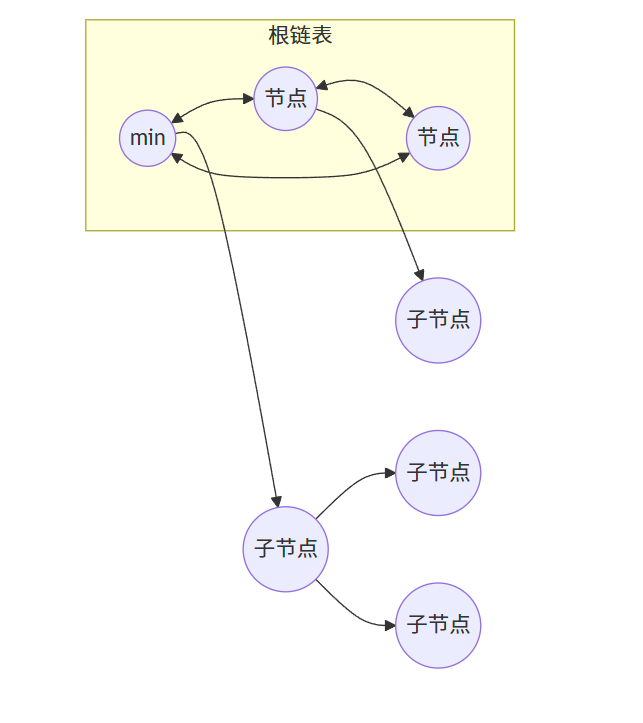
斐波那契堆由一组满足最小堆性质的树组成,这些树都是无序的多叉树。它包含以下关键组件:
- 一个指向具有最小关键字的节点的指针(min pointer)
- 所有树的根节点通过双向循环链表连接
- 每个节点包含:
- 关键字值
- 父节点指针
- 子节点指针
- 左、右兄弟节点指针
- 度数(子节点数量)
- 一个标记(用于删除操作)
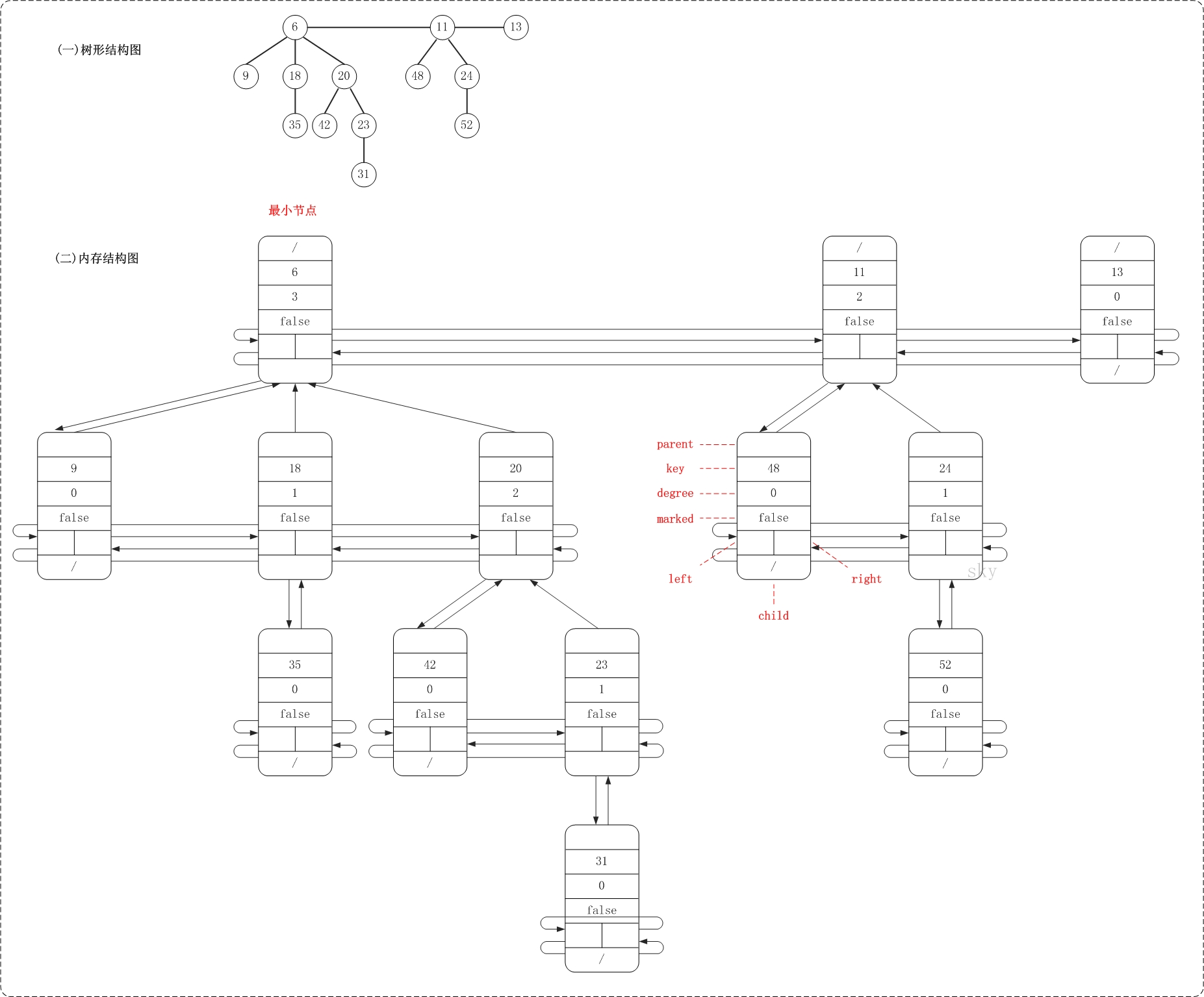
19.1.2 节点结构定义
下面是斐波那契堆节点的 C++ 结构定义:
#ifndef FIBONACCI_HEAP_H
#define FIBONACCI_HEAP_H#include <iostream>
#include <vector>
#include <stdexcept>// 斐波那契堆节点结构
template <typename T>
struct FibonacciNode {T key; // 节点存储的值int degree; // 节点的度数(子节点数量)bool mark; // 标记,用于删除操作FibonacciNode* parent; // 父节点指针FibonacciNode* child; // 子节点指针FibonacciNode* left; // 左兄弟节点指针FibonacciNode* right; // 右兄弟节点指针// 构造函数FibonacciNode(const T& k) : key(k), degree(0), mark(false),parent(nullptr), child(nullptr),left(this), right(this) {}
};// 斐波那契堆类
template <typename T>
class FibonacciHeap {
private:FibonacciNode<T>* minNode; // 指向最小节点的指针int nodeCount; // 堆中节点的总数// 将节点y从其所在的双向链表中移除void removeNode(FibonacciNode<T>* y);// 将节点y插入到以节点x为头的双向链表中void addNode(FibonacciNode<T>* x, FibonacciNode<T>* y);// 将节点y设为节点x的子节点void link(FibonacciNode<T>* y, FibonacciNode<T>* x);// 合并相同度数的树void consolidate();// 切断节点y与其父节点x之间的连接void cut(FibonacciNode<T>* y, FibonacciNode<T>* x);// 级联切断操作void cascadingCut(FibonacciNode<T>* y);// 销毁堆的辅助函数void destroyHeap(FibonacciNode<T>* node);public:// 构造函数FibonacciHeap() : minNode(nullptr), nodeCount(0) {}// 析构函数~FibonacciHeap();// 插入元素FibonacciNode<T>* insert(const T& key);// 查找最小元素const T& findMin() const;// 抽取最小元素T extractMin();// 合并两个斐波那契堆void merge(FibonacciHeap<T>& other);// 减小关键字值void decreaseKey(FibonacciNode<T>* x, const T& k);// 删除节点void deleteNode(FibonacciNode<T>* x);// 检查堆是否为空bool isEmpty() const { return nodeCount == 0; }// 获取堆中节点数量int size() const { return nodeCount; }
};#endif // FIBONACCI_HEAP_H
19.2 可合并堆操作
斐波那契堆支持可合并堆的所有操作,并且大部分操作都能在常数摊还时间内完成。
19.2.1 插入操作
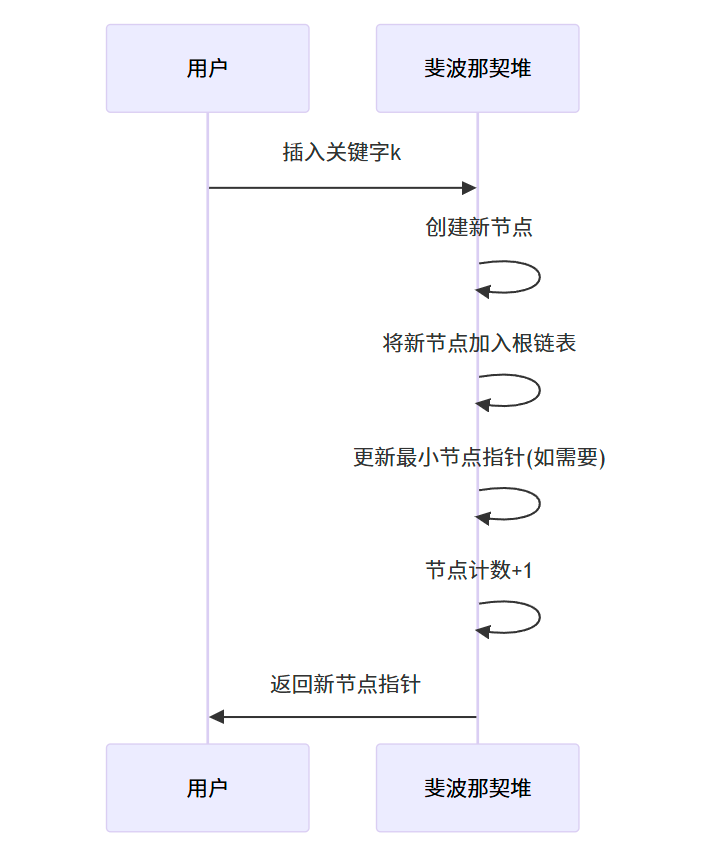
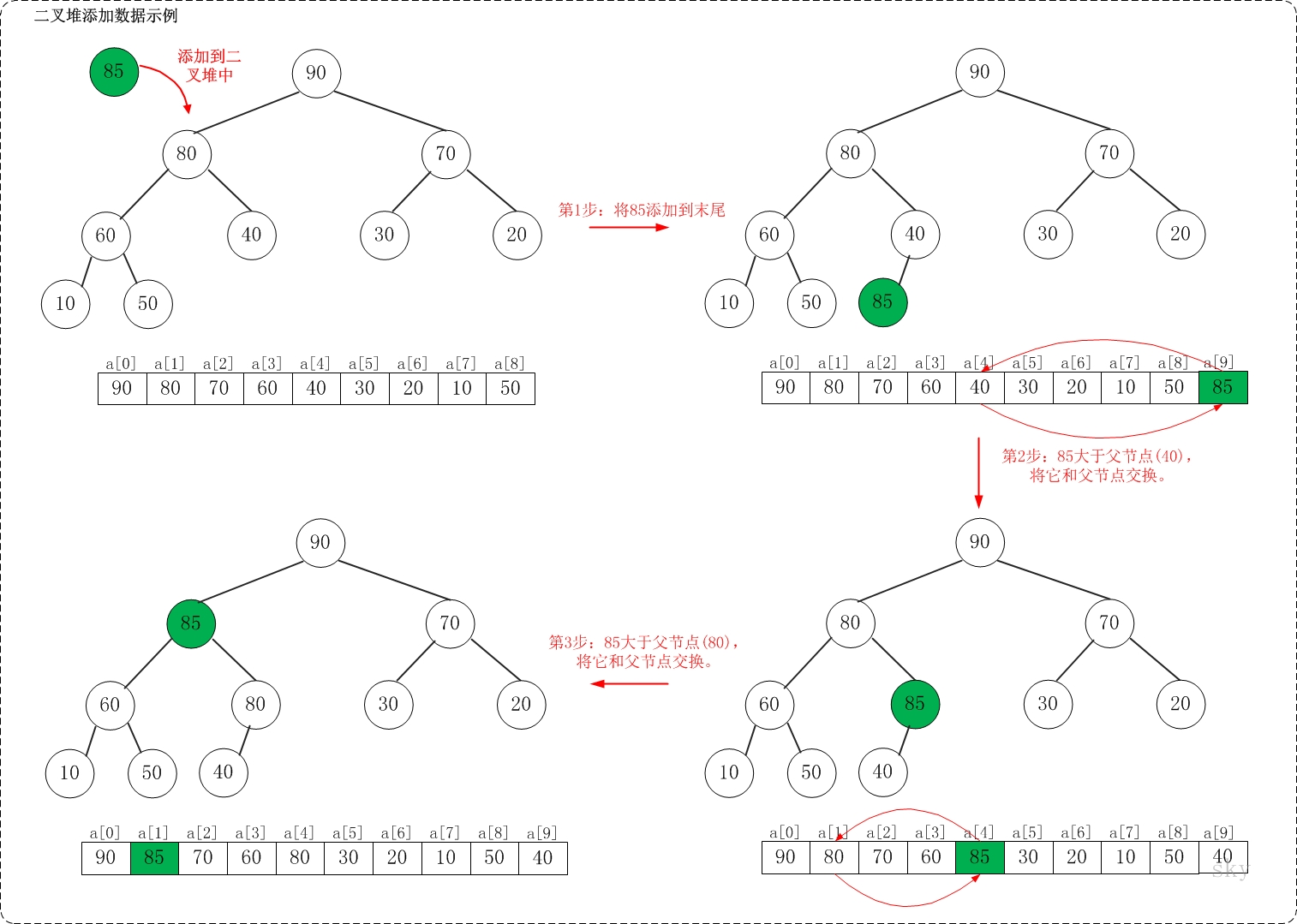
插入操作非常简单,只需创建一个新节点,将其添加到根链表中,并更新最小节点指针(如果需要)。
步骤:
- 创建一个包含关键字的新节点
- 将新节点加入根链表
- 如果新节点的关键字小于当前最小节点的关键字,更新最小节点指针
- 节点计数加 1
19.2.2 查找最小元素
由于斐波那契堆维护了一个指向最小元素的指针,因此查找最小元素可以在 O (1) 时间内完成。
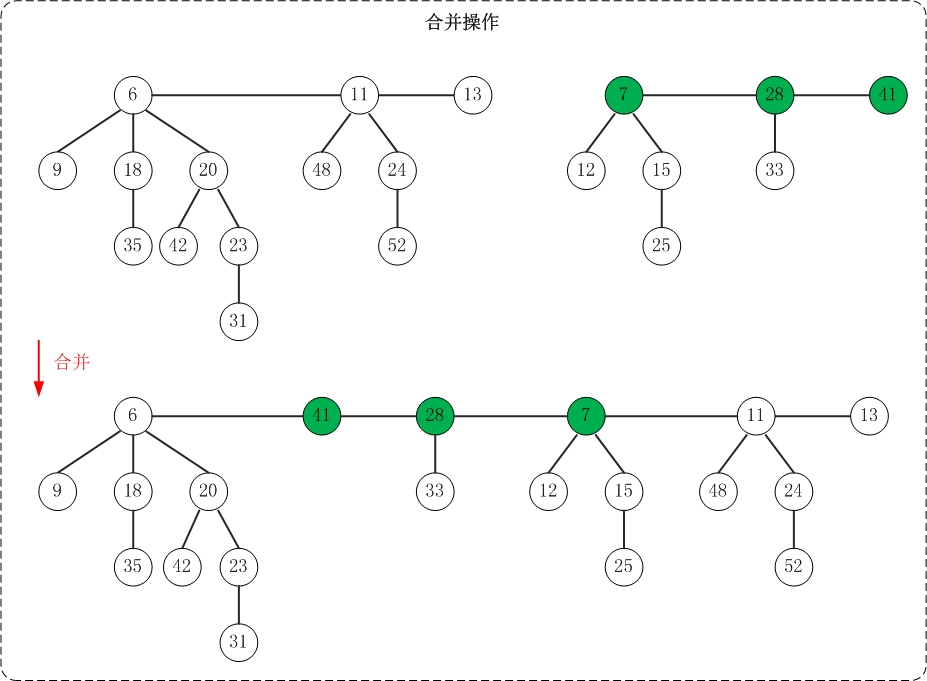
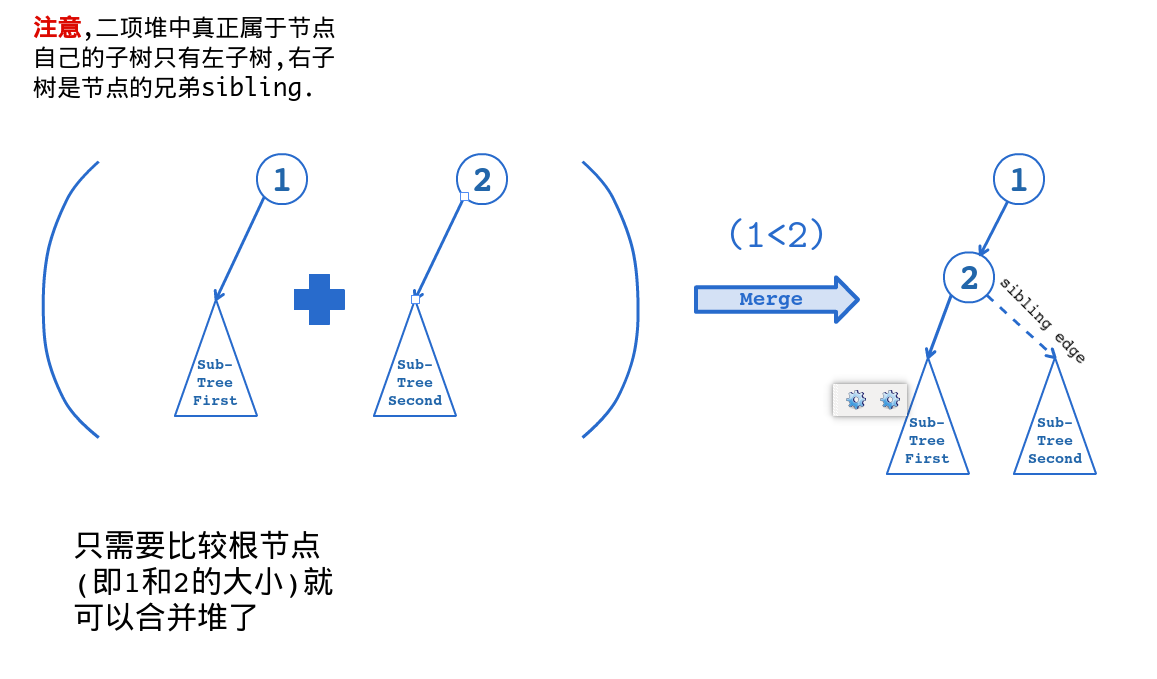
19.2.3 合并操作
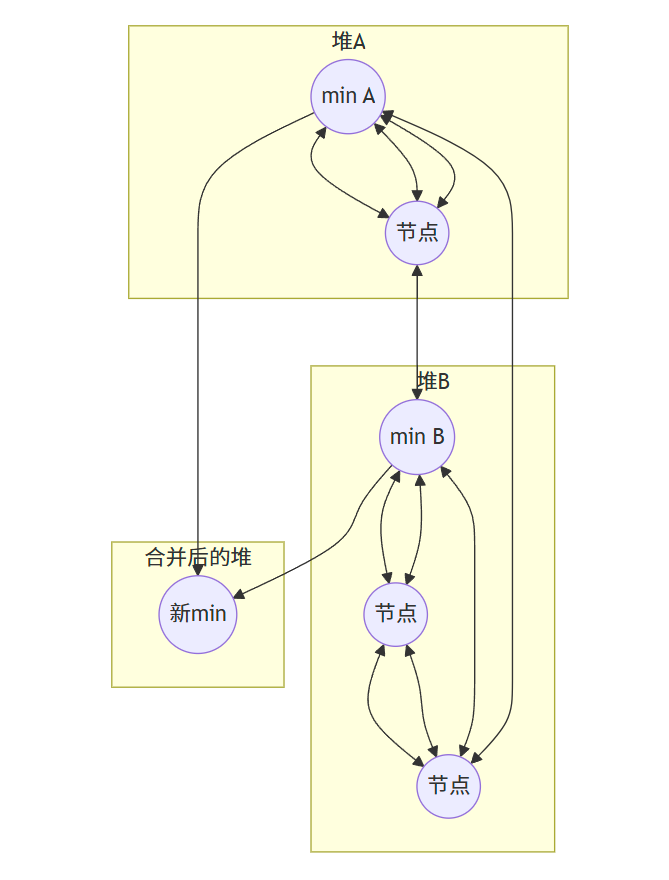
合并两个斐波那契堆只需将它们的根链表合并成一个双向链表,并更新最小节点指针。
步骤:
- 合并两个堆的根链表
- 更新最小节点指针,指向两个堆中较小的那个最小节点
- 更新节点计数
19.2.4 抽取最小元素
抽取最小元素是斐波那契堆中最复杂的操作之一,需要进行 "合并"(consolidate)过程来维持斐波那契堆的性质。
步骤:
- 记录最小节点的值
- 将最小节点的所有子节点添加到根链表
- 从根链表中移除最小节点
- 执行 consolidate 操作,合并度数相同的树
- 更新最小节点指针
- 节点计数减 1
- 返回记录的最小节点值
下面是上述操作的 C++ 实现:
#include "fibonacci_heap.h"// 将节点y从其所在的双向链表中移除
template <typename T>
void FibonacciHeap<T>::removeNode(FibonacciNode<T>* y) {y->left->right = y->right;y->right->left = y->left;
}// 将节点y插入到以节点x为头的双向链表中
template <typename T>
void FibonacciHeap<T>::addNode(FibonacciNode<T>* x, FibonacciNode<T>* y) {y->left = x->left;y->right = x;x->left->right = y;x->left = y;
}// 将节点y设为节点x的子节点
template <typename T>
void FibonacciHeap<T>::link(FibonacciNode<T>* y, FibonacciNode<T>* x) {// 从根链表中移除yremoveNode(y);y->parent = x;// 将y添加为x的子节点if (x->child == nullptr) {x->child = y;y->left = y->right = y;} else {addNode(x->child, y);}x->degree++; // 增加x的度数y->mark = false; // 重置y的标记
}// 合并相同度数的树
template <typename T>
void FibonacciHeap<T>::consolidate() {// 计算最大可能度数int maxDegree = 0;FibonacciNode<T>* current = minNode;if (current != nullptr) {do {if (current->degree > maxDegree) {maxDegree = current->degree;}current = current->right;} while (current != minNode);}// 创建度数表std::vector<FibonacciNode<T>*> degreeTable(maxDegree + 1, nullptr);// 遍历根链表中的所有节点while (minNode != nullptr) {FibonacciNode<T>* x = minNode;int d = x->degree;// 移除当前节点,以便后续处理removeNode(x);x->left = x->right = x; // 暂时形成一个单节点链表// 合并度数相同的树while (degreeTable[d] != nullptr) {FibonacciNode<T>* y = degreeTable[d];// 确保x是关键字较小的节点if (x->key > y->key) {std::swap(x, y);}// 将y链接到xlink(y, x);degreeTable[d] = nullptr;d++;}degreeTable[d] = x;}// 重置最小节点指针minNode = nullptr;// 重建根链表并找到新的最小节点for (int i = 0; i <= maxDegree; i++) {if (degreeTable[i] != nullptr) {if (minNode == nullptr) {minNode = degreeTable[i];minNode->left = minNode->right = minNode;} else {addNode(minNode, degreeTable[i]);if (degreeTable[i]->key < minNode->key) {minNode = degreeTable[i];}}}}
}// 插入元素
template <typename T>
FibonacciNode<T>* FibonacciHeap<T>::insert(const T& key) {FibonacciNode<T>* newNode = new FibonacciNode<T>(key);if (minNode == nullptr) {// 堆为空,新节点成为根节点minNode = newNode;} else {// 将新节点添加到根链表addNode(minNode, newNode);// 更新最小节点if (newNode->key < minNode->key) {minNode = newNode;}}nodeCount++;return newNode;
}// 查找最小元素
template <typename T>
const T& FibonacciHeap<T>::findMin() const {if (minNode == nullptr) {throw std::runtime_error("Heap is empty");}return minNode->key;
}// 抽取最小元素
template <typename T>
T FibonacciHeap<T>::extractMin() {if (minNode == nullptr) {throw std::runtime_error("Heap is empty");}FibonacciNode<T>* z = minNode;T minKey = z->key;// 将z的所有子节点添加到根链表if (z->child != nullptr) {FibonacciNode<T>* child = z->child;do {FibonacciNode<T>* nextChild = child->right;// 移除子节点的父指针child->parent = nullptr;// 将子节点添加到根链表addNode(minNode, child);child = nextChild;} while (child != z->child);}// 从根链表中移除zremoveNode(z);// 如果z是堆中唯一的节点if (z == z->right) {minNode = nullptr;} else {minNode = z->right;// 合并相同度数的树consolidate();}nodeCount--;delete z;return minKey;
}// 合并两个斐波那契堆
template <typename T>
void FibonacciHeap<T>::merge(FibonacciHeap<T>& other) {if (other.minNode == nullptr) {return; // 另一个堆为空,无需合并}if (minNode == nullptr) {// 当前堆为空,直接使用另一个堆minNode = other.minNode;nodeCount = other.nodeCount;} else {// 合并两个根链表FibonacciNode<T>* thisLeft = minNode->left;FibonacciNode<T>* otherLeft = other.minNode->left;minNode->left = otherLeft;otherLeft->right = minNode;thisLeft->right = other.minNode;other.minNode->left = thisLeft;// 更新最小节点if (other.minNode->key < minNode->key) {minNode = other.minNode;}nodeCount += other.nodeCount;}// 清空另一个堆other.minNode = nullptr;other.nodeCount = 0;
}// 析构函数
template <typename T>
FibonacciHeap<T>::~FibonacciHeap() {if (minNode != nullptr) {destroyHeap(minNode);}
}// 销毁堆的辅助函数
template <typename T>
void FibonacciHeap<T>::destroyHeap(FibonacciNode<T>* node) {if (node == nullptr) return;FibonacciNode<T>* current = node;bool isFirst = true;// 遍历当前链表中的所有节点while (isFirst || current != node) {isFirst = false;FibonacciNode<T>* next = current->right;// 递归销毁子节点destroyHeap(current->child);delete current;current = next;}
}
19.2.5 综合案例:优先级队列
斐波那契堆非常适合实现优先级队列,特别是需要频繁合并操作的场景。以下是一个使用斐波那契堆实现优先级队列的示例:
#include "fibonacci_heap.h"
#include <iostream>
#include <string>// 任务结构体,表示一个优先级队列中的任务
struct Task {int priority; // 优先级,值越小优先级越高std::string description; // 任务描述// 重载小于运算符,用于斐波那契堆的比较bool operator<(const Task& other) const {return priority < other.priority;}// 重载大于运算符bool operator>(const Task& other) const {return priority > other.priority;}
};// 输出任务信息
std::ostream& operator<<(std::ostream& os, const Task& task) {os << "任务: " << task.description << ", 优先级: " << task.priority;return os;
}int main() {try {// 创建两个斐波那契堆作为优先级队列FibonacciHeap<Task> pq1, pq2;// 向第一个优先级队列添加任务pq1.insert({3, "完成算法作业"});pq1.insert({1, "紧急会议"});pq1.insert({5, "回复邮件"});// 向第二个优先级队列添加任务pq2.insert({2, "准备演示文稿"});pq2.insert({4, "整理文档"});std::cout << "合并前的优先级队列1大小: " << pq1.size() << std::endl;std::cout << "合并前的优先级队列2大小: " << pq2.size() << std::endl;// 合并两个优先级队列pq1.merge(pq2);std::cout << "合并后的优先级队列大小: " << pq1.size() << std::endl;std::cout << "合并后队列为空? " << (pq1.isEmpty() ? "是" : "否") << std::endl;std::cout << "被合并的队列为空? " << (pq2.isEmpty() ? "是" : "否") << std::endl;// 按优先级处理任务std::cout << "\n按优先级处理任务:" << std::endl;while (!pq1.isEmpty()) {Task highestPriority = pq1.extractMin();std::cout << "处理: " << highestPriority << std::endl;}std::cout << "\n所有任务处理完毕,队列为空? " << (pq1.isEmpty() ? "是" : "否") << std::endl;} catch (const std::exception& e) {std::cerr << "发生错误: " << e.what() << std::endl;return 1;}return 0;
}
19.3 关键字减值和删除一个结点
19.3.1 关键字减值
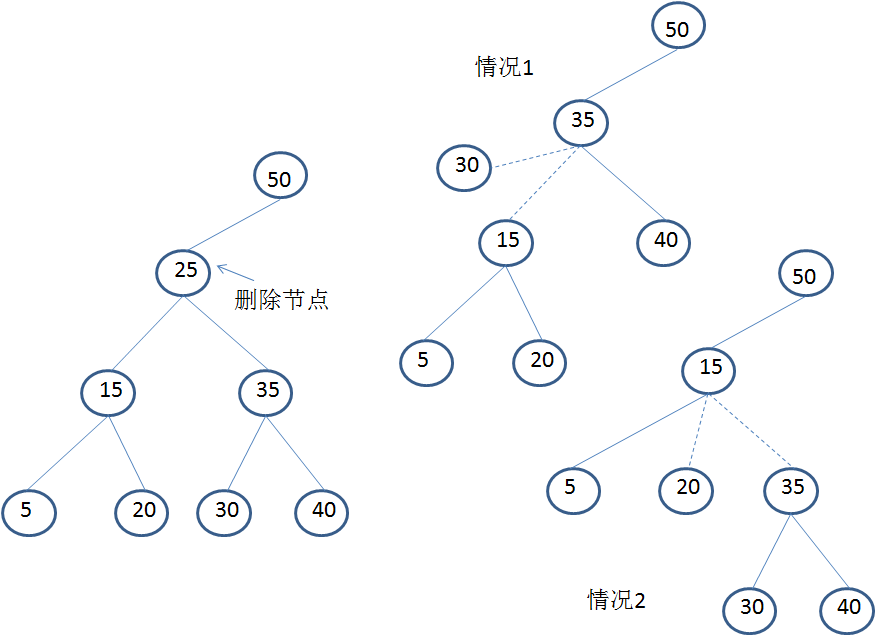
关键字减值操作用于减小某个节点的关键字值,并可能需要调整堆的结构以维持最小堆性质。
步骤:
- 如果新关键字大于当前关键字,抛出异常
- 更新节点的关键字值
- 如果节点的父节点关键字大于新关键字,切断该节点与父节点的连接
- 执行级联切断操作,确保斐波那契堆的性质
19.3.2 切断和级联切断
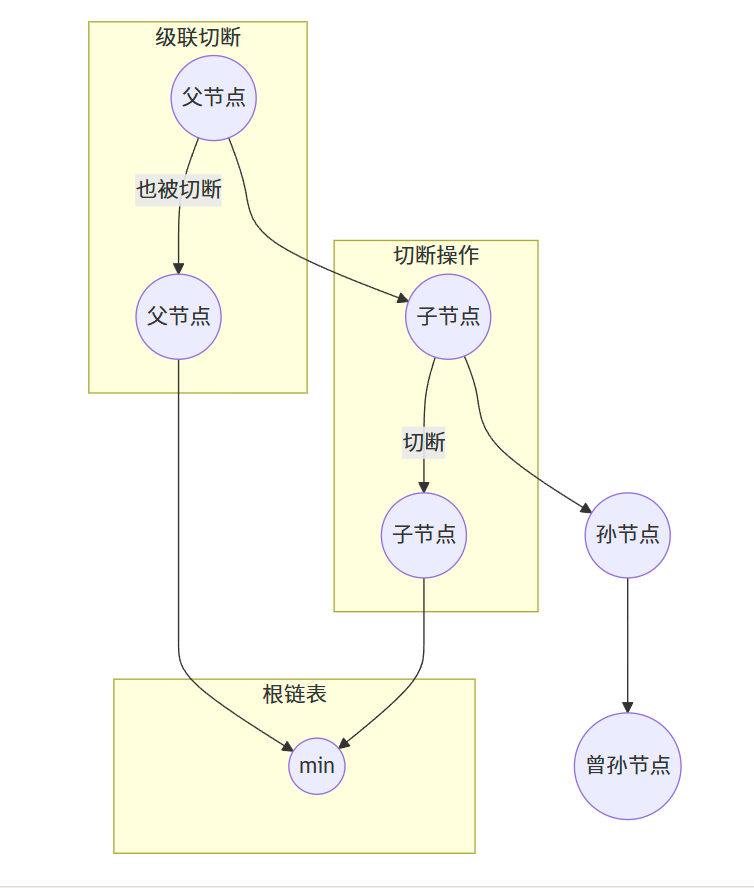
- 切断(cut):将一个节点从其父节点的子链表中移除,并将其添加到根链表中
- 级联切断(cascading cut):如果一个节点的子节点被切断,检查该节点是否也需要被切断,递归执行直到遇到一个未被标记的节点或根节点
19.3.3 删除一个节点
删除一个节点可以通过以下步骤实现:
- 将该节点的关键字减值为负无穷大(或最小可能值)
- 执行抽取最小元素操作,将该节点从堆中移除
下面是关键字减值和删除操作的 C++ 实现:
#include "fibonacci_heap.h"// 切断节点y与其父节点x之间的连接
template <typename T>
void FibonacciHeap<T>::cut(FibonacciNode<T>* y, FibonacciNode<T>* x) {// 从x的子链表中移除yremoveNode(y);x->degree--;// 如果x的子节点指针指向y,更新子节点指针if (x->child == y) {x->child = y->right;if (x->child == y) { // 如果y是x唯一的子节点x->child = nullptr;}}// 将y添加到根链表addNode(minNode, y);y->parent = nullptr;y->mark = false; // 重置标记
}// 级联切断操作
template <typename T>
void FibonacciHeap<T>::cascadingCut(FibonacciNode<T>* y) {FibonacciNode<T>* z = y->parent;if (z != nullptr) {if (!y->mark) {// 如果y未被标记,标记它y->mark = true;} else {// 如果y已被标记,切断y并继续级联切断cut(y, z);cascadingCut(z);}}
}// 减小关键字值
template <typename T>
void FibonacciHeap<T>::decreaseKey(FibonacciNode<T>* x, const T& k) {if (k > x->key) {throw std::invalid_argument("New key is larger than current key");}x->key = k;FibonacciNode<T>* y = x->parent;// 如果x的关键字小于其父节点的关键字,需要调整if (y != nullptr && x->key < y->key) {cut(x, y);cascadingCut(y);}// 更新最小节点if (x->key < minNode->key) {minNode = x;}
}// 删除节点
template <typename T>
void FibonacciHeap<T>::deleteNode(FibonacciNode<T>* x) {// 将x的关键字减小到负无穷大(这里使用一个非常小的值模拟)T minPossible = x->key;// 假设T是数值类型,这里简单地将其设置为一个极小值decreaseKey(x, minPossible - minPossible - minPossible);// 抽取最小元素(即x)extractMin();
}// 显式实例化常用类型,避免链接错误
template class FibonacciHeap<int>;
template class FibonacciHeap<double>;
template class FibonacciHeap<Task>; // 为前面示例中的Task类型实例化
19.3.4 综合案例:动态优先级调整
在许多实际应用中,我们需要能够动态调整任务的优先级。以下示例展示了如何使用斐波那契堆的关键字减值操作来实现这一功能:
#include "fibonacci_heap.h"
#include <iostream>
#include <string>
#include <vector>// 任务结构体
struct Task {int priority;std::string description;bool operator<(const Task& other) const {return priority < other.priority;}bool operator>(const Task& other) const {return priority > other.priority;}
};// 输出任务信息
std::ostream& operator<<(std::ostream& os, const Task& task) {os << "[" << task.priority << "] " << task.description;return os;
}int main() {try {FibonacciHeap<Task> taskHeap;std::vector<FibonacciNode<Task>*> taskNodes;// 添加一些初始任务taskNodes.push_back(taskHeap.insert({5, "编写文档"}));taskNodes.push_back(taskHeap.insert({3, "测试代码"}));taskNodes.push_back(taskHeap.insert({7, "修复低优先级bug"}));taskNodes.push_back(taskHeap.insert({2, "准备会议"}));taskNodes.push_back(taskHeap.insert({8, "优化性能"}));std::cout << "初始任务队列:" << std::endl;FibonacciHeap<Task> tempHeap;tempHeap.merge(taskHeap); // 创建一个副本用于展示while (!tempHeap.isEmpty()) {std::cout << " " << tempHeap.extractMin() << std::endl;}// 调整一些任务的优先级std::cout << "\n调整任务优先级:" << std::endl;std::cout << " 将\"修复低优先级bug\"的优先级从7调整为1" << std::endl;taskHeap.decreaseKey(taskNodes[2], {1, "修复紧急bug"});std::cout << " 将\"优化性能\"的优先级从8调整为4" << std::endl;taskHeap.decreaseKey(taskNodes[4], {4, "优化性能"});// 删除一个任务std::cout << " 删除任务\"编写文档\"" << std::endl;taskHeap.deleteNode(taskNodes[0]);// 按新的优先级处理任务std::cout << "\n按新优先级处理任务:" << std::endl;while (!taskHeap.isEmpty()) {std::cout << " 处理: " << taskHeap.extractMin() << std::endl;}} catch (const std::exception& e) {std::cerr << "发生错误: " << e.what() << std::endl;return 1;}return 0;
}
19.4 最大度数的界

斐波那契堆的效率很大程度上依赖于其节点的最大度数有一个较小的上界。这个上界与黄金比例有关。
19.4.1 度数界的证明
对于一个包含 n 个节点的斐波那契堆,任意节点的度数的上界为 O (log n)。更精确地说,如果 n ≥ 1,则任意节点的度数最多为⌊log_φ n⌋,其中 φ 是黄金比例(1+√5)/2 ≈ 1.618。
这个界限的证明基于斐波那契数的性质:对于度数为 k 的节点,其包含的后代数量至少为第 k+2 个斐波那契数。
19.4.2 斐波那契数与度数的关系
斐波那契数定义为:
- F₀ = 0
- F₁ = 1
- Fₖ = Fₖ₋₁ + Fₖ₋₂ (对于 k ≥ 2)
度数为 k 的节点至少有 Fₖ₊₂个后代(包括自身)。
度数为0
至少F₂=1个节点
度数为1
至少F₃=2个节点
度数为2
至少F₄=3个节点
度数为3
至少F₅=5个节点
度数为k
至少Fₖ₊₂个节点
19.4.3 实际意义
这个度数界限保证了斐波那契堆的 consolidate 操作能在 O (log n) 时间内完成,从而确保了抽取最小元素和删除操作的摊还时间复杂度为 O (log n)。
思考题
比较斐波那契堆与二叉堆、二项堆在各种操作上的时间复杂度,并分析各自的适用场景。
如何修改斐波那契堆的实现,使其支持最大堆而不是最小堆?
证明:在一个斐波那契堆中,包含 n 个节点的树的最大度数为 O (log n)。
实现一个基于斐波那契堆的 Dijkstra 算法,用于求解单源最短路径问题。
分析斐波那契堆在实际应用中的优缺点,为什么在很多编程语言的标准库中没有采用斐波那契堆?
本章注记
斐波那契堆由 Fredman 和 Tarjan 于 1984 年提出,是数据结构设计中的一个重要里程碑。它展示了摊还分析技术如何用于设计高效的数据结构。
尽管斐波那契堆在理论上具有优异的时间复杂度,但在实际应用中,由于其实现的复杂性和较高的常数因子,它并不总是最佳选择。在许多情况下,二项堆或甚至二叉堆可能表现得更好。
斐波那契堆的思想启发了其他高效数据结构的设计,如配对堆(Pairing Heap),它在实践中往往比斐波那契堆表现更好,同时保持了简单性。

斐波那契堆在算法设计中有着重要应用,特别是在图算法中,如用于实现高效的最小生成树算法和最短路径算法。
完整代码使用说明
为了使用本文实现的斐波那契堆,您需要:
- 将节点结构和类定义保存为 "fibonacci_heap.h"
- 将基本操作实现保存为 "fibonacci_heap.cpp"
- 将关键字减值和删除操作实现保存为 "fibonacci_heap_decrease_delete.cpp"
- 根据需要使用示例代码,如优先级队列或动态优先级调整示例
编译时,确保将所有源文件一起编译。例如,使用 g++:
g++ -std=c++11 fibonacci_heap.cpp fibonacci_heap_decrease_delete.cpp priority_queue_example.cpp -o fib_heap_example
总结
斐波那契堆是一种理论上非常高效的可合并堆数据结构,它的设计展示了如何通过巧妙的数据结构组织和摊还分析来获得优异的时间复杂度。虽然实现复杂,但它为许多算法问题提供了最优解,特别是那些需要频繁合并操作的场景。

通过本文的讲解和实现示例,希望读者能够深入理解斐波那契堆的工作原理,并能在实际应用中灵活运用这一强大的数据结构。