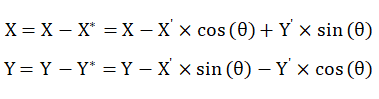视觉相机偏移补偿
一、二维转化的基本原理
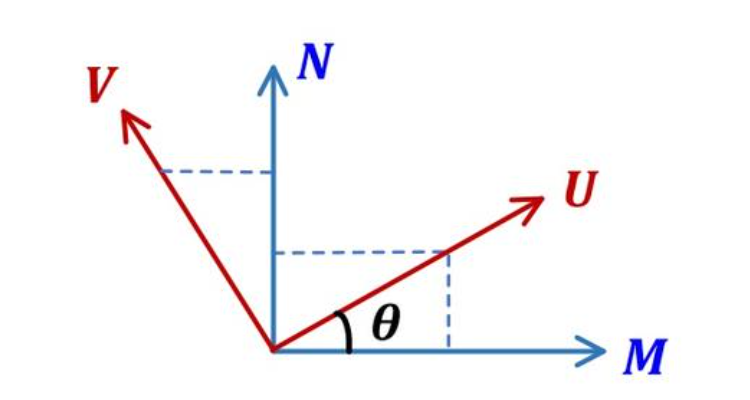
如下图所示:坐标系A中的坐标轴为M、N,进行逆时针旋转了θ度后,得到了新的坐标系B,B的坐标轴为U、V。坐标系B是由坐标系A旋转变化得到(逆时针为正,顺时针为负):
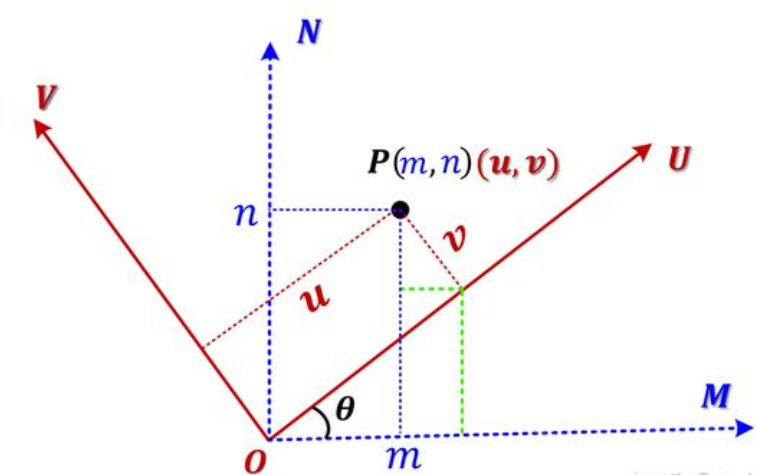
将空间中,需要拍照验证的物体设为点P,将P点对应分解到下列两个坐标系中:
根据上图中的几何关系可以两组坐标(m,n)和(u,v)的关系:
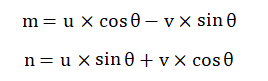
可知如果机器人或行走轴模组原坐标系为X、Y,旋转后的坐标为X’、Y’,可得下述关系:
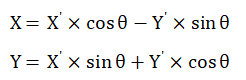
二、使用案例
当前2D相机的使用场景为抓完产品后进行拍照,就是下相机的模式,那么实际放置的点位公式为(X、Y、A为放置点位使用的坐标数据,X*,Y*,Z*为视觉相机给执行机构的偏移量)
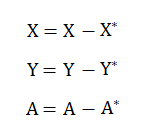
产品拍照方向与产品放置方向如下图所示:
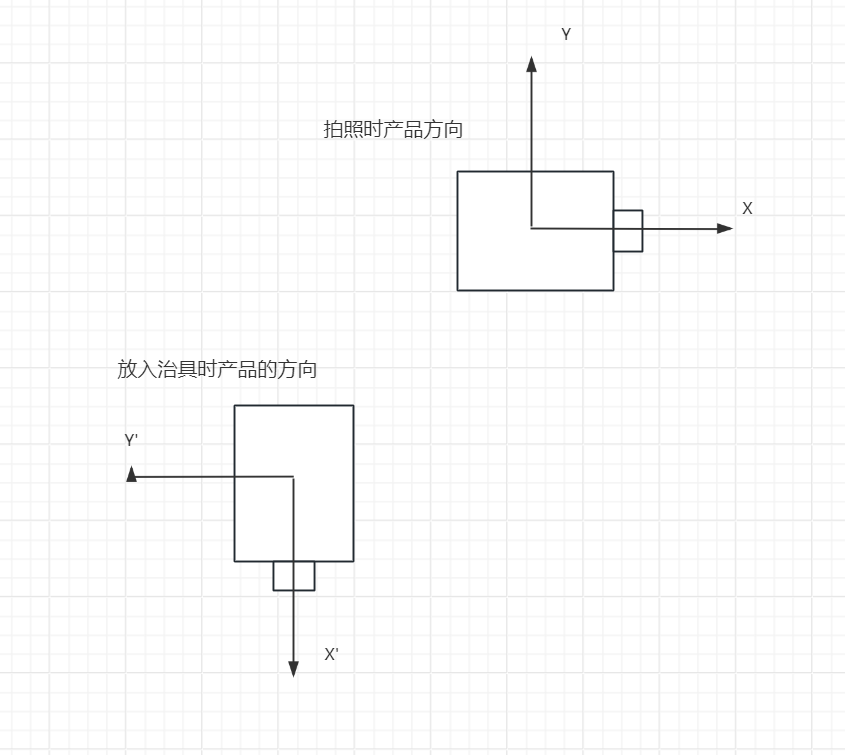
在理想状态治具与相机拍照位置没有水平和竖直上的偏差量时,坐标系做了顺时针旋转,角度θ为-90度。
先将相机偏移量进行转化:
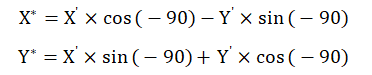
带入下相机公式得到实际对应的X,Y,A的坐标:
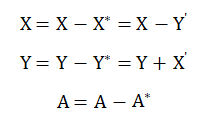
如相机与治具落位存在安装误差,找出θ角度,确认θ角度的正负号:
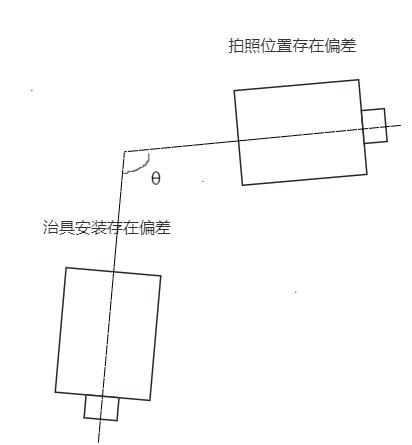
带入公式进行转化后为:
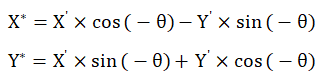
带入下相机公式为:
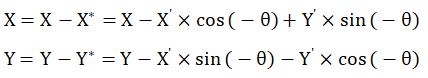
综上所述可得下相机模式2D相机旋转变化的通用公式为(X、Y为放置坐标点位当前位置坐标值,X’、Y’为相机给出的方向上的偏移量):