机器学习实战·第三章 分类(1)
一、MNIST
MNIST 是经典的手写数字数据集,含 6 万训练图和 1 万测试图,每张为 28×28 像素的灰度数字(0-9)。它是机器学习和深度学习的入门基准,常用于测试分类算法效果。
1.1下载MNIST数据集
import os
import numpy as np
from sklearn.datasets import fetch_openml# 设置下载路径
download_dir = "D:\\deskTop\\机器学习实战\\第三章"
os.makedirs(download_dir, exist_ok=True)# 下载 MNIST 数据集到指定路径
mnist = fetch_openml('mnist_784', version=1, data_home=download_dir, as_frame=False)# 将数据集划分为特征和标签
#X是个70000行,784列的二维数组。y是个70000个元素的一维数组,存储的是70000个值['5' '0' '4' ... '4' '5' '6']
X, y = mnist.data, mnist.target# 将标签转换为整数类型
y = y.astype(np.int8)# 可选:将数据保存为 NumPy 数组
np.save(os.path.join(download_dir, 'mnist_X.npy'), X)
np.save(os.path.join(download_dir, 'mnist_y.npy'), y)# 查看数据的形状和标签
print(f"数据集已保存到:{download_dir}")
print("数据形状:", X.shape)
print("标签形状:", y.shape)
fetch_mldata在 scikit-learn 0.20 版本后已被移除,改用fetch_openml替代。
fetch_openml('mnist_784')是获取 MNIST 数据集的新方式- 加载后的数据结构与原来类似,包含数据(
data)和标签(target)version=1确保获取的是原始格式的 MNIST 数据
1.2 抓取特征向量并显示
MNIST中每张图片是28×28像素,每个像素的强度从0(白色)到255(黑色)。因此每个图片共28×28=784个特征(像素)。将这些特征(像素)重新组成一个28×28的数组再通过Matplotlib显示出来。
# 导入matplotlib库,用于绘制图像
import matplotlib
# 从sklearn库中导入获取公开数据集的工具
from sklearn.datasets import fetch_openml
# 导入matplotlib的绘图模块,给它起个简单的别名plt
import matplotlib.pyplot as plt# 加载MNIST数据集(手写数字图片集)
# 'mnist_784':这是MNIST数据集的标准名称,784表示每张图片是28×28像素(28×28=784)
# version=1:指定使用第1版数据集,保证数据格式正确
# data_home:指定数据集在电脑中的存储路径(这里是你自己的路径)
# as_frame=False:表示让数据以数组形式返回,方便我们处理图像
mnist = fetch_openml('mnist_784', version=1, data_home="D:\\deskTop\\机器学习实战\\第三章", as_frame=False)# 从加载的数据集里提取图片数据和对应的标签
# X:存储所有图片的像素数据,每个图片被转换成了784个数字(28×28像素展开)
# y:存储每个图片对应的数字标签(0-9中的一个)
X, y = mnist.data, mnist.target# 从所有图片中选第10000张(计算机计数从0开始,所以10000是第10001张)
some_digit = X[10000]# 把784个数字重新变成28×28的矩阵(恢复成图片的原始尺寸)
some_digit_image = some_digit.reshape(28, 28)# 显示这张图片
# imshow():matplotlib中显示图像的函数
# cmap=matplotlib.cm.binary:用黑白颜色显示(手写数字适合黑白显示)
# interpolation='nearest':让图像边缘清晰,不模糊
plt.imshow(some_digit_image, cmap=matplotlib.cm.binary, interpolation='nearest')# 关闭图像的坐标轴(不需要显示x轴和y轴)
plt.axis('off')# 弹出窗口显示图片
plt.show()#显示标签
print(y[10000])

1.3 将训练集数据洗牌
# 导入numpy库(用于数值计算,这里用它生成随机序列)
import numpy as np# 生成0到59999的随机排列序列(共60000个数字)
# np.random.permutation(60000)会随机打乱0-59999的顺序,比如可能生成[3, 1, 4, 0, ..., 59998]这样的序列
# 这个序列就是我们用来打乱训练集的"随机索引"
shuffle_index = np.random.permutation(60000)# 根据随机索引重新排列训练集的特征和标签
# X[shuffle_index]:用随机索引重新排序图像数据,让原来的顺序被打乱
# y[shuffle_index]:标签也用同样的随机索引打乱,保证每个图像和它的标签对应关系不变
# 假设原来X[0]对应y[0],打乱后X[新位置]依然对应y[新位置]
X_train, y_train = X[shuffle_index], y[shuffle_index]
为什么要打乱数据?
很多机器学习模型(比如梯度下降)在训练时对数据顺序敏感,如果数据按固定顺序排列(比如先全是 0,再全是 1),模型可能学不好。打乱后数据分布更均匀,模型能更稳定地学习。代码的核心作用
- 生成一组 "随机序号"(比如把 60000 个样本的顺序彻底打乱)
- 用这组序号重新排列图像数据(X)和标签(y),确保每个图像和它的标签始终配对(不会张冠李戴)
举个小例子
假设原来数据顺序是:X=[图0, 图1, 图2],y=[0, 1, 2]
生成的随机索引是[2, 0, 1]
打乱后变成:X_train=[图2, 图0, 图1],y_train=[2, 0, 1](图像和标签依然对应)这样处理后,训练集的顺序被随机化,能帮助模型更好地学习通用规律,避免受原始数据顺序的干扰。
二、训练二元分类器
# 从sklearn库中导入获取公开数据集的工具
from sklearn.datasets import fetch_openml
# 导入处理数组和随机数的工具库
import numpy as np
# 导入SGD分类器(一种快速的机器学习分类模型)
from sklearn.linear_model import SGDClassifiermnist = fetch_openml('mnist_784', version=1, data_home="D:\\deskTop\\机器学习实战\\第三章", as_frame=False)X, y = mnist.data, mnist.target# 划分训练集和测试集(MNIST标准划分方式)
# 前60000张作为训练集(让模型学习),后10000张作为测试集(检验模型效果)
#这里的X_train是个二维数组(60000, 784)、X_test (10000, 784) 、y_train(60000,) 、y_test(10000,)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]shuffle_index = np.random.permutation(60000)X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]# 定义二分类任务:判断一张图片"是不是数字5"
# 把原始标签转换成True/False(布尔值)
# y_train_5:训练集中的标签,是5就为True,不是5就为False
y_train_5 = (y_train == '5')
# y_test_5:测试集中的标签,同样用True/False表示是否为5
y_test_5 = (y_test == '5')# 创建SGD分类器实例
# random_state=42:固定随机种子,让每次运行结果一致(方便调试)
sgd_clf = SGDClassifier(random_state=42)# 训练模型:让模型学习如何区分"5"和"非5"
# 用训练集的图片(X_train)和对应标签(y_train_5)进行训练
sgd_clf.fit(X_train, y_train_5)# 选一个样本图片来测试模型(这里选第10000张图片)
some_digit = X[10000]# 用训练好的模型预测:这张图片是不是5?
# 输出结果是[False]表示模型认为不是5,[True]表示认为是5
print(sgd_clf.predict([some_digit]))#输出X[10000]这个数字
print(y_train[10000])
2.1 性能考核
2.1.1 使用交叉验证测量精度
机器学习中的交叉验证(Cross-Validation) 是一种评估模型性能的统计方法,通过多次划分训练数据和验证数据,减少因单次数据划分带来的随机性影响,从而更可靠地估计模型在 unseen(未见过)数据上的泛化能力。
核心思想
将原始训练数据集分为两部分:
- 训练集(Training Set):用于模型训练。
- 验证集(Validation Set):用于评估模型在训练过程中的性能,帮助调整超参数或选择模型。
通过多次重复 “划分 - 训练 - 验证” 的过程,取多次评估结果的平均值作为最终性能指标,降低数据划分偶然性的影响。
常见交叉验证方法
K 折交叉验证(K-Fold Cross-Validation)
- 将训练集平均分为
K个互斥的子集(称为 “折”,Fold)。- 每次用
K-1个折作为训练集,剩余 1 个折作为验证集,重复K次(确保每个折都做过验证集)。- 最终性能为
K次验证结果的平均值。- 优点:充分利用数据,结果稳定;缺点:计算成本随
K增加而提高(常用K=5或10)。分层 K 折交叉验证(Stratified K-Fold)
- 针对分类问题,确保每个折中各类别的样本比例与原始训练集一致(避免某一折中类别失衡)。
- 例如:二分类问题中原始数据正负样本比例为 3:1,每个折中也保持 3:1。
留一法(Leave-One-Out,LOO)
- 极端情况的 K 折交叉验证(
K = 样本总数)。- 每次留 1 个样本作为验证集,其余全部作为训练集,重复
N次(N为样本数)。- 优点:结果稳定(无随机划分);缺点:计算量极大(适用于小数据集)。
随机拆分交叉验证(Shuffle-Split Cross-Validation)
- 多次随机将数据拆分为训练集和验证集(比例可自定义,如 7:3),重复指定次数(如 10 次)。
- 优点:灵活,可控制训练集 / 验证集比例;缺点:可能有样本重复出现在验证集中。
在本例中使用三折叠的方式,也就是将训练数据平均分为三个互斥的子集,每次使用两个最为训练集一个作为验证集。
from sklearn.datasets import fetch_openml
import numpy as np
from sklearn.linear_model import SGDClassifier
# 导入交叉验证评分函数,用于评估模型性能
from sklearn.model_selection import cross_val_scoremnist = fetch_openml('mnist_784', version=1, data_home="D:\\deskTop\\机器学习实战\\第三章", as_frame=False)X, y = mnist.data, mnist.targetX_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]shuffle_index = np.random.permutation(60000)X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]y_train_5 = (y_train == '5')
y_test_5 = (y_test == '5')sgd_clf = SGDClassifier(random_state=42)sgd_clf.fit(X_train, y_train_5)# 使用交叉验证评估模型性能
# 参数说明:
# - sgd_clf:要评估的模型
# - X_train:训练集特征
# - y_train_5:训练集标签
# - cv=3:采用3折交叉验证(将训练集分为3份,轮流作为验证集)
# - scoring='accuracy':评估指标为准确率(正确预测的样本比例)
# 输出:3次验证的准确率结果(数组形式)
print(cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring='accuracy'))
局限性:MNIST 数据集中,“5” 的样本占比约 10%(60000 训练集中约 5421 个 “5”)。即使模型简单地将所有样本预测为 “非 5”,也能达到约 90% 的准确率。此时高准确率并不能反映模型的真实能力(无法识别 “5”)。
假设有一个模型,它不做任何学习,对所有图片都无脑预测为 “不是 5”(即不管输入是什么,输出都是 “非 5”)。
此时:
(正确预测的样本数)÷(总样本数)= 54579 ÷ 60000 ≈ 90.97%
- 对于 54579 张 “非 5” 图片:模型预测正确(因为确实不是 5)
- 对于 5421 张 “5” 图片:模型预测错误(把 5 当成了非 5)
这个 “摆烂” 模型完全无法识别 “5”(所有 “5” 都被误判),但准确率却高达 90% 以上。这显然很荒谬 —— 高准确率只是因为 “非 5” 的样本占绝大多数,模型哪怕乱猜 “非 5” 也能蒙对大多数。
这说明:当数据类别不平衡(某一类占比极高)时,准确率会 “欺骗” 我们,让我们误以为模型很好,但实际上模型可能完全没学会核心任务(比如这里的 “识别 5”)。
2.1.2 混淆矩阵
混淆矩阵是评估分类模型性能的基础工具,它用一个表格清晰展示模型预测结果与真实标签的匹配情况,能直观反映模型的错误类型(比如 “把 A 错当成 B” 还是 “漏检了 A”),简单的说混淆矩阵其实是模型的成绩单。
以二分类问题(比如 “判断是否为5”)为例,混淆矩阵是一个 2×2 的表格,包含 4 种核心结果:
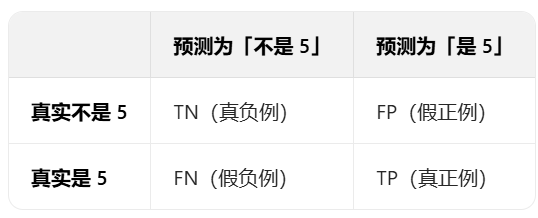
- TP:模型猜对了(实际是正类,预测也是正类)
- FP:模型瞎报了(实际是负类,却预测为正类)
- FN:模型漏检了(实际是正类,却预测为负类)
- TN:模型正确排除(实际是负类,预测也是负类)
# 导入需要的工具包
# 从sklearn获取公开数据集的工具
from sklearn.datasets import fetch_openml
# 处理数组的工具
import numpy as np
# 导入SGD分类器(一种快速的机器学习模型)
from sklearn.linear_model import SGDClassifier
# 导入交叉验证相关工具:评估模型和获取预测结果
from sklearn.model_selection import cross_val_score, cross_val_predict
# 导入混淆矩阵工具:展示模型的预测对错情况
from sklearn.metrics import confusion_matrix# 加载MNIST手写数字数据集
# 这个数据集包含70000张手写数字图片,每张图片是28×28像素
# as_frame=False表示返回的是数组格式(不是表格格式)
mnist = fetch_openml('mnist_784', version=1, data_home="D:\\deskTop\\机器学习实战\\第三章", as_frame=False)# 拆分数据:X是图片的像素数据,y是对应的数字标签
# X是70000行784列的二维数组(70000张图,每张图784个像素值)
# y是70000个元素的一维数组(每个元素是图片对应的数字,比如'5'、'0'等字符串)
X, y = mnist.data, mnist.target# 划分训练集和测试集
# 前60000张图片和标签作为训练集(让模型学习)
# 后10000张作为测试集(之后用来检验模型效果)
# X_train:(60000, 784)的二维数组(训练图片)
# X_test:(10000, 784)的二维数组(测试图片)
# y_train:(60000,)的一维数组(训练图片的真实数字)
# y_test:(10000,)的一维数组(测试图片的真实数字)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]# 生成打乱顺序的索引:0到59999的随机排列
# 作用是打乱训练集的顺序,避免模型学到数据的顺序规律(比如前面都是0,后面都是1)
shuffle_index = np.random.permutation(60000)# 按照随机索引重新排列训练集的图片和标签
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]# 定义二分类任务:只判断图片是不是数字"5"
# 生成新的标签:如果原始标签是'5',就记为True(是5),否则记为False(不是5)
# y_train_5:训练集的二分类标签(60000个布尔值)
# y_test_5:测试集的二分类标签(10000个布尔值)
y_train_5 = (y_train == '5')
y_test_5 = (y_test == '5')# 创建SGD分类器实例
# random_state=42:固定随机数种子,让每次运行结果一样(方便调试)
sgd_clf = SGDClassifier(random_state=42)# 用训练集训练模型
# 让模型学习:从图片像素(X_train)中识别出哪些是5(y_train_5为True),哪些不是
sgd_clf.fit(X_train, y_train_5)# 用交叉验证获取模型的预测结果
# 把训练集分成3份,轮流用2份训练、1份预测,最后得到所有样本的预测结果
# y_train_pred:60000个布尔值的一维数组(模型认为每个样本是不是5)
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)# 打印混淆矩阵:展示模型预测的"对错明细"
# 输入真实标签(y_train_5)和预测标签(y_train_pred)
# 输出一个2×2的表格,直观显示模型哪里对了、哪里错了
print(confusion_matrix(y_train_5, y_train_pred))
- TP = 4193(真实是 5,模型也预测是 5 → 猜对的 5)
- FP = 773(真实不是 5,模型预测是 5 → 误报成 5 的非 5 样本)
- FN = 1228(真实是 5,模型预测不是 5 → 漏检的 5)
- TN = 53806(真实不是 5,模型也预测不是 5 → 正确排除的非 5 样本)
但是一个完美的分类器只有真正类和真负类,也就是只有对角线上存在数据。
2.1.3 精度和召回率
在分类任务中,精度(Precision)也称为精确率、查准率,用于衡量模型预测为正类的样本中,真正是正类的比例 。
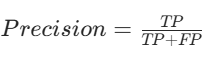
- TP(True Positive,真正例):真实类别为正类,模型预测也为正类的样本数量。比如在手写数字识别中,图片真实数字是 “5”,模型也预测为 “5” 的样本数量。
- FP(False Positive,假正例):真实类别为负类,模型却预测为正类的样本数量。例如图片真实数字不是 “5”,但模型预测为 “5” 的样本数量。
举个例子,假设模型预测了 100 个样本为 “5”,其中实际是 “5” 的有 80 个(TP = 80),不是 “5” 却被误判为 “5” 的有 20 个(FP = 20),那么精度为:
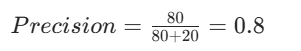
即模型预测为 “5” 的样本中,真正是 “5” 的比例为 80% 。
召回率(Recall),也叫查全率,是评估分类模型性能的重要指标,尤其在关注 “不能漏掉正例” 的场景(如疾病筛查、安全检测)中非常关键。
对于 “识别 5” 这类二分类任务,召回率公式为:
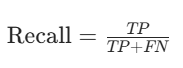
- TP(True Positive):真实是正例(比如真实是 5),模型也预测为正例(模型猜对是 5)
- FN(False Negative):真实是正例(真实是 5),但模型预测为负例(模型漏检、没认出是 5)
召回率回答的问题是:“所有真实的正例里,模型成功找出来多少?”
| 指标 | 关注问题 | 公式 | 场景侧重 |
|---|---|---|---|
| 召回率(Recall) | 真实正例被模型 “找全” 了吗? | TP/FN+TP | 不能漏检(如疾病筛查、安防) |
| 精确率(Precision) | 模型预测的正例 “真的对吗?” | TP/FP+TP | 不能误报(如垃圾邮件过滤) |
# 从sklearn的评估指标工具中导入精确率和召回率的计算函数
# precision_score:用于计算精确率(查准率)
# recall_score:用于计算召回率(查全率)
from sklearn.metrics import precision_score, recall_score# ...(省略前面的数据加载、预处理和模型训练代码)# 计算并打印精确率(Precision)
# 参数说明:
# y_train_5:真实标签(布尔值数组),True表示真实是5,False表示真实不是5
# y_train_pred:模型预测结果(布尔值数组),True表示模型认为是5,False表示模型认为不是5
# 精确率公式:TP / (TP + FP)
# TP:真实是5且模型预测是5(猜对的5)
# FP:真实不是5但模型预测是5(误判为5的非5样本)
# 含义:模型预测为"是5"的样本中,真正是5的比例(反映模型"不乱报"的能力)
print(precision_score(y_train_5, y_train_pred))# 计算并打印召回率(Recall)
# 参数说明同上,使用相同的真实标签和预测结果
# 召回率公式:TP / (TP + FN)
# TP:同上(猜对的5)
# FN:真实是5但模型预测不是5(漏检的5样本)
# 含义:所有真实是5的样本中,被模型成功识别出来的比例(反映模型"不漏检"的能力)
print(recall_score(y_train_5, y_train_pred))
2.1.4F1分数
F1 分数(F1-Score)是一个综合指标,用来平衡合精确率(Precision) 和召回率(Recall) 的表现,避免单一指标的片面性。
当精确率和召回率发生冲突时(比如一个高一个低),F1 分数能给出一个平衡的评价。比如:
- 模型 A:精确率 90%,召回率 60%(太保守,漏检多)
- 模型 B:精确率 60%,召回率 90%(太激进,误报多)
F1 分数能客观比较哪个模型整体表现更好
F1 分数是精确率和召回率的调和平均数:

- 取值范围:0~1(越接近 1,说明精确率和召回率都高,模型越均衡)
- 特点:对精确率和召回率 “一视同仁”,如果其中一个很低,F1 分数也会很低。
from sklearn.metrics import f1_score......#输出F1分数
print(f1_score(y_train_5, y_train_pred))
在很多实际场景中,我们需要根据具体需求优先关注精确率(Precision)或召回率(Recall),而不是一味追求两者平衡的 F1 分数。这取决于业务中 “误判” 和 “漏判” 的代价哪个更高。
当 “把不是目标的样本错判为目标” 的代价很高时,需要优先保证精确率(即 “模型说‘是’的,尽量真的是”)。
当 “把目标样本漏判为非目标” 的代价很高时,需要优先保证召回率(即 “所有真的是目标的,尽量都被模型找出来”)。
- 垃圾邮件过滤:如果把正常邮件(非垃圾)误判为垃圾邮件(模型说 “是垃圾”),用户可能错过重要邮件,代价很高。此时更关注精确率 —— 宁可漏判一些垃圾邮件(让少量垃圾进 inbox),也不能误删正常邮件。
- 肿瘤筛查(初步检测):如果用 AI 初步筛选 “疑似癌症”,如果把健康人误判为 “疑似癌症”(模型说 “是癌症”),会导致用户恐慌、不必要的进一步检查(耗时耗钱),此时需要高精确率 —— 模型标记的 “疑似” 必须尽可能真的有问题。
- 推荐系统(如奢侈品推荐):如果给用户推荐不相关的商品(模型说 “用户会买” 但实际不会),会浪费流量、降低用户体验,此时需要精确率 —— 推荐的东西必须尽可能贴合用户需求。
- 犯罪嫌疑人识别:如果漏掉了真正的嫌疑人(模型说 “不是嫌疑人” 但实际是),可能导致罪犯逃脱,代价极高。此时更关注召回率 —— 宁可错判一些无辜者(精确率低一点),也不能漏掉真凶。
- 癌症确诊(最终诊断):如果把真正的癌症患者漏判为 “健康”(模型说 “不是癌症”),会延误治疗,甚至危及生命。此时必须优先保证召回率 —— 哪怕把很多健康人误判为 “疑似”(后续再人工复核),也不能漏掉一个真患者。
- 网络攻击检测:如果漏掉了真正的攻击行为(模型说 “不是攻击” 但实际是),可能导致系统被入侵、数据泄露。此时需要高召回率 —— 宁可误报一些正常操作(后续人工排查),也不能放过任何潜在攻击。
2.1.5 精度/召回率权衡
SGDClassifier 识别 MNIST 中的 "5" 时,会给 784 个像素分别分配权重(比如 "5" 特有的像素位置权重为正),将图片像素值与对应权重相乘后求和,再和一个阈值比较 —— 超过阈值就判定为 "5",否则不是,就像根据关键特征打分后判断是否达标。阈值越高,模型判定为 “5” 的标准就越严格。比如原来 50 分就能算 “是 5”,现在阈值提到 80 分 —— 只有那些像素特征特别符合 “5” 的图片(总分超 80)才会被认成 5,其他哪怕有点像 5 但分数不够的,都会被归为 “不是 5”。
结果就是:模型说 “是 5” 的图片里,真正是 5 的比例(精度)会提高,但很多真正的 5 可能因为分数不够被漏掉(召回率会下降)。
# 导入从开放数据源获取数据集的工具
from sklearn.datasets import fetch_openml
# 导入数值计算库,用于处理数组和矩阵
import numpy as np
# 导入绘图库,用于可视化图像(本代码未实际绘图,可用于扩展)
import matplotlib.pyplot as plt
# 导入随机梯度下降分类器模型
from sklearn.linear_model import SGDClassifier# 获取MNIST手写数字数据集
# 'mnist_784'是数据集标识,包含70000张28x28像素的手写数字图片(展平为784维特征)
# version=1指定数据集版本,data_home指定下载路径,as_frame=False返回numpy数组格式
mnist = fetch_openml('mnist_784', version=1, data_home="D:\\deskTop\\机器学习实战\\第三章", as_frame=False)# 拆分特征数据和标签:
# X:所有图片的像素数据(70000行×784列),每行是一张图片的784个像素值
# y:所有图片对应的数字标签(70000个元素),以字符串形式存储(如'5'、'3')
X, y = mnist.data, mnist.target # 划分训练集和测试集:
# 前60000个样本作为训练集(模型学习用),后10000个作为测试集(模型评估用)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]# 设置随机种子,确保每次运行时随机操作的结果完全一致(可复现性)
np.random.seed(42)
# 生成0到59999的随机打乱的索引序列,用于打乱训练集顺序
# 打乱数据能避免模型学习到样本顺序的无关规律,提高模型泛化能力
shuffle_index = np.random.permutation(60000)# 使用随机索引重新排列训练集的特征和标签(保持样本与标签的对应关系)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]# 构建二分类任务标签:判断样本是否为数字5
# y_train_5是布尔数组,True表示对应样本是5,False表示不是5
y_train_5 = (y_train == '5')
# 同样处理测试集标签,用于后续模型评估
y_test_5 = (y_test == '5')# 创建SGD分类器实例,random_state=42固定随机种子,保证训练过程可复现
sgd_clf = SGDClassifier(random_state=42)# 用训练集训练模型,学习如何区分"是5"和"不是5"
sgd_clf.fit(X_train, y_train_5)# 找到训练集中所有标签为'5'的样本索引
# np.where返回满足条件的索引位置,[0]提取索引数组(因为返回格式是元组)
five_indices = np.where(y_train == '5')[0]
# 将索引转换为列表并打印,展示所有数字5在训练集中的位置
print(five_indices.tolist())# 从训练集中选取索引为51868的样本(已知是数字5,从上面的索引列表中选取)
some_digit = X_train[51868]# 计算该样本的决策分数:
# 1. 先用reshape(1, -1)将一维数组转为二维数组(1个样本 × 784个特征),符合模型输入要求
# 2. decision_function返回模型对该样本的评分(正数表示模型认为是5,负数表示认为不是5)
y_scores = sgd_clf.decision_function(some_digit.reshape(1, -1))# 打印决策分数
print(y_scores)
在这个判断是否为 5 的二分类任务里,
decision_function输出分数越高,模型越笃定该样本是数字 5 ,分数高就代表模型对 “是 5” 这个判断的信心很足~。但是究竟分数多低就表示信心不足了呢?换言之,如何决定使用什么样的阈值呢?
绘制精确率-召回率-阈值曲线
# 导入需要的库
# fetch_openml用于获取公开数据集,这里用于加载MNIST手写数字数据集
from sklearn.datasets import fetch_openml
# numpy用于数值计算和数组操作
import numpy as np
# matplotlib.pyplot用于数据可视化
import matplotlib.pyplot as plt
# SGDClassifier是随机梯度下降分类器,适用于大规模数据集
from sklearn.linear_model import SGDClassifier
# cross_val_score用于交叉验证评分,cross_val_predict用于交叉验证预测
from sklearn.model_selection import cross_val_score, cross_val_predict
# precision_recall_curve用于计算精确率、召回率和阈值的关系
from sklearn.metrics import precision_recall_curve# 设置matplotlib支持中文显示
# 解决中文显示为方框的问题
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
# 解决负号显示异常的问题
plt.rcParams["axes.unicode_minus"] = False# 获取MNIST数据集
# 'mnist_784'是数据集名称,包含70000张28x28像素的手写数字图片
# version=1指定数据集版本
# data_home指定数据集下载后保存的本地路径
# as_frame=False表示返回numpy数组格式而非DataFrame
mnist = fetch_openml('mnist_784', version=1, data_home="D:\\deskTop\\机器学习实战\\第三章", as_frame=False)# 提取特征数据和标签
# X包含所有图像的像素数据,形状为(70000, 784),每行代表一张图片的784个像素(28×28)
# y包含所有图像对应的标签,形状为(70000,),存储的是0-9的字符串形式数字
X, y = mnist.data, mnist.target# 划分训练集和测试集
# MNIST数据集默认前60000个样本为训练集,后10000个为测试集
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]# 打乱训练集顺序
# 生成0-59999的随机排列索引,用于打乱训练集,避免数据顺序对模型产生影响
shuffle_index = np.random.permutation(60000)
# 根据随机索引重新排列训练集的特征和标签
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]# 创建二分类标签:是否为数字5
# 将原始标签转换为布尔值,True表示该样本是数字5,False表示不是
# 这样就将问题转化为"是5"和"不是5"的二分类问题
y_train_5 = (y_train == '5') # 训练集的二分类标签
y_test_5 = (y_test == '5') # 测试集的二分类标签# 初始化并训练SGD分类器
# SGDClassifier使用随机梯度下降算法,适合处理大型数据集
# random_state=42设置随机种子,保证结果可复现
sgd_clf = SGDClassifier(random_state=42)
# 使用训练集训练模型,学习如何区分数字5和非5
sgd_clf.fit(X_train, y_train_5)# 使用交叉验证获取决策分数
# cross_val_predict进行交叉验证,并返回每个样本的决策分数
# cv=3表示3折交叉验证,将训练集分成3份,轮流用2份训练1份验证
# method="decision_function"表示返回决策函数的值(而非预测类别),用于后续计算阈值
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5,cv=3, method="decision_function"
)# 输出部分决策分数
# 决策分数表示模型认为样本属于正类(数字5)的置信度,值越高越可能是5
# 只输出前10个,避免输出过多
print("部分决策分数:", y_scores[:10])# 计算不同阈值下的精确率和召回率
# precision_recall_curve函数会计算所有可能阈值对应的精确率和召回率
# 精确率(Precision):预测为5的样本中真正是5的比例
# 召回率(Recall):所有真正是5的样本中被成功预测为5的比例
# 阈值(Threshold):用于判断样本属于正类或负类的临界值
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)# 定义绘制精确率-召回率-阈值曲线的函数
def plot_precision_recall_curve(precisions, recalls, thresholds):# 创建一个10x6英寸的图形plt.figure(figsize=(10, 6))# 绘制精确率曲线,蓝色虚线,标签为"精确率(Precision)"plt.plot(thresholds, precisions[:-1], 'b--', label='精确率(Precision)')# 绘制召回率曲线,绿色实线,标签为"召回率(Recall)"plt.plot(thresholds, recalls[:-1], 'g-', label='召回率(Recall)')# 设置x轴标签plt.xlabel('阈值(Threshold)')# 设置y轴标签plt.ylabel('值')# 设置图表标题plt.title('精确率和召回率随阈值变化的曲线')# 显示图例,自动选择最佳位置plt.legend(loc='best')# 设置y轴范围,稍微超过1使图形更美观plt.ylim([0, 1.05])# 添加网格线,透明度0.3plt.grid(True, alpha=0.3)# 调用函数绘制曲线
plot_precision_recall_curve(precisions, recalls, thresholds)
# 显示图形
plt.show()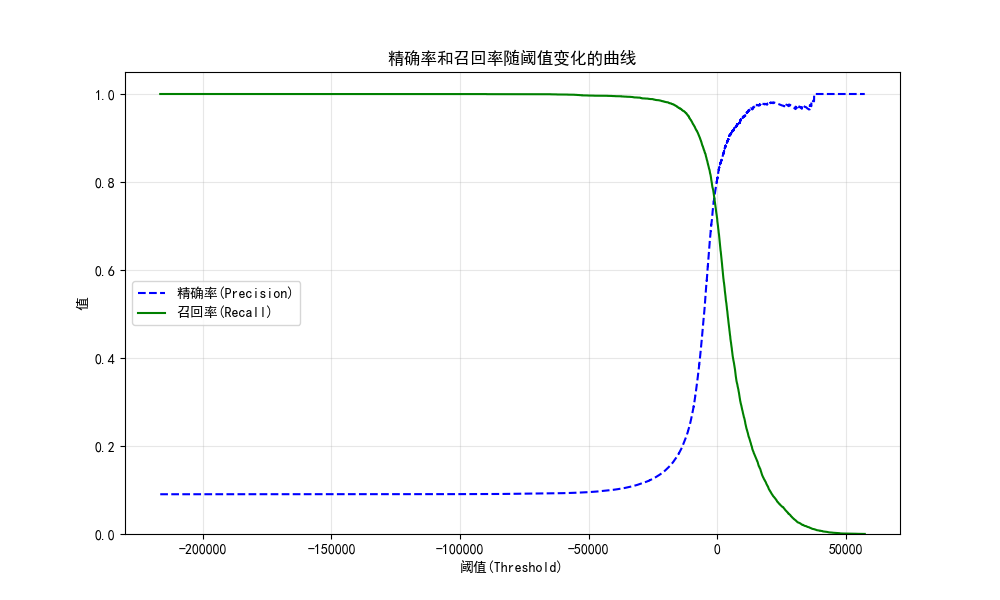
1. 先理解「阈值(Threshold)」:模型的 “5 判定标准”
模型判断一个手写数字是不是 5 时,会先算一个 **“分数”**(由
SGDClassifier的decision_function输出)。
- 分数越高 → 模型越觉得这是 5;
- 分数越低 → 模型越觉得这不是 5。
阈值就是你定的一条 “及格线”:
- 分数 ≥ 阈值 → 模型说 “是 5”;
- 分数 < 阈值 → 模型说 “不是 5”。
2. 绿色线(召回率):「真 5 被找全了吗?」
召回率的意思是:所有真正是 5 的数字里,有多少被模型找出来了。
当阈值特别小(比如图最左边,阈值 =-200000):
模型会 “不管三七二十一,觉得谁都像 5”,几乎所有真 5 都会被选中 → 召回率接近 1(绿色线贴到最顶)。
但代价是:很多不是 5 的数字(比如 2、3、7)也会被误判成 5 → 精确率会特别低(蓝色线贴到最底)。当阈值特别大(比如图最右边,阈值 = 50000):
模型会 “特别挑剔,只有超级像 5 的才敢说是 5”,几乎不会误判 → 精确率接近 1(蓝色线贴到最顶)。
但代价是:很多真正的 5 会因为分数不够,被模型漏掉 → 召回率会特别低(绿色线掉到最底)。3. 蓝色线(精确率):「模型说 “是 5” 的,真的是 5 吗?」
精确率的意思是:模型说 “是 5” 的数字里,有多少真的是 5。
当阈值小(左):
模型 “乱认 5” → 精确率低(蓝色线低),但召回率高(绿色线高)。当阈值大(右):
模型 “谨慎认 5” → 精确率高(蓝色线高),但召回率低(绿色线低)。4. 核心规律:「鱼和熊掌不可兼得」
调整阈值时,召回率和精确率永远反向变化:
- 想找全所有真 5(高召回率)→ 必须接受误判(低精确率);
- 想让模型说 “是 5” 的都真的是 5(高精确率)→ 必须接受漏掉一些真 5(低召回率)。
5. 怎么选阈值?看你的需求!
如果是「找错题」场景(比如老师想找出所有学生写的 5 分步骤批改):
宁愿误判一些非 5 为 5,也不想漏掉真 5 → 选低阈值(往左边调),优先保召回率。如果是「自动分类归档」场景(比如把数字 5 单独放进一个文件夹,错放会打乱分类):
宁愿漏掉一些真 5,也不想把非 5 放进来 → 选高阈值(往右边调),优先保精确率。
