leetcode2090：半径为K的子数组平均值（定长滑动窗口）

LeetCode 2090. 半径为 k 的子数组平均值，【难度：中；通过率：45.7%】，这道题要求我们计算一个“移动平均值”，和上一题“ leetcode1652：拆炸弹（环形+定长滑动窗口）”思路类似，主要需要注意的仍旧是处理 边界条件

一、 题目描述

给你一个下标从 0 开始的数组 nums，数组中有 n 个整数，另给你一个整数 k

k 半径子数组 的 平均值 是指：以 i 为中心，半径为 k 的子数组（即从 i-k 到 i+k 的所有元素）的整数平均值。如果 i 的任一边没有 k 个元素，那么 k 半径子数组平均值视为 -1

你需要计算一个长度为 n 的数组 avgs，其中 avgs[i] 是 nums 中以 i 为中心的子数组的平均值

示例:

输入: nums = [7,4,3,9,1,8,5,2,6], k = 3
输出: [-1,-1,-1,5,4,4,-1,-1,-1]

解释：

• avg[0]、avg[1] 和 avg[2] 是 -1 ，因为在这几个下标前的元素数量都不足 k 个
• 中心为下标 3 且半径为 3 的子数组的元素总和是：7 + 4 + 3 + 9 + 1 + 8 + 5 = 37
  使用截断式 整数除法，avg[3] = 37 / 7 = 5
• 中心为下标 4 的子数组，avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4
• 中心为下标 5 的子数组，avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4
• avg[6]、avg[7] 和 avg[8] 是 -1 ，因为在这几个下标后的元素数量都不足 k 个

---

二、 核心思路：定长滑动窗口

这个问题的核心在于，对于每个有效的中心点 i，我们都需要计算一个固定长度为 2k + 1 的子数组的和。这正是定长滑动窗口算法的用武之地

我们的策略如下：

1. 确定有效中心点范围：一个索引 i 要能成为窗口中心，必须满足 i-k >= 0 且 i+k < n。这意味着 i 的范围是 [k, n - 1 - k]。所有在这个范围之外的索引，其平均值都为 -1
2. 处理边界情况：如果窗口大小 2k + 1 大于整个数组的长度 n，那么没有任何一个位置能形成完整的窗口，可以直接返回一个全为 -1 的数组
3. 初始化第一个窗口：计算出第一个有效窗口（中心在 k，范围是 [0, 2k]）的总和
4. 滑动窗口：从中心点 k+1 开始，窗口向右滑动。每次滑动，我们通过 O(1) 的操作来更新窗口和：
   • sum = sum - (滑出窗口的左侧元素) + (滑入窗口的右侧元素)
5. 计算平均值：在每次滑动后，用更新后的 sum 计算平均值并存入结果数组
6. 防止溢出：由于 sum 可能很大，使用 long 类型来存储是明智的选择

---

三、 代码实现与深度解析

class Solution {public int[] getAverages(int[] nums, int k) {int n = nums.length;int windowSize = 2 * k + 1; // 窗口的固定大小int[] avgs = new int[n];Arrays.fill(avgs, -1); // 1. 预先将所有结果填充为 -1// 2. 处理边界情况：窗口大小超过数组长度if (windowSize > n) {return avgs;}long currentSum = 0L; // 使用 long 防止整数溢出// 3. 初始化第一个有效窗口（中心在 k，范围是 [0, 2k]）for (int i = 0; i < windowSize; i++) {currentSum += nums[i];}// 计算第一个有效中心的平均值avgs[k] = (int) (currentSum / windowSize);// 4. 开始滑动窗口// 窗口的中心从 k+1 移动到 n-1-kfor (int i = k + 1; i <= n - 1 - k; i++) {// 窗口向右滑动一格// i 是新中心，i-k-1 是滑出窗口的元素索引// i+k 是滑入窗口的元素索引int leftElementIndex = i - k - 1;int rightElementIndex = i + k;currentSum = currentSum - nums[leftElementIndex] + nums[rightElementIndex];// 计算新中心的平均值avgs[i] = (int) (currentSum / windowSize);}return avgs;}
}

提交结果：

---

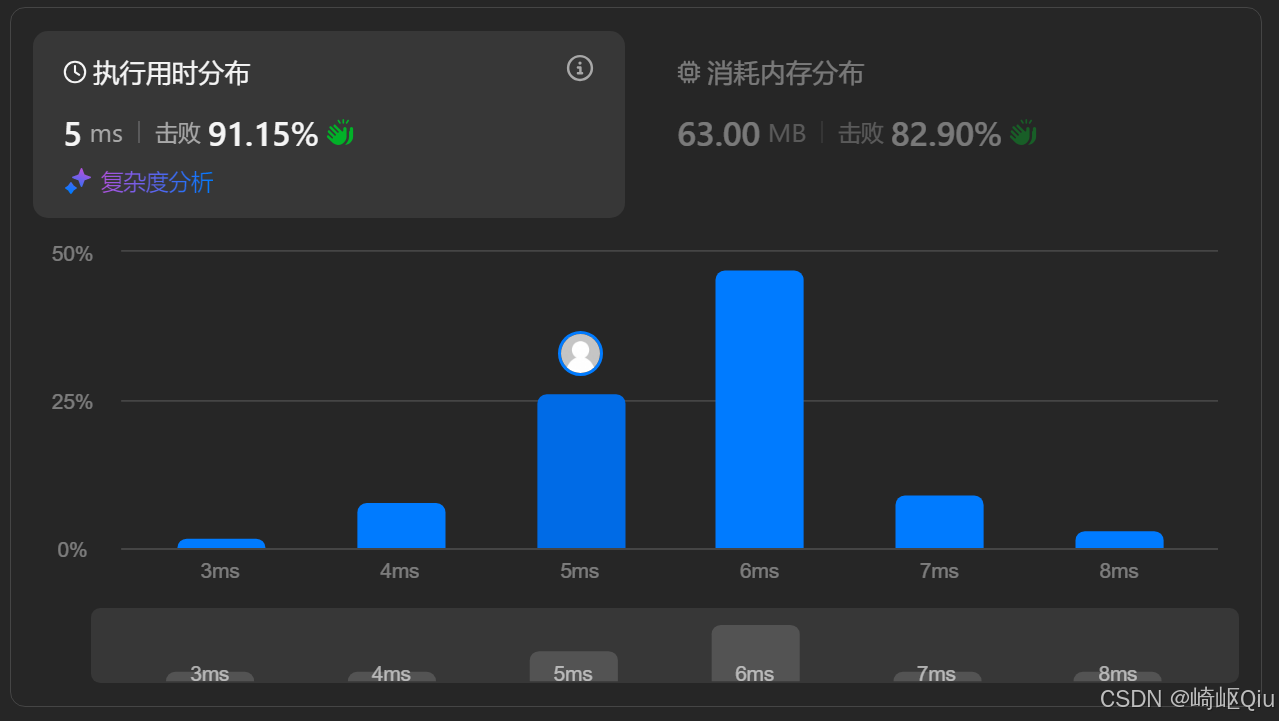
四、 关键点与复杂度分析

• 窗口大小：2k + 1 是本题滑动窗口的固定大小
• 有效中心范围：[k, n - 1 - k] 是能够形成完整窗口的中心点索引范围。理解这个范围是正确处理边界的关键
• O(1) 更新：currentSum = currentSum - old + new; 是滑动窗口算法效率的核心，它避免了每次都重新计算整个窗口的和
• 时间复杂度：O(N) 只需要遍历一次数组来初始化和滑动窗口
• 空间复杂度：O(N) 或 O(1) 如果计入返回的 avgs 数组，则为 O(N)；如果不计入，则只使用了常数个额外变量，为 O(1)