数据分析思维(六)|循环/闭环思维
循环/闭环思维
1、概念
在很多的分析场景下,我们需要按照一套流程反复分析,而不是进行一次性的分析,也就是说这套流程的结果会成为该流程的新一次输入,从而形成一个闭环,此时的分析思维我们称之为循环/闭环思维。
常见的闭环思维如下:
- 业务流程闭环
- 生命周期闭环
- 产品功能使用闭环
- 市场推广策略闭环
本文列举常见的PDCA循环进行该思维的讲解。
2、PDCA循环
概念
PDCA循环法的概念是在管理学中被提出的,该方法的目的就是用于对当前的任务(事物)进行优化,达到精益求精的效果,简单的说就是按照一套标准的流程去不断完善当前的任务,得到最好的解决方案。
PDCA的组成如下:
- P(Plan)-计划
- D(D0)-执行
- C(Check)-检查
- A(Act)-处理
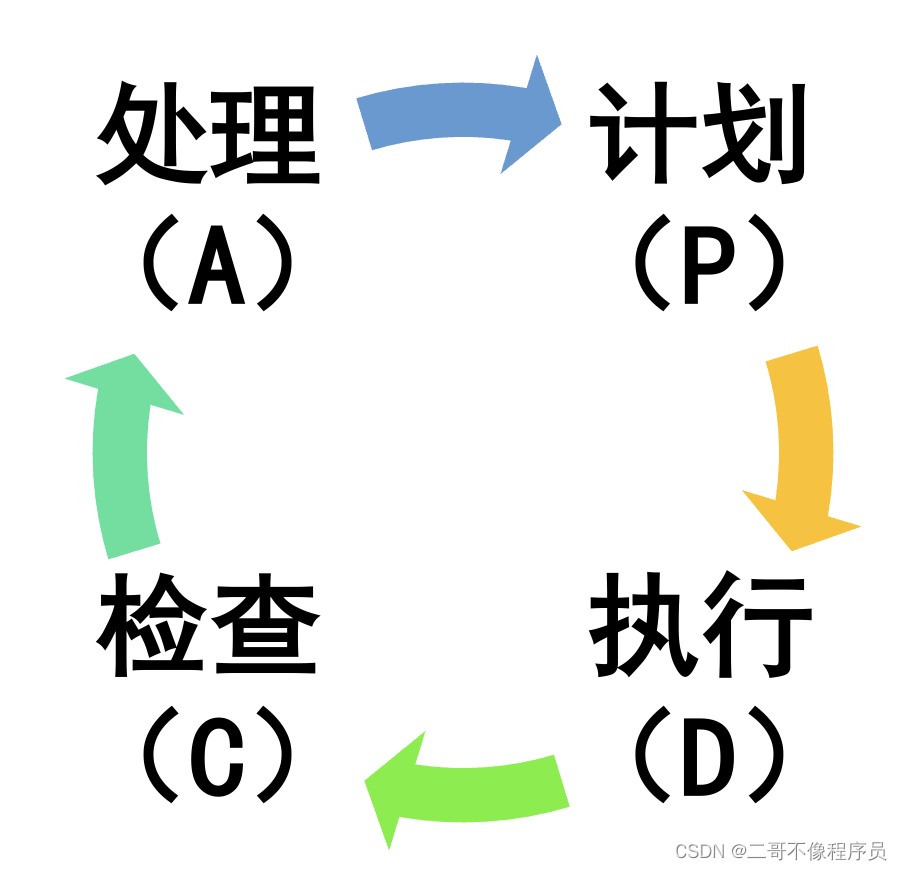
流程
PDCA的概念我们不难理解,那作为一个可以应用于很多场景的方法而言,我们应该如何去使用呢,下面通过8个步骤来了解一下一个闭环内的PDCA流程。
| 阶段 | 步骤 |
|---|---|
| P | 1、分析现状,找出问题 |
| 2、分析问题产生的各种原因 | |
| 3、找出主要的影响因素 | |
| 4、针对主要影响因素,制定计划 | |
| D | 5、执行计划 |
| C | 6、计划执行的结果展示 |
| A | 7、复盘总结,制定标准 |
| 8、问题总结,处理下一个问题 |
总结
上述的8个步骤不难理解,我们通过一次PDCA循环解决了一个重要问题,接下来的循环就是去解决该问题的分支或者第二重要的问题了,PDCA不会死板的要求我们一定按照某种顺序去解决,当问题有大有小时我们就先解决大问题,当问题有次序关系时,我们就按顺序进行解决即可。
除了PDCA循环之外,其他的闭环场景(产品功能闭环、用户生命周期闭环)等也适用于上述解决问题的思想。
3、举个例子
大家都参加过各大电商每年推出的618、双十一之类的活动,对于这类的运营活动推进我们就可以使用PDCA闭环进行分析,下面举一个简单的运营活动的PDCA闭环分析。
- 问题
某次运营活动,A公司想要实现1000W的GMV,应该如何设计活动?如何思考?
- 分析(P)
- 问题:如何实现1000W的GMV
- 拆分:公司现GMV来源可分为两部分人群——新用户/老用户
- 影响因素:新用户(品牌/产品曝光)|老用户(复购能力)
- 计划:新用户(打广告)|老用户(复购活动)
- 执行(D)
- 设计相应的广告及老用户的复购活动进行执行
- 检查(C)
- 活动进行一半,新用户完成40%,老用户完成60%
- 总结(A)
- 复盘:新用户点击广告的频率不高
- 调整:提高广告点击率(下一个PDCA)
- 总结:记录本次问题产生的原因(用作后续活动的经验)
上述的过程就是按照第2节中我们所提出的步骤进行拆分得到的结果,使用PDCA闭环,不难发现我们得到的条理非常清晰,但是也暴露出PDCA循环容易让我们产生惯性思维而缺少一些角度的思考的缺点。总体来说,模型就是一个基础,后续在不同的场景下我们可以进行适当的调整,最终形成属于自己的闭环思维即可。
