机器学习——06 集成学习

1 集成学习

1.1 简介

• 集成学习是机器学习里的一种重要思想；

  • 它的核心是把多个模型（称为弱学习器）组合起来，形成一个精度更高的模型；

  • 训练的时候，用训练集依次去训练这些弱学习器；在对未知样本做预测时，就靠这些弱学习器联合起来进行预测；

  • 从下图能更直观看到这个过程，训练集输入到多个基学习器（也就是弱学习器），基学习器处理后得到综合结果，最终输出预测结果；

    

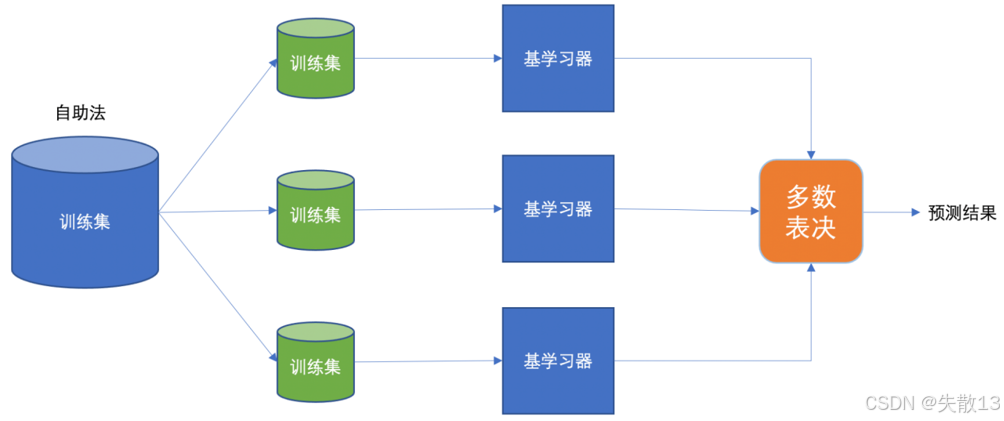
• 集成学习的优势：

  

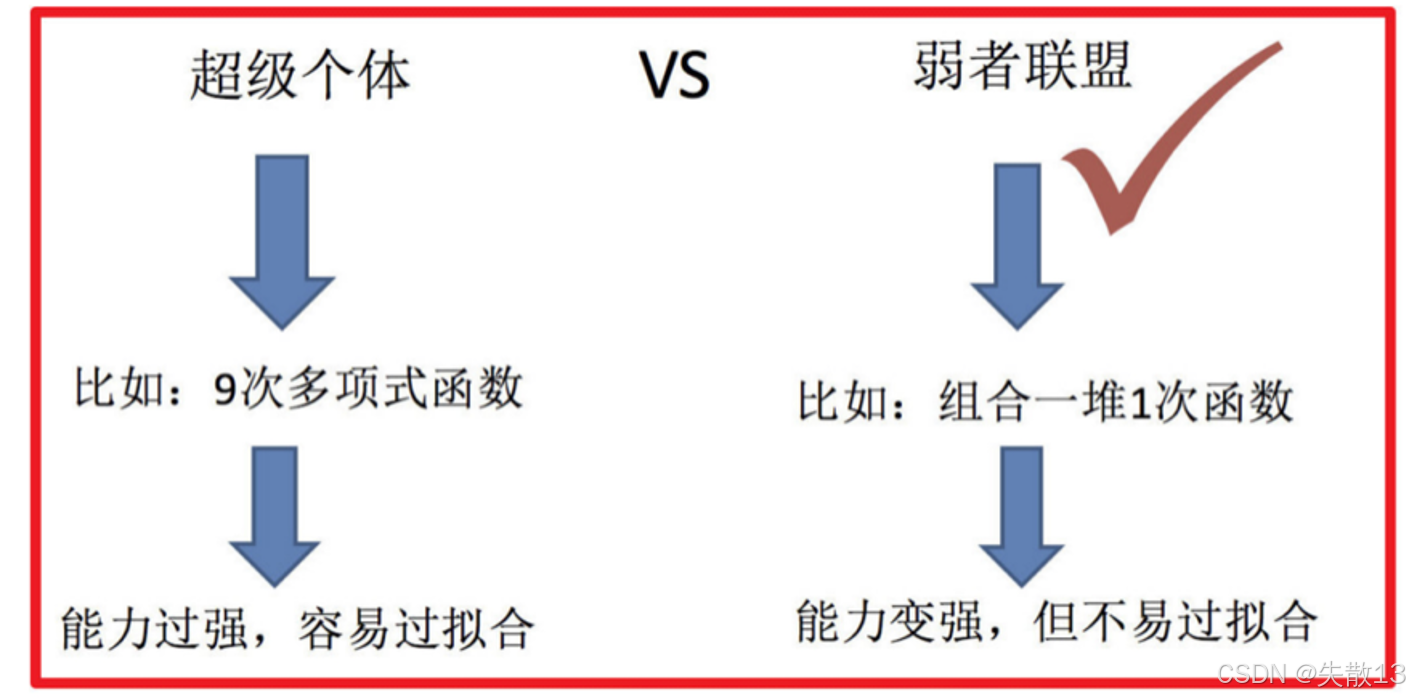
  • “超级个体”像9次多项式函数，能力很强但容易过拟合，也就是在训练数据上表现好，在新数据上可能表现差；
  • 而“弱者联盟”是组合一堆1次函数，集成后能力变强，还不容易过拟合，能更好地适应新数据；
  • 这表明集成学习通过组合多个弱学习器，在提升模型性能的同时，降低了过拟合的风险；

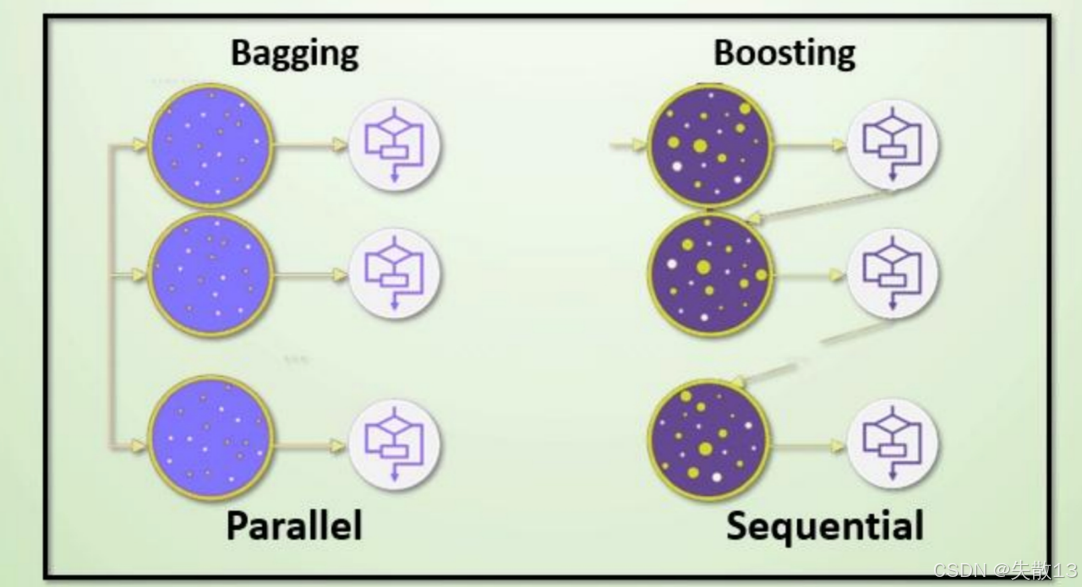
• 集成学习的分类：主要分为Bagging和Boosting两类

  

  • Bagging是并行（Parallel）的方式

    • 比如随机森林就属于Bagging方法；
    • 它通过对训练集进行有放回抽样，生成多个不同的子集，然后在每个子集上训练基学习器，最后通过投票或平均等方式综合结果；

  • Boosting是串行（Sequential）的方式

    • 像Adaboost、GBDT、XGBoost、LightGBM都属于Boosting方法；
    • 它的基学习器是依次训练的，后面的基学习器会根据前面基学习器的表现来调整样本的权重，重点关注前面分类错误的样本，逐步提升模型的性能。

1.2 Bagging 思想

• 流程：

  

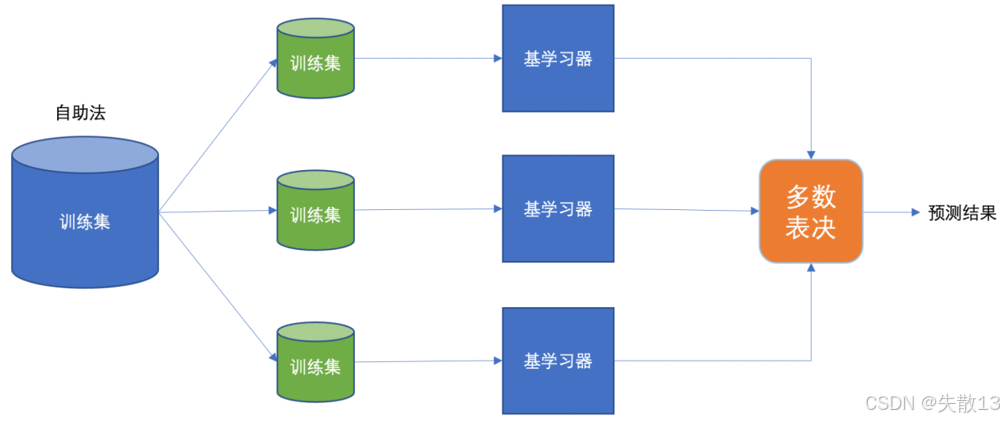
  • 首先通过自助法（也就是有放回的抽样，即booststrap抽样）从原始训练集中产生多个不同的训练集；
  • 然后用这些不同的训练集去训练不同的基学习器（弱学习器）；
  • 最后，通过平权投票或者多数表决的方式来决定预测结果；
  • 并且，这些弱学习器是可以并行训练的，因为它们之间相互独立，这样能提高训练的效率；

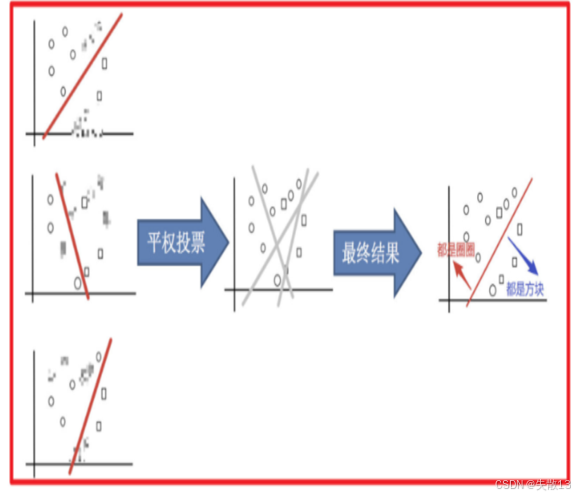
• 示例：以对圈和方块进行分类为例

  

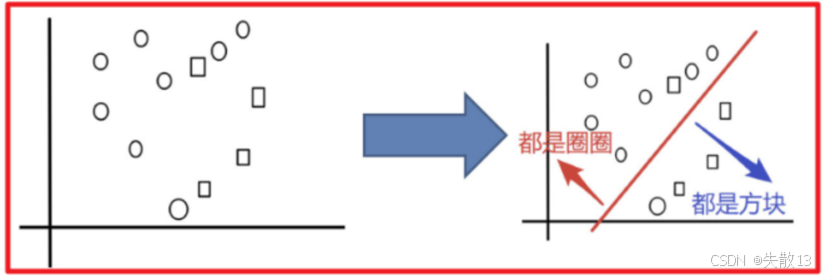
  • 采样不同数据集：首先对原始数据进行有放回的抽样，得到多个不同的数据集。这一步的目的是让每个基学习器都能在不同的数据分布上进行训练，增加模型的多样性；

    

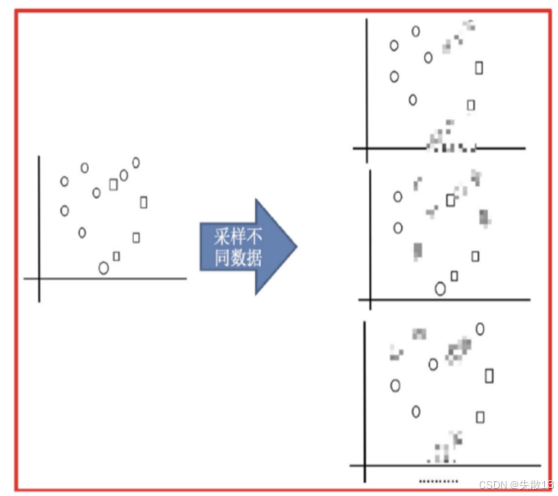
  • 训练分类器：用这些不同的数据集分别训练多个分类器。每个分类器在各自的数据集上学习，由于数据不同，每个分类器学到的模型也会有所差异；

    

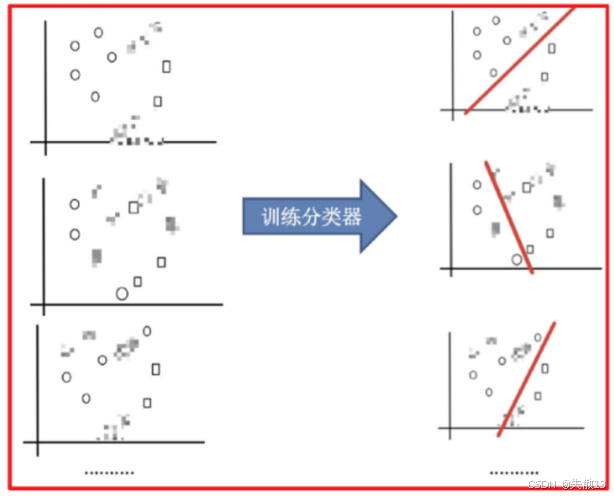
  • 平权投票，获取最终结果：最后，将这些分类器的预测结果进行平权投票。也就是每个分类器的投票权重是一样的，通过多数表决来确定最终的分类结果。这样可以综合多个分类器的优势，减少单个分类器可能出现的偏差，从而提高模型的准确性和泛化能力；

    

1.3 Boosting思想

• 流程：

  

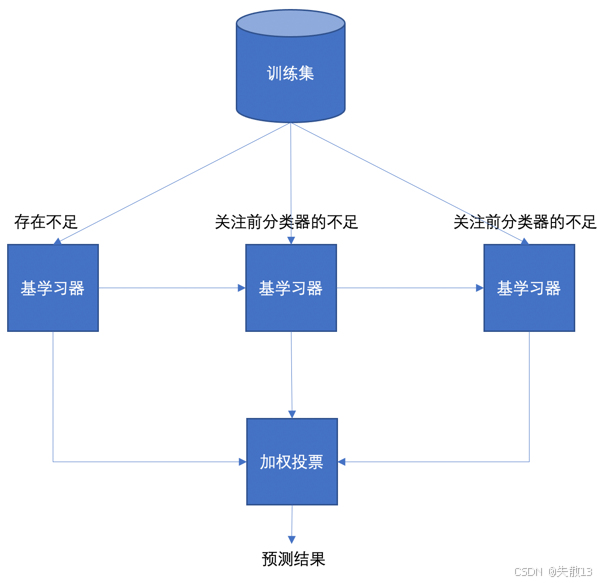
  • 首先有一个训练集，第一个基学习器存在不足，后面的基学习器会重点关注前一个基学习器的不足来进行训练；
  • 最后通过加权投票的方式得出预测结果；
  • Boosting采用的是串行的训练方式，因为后面的基学习器依赖于前面基学习器的结果；

• 例：

  

  • 滚球兽逐步进化为更强大的战斗暴龙兽，就像Boosting中随着弱学习器的不断加入，整体模型的能力从弱到强逐步提升；
  • 每新加入一个弱学习器，都会针对之前模型的不足进行改进，从而使整体能力得到提升；

• Boosting的代表算法有Adaboost、GBDT、XGBoost、LightGBM等。

1.4 Bagging VS Boosting

• 数据采样：

  • Bagging是对数据进行有放回的采样来训练不同的基学习器；
  • 而Boosting使用全部样本，但是会根据前一轮学习结果调整数据的重要性，也就是对之前分类错误的样本增加权重，让后续的基学习器更关注这些样本；

• 投票方式：

  • Bagging中所有学习器是平权投票，每个基学习器的权重相同；
  • Boosting则是对学习器进行加权投票，通常表现好的基学习器会有更高的权重；

• 学习顺序：

  • Bagging是并行的，每个学习器之间没有依赖关系，可以同时训练；
  • Boosting是串行的，学习有先后顺序，后面的学习器依赖于前面学习器的结果。

2 随机森林算法

2.1 概述

• 随机森林是基于Bagging思想实现的一种集成学习算法，它采用决策树模型作为每一个弱学习器

  • 训练过程：首先通过有放回的方式产生训练样本（自助法），然后在每个训练样本上随机挑选n个特征（n小于总特征数量）来训练基学习器（决策树）

  • 预测过程：通过平权投票、多数表决的方式输出预测结果；

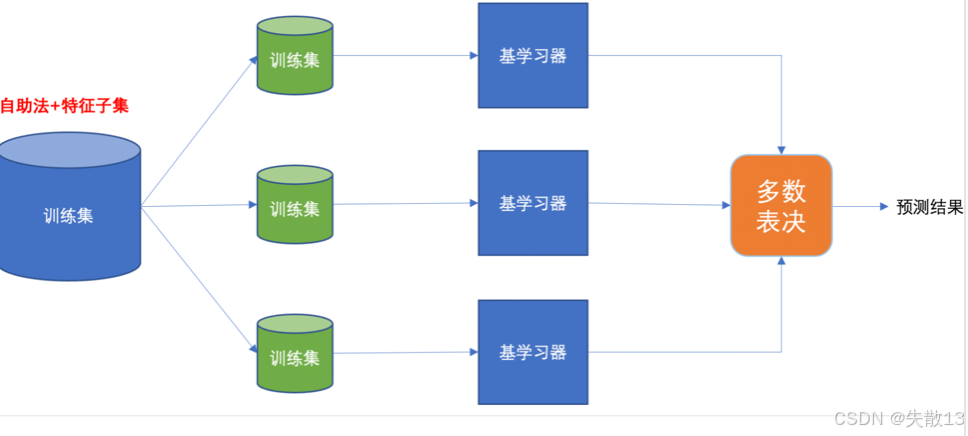
  • 如下图，原始训练集通过自助法和特征子集的方式生成多个训练集，每个训练集训练一个基学习器，最后通过多数表决得到预测结果

    

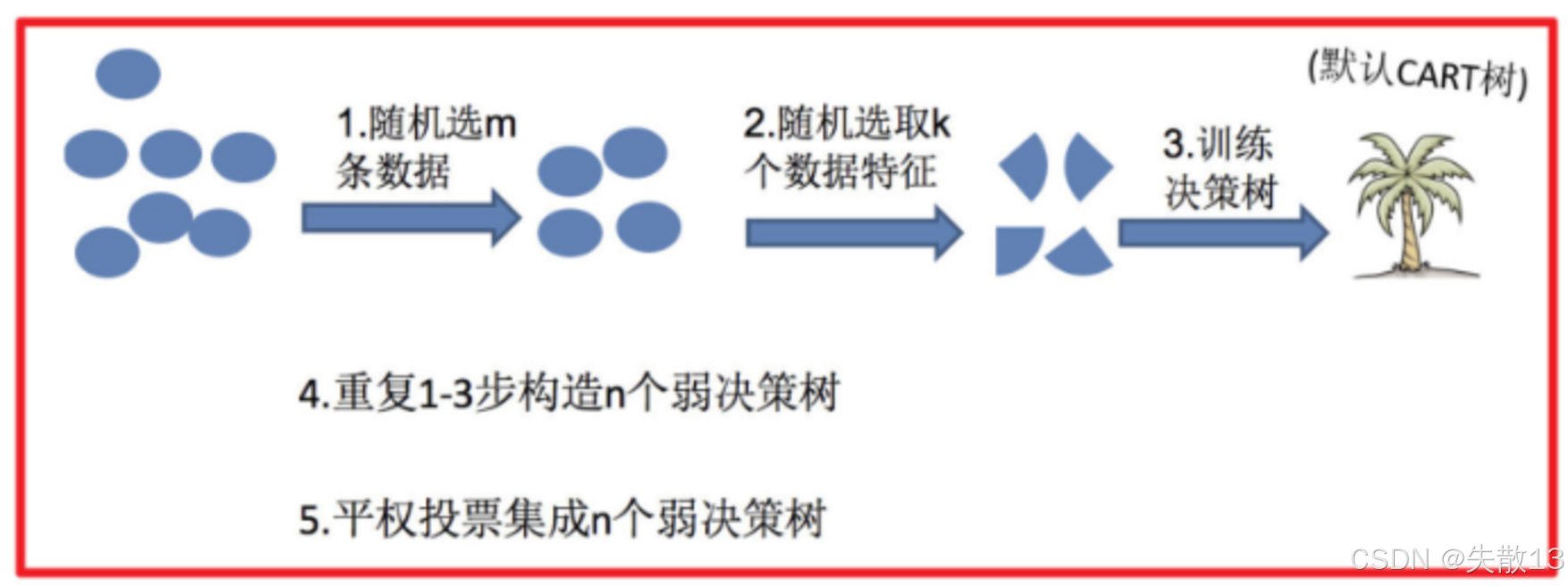
• 随机森林的步骤

  1. 随机选m条数据
  2. 随机选取k个数据特征
  3. 训练决策树（默认是CART树）
  4. 重复1-3步构造n个弱决策树
  5. 平权投票集成n个弱决策树，得到最终的预测结果

  

• 随机森林的关键问题

  • **为什么要随机抽样训练集？**如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也会完全一样，这样就失去了集成学习的意义，无法通过多个基学习器的组合来提升模型的性能和泛化能力；

  • **为什么要有放回地抽样？**如果不是有放回的抽样，那么每棵树的训练样本都是不同的，没有交集，这样每棵树都是“有偏的”，训练出来的树差异很大。而随机森林最后分类取决于多棵树的投票表决，有放回地抽样可以让弱学习器的训练样本既有交集也有差异数据，更容易发挥投票表决的效果，提高模型的准确性和稳定性。

2.2 API

• sklearn.ensemble.RandomForestClassifier()的一些主要参数：

  • n_estimators：决策树的数量，默认是10

  • Criterion：用于衡量分裂质量的函数，可选entropy（熵）或者gini（基尼系数），默认是gini

  • max_depth：指定树的最大深度，默认是None，表示树会尽可能地生长

  • max_features：决策树构建时使用的最大特征数量。参数值有：

    • “auto”（默认，等于sqrt(n_features)）
    • “sqrt”（和"auto"一样）
    • “log2”（等于log2(n_features)）
    • None（等于n_features）

  • bootstrap：是否采用有放回抽样，默认是True。如果为False，将会使用全部训练样本

  • min_samples_split：结点分裂所需的最小样本数，默认是2。如果节点样本数少于这个值，则不会再进行划分。样本量不大时不需要设置，样本量非常大时推荐增大这个值

  • min_samples_leaf：叶子节点的最小样本数，默认是1。如果某叶子节点数目小于这个值，则会和兄弟节点一起被剪枝。较小的叶子节点样本数量使模型更容易捕捉训练数据中的噪声

  • min_impurity_split：节点划分的最小不纯度，默认是1e-7。如果某节点的不纯度（基尼系数、均方差）小于这个阈值，则该节点不再生成子节点，变为叶子节点。一般不推荐改动默认值

2.3 案例

• 导包：

  # 0.导包
  import pandas as pd
  from sklearn.model_selection import train_test_split
  from sklearn.tree import DecisionTreeClassifier
  from sklearn.ensemble import RandomForestClassifier
  from sklearn.model_selection import GridSearchCV
  

• 读取数据：

  # 1.读取数据
  data =pd.read_csv('data/titanic/train.csv')
  print(data.head())
  print(data.info())
  

• 数据处理：

  # 2.数据处理
  x = data[['Pclass','Sex','Age']].copy()
  y = data['Survived'].copy()
  print(x.head(10))
  x['Age'].fillna(x['Age'].mean(),inplace = True)
  print(x.head(10))
  x=pd.get_dummies(x) # 独热编码
  print(x.head(10))x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2)
  

• 模型训练：

  # 3.模型训练
  # 3.1 决策树
  # 导入决策树分类器并实例化一个决策树模型（使用默认参数）
  tree = DecisionTreeClassifier()
  # 使用训练数据集（x_train为特征数据，y_train为标签数据）训练决策树模型
  tree.fit(x_train, y_train)# 3.2 随机森林
  # 导入随机森林分类器并实例化一个随机森林模型（使用默认参数）
  rf = RandomForestClassifier()
  # 使用训练数据集训练随机森林模型
  rf.fit(x_train, y_train)# 3.3 网格搜索交叉验证
  # 定义需要搜索的超参数组合：
  # n_estimators：随机森林中决策树的数量，候选值为10和20
  # max_depth：决策树的最大深度，候选值为2、3、4、5
  params = {'n_estimators': [10, 20], 'max_depth': [2, 3, 4, 5]}# 创建网格搜索对象：
  # estimator=rf：指定要优化的基础模型为随机森林
  # param_grid=params：指定超参数搜索范围
  # cv=3：采用3折交叉验证，将训练集分成3份，轮流用2份训练1份验证
  model = GridSearchCV(estimator=rf, param_grid=params, cv=3)# 执行网格搜索，找到最佳超参数组合
  model.fit(x_train, y_train)# 输出最佳超参数对应的模型（包含最优参数配置）
  print(model.best_estimator_)# 根据网格搜索得到的最佳超参数（假设是max_depth=4, n_estimators=10）
  # 实例化一个新的随机森林模型
  rfs = RandomForestClassifier(max_depth=4, n_estimators=10)
  # 使用最佳超参数配置的模型重新训练
  rfs.fit(x_train, y_train)
  

  

• 模型评估：

  # 4.模型评估
  # 4.1 决策树
  print(tree.score(x_test,y_test))
  # 4.2 随机森林
  print(rf.score(x_test,y_test))
  # 4.3 网格搜索交叉验证
  print(rfs.score(x_test,y_test))
  

  

3 Adaboost算法

3.1 概述

• Adaboost（Adaptive Boosting，自适应提升）是基于Boosting思想实现的一种集成学习算法；

  • 它的核心思想是通过逐步提高那些被前一步分类错误的样本的权重，来训练一个强分类器；
  • 也就是说，每一轮训练都会更加关注上一轮分类错误的样本，使得后续的弱学习器能够针对性地对这些样本进行学习，从而逐步提升整体模型的性能；

• Adaboost算法的步骤

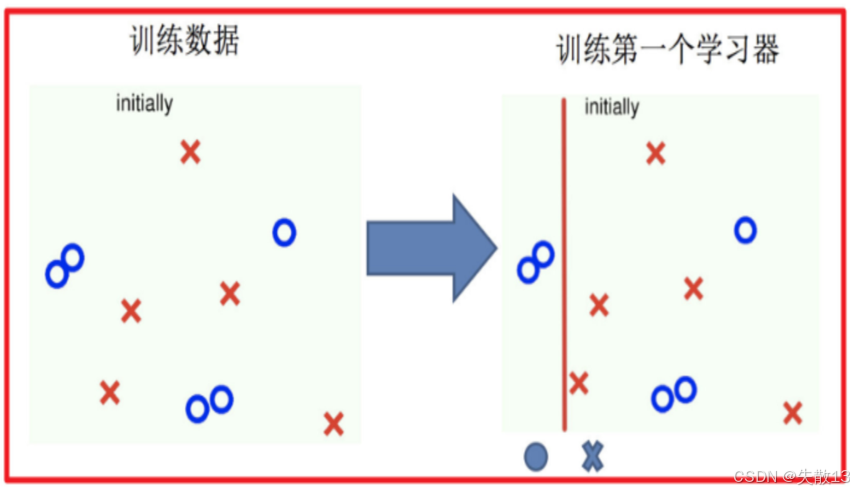
  1. 训练第一个学习器：

     • 首先使用初始的训练数据训练第一个弱学习器；
     • 如下图：初始的训练数据分布较为均匀，经过训练得到第一个学习器（用红色的线表示分类边界）；

     

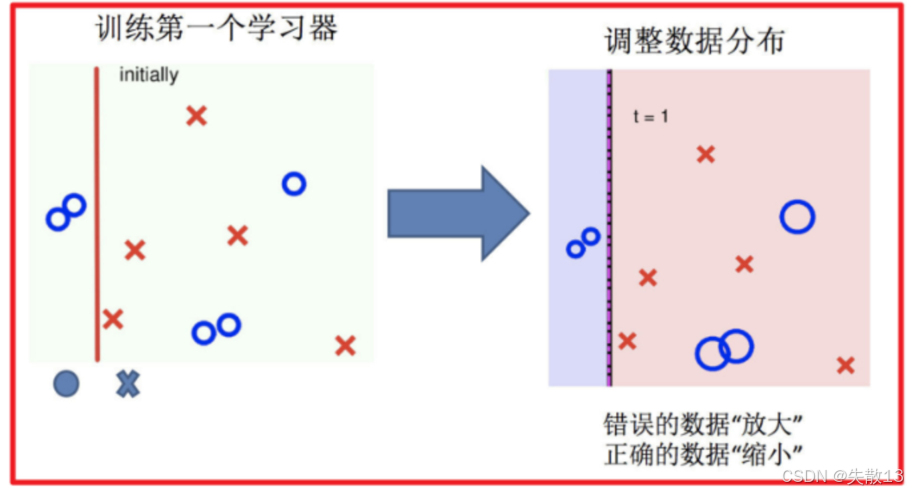
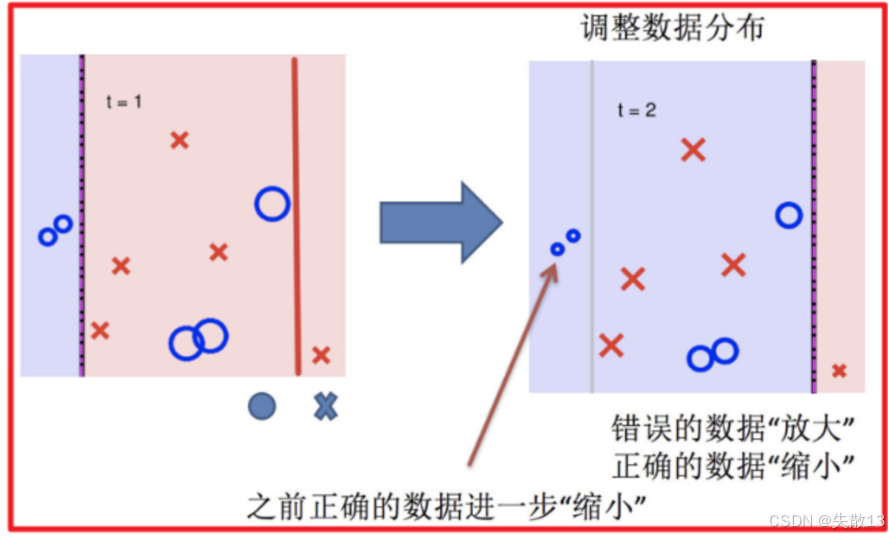
  2. 调整数据分布：

     • 根据第一个学习器的分类结果，调整训练数据的分布；
     • 对于被第一个学习器分类错误的样本（图中被错误分类的点），增加它们的权重；
     • 对于分类正确的样本，降低它们的权重；
     • 这样，在后续的训练中，模型会更加关注这些被错误分类的样本；
     • 如下图，错误的数据被“放大”（权重增加），正确的数据被“缩小”（权重降低）；

     

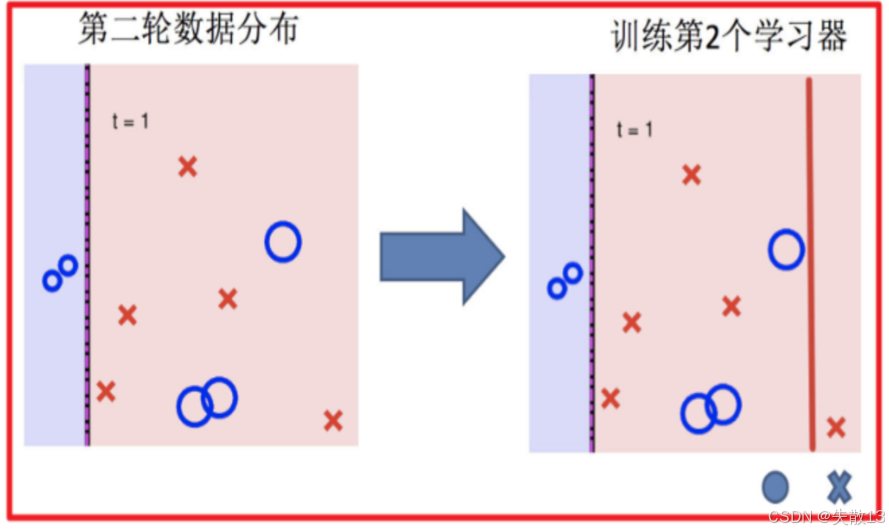
  3. 训练第二个学习器：

     • 使用调整后的数据分布训练第二个弱学习器；
     • 如下图，第二轮的数据分布已经发生了变化，错误样本的权重增加，正确样本的权重降低；
     • 第二个学习器（用红色的线表示分类边界）会在这种新的数据分布下进行训练，重点学习那些被第一个学习器分类错误的样本；

     

  4. 再次调整数据分布：

     • 根据第二个学习器的分类结果，再次调整数据分布；
     • 同样地，增加被第二个学习器分类错误的样本的权重，降低分类正确的样本的权重；
     • 如下图，之前被正确分类的数据进一步被“缩小”（权重进一步降低），错误的数据继续被“放大”（权重继续增加）；

     

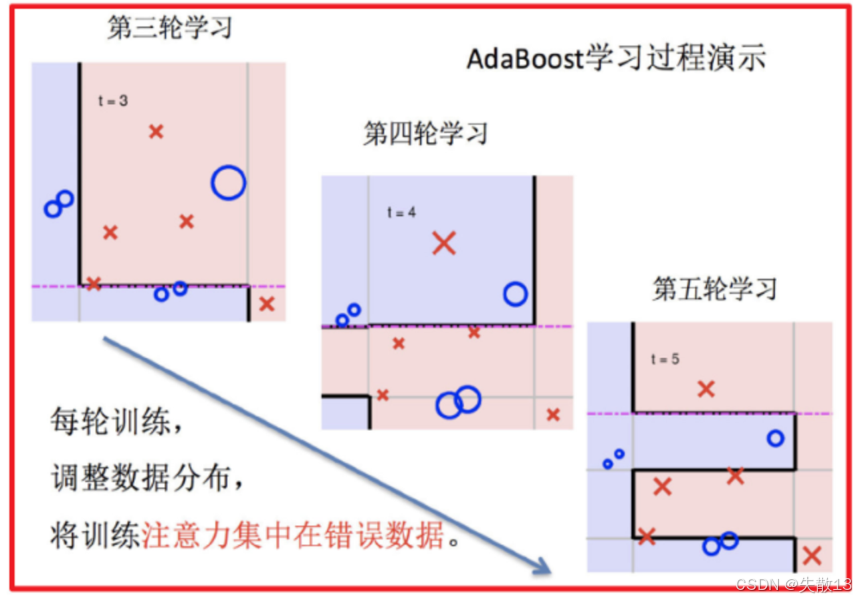
  5. 依次训练学习器，调整数据分布：

     • 重复步骤3和步骤4，依次训练更多的弱学习器，并不断调整数据分布；

     • 每一轮训练都会让新的弱学习器重点关注之前被分类错误的样本；

     • 从下图的左侧可以看到，经过多轮训练（第三轮、第四轮、第五轮等），每轮训练都会调整数据分布，将训练注意力集中在错误数据上；

       

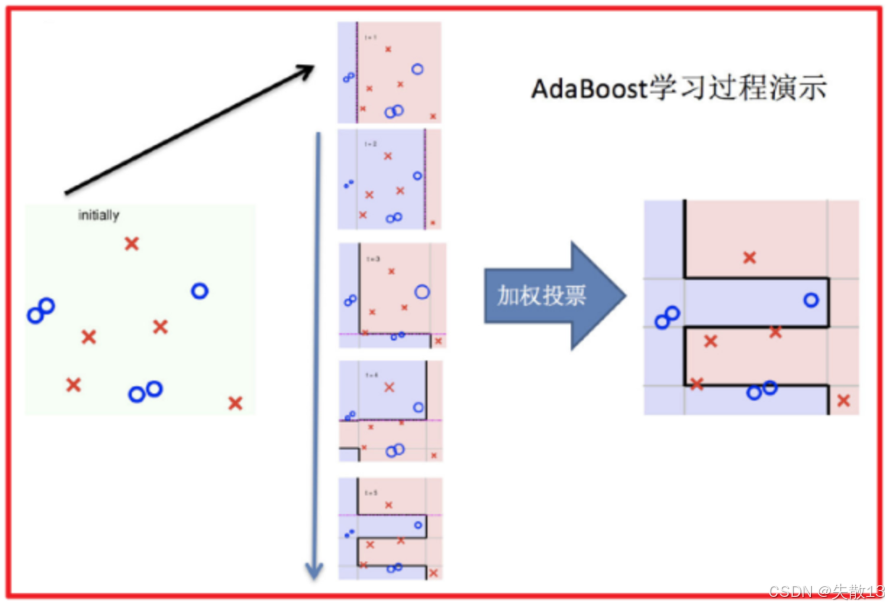
  6. 整体过程实现：

     • 将所有训练好的弱学习器通过加权投票的方式组合成一个强分类器；
     • 每个弱学习器的权重根据其在训练过程中的表现来确定，表现越好的弱学习器权重越高；
     • 如下图，初始数据经过多轮训练得到多个弱学习器，最后通过加权投票的方式得到最终的分类结果，从而实现对样本的准确分类；

     

• 特点：

  • Adaboost算法通过不断调整样本权重，使得后续的弱学习器能够针对性地学习之前被错误分类的样本，从而逐步提升模型的性能；
  • 这种方法充分利用了多个弱学习器的优势，通过加权组合形成一个强分类器，具有较好的准确性和泛化能力；
  • 同时，Adaboost算法不需要预先知道弱学习器的错误率上限，并且计算简单，容易实现。

3.2 算法推导

1. 初始化训练数据权重：

   • 首先，将训练数据集中每个样本的权重初始化为相等的值。例如，如果有100个样本，每个样本的初始权重为1/100；
   • 然后，使用这些初始权重训练第一个弱学习器。在训练过程中，根据预测结果找到一个错误率最小的分裂点，以此来计算和更新样本权重以及模型权重；

2. 根据新权重训练后续学习器：

   • 基于上一轮训练得到的新样本权重，训练第二个弱学习器。同样地，根据预测结果找到错误率最小的分裂点，计算并更新样本权重和模型权重；
   • 重复这个过程，迭代训练后续的弱学习器。每一轮训练都在前一个学习器的基础上，根据新的样本权重来训练当前的学习器，直到训练出m个弱学习器；

3. 集成弱学习器进行预测：

   • 最后，将这m个弱学习器通过加权投票的方式集成起来，得到最终的预测模型；

   • 集成预测公式为：
     $$H(x)=sign(\sum _{i=1}^m{\alpha }_i{h}_i(x))$$

     • 其中${\alpha }_i$是每个弱学习器的权重。如果输出结果大于0，则将样本归为正类；如果小于0，则归为负类；

• 关键公式：

  • 模型权重计算公式：
    $${\alpha }_t=\frac{1}{2}\ln \left(\frac{1-{ϵ}_t}{{ϵ}_t}\right)$$

    • 其中，${\alpha }_t$是第t个弱学习器的权重，${ϵ}_t$是第t个弱学习器的错误率；
    • 这个公式表明，错误率越低的弱学习器，其权重越高，在最终的集成模型中发挥的作用越大；

  • 样本权重计算公式：
    $$D_{t+1}(x)=\frac{D_t(x)}{Z_t}\times \{\begin{array}{ll}{e}^{-{\alpha }_t},& \text{如果预测值等于真实值}\\ e^{{\alpha }_t},& \text{如果预测值不等于真实值}\end{array}$$

    • 其中，$D_t(x)$是第t轮训练中样本x的权重，$Z_t$是归一化因子（所有样本权重的总和），${\alpha }_t$是第t个弱学习器的权重；
    • 这个公式的作用是调整样本的权重，使得被错误分类的样本在后续的训练中具有更高的权重，从而让后续的弱学习器更加关注这些样本。

3.3 分类器构建过程

• 已知训练数据（包含10个样本，特征为x，标签为y），假设弱分类器由x产生，要求使用Adaboost算法学习一个强分类器，使得该分类器在训练数据集上的分类误差率最低；

  

3.3.1 构建第1个弱分类器

1. 初始化样本权重：将10个样本的权重初始化为相等的值，每个样本的权重为0.1；

   

2. 寻找最优分裂点：

   • 对特征值x进行排序，确定可能的分裂点为0.5、1.5、2.5、3.5、4.5、5.5、6.5、7.5、8.5；

   • 分别计算以每个分裂点进行分类时的错误率：

     对于每个分裂点，将样本分为两部分（小于分裂点和大于分裂点），并预测每部分的类别。然后比较预测类别与实际类别 $ y $，统计分类错误的样本数量

     • 以0.5为分裂点时，有5个样本分类错误

       小于 $ 0.5 $ 的样本：$ x = 0 $，预测类别为 $ 1 $（实际类别 $ y = 1 $，正确）

       大于 $ 0.5 $ 的样本：$ x = 1, 2, 3, 4, 5, 6, 7, 8, 9 $，预测类别为 $ -1 $

       • 实际类别 $ y $ 为 $ -1 $ 的样本：$ x = 3, 4, 5, 9 $（正确）
       • 实际类别 $ y $ 为 $ 1 $ 的样本：$ x = 1, 2, 6, 7, 8 $（错误）

       错误样本数量：$ 5 $（$ x = 1, 2, 6, 7, 8 $）

       错误率：$ 5/10 = 0.5 $

     • 以1.5为分裂点时，有4个样本分类错误

       小于 $ 1.5 $ 的样本：$ x = 0, 1 $，预测类别为 $ 1 $（实际类别 $ y = 1 $，正确）

       大于 $ 1.5 $ 的样本：$ x = 2, 3, 4, 5, 6, 7, 8, 9 $，预测类别为 $ -1 $

       • 实际类别 $ y $ 为 $ -1 $ 的样本：$ x = 3, 4, 5, 9 $（正确）
       • 实际类别 $ y $ 为 $ 1 $ 的样本：$ x = 2, 6, 7, 8 $（错误）

       错误样本数量：$ 4 $（$ x = 2, 6, 7, 8 $）

       错误率：$ 4/10 = 0.4 $

     • 以2.5为分裂点时，有3个样本分类错误

       小于 $ 2.5 $ 的样本：$ x = 0, 1, 2 $，预测类别为 $ 1 $（实际类别 $ y = 1 $，正确）

       大于 $ 2.5 $ 的样本：$ x = 3, 4, 5, 6, 7, 8, 9 $，预测类别为 $ -1 $

       • 实际类别 $ y $ 为 $ -1 $ 的样本：$ x = 3, 4, 5, 9 $（正确）
       • 实际类别 $ y $ 为 $ 1 $ 的样本：$ x = 6, 7, 8 $（错误）

       错误样本数量：$ 3 $（$ x = 6, 7, 8 $）

       错误率：$ 3/10 = 0.3 $

     • 以3.5为分裂点时，有4个样本分类错误

     • 以4.5为分裂点时，有5个样本分类错误

     • 以5.5为分裂点时，有4个样本分类错误

     • 以6.5为分裂点时，有5个样本分类错误

     • 以7.5为分裂点时，有4个样本分类错误

     • 以8.5为分裂点时，有3个样本分类错误

   • 最终选择错误率最低的分裂点2.5，此时基学习器的错误率为3/10 = 0.3

3. 计算模型权重：根据公式${\alpha }_t=\frac{1}{2}\ln \left(\frac{1-{ϵ}_t}{{ϵ}_t}\right)$，其中${ϵ}_t$是第t个弱学习器的错误率，计算得到第一个弱学习器的权重${\alpha }_1=\frac{1}{2}\ln \left(\frac{1-0.3}{0.3}\right)\approx 0.4236$；

4. 更新样本权重：

   • 分类正确的样本（样本1、2、3、4、5、6、10）的权重调整系数为$e^{-{\alpha }_1}\approx 0.6547$
   • 分类错误的样本（样本7、8、9）的权重调整系数为$e^{{\alpha }_1}\approx 1.5275$
   • 计算归一化因子$Z_1=0.06547\times 7+0.15275\times 3\approx 0.9165$
   • 分类正确样本的最终权重为$0.06547/0.9165\approx 0.07143$
   • 分类错误样本的最终权重为$0.15275/0.9165\approx 0.1667$

   

3.3.2 构建第2个弱分类器

1. 寻找最优分裂点：

   • 同样对特征值x进行排序，确定分裂点为0.5、1.5、2.5、3.5、4.5、5.5、6.5、7.5、8.5

   • 分别计算以每个分裂点进行分类时的错误率（根据更新后的样本权重）：

     • 以0.5为分裂点时，错误率为$0.07143\times 5=0.35715$

       分裂规则：小于 0.5 的样本（$ x = 0 $）预测为 $ 1 $，大于0.5的样本（$ x = 1, 2, 3, 4, 5, 6, 7, 8, 9 $）预测为 $ -1 $

       分类错误的样本：实际类别 $ y = 1 $ 的样本（$ x = 1, 2, 6, 7, 8 $）被错误预测为 $ -1 $

       错误率计算：每个错误样本的权重为 $ 0.07143 $，错误率 = $ 0.07143 \times 5 = 0.35715 $

     • 以1.5为分裂点时，错误率为$0.07143\times 1+0.16667\times 3=0.57144$

       分裂规则：小于 1.5 的样本（$ x = 0, 1 $）预测为 $ 1 $，大于1.5的样本（$ x = 2, 3, 4, 5, 6, 7, 8, 9 $）预测为 $ -1 $

       分类错误的样本：实际类别 $ y = 1 $ 的样本（$ x = 2, 6, 7, 8 $）被错误预测为 $ -1 $，实际类别 $ y = -1 $ 的样本（$ x = 3 $）被错误预测为 $ 1 $

       错误率计算：样本 $ x = 3 $ 的权重为 $ 0.07143 $，样本 $ x = 2, 6, 7, 8 $ 的权重为 $ 0.16667 $，错误率 = $ 0.07143 \times 1 + 0.16667 \times 3 = 0.57144 $

     • 以2.5为分裂点时，错误率为$0.16667\times 3=0.57144$

     • 以8.5为分裂点时，错误率为$0.07143\times 3=0.21429$

   • 最终选择错误率最低的分裂点8.5，此时基学习器的错误率为0.21429

2. 计算模型权重：根据公式计算得到第二个弱学习器的权重${\alpha }_2=\frac{1}{2}\ln \left(\frac{1-0.21429}{0.21429}\right)\approx 0.64963$

3. 更新样本权重：

   • 分类正确的样本（样本1、2、3、7、8、9、10）的权重调整系数为$e^{-{\alpha }_2}\approx 0.5222$
   • 分类错误的样本（样本4、5、6）的权重调整系数为$e^{{\alpha }_2}\approx 1.9148$
   • 计算归一化因子$Z_2=0.0373\times 4+0.087\times 3+0.1368\times 3\approx 0.8206$
   • 分类正确样本的最终权重分别为0.0455和0.1060
   • 分类错误样本的最终权重为0.1667

   

3.3.3 构建第3个弱分类器

1. 寻找最优分裂点：经过类似的计算过程，选择分裂点5.5，此时基学习器的错误率为0.1820。
2. 计算模型权重：根据公式计算得到第三个弱学习器的权重${\alpha }_3\approx 0.7514$。

3.3.4 最终强学习器

• 将这三个弱学习器通过加权投票的方式集成起来，得到最终的强分类器：
  $$H(x)=\text{sign}\left(0.4236\times h_1(x)+0.64963\times h_2(x)+0.7515\times h_3(x)\right)$$

  • 其中，$h_1(x)$、$h_2(x)$、$h_3(x)$分别是三个弱学习器的预测结果；

• 如果$H(x)$的值大于0，则将样本归为正类；如果小于0，则归为负类；

• 例如，当$x=3$时，代入公式计算得到$H(3)\approx -0.52537<0$，所以样本被归为负类。

3.4 案例：葡萄酒分类

• 导包：

  import pandas as pd
  from sklearn.preprocessing import LabelEncoder
  from sklearn.ensemble import AdaBoostClassifier
  from sklearn.model_selection import train_test_split
  

• 数据处理：

  # 读取数据
  data = pd.read_csv('data/wine0501.csv')
  print(data.info())
  # 数据筛选：从数据集中排除'Class label'为1的样本，只保留标签不为1的样本
  data = data[data['Class label'] != 1]
  x = data[['Alcohol', 'Hue']].copy()
  y = data['Class label'].copy()
  print(y)# 初始化标签编码器，用于将类别标签转换为模型可处理的整数
  pre = LabelEncoder()
  # 对标签y进行编码：将原始类别标签（如2、3等）转换为0、1等整数形式
  y = pre.fit_transform(y)
  # 打印编码后的标签数据，确认编码结果是否正确
  print(y)x_train, x_test, y_train, y_test = train_test_split(x, y)
  

  

• 模型训练：

  # 模型训练
  ada = AdaBoostClassifier()
  ada.fit(x_train,y_train)
  

• 模型评估：

  # 模型评估
  print(ada.score(x_test,y_test))
  

4 GBDT算法

4.1 提升树

• 核心思想：
  • 提升树（Boosting Decision Tree）通过拟合残差的思想来进行提升。残差是指真实值与预测值之间的差异，即残差 = 真实值 - 预测值；
  • 通过不断地拟合残差，提升树能够逐步减少模型的预测误差，从而提高模型的性能；
• 生活中的例子：
  • 以预测某人的年龄为例，假设真实年龄是100岁
  • 第一次预测：预测结果为80岁，残差为100 - 80 = 20岁
  • 第二次预测：以第一次的残差20岁作为目标值，预测结果为16岁，残差为20 - 16 = 4岁
  • 第三次预测：以第二次的残差4岁作为目标值，预测结果为3.2岁，残差为4 - 3.2 = 0.8岁
  • 将三次预测的结果串联起来：80 + 16 + 3.2 = 99.2岁，与真实年龄100岁非常接近
  • 这个例子表明，通过拟合残差，可以将多个弱学习器组合成一个强学习器，这就是提升树的最朴素思想

4.2 梯度提升树

• 核心思想：梯度提升树（Gradient Boosting Decision Tree，GBDT）不再直接拟合残差，而是利用梯度下降的近似方法，利用损失函数的负梯度作为提升树算法中的残差近似值；
• 数学推导：
  • 假设前一轮迭代得到的强学习器是$ f_{t-1}(x) $；
  • 损失函数为平方损失：$ L(y, f_{t-1}(x)) $；
  • 本轮迭代的目标是找到一个弱学习器$ h_t(x) $，使得本轮的损失最小化：$ L(y, f_t(x)) = L(y, f_{t-1}(x)) + l = (y - f_{t-1}(x) - h_t(x))^2 $；
  • 要拟合的负梯度为：$ -\left[ \frac{\partial L(y, f(x_i))}{\partial f(x_i)} \right] = y_i - f(x_i) $；
  • 对于GBDT来说，拟合的负梯度就是残差。如果GBDT用于分类问题，损失函数变为对数损失（logloss），此时拟合的目标值就是该损失函数的负梯度值。

4.3 案例

• 已知数据：有一个包含10个样本的数据集，每个样本有一个特征 $ x $ 和一个目标值（真实值）；

  

4.3.1 初始化弱学习器（CART树）

• 找到一个预测值，使得第一个弱学习器的平方误差最小。即：求损失函数对 $f(x_i)$ 的导数，并令导数为0；

• 平方损失函数：
  $$L(y,f(x))=\frac{1}{2}\sum _{i=1}^n(y_i-f(x_i){)}^2$$

  • 其中，$ y_i $ 是真实值，$ f(x_i) $ 是预测值；

• 为了找到使平方损失最小的预测值 $ f(x_i) $，对损失函数关于 $ f(x_i) $ 求导，并令导数为0：
  $$\begin{gathered} \frac{\partial L(y,f(x))}{\partial f(x_i)}=\sum _{i=1}^n(y_i-f(x_i))\times (-1)=0 \\ 化简得：\sum _{i=1}^n(y_i-f(x_i))=0 \\ 进一步整理得：\sum _{i=1}^n{y}_i=\sum _{i=1}^{n}f(x_i) \end{gathered}$$

• 由于所有样本的预测值 $ f(x_i) $ 相同（初始化时），设为 $ \bar{y} $，则：
  $$\begin{gathered} \sum _{i=1}^n{y}_i=n\bar{y} \\ 解得：\bar{y}=\frac{{\sum }_{i=1}^n{y}_i}{n} \end{gathered}$$

• 通过上述推导可知，使平方损失最小的预测值 $ f(x_i) $ 是所有样本真实值的均值。因此，初始化时所有样本的预测值均为真实值的均值;

• 计算均值：
  $$\text{均值}=\frac{5.56+5.70+5.91+6.40+6.80+7.05+8.90+8.70+9.00+9.05}{10}=7.31$$

• 初始化预测值：所有样本的预测值均为7.31；

  

4.3.2 构建第1个弱学习器

• 计算负梯度（残差）：

  • 公式：其中，$ y_i $ 是真实值，$ f(x_i) $ 是预测值
    $$\text{负梯度}=y_i-f(x_i)$$

  • 计算结果如下：

    

• 寻找最优切分点：

  • 尝试不同的切分点（1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5），计算每个切分点的平方损失

  • 平方损失计算公式：
    $$\text{平方损失}=\sum (y_i-f(x_i){)}^2$$

  • 计算结果如下：

    

    以切分点 1.5 为例：

    • 小于 1.5 的样本（$ x = 1 $）：负梯度为 -1.75，拟合值为 -1.75

    • 大于 1.5 的样本（$ x = 2, 3, 4, 5, 6, 7, 8, 9, 10 $）：负梯度分别为 -1.61, -1.40, -0.91, -0.51, -0.26, 1.59, 1.39, 1.69, 1.74

    • 拟合值为这些负梯度的均值：
      $$\text{均值}=\frac{-1.61-1.40-0.91-0.51-0.26+1.59+1.39+1.69+1.74}{9}\approx 0.19$$

    • 平方损失计算：
      $$\text{平方损失}=(-1.75-(-1.75){)}^2+\sum _{i=2}^{10}(y_i-0.19{)}^2\approx 15.72$$

    以切分点 2.5 为例：

    • 小于 2.5 的样本（$ x = 1, 2 $）：负梯度分别为 -1.75, -1.61，拟合值为 -1.68

    • 大于 2.5 的样本（$ x = 3, 4, 5, 6, 7, 8, 9, 10 $）：负梯度分别为 -1.40, -0.91, -0.51, -0.26, 1.59, 1.39, 1.69, 1.74

    • 拟合值为这些负梯度的均值：
      $$\text{均值}=\frac{-1.40-0.91-0.51-0.26+1.59+1.39+1.69+1.74}{8}\approx 0.47$$

    • 平方损失计算：
      $$\text{平方损失}=(-1.75-(-1.68){)}^2+(-1.61-(-1.68){)}^2+\sum _{i=3}^{10}(y_i-0.47{)}^2\approx 12.08$$

  • 选择平方损失最小的切分点6.5，此时平方损失为1.93；

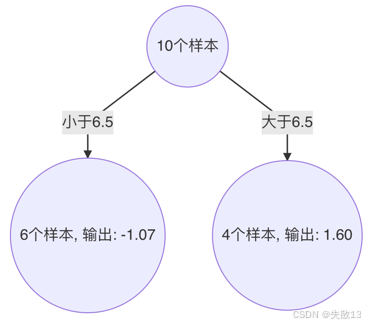
• 构建第1棵决策树：切分点6.5将样本分为两部分

  • 小于6.5的样本（$ x = 1, 2, 3, 4, 5, 6 $），输出值为-1.07
  • 大于6.5的样本（$ x = 7, 8, 9, 10 $），输出值为1.60

  

4.3.3 构建第2个弱学习器

• 计算负梯度（残差）：

  • 新的目标值为第1个弱学习器的负梯度

  • 计算结果如下：

    

• 寻找最优切分点：

  • 尝试不同的切分点（1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5），计算每个切分点的平方损失。

  • 平方损失计算公式：
    $$\text{平方损失}=\sum (y_i-f(x_i){)}^2$$

  • 计算结果如下：

    

  • 选择平方损失最小的切分点3.5，此时平方损失为0.79；

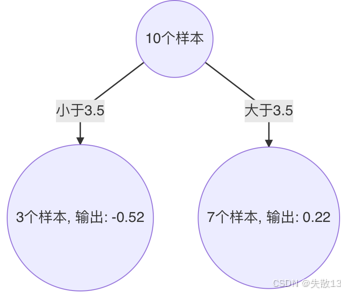
• 构建第2棵决策树：切分点3.5将样本分为两部分

  • 小于3.5的样本（$ x = 1, 2, 3 $），输出值为-0.52
  • 大于3.5的样本（$ x = 4, 5, 6, 7, 8, 9, 10 $），输出值为0.22

  

4.3.4 构建第3个弱学习器

1. 计算负梯度（残差）：

   • 新的目标值为第2个弱学习器的负梯度；

   • 计算结果如下：

     

2. 寻找最优切分点：

   • 尝试不同的切分点（1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5），计算每个切分点的平方损失。

   • 平方损失计算公式：
     $$\text{平方损失}=\sum (y_i-f(x_i){)}^2$$

   • 计算结果如下：

     

   • 选择平方损失最小的切分点6.5，此时平方损失为0.47；

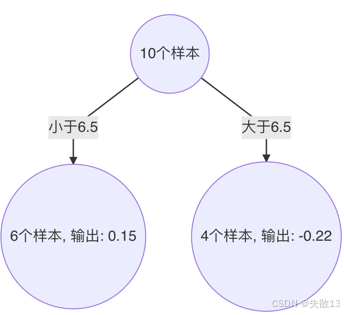
3. 构建第3棵决策树：切分点6.5将样本分为两部分

   • 小于6.5的样本（$ x = 1, 2, 3, 4, 5, 6 $），输出值为0.15
   • 大于6.5的样本（$ x = 7, 8, 9, 10 $），输出值为-0.22

   

4.3.5 构建最终弱学习器

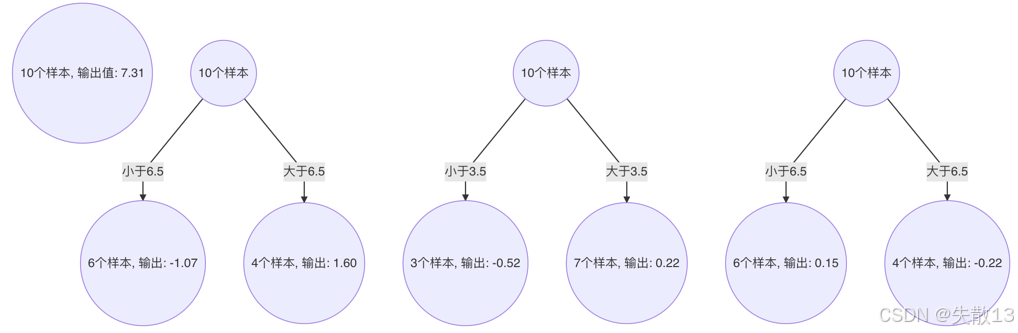
• 组合所有弱学习器：

  • 最终的强学习器由3个弱学习器组成，每个弱学习器的输出值相加得到最终预测值；

  • 以 $ x = 6 $为例：
    $$\text{最终预测值}=7.31+(-1.07)+0.22+0.15=6.61$$

  • 其他样本的预测值计算方式类似，结果：

    

  

4.4 梯度提升树的构建流程

1. 初始化弱学习器：使用目标值的均值作为初始预测值；
2. 迭代构建学习器：每个学习器拟合上一个学习器的负梯度（残差）；
3. 停止条件：直到达到指定的学习器个数；
4. 预测：当输入未知样本时，将所有弱学习器的输出结果组合起来作为强学习器的输出。

4.5 案例

• 导包：

  import pandas as pd
  from sklearn.model_selection import train_test_split
  from sklearn.ensemble import GradientBoostingClassifier
  

• 读取数据：

  # 1.读取数据
  data =pd.read_csv('data/titanic/train.csv')
  print(data.head())
  print(data.info())
  

• 数据处理：

  # 2.数据处理
  x = data[['Pclass','Sex','Age']].copy()
  y = data['Survived'].copy()
  print(x.head(10))
  x['Age'].fillna(x['Age'].mean(),inplace = True)
  print(x.head(10))
  x=pd.get_dummies(x)
  print(x.head(10))x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2)
  

• 模型训练：

  model =GradientBoostingClassifier()
  model.fit(x_train,y_train)
  print(model.score(x_test,y_test))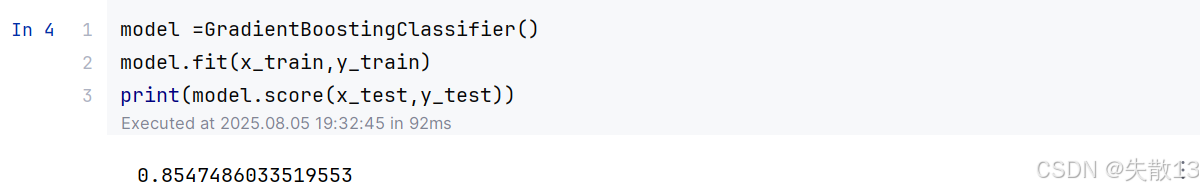
  

  

5 XGBoost算法

5.1 概述

• XGBoost（eXtreme Gradient Boosting）是一种极端梯度提升树，是集成学习方法中的王牌算法，在数据挖掘比赛中，大部分获胜者都使用了XGBoost；

• 构建思想：

  • 最小化训练数据的损失函数：
    $$\underset{f\in F}{\min }\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))$$

    • 其中，$ L(y_i, f(x_i)) $ 是损失函数，用于衡量预测值与真实值之间的差异；

  • 问题：仅最小化训练数据的损失函数会导致模型复杂度较高，容易过拟合；

  • 加入正则化项：
    $$\underset{f\in F}{\min }\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\Omega (f)$$

    • 其中，$ \Omega(f) $ 是正则化项，用于控制模型的复杂度，提高模型对未知测试数据的泛化性能；

• XGBoost其实是对GBDT的改进，在损失函数中加入了正则化项。目标函数为：
  $$\text{obj}(\theta )=\sum _{i=1}^{n}L(y_i,{\hat{y}}_i)+\sum _{k=1}^K\Omega (f_k)$$

  • 其中，$ \hat{y}_i $ 是预测值，$ f_k $ 是第 $ k $ 棵树，$ K $ 是树的数量；

• 正则化项：正则化项 $ \Omega(f) $ 用于降低模型的复杂度，其形式为：
  $$\Omega (f)=\gamma T+\frac{1}{2}\lambda \Vert w{\Vert }^2$$

  • 其中：$ \gamma T $ 中的 $ T $ 表示一棵树的叶子节点数量，$ \frac{1}{2} \lambda |w|^2 $ 中的 $ w $ 表示叶子节点输出值组成的向量，$ |w| $ 是向量的L2范数，$ \lambda $ 是对该项的调节系数。

5.2 示例

• 预测一家人对电子游戏的喜好程度：

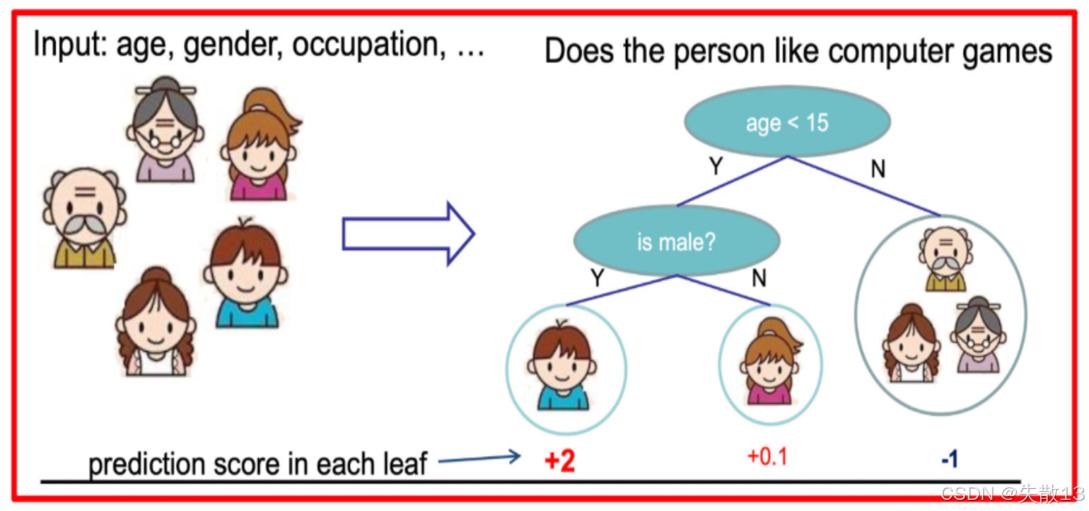
  • 考虑到年轻人和老年人相比，年轻人更可能喜欢电子游戏；以及男性和女性相比，男性更喜欢电子游戏。故先根据年龄大小区分小孩和大人，然后再通过性别区分开是男是女，逐一给各人在电子游戏喜好程度上打分

    

  • 决策树的结构：

    • 根节点：年龄是否小于15岁
    • 内部节点：性别是否为男性
    • 叶子节点：输出每个人的喜好程度得分

  • 上图得分分别为：+2（男孩）、+0.1（女孩）、-1（大人）

• 多棵树的组合：

  • 训练出两棵树（tree1和tree2），类似GBDT的原理，两棵树的结论累加起来便是最终的结论

    

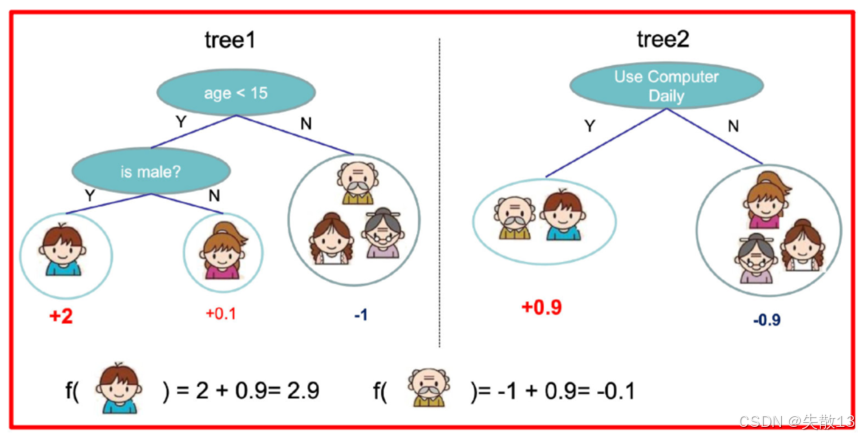
  • 图中的得分计算：

    • 男孩的最终得分为 $ 2 + 0.9 = 2.9 $
    • 老人的最终得分为 $ -1 + 0.9 = -0.1 $

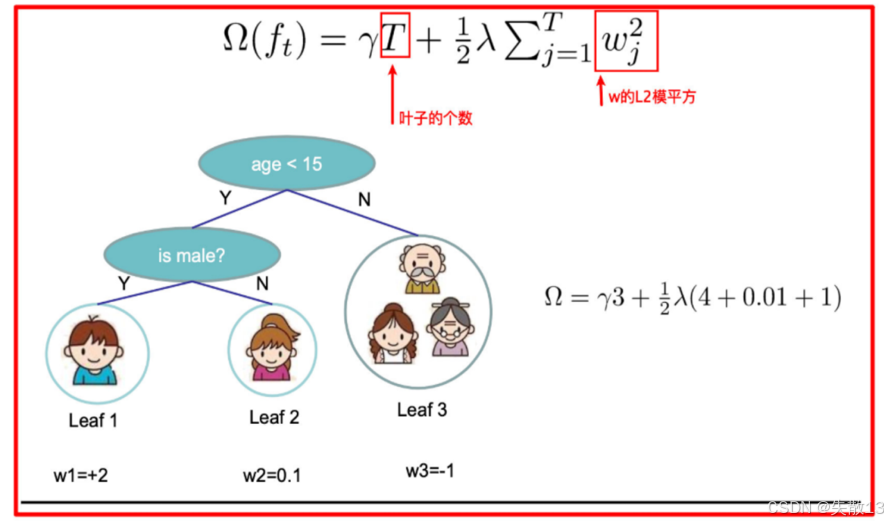
• 树的复杂度计算：以tree1为例，其复杂度为
  $$\Omega =\gamma \times 3+\frac{1}{2}\lambda \times (2^2+0.1^2+(-1{)}^2)$$

  • 其中，$ \gamma $ 是叶子节点数量的惩罚系数，$ \lambda $ 是L2正则化系数

  

5.3 XGBoost的目标函数

• t次迭代的学习模型目标函数：
  $${\text{obj}}^{(t)}=\sum _{i=1}^{n}L\left(y_i,{\hat{y}}_i^{(t)}\right)+\sum _{k=1}^t\Omega (f_k)$$

  • 其中，$ \hat{y}_i^{(t)} $ 是第 $ t $ 次迭代的预测值；

• 展开目标函数：
  $${\text{obj}}^{(t)}=\sum _{i=1}^{n}L\left(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i)\right)+\sum _{k=1}^{t-1}\Omega (f_k)+\Omega (f_t)$$

  • 其中，$ \hat{y}_i^{(t-1)} $ 是第 $ t-1 $ 次迭代的预测值，$ f_t(x_i) $ 是第 $ t $ 棵树的预测值；

• 泰勒展开近似：直接对目标函数求解比较困难，通过泰勒展开将目标函数换一种近似的表示方式。泰勒展开的目的是将复杂的损失函数近似为二次函数，从而可以更高效地求解。

5.4 泰勒展开

• 定义：泰勒展开是将一个函数在某一点处展开成无限项的多项式表达式。一般形式：
  $$f(x+\Delta x)=f(x)+f^{\prime }(x)\cdot \Delta x+\frac{1}{2}{f}^{\prime \prime }(x)\cdot \Delta x^2+\dots +\frac{1}{n!}{f}^{(n)}(x)\cdot \Delta x^n$$
• 一阶泰勒展开：
  $$f(x+\Delta x)\approx f(x)+f^{\prime }(x)\cdot \Delta x$$
• 二阶泰勒展开：
  $$f(x+\Delta x)\approx f(x)+f^{\prime }(x)\cdot \Delta x+\frac{1}{2}{f}^{\prime \prime }(x)\cdot \Delta x^2$$

5.5 XGBoost的目标函数推导

• 目标函数：

  • 进行 $ t $ 次迭代的学习模型目标函数为：
    $${\text{obj}}^{(t)}=\sum _{i=1}^{n}L\left(y_i,{\hat{y}}_i^{(t)}\right)+\sum _{k=1}^t\Omega (f_k)$$
  • 展开后：
    $${\text{obj}}^{(t)}=\sum _{i=1}^{n}L\left(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i)\right)+\sum _{k=1}^{t-1}\Omega (f_k)+\Omega (f_t)$$

• 泰勒二阶展开：

  • 目标函数对 $y_i^{t-1}$ 进行泰勒二阶展开，得到近似表示：
    $${\text{obj}}^{(t)}\approx \sum _{i=1}^n\left[L\left(y_i,{\hat{y}}_i^{(t-1)}\right)+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)\right]+\sum _{k=1}^{t-1}\Omega (f_k)+\Omega (f_t)$$

  • 其中，$ g_i $ 和 $ h_i $ 分别为损失函数的一阶导数和二阶导数：
    $$\begin{gathered} g_i=\frac{\partial L\left(y_i,{\hat{y}}_i^{(t-1)}\right)}{\partial {\hat{y}}_i^{(t-1)}} \\ {h}_i=\frac{{\partial }^{2}L\left(y_i,{\hat{y}}_i^{(t-1)}\right)}{\partial {\left({\hat{y}}_i^{(t-1)}\right)}^2} \end{gathered}$$

• 简化目标函数：

  • 去掉常数项（前 $ t-1 $ 个弱学习器的目标函数）：
    $${\text{obj}}^{(t)}\approx \sum _{i=1}^n\left[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)\right]+\Omega (f_t)$$
  • 代入正则化项 $ \Omega(f_t) = \gamma T + \frac{1}{2} \lambda |w|^2 $：
    $${\text{obj}}^{(t)}\approx \sum _{i=1}^n\left[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)\right]+\gamma T+\frac{1}{2}\lambda \Vert w{\Vert }^2$$

• 从样本角度转为叶子节点输出角度：

  • 目标函数中的各项可以转换为叶子节点的形式：
    $$\begin{gathered} \sum _{i=1}^n{g}_i{f}_t(x_i)=\sum _{j=1}^T\left(\sum _{i\in I_j}{g}_i\right)w_j \\ \sum _{i=1}^n\frac{1}{2}{h}_i{f}_t^2(x_i)=\frac{1}{2}\sum _{j=1}^T\left(\sum _{i\in I_j}{h}_i\right)w_j^2 \\ \frac{1}{2}\lambda \Vert w{\Vert }^2=\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2 \end{gathered}$$

    • 其中，$ I_j $ 表示第 $ j $ 个叶子节点的样本集合，$ w_j $ 表示第 $ j $ 个叶子节点的输出值；

• 转换后的目标函数：
  $${\text{obj}}^{(t)}\approx \sum _{j=1}^T\left[\left(\sum _{i\in I_j}{g}_i\right)w_j+\frac{1}{2}\left(\sum _{i\in I_j}{h}_i\right)w_j^2\right]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$

  • 合并同类项：
    $${\text{obj}}^{(t)}\approx \sum _{j=1}^T\left[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2\right]+\gamma T$$

    • 其中，$ G_j = \sum_{i \in I_j} g_i $，$ H_j = \sum_{i \in I_j} h_i $

• 目标函数的最优解：

  • 求导并令导数为0：对 $ w_j $ 求导并令导数为0，得到 $ w_j $ 的最优值
    $$w_j=-\frac{G_j}{H_j+\lambda }$$

  • 代入最优解求目标函数最小值：将 $ w_j $ 代入目标函数，得到最小值
    $${\text{obj}}^{(t)}=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$

• 该公式也叫做打分函数（Scoring Function）

  • 定义：

    • 目标函数的最小值也称为打分函数，用于衡量一棵树的优劣；
    • 打分函数的公式为（同上面的目标函数的最优解）：
      $${\text{obj}}^{(t)}=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$

  • 增益（Gain）计算：

    • 当构建树时，选择划分点的依据是增益（Gain），即分裂前后的打分函数之差：
      $$\text{Gain}={\text{obj}}_{L+R}-({\text{obj}}_L+{\text{obj}}_R)$$
    • 具体计算：
      $$\text{Gain}=\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma$$
    • 其中，$ G_L $ 和 $ H_L $ 是左子树的一阶导数和二阶导数之和，$ G_R $ 和 $ H_R $ 是右子树的一阶导数和二阶导数之和；

• 根据上面计算的 Gain 值，树的分裂条件如下：

  • 分裂判断：

    • 对树中的每个叶子节点尝试进行分裂
    • 计算分裂前后的增益：
      • 如果增益 $ > 0 $，则分裂后的损失更小，考虑此次分裂
      • 如果增益 $ < 0 $，则分裂后的损失更大，不建议分裂

  • 停止分裂的条件：

    • 达到最大深度
    • 叶子节点数量低于某个阈值
    • 所有节点在分裂后不能降低损失

5.6 API

• XGBoost的安装和使用

  • 在scikit-learn机器学习库中没有集成XGBoost，需要手动安装；

  • 使用pip命令安装：

    pip3 install xgboost
    

  • 可以在XGBoost的官方文档中查看最新版本：XGBoost官方文档；

• XGBoost的编码风格

  • 非sklearn方式：

    • XGBoost支持自己的编码风格，这种方式不依赖于scikit-learn库

    • 示例代码：

      import xgboost as xgb
      # 加载数据
      dtrain = xgb.DMatrix('train.csv?format=csv&label_column=0')
      dtest = xgb.DMatrix('test.csv?format=csv&label_column=0')
      # 设置参数
      param = {'max_depth': 2, 'eta': 1, 'objective': 'binary:logistic'}
      # 训练模型
      bst = xgb.train(param, dtrain)
      # 预测
      preds = bst.predict(dtest)
      

  • sklearn方式：

    • XGBoost也支持scikit-learn的编码风格，调用方式与scikit-learn保持一致
    • 示例代码：

      from xgboost import XGBClassifier
      from sklearn.model_selection import train_test_split
      from sklearn.metrics import accuracy_score
      # 加载数据
      X, y = load_data()
      X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
      # 初始化模型
      model = XGBClassifier(max_depth=2, learning_rate=1, objective='binary:logistic')
      # 训练模型
      model.fit(X_train, y_train)
      # 预测
      y_pred = model.predict(X_test)
      # 评估模型
      accuracy = accuracy_score(y_test, y_pred)
      print(f"Accuracy: {accuracy}")
      

5.7 案例

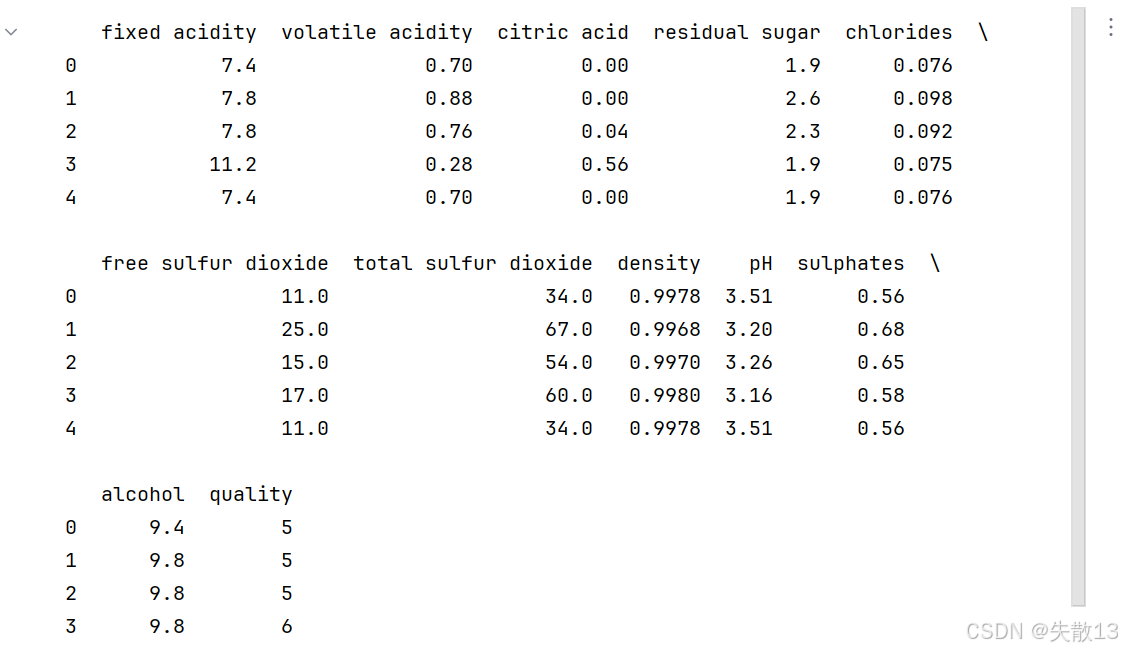
• 数据集共包含 11 个特征，共计 3269 条数据。我们通过训练模型来预测红酒的品质，品质共有 6个类别，分别使用数字：0、 1、2、3、4、5 来表示

  

• 导包：

  import pandas as pd
  from sklearn.model_selection import train_test_split
  from xgboost import XGBClassifier
  from sklearn.metrics import classification_report
  from sklearn.utils import class_weight
  from sklearn.ensemble import GradientBoostingClassifier
  

• 数据处理：

  # 数据处理
  data =pd.read_csv('./data/红酒品质分类.csv')
  print(data.head())
  # 提取特征数据：选取所有行，除最后一列外的所有列作为特征x
  x = data.iloc[:,:-1]
  # 提取标签数据：选取所有行的最后一列作为标签y，并将标签值减去3（可能是为了将标签值映射到更小的范围，如0开始的整数）
  y = data.iloc[:,-1]-3x_train,x_test,y_train,y_test=train_test_split(x,y,stratify=y,test_size=0.2)# 将训练集的特征x_train和标签y_train按列拼接（axis=1表示列拼接），并保存为CSV文件
  pd.concat([x_train,y_train],axis=1).to_csv('红酒品质分类_train.csv')
  pd.concat([x_test,y_test],axis=1).to_csv('红酒品质分类_test.csv')
  

• 数据获取：

  # 数据获取
  train_data = pd.read_csv('红酒品质分类_train.csv')
  test_data = pd.read_csv('红酒品质分类_test.csv')# 从训练集中提取特征数据：所有行，除最后一列外的所有列
  x_train = train_data.iloc[:, :-1]
  # 从训练集中提取标签数据：所有行的最后一列
  y_train = train_data.iloc[:, -1]
  x_test = test_data.iloc[:, :-1]
  y_test = test_data.iloc[:, -1]# 计算样本权重：使用'balanced'模式自动调整权重，解决类别不平衡问题
  # 对于样本较少的类别会赋予更高权重，样本较多的类别赋予较低权重
  class_weight = class_weight.compute_sample_weight(class_weight='balanced', y=y_train)
  

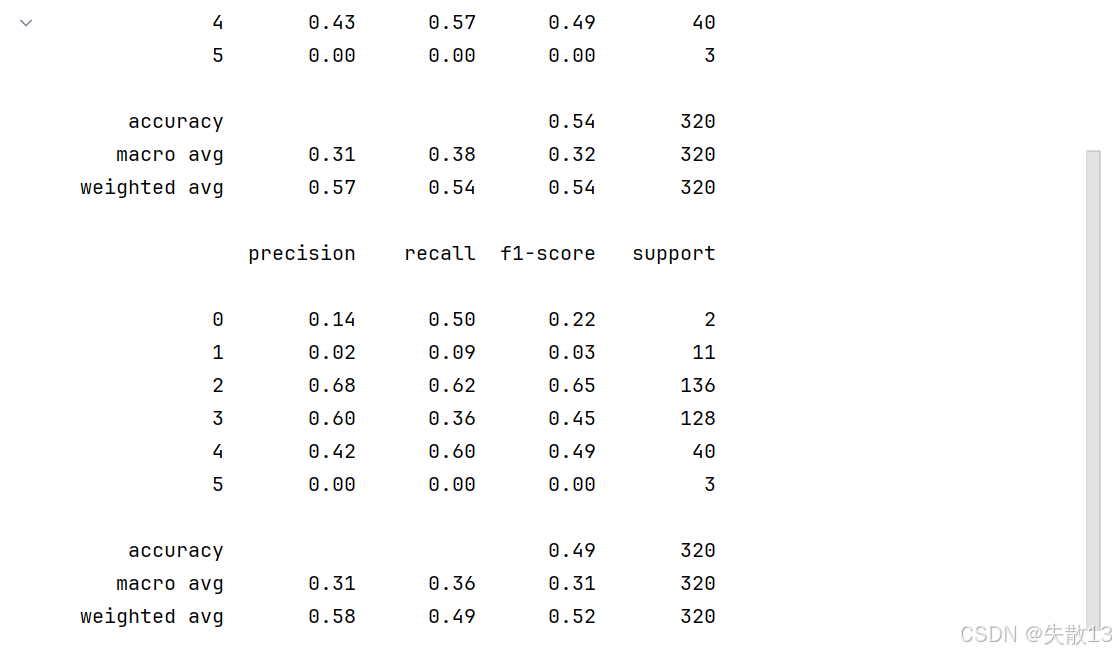
• 模型训练：

  # 模型训练
  # 初始化XGBoost分类器，设置树的数量为5，多分类目标函数为'softmax'（直接输出类别）
  model1 = XGBClassifier(n_estimators=5, objective='multi:softmax')
  # 初始化GBDT分类器，设置树的数量为5
  model2 = GradientBoostingClassifier(n_estimators=5)
  model1.fit(x_train, y_train, sample_weight=class_weight)
  model2.fit(x_train, y_train, sample_weight=class_weight)y_pre1 = model1.predict(x_test)
  y_pre2 = model2.predict(x_test)print(classification_report(y_test, y_pre1))
  print(classification_report(y_test, y_pre2))