当前位置：首页 > news >正文

CS231n2017 Lecture14 强化学习笔记

news 2025/8/8 11:48:13

强化学习：

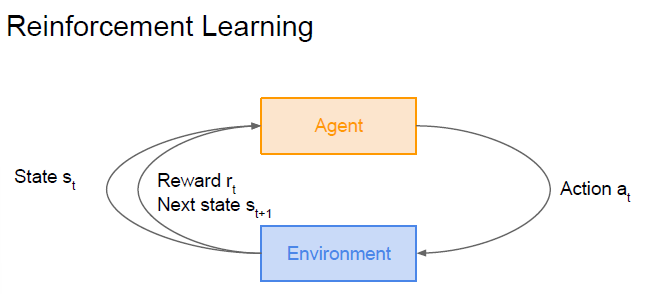
强化学习包含2个可以进行交互的对象：智能体(Agent)和环境(Environment)

Agent:

可以感知Environment的状态(state)，根据反馈的奖励(Reward)，学习一个合适的动作(Action)，希望能够最大化长期总收益

Environment:

Environment会接受Agent执行的一系列动作，将这一系列动作进行评价，并转换为一种可量化的信号，反馈给Agent

除此之外，还有其他核心要素：

策略(Policy):

Agent在Environment中特定时间的行为方式，可以看作Environment的state到action的映射

回报函数(Reward Function):

Agent在Environment中的每一步，Environment都会通过Reward Function向Agent发送一个标量数值，即Reward

价值函数(Value Function):

表示从长远的角度来看，什么state是好的，一个state的value就是Agent从这个state开始，对将来积累的总收益的期望

马尔科夫决策过程(Markov Decision Process):

我们的问题时候hi如何形式化定义RL问题，使之支持推断，最常用的是Markov决策过程

假象一个agent在面对某种场景(比如围棋游戏)，所处的环境可以定义为state(白棋和黑棋的数量和位置，到谁出棋)，agent能够在environment中采取action，这些action会导致一些reward，然后action会导致新的state，agent又会在新的state中继续采取action，采取action的原则叫做policy

那么一系列的state,action,reward就构成了一个Markov决策过程，一个Markov决策过程（比如一把游戏），由一串有限个数的state,action,reward组成，即：

$s_0,a_0,r_1,s_1,a_1,r_2,s_2,...,s_{n-1},a_{n-1},r_n,s_n$

其中 $s_i$ 为第i个状态， $a_i$ 为第i个动作， $r_{i+1}$ 表示进行 $a_i$ 后获得的奖励， $s_n$ 是终止状态，这个转移过程建立在Markov假设之上，即下个时刻的 $s_{i+1}$ 只与当前状态 $s_i$ 和动作 $a_i$ 有关，与之前的状态及动作无关

打折的未来奖励(discount factor):

为了在长期决策过程中表现得更好，采取一个动作时，我们不仅要考虑这个动作导致的即时reward，还要考虑这个动作到之后的未来reward

给定一个Markov决策过程，其对应的奖励总和如下：

$R=\sum_{i=1}^nr_i$

而t时刻的未来奖励如下：

$R_t = \sum_{i=t}^nr_i$

由于agent所处的environment非常复杂，我们甚至无法确定在两次采取相同action后,agent能够获得相同的reward，agent在未来进行的动作越多，其获得reward的变化应当越大，因此，我们一般采用打折的未来奖励作为t时刻未来奖励的替代，即：

$R_t = \sum_{i=t}^n\gamma^{i-t}r_i$

其中 $\gamma$ 是0到1之间的折扣因子，其是我们更少地考虑过于长远的reward,由上述定义，我们可以得到递推式：

$R_t = r_t + \gamma R_{t+1}$

若 $\gamma$ 越小，我们就采取越短视的策略，也就是更大程度地忽略未来奖励， $\gamma$ 越大则相反

如此定义，对于agent来说，好的策略应当是它在各个环境下，能够采取使得 $R_t$ 最大的action

Q-Learning算法

我们定义一个 $Q(s,a)$ 函数，表示agent在s状态下采取行动a，并在之后采取最优行动的条件下获得的打折的未来奖励，即

$Q(s_t,a_t) = max_{\pi}R_{t+1}$

该函数反映了在s状态下a行动的质量(Quality)

这样一来，我们就可以定义最优策略 $\pi$ ，其中

$\pi(s) = argmax_a Q(s,a)$

我们该如何获得Q函数呢？让我们来考虑一个转移 $<s,a,r,s^{'}>$ ，则会有Bellman公式：

$Q(s,a) = r + \gamma max_{a^{'}}Q(s^{'},a^{'})$

即最大化未来奖励相当于最大化即时奖励和下一状态的最大未来奖励之和，那么我们可以通过迭代的方式，使这个Q函数收敛，从而逼近学习Q函数

即 $Q_{i+1}(s,a) = r + \gamma max_{a^{'}}Q_i(s^{'},a^{'})$ ，其中i为迭代次数

当 $i \to \infty$ 时， $Q_i \to Q^*$

具体更新公式：

$Q(s,a) = Q(s,a) + \alpha (r+\gamma max_{a^{'}}Q(s^{'},a^{'})-Q(s,a))$

缺点：

当state非常多的时候，我们就很难通过迭代计算覆盖整个Q函数的空间，因此我们需要使用更好地逼近方式去估计Q函数，这里选择使用神经网络

Deep Q Network:

如上述所说，我们使用神经网络来对Q函数建模，比如我们搭建一个神经网络，它接受一个状态（可能是连续四帧的屏幕截图），并输出所有动作对应的Q值，那么这显然是一个回归问题

测试过程：

agent观察当前状态 $s_t$

将 $s_t$ 输入到当前Q网络，参数为 $\theta$

Q网络输出所有动作的预测Q值 $Q(s_t,a;\theta)$

agent采用 $\epsilon-greedy$ 策略选择动作执行：

以 $\epsilon$ 概率随机选择一个动作（探索）

以 $1-\epsilon$ 的概率选择预测Q值最大的动作，即 $argmax_{a}Q(s_t,a;\theta)$

经验储存(Experience Replay):

agent将这次交互的经验 $(s_t,a_t,r_t,s_{t+1},done)$ 储存到一个固定大小的回放缓冲区

其中done表示该次episode是否结束

缓冲区就像一个队列，当存满时，最旧的经验会出队，而新的经验会入队

网络训练：

定期（每隔若干步）或当缓冲区积累了一定的经验后，开始训练

随机采样：

从回放缓冲区D中随机均匀地抽取一小批(mini-batch)经验样本，这样做可以打破样本之间的时间相关性（时间连续的样本高度相关），使训练更稳定，数据利用更高效

计算目标Q值：

如果done==True，则说明下一状态为终止态，则目标Q值为即时奖励，y=r

否则， $y = r + \gamma max_{a^{'}}Q(s^{'},a^{'},\theta^-)$ $\pi_{\theta}$

这里的 $\theta^-$ 是目标网络(target)的参数，目标网络与主Q网络的结构完全相同，但其参数 $\theta^-$ 在一段时间后（如每N步），才从主Q网络 $\theta$ 同步一次，平时保持不变，这是DQN稳定训练的关键

计算Loss：

通常使用MSE，衡量当前Q网络所选动作a的预测值 $Q(s,a;\theta)$ 与上述预测的目标值y之间的差距

即： $L(\theta) = [y-Q(s,a;\theta)]^2$

Loss只针对样本中实际执行过的动作a计算，对于该状态下的其他未执行动作，不计算它们的loss

更新主Q网络：

反向传播梯度下降更新 $\theta$

伪代码如下：

梯度策略(Policy Gradient):

我们这里舍弃Q函数，因为使用Q函数的本质是基于动作的Q价值来选择动作，那么我们希望搭建一个函数，其输入是状态，输出直接就是动作

首先，让我们定义一个参数化的策略集合 $\Pi = \{ \pi_{\theta},\theta\in R^m\}$

那么我们对每一个策略 $\pi_{\theta}$ ，我们定义一个函数来衡量其好坏

$J(\theta) = E[\sum_{t \ge0}\gamma^t r_t | \pi_{\theta}]$ ，其中 $r_t$ 为第t步所获得的奖励，那么我们的优化目的就变成了

找到 $\theta^* = argmax_{\theta}J(\theta)$ ，这里可以通过梯度上升的方法来优化参数

那么我们定义 $\tau = (s_0,a_0,r_0,s_1,...)$ 是一条状态转移路径

那么 $J(\theta) = \int_{\tau}r(\tau)p(\tau;\theta)d\tau$

则 $\nabla_{\theta}J(\theta) = \int_{\tau}r(\tau)\nabla_{\theta}p(\tau;\theta)d\tau = E_{\tau\sim p(\tau;\theta)}[r(\tau)\nabla_{\theta}logp(\tau;\theta)]$

其中用到了 $\nabla_{\theta}p(\tau;\theta) = p(\tau;\theta)\frac{\nabla_{\theta}p(\tau;\theta)}{p(\tau;\theta)} = p(\tau;\theta)\nabla_{\theta}logp(\tau;\theta)$

那么现在问题就在于如何去表示 $p(\tau;\theta)$

由 $p(\tau;\theta) = \prod_{t \ge 0 }p(s_{t+1}|s_t,a_t)\pi_{\theta}(a_t|s_t)$ ，其中 $\pi_{\theta}(a_t|s_t)$ 为在状态 $s_t$ 条件下作出 $a_t$ 动作的概率

则 $logp(\tau;\theta) = \sum_{t \ge 0}logp(s_{t+1}|s_t,a_t)+log\pi_{\theta}(a_t|s_t)$

则 $\nabla_{\theta}logp{(\tau;\theta)} = \sum_{t \ge 0}\nabla_\theta log\pi_{\theta}(a_t|s_t)$

因此，当我们采样出一个路径 $\tau$ 时，我们就可以估计loss的梯度为:

$\nabla_\theta J(\theta) \approx \sum_{t \ge 0}r(\tau)\nabla_{\theta}log\pi_{\theta}(a_t|s_t)$

这样一来，当一个路径 $\tau$ 的收益高时，我们就提高其出现的概率，否则降低其概率

可以发现，用一条路径的收益来评价这条路径上所有动作的好坏可能过于简单了，但在期望上来讲，它会平均掉动作质量的好坏

减少方差的梯度策略算法形式：

$g = E[\sum_{t \ge 0}\Psi_t\nabla_{\theta}log\pi_{\theta}(a_t|s_t)]$

其中 $\Psi_t$ 为t时刻的评价指标，可能是如下的形态：

$\sum_{t \ge 0}r_t$

$\sum_{t^{'}=t}r_{t^{'}}$

$\sum_{t^{'}=t}\gamma ^ {t^{'}-t}r_{t^{'}}$

$\sum_{t^{'} = t}r_{t^{'}}-b(s_t)$

其中 $b(s_t)$ 为baseline，一个简单的baseline选择策略是选取目前经历过的所有路径的奖励的滑动平均

$A^{\pi_\theta}(s_t,a_t)=Q^{\pi_{\theta}}(s_t,a_t)-V^{\pi_{\theta}}(s_t)$

优势函数，其中 $V^{\pi_\theta} = E_{s_{t+1} \to \infty}[\sum_{t^{'}=t}r_{t^{'}}]$ ， $Q^{\pi_{\theta}}(s_t,a_t) =E_{a_{t+1} \to \infty} \sum_{t^{'} = t}r_{t^{'}}$