机器学习第六课之贝叶斯算法
简介
所谓的贝叶斯定理源于他生前为解决一个“逆概”问题写的一篇文章,而这篇文章是在他死后才由他的一位朋友发表出来的。在贝叶斯写这篇文章之前,人们已经能够计算“正向概率”,如“假设袋子里面有 N 个白球,M 个黑球,你伸手进去摸一把,摸出黑球的概率是多大”。而一个自然而然的问题是反过来:“如果我们事先并不知道袋子里面黑白球的比例,而是闭着眼睛摸出一个(或好几个)球,观察这些取出来的球的颜色之后,那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。这个问题,就是所谓的逆向概率问题。
贝叶斯定理的思想出现在18世纪,但真正大规模派上用途还得等到计算机的出现。因为这个定理需要大规模的数据计算推理才能凸显效果,它在很多计算机应用领域中都大有作为,如自然语言处理,机器学习,推荐系统,图像识别,博弈论等等。我们今天说的也就是最简单的贝叶斯在机器学习上的使用朴素贝叶斯
一、贝叶斯算法原理详解
贝叶斯定理:
正向概率:
假设袋子里有 10 个白球,90 个黑球,然后从袋子里面拿出一个球,拿出的球是白球的概率是多少?
p (摸出白球)=10/100=1/10
逆向概率:
如果我们事先并不知道袋子里白球、黑球的比例,然后通过多次试验,根据拿出来球的颜色推测袋子里白球、黑球的比例。
题目:
在一个学校里面,男生占 60%,女生占 40%;男生:100% 穿长裤,女生:50% 穿长裤,50% 穿裙子;此时迎面走来一个穿长裤的学生,刚好你是高度近视,那么要判断一下这个穿长裤的学生是女生的概率该怎么计算?
实质:
穿长裤的是女生的概率 = 女生中穿长裤的人数 / 穿长裤的总人数
假设:
全校人数(U):1000 人。
男生中穿长裤的人数:
U×P (男生)×P (穿长裤 | 男生)=1000×60%×100%=600 (人)
女生中穿长裤的人数:
U×P (女生)×P (穿长裤 | 女生)=1000×40%×50%=200 (人)
穿长裤且是女生的概率:
200/(200+600)=25%
贝叶斯算法
实质:
穿长裤的是女生的概率 = 女生中穿长裤的人数 / 穿长裤的总人数
定义:
A— 男生 B— 女生 C— 穿长裤
那么:
P (B|C)=[U×P (B)×P (C|B)]/[U×P (A)×P (C|A)+U×P (B)×P (C|B)]
=[P (B)×P (C|B)]/P (C)
=(40%×50%)/(60%+40%×50%)
=25%
P (C)=[P (B)×P (C|B)]/P (C)
那贝叶斯如何将样本数据进行计算实现预测的?
示例:一个包含 3 个特征(A、B 和 C)和一个类别标签(D)的简单数据集
| 特征 A | 特征 B | 特征 C | 类别 D |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
- 目标:使用朴素贝叶斯分类器来预测一个新的样本(特征 A=1,特征 B=1,特征 C=0)的类别?。特征 A=0,特征 B=0,特征 C=1 属于?
- 核心:把输入当作条件,结果为 0 的概率是多大?结果为 1 的概率是多大?
- 公式:
首先,我们计算类别的先验概率:
然后,我们计算每个特征在每个类别下的条件概率:
现在,我们使用朴素贝叶斯分类器来计算给定特征值下每个类别的后验概率:
所以特征( A=1,特征 B=1,特征 C=0)的类别(D=0)的,由此可见贝叶斯算法是用于分类都算法
二、朴素贝叶斯的API
class sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)参数:
-
alpha:
这是一个非负浮点数,用于控制平滑操作的强度,默认值为 1.0。- 平滑的核心目的是避免模型在遇到训练数据中未出现的特征组合时,计算出 "零概率"(这会导致整个后验概率计算结果为零,影响分类)。
- 当
alpha=1.0时,称为拉普拉斯平滑(Laplace smoothing),会给所有特征的计数加 1; - 当
0 < alpha < 1时,称为利德斯通平滑(Lidstone smoothing),平滑强度弱于拉普拉斯平滑; - 当
alpha=0时,不进行平滑(不建议在实际场景中使用,可能因数据稀疏导致概率计算异常)。
-
fit_prior:
布尔值参数,默认值为True,用于控制是否根据训练数据计算先验概率。- 当
fit_prior=True时,模型会从训练样本中统计每个类别的占比,作为先验概率(例如,若训练集中 60% 的样本属于类别 A,则P(A)=0.6); - 当
fit_prior=False时,模型会假设所有类别的先验概率相等(即 "等先验",例如二分类问题中P(A)=P(B)=0.5)。
- 当
-
class_prior:
可选参数,默认值为None,用于手动指定每个类别的先验概率。- 若传入一个列表或数组,则列表中的元素需与类别一一对应(例如二分类中
class_prior=[0.3, 0.7]表示两个类别的先验概率分别为 0.3 和 0.7); - 若为
None,则先验概率由fit_prior参数控制(自动从数据中学习或使用等先验)。
- 若传入一个列表或数组,则列表中的元素需与类别一一对应(例如二分类中
对于朴素贝叶斯这些参数一般使用默认值
三、案例分析:
对于朴素贝叶斯算法,该算法的准确率相对于没有那么高,我们重点学习这个算法的思想,下面我就以手写识别为一个案例简单说明一下朴素贝叶斯的使用。
使用 scikit-learn 库实现了基于多项式朴素贝叶斯(MultinomialNB)的手写数字识别分类任务
导入必要的库:
from sklearn.datasets import load_digits
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn import metrics加载并准备数据:
digits = load_digits() # 加载手写数字数据集
x = digits.data # 获取特征数据(图像的像素特征)
y = digits.target # 获取标签数据(对应的数字类别,0-9)数据集包含 8x8 像素的手写数字图像,每个图像被转换为 64 维的特征向量(8×8)。
分割数据集:
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0
)- 将数据分为训练集(80%)和测试集(20%)
test_size=0.2表示测试集占比 20%random_state=0固定随机种子,确保结果可复现
创建并训练模型:
estimator = MultinomialNB(alpha=1) # 创建多项式朴素贝叶斯模型,使用拉普拉斯平滑
estimator.fit(x_train, y_train) # 用训练数据拟合模型alpha=1表示使用拉普拉斯平滑,避免零概率问题
模型预测与评估:
test_predicted = estimator.predict(x_test) # 用训练好的模型预测测试集
scores = estimator.score(x_test, y_test) # 计算模型在测试集上的准确率
print(scores) # 输出准确率
print(metrics.classification_report(y_test, test_predicted)) # 输出详细分类报告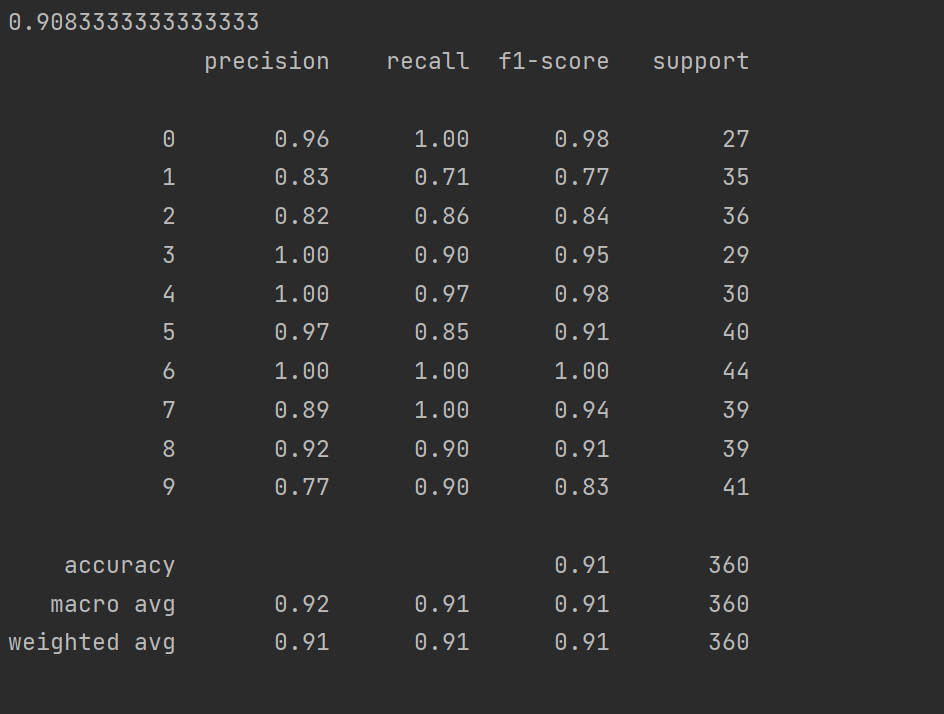
输出结果说明:
- 第一个输出是模型的准确率(accuracy),即正确分类的样本占总样本的比例
- 第二个输出是详细的分类报告,包含:
- 每个类别的精确率(precision)、召回率(recall)、F1 分数(F1-score)
- 每个类别的支持样本数(support)
- 整体的宏平均(macro avg)和加权平均(weighted avg)指标
