三种灰狼算法求解无人机三维路径规划【MATLAB实现】

1. 三种算法对比的无人机三维路径规划

2. 在三维空间中为无人机规划最优飞行轨迹，需避开障碍物、地形并满足动力学约束，目标是最小化飞行时间/距离或最大化安全性。

3. 多无人机作战规划
   针对多架无人机的协同任务（如侦察、打击），进行任务分配、路径规划和资源调度，确保整体作战效能最优。

4. 协同规划与协同突防

   • 协同规划：多无人机通过信息共享实现协作式路径规划，避免碰撞并优化群体行为。

   • 协同突防：多机配合突破敌方防御系统（如雷达网），通过分散诱饵、电磁干扰等策略提高生存率。

5. 

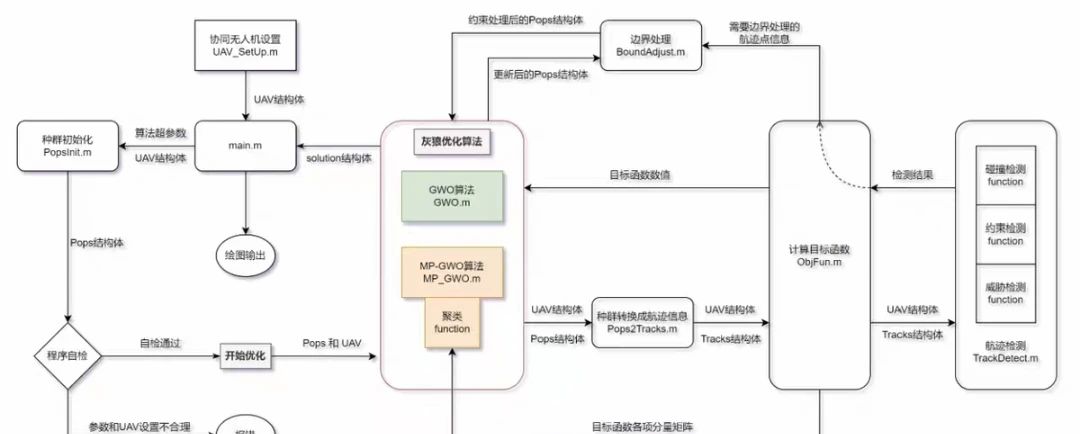
7. 优化算法对比

   • 灰狼优化算法 (GWO)：模拟灰狼群体狩猎行为的元启发式算法，适用于连续优化问题。

   • 多种群灰狼优化 (MP_GWO)：引入多个子种群并行搜索，增强全局寻优能力，避免早熟收敛。

• 布谷鸟灰狼算法 (CS_GWO) ：是一种混合元启发式优化算法CS_GWO 旨在融合 CS 强大的全局探索能力（通过莱维飞行实现大范围跳跃）和 GWO 强大的局部开发能力（通过狼群协作精确逼近最优解）。平衡搜索：通过特定的混合策略（如用 CS 的莱维飞行更新部分 GWO 中的狼位置，或在迭代过程中交替/结合两种机制），让算法在探索新区域和精细搜索已知有希望区域之间取得更好的平衡。

程序实例：

.rtcContent { padding: 30px; } .lineNode {font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }function solution = CS_GWO(UAV, SearchAgents, Max_iter)%CS_GWO 灰狼-布谷鸟优化算法%Gray Wolf Cuckoo Optimization% 超参数pa = 0.25;   % 布谷鸟搜索参数% 算法初始化[WolfPops, Tracks] = PopsInit(UAV, SearchAgents, false);   % 随机生成 初始狼群 和 轨迹们dim = WolfPops.PosDim;                                                         % 状态变量维度% 初始化解Alpha_pos = zeros(1, dim);   % α解Alpha_score = inf;                  % α解适应度Alpha_no = 1;                         % α解编号Beta_pos = zeros(1, dim);      % β解Beta_score = inf;                     % β解适应度Beta_no = 1;                             % β解编号Delta_pos = zeros(1, dim);     % δ解Delta_score = inf;                    % δ解适应度Delta_no = 1;                           % δ解编号Fitness_list = zeros(1, Max_iter);% 迭代求解ticfprintf('>>CS_GWO 优化中    00.00%%')for iter = 1 : Max_iter% ①  计算每只狼的适应度，更改其种群等级ProbPoints = cell(SearchAgents, 1);   for i = 1 : SearchAgents% 计算目标函数[fitness, ~, Data] = ObjFun(Tracks{i}, UAV);    % 一个智能体的目标函数ProbPoints{i} = Data.ProbPoint;                       % 所有智能体不符合条件的状态% 更新 Alpha、Beta 和 Delta 解if fitness <= Alpha_score  % 适应能力最强（因为性能指标越小越好，因此为小于号）Alpha_score = fitness;Alpha_pos = WolfPops.Pos(i, :);Alpha_no = i;end if fitness > Alpha_score && fitness <= Beta_scoreBeta_score = fitness;Beta_pos = WolfPops.Pos(i, :);Beta_no = i;endif fitness > Alpha_score && fitness > Beta_score && fitness <= Delta_scoreDelta_score = fitness;Delta_pos = WolfPops.Pos(i, :);Delta_no = i;endend% ②  更新参数aa = 2 - iter * 2 / Max_iter;                  % 线性递减%a = 2 * cos((iter / Max_iter) * pi/2);   % 非线性递减% ③  更新位置（朝着前三只狼位置前进）for i = 1 : SearchAgentsfor j = 1 : dimr1 = rand();r2 = rand();A1 = 2*a*r1 - a;C1 = 2*r2;D_alpha = abs(C1*Alpha_pos(j) - WolfPops.Pos(i, j));X1(i, j) = Alpha_pos(j) - A1*D_alpha;r1 = rand();r2 = rand();            A2 = 2*a*r1 - a;C2 = 2*r2;D_beta = abs(C2*Beta_pos(j) - WolfPops.Pos(i, j));X2(i, j) = Beta_pos(j) - A2*D_beta;r1 = rand();r2 = rand();A3 = 2*a*r1 - a;C3 = 2*r2;D_delta = abs(C3*Delta_pos(j) - WolfPops.Pos(i, j));X3(i, j) = Delta_pos(j) - A3*D_delta;%更新%WolfPops.Pos(i, j) = (X1(i, j) + X2(i, j) + X3(i, j)) / 3;endend% ④  Cuckoo 搜索fitness = nan(SearchAgents, 1);for i = 1 : SearchAgents[fitness(i), ~, ~] = ObjFun(Tracks{i}, UAV);end[~, index] = min(fitness);best = WolfPops.Pos(index, :);X1 = get_cuckoos(X1, best, WolfPops.lb, WolfPops.ub); X2 = get_cuckoos(X2, best, WolfPops.lb, WolfPops.ub);X3 = get_cuckoos(X3, best, WolfPops.lb, WolfPops.ub);X1 = empty_nests(X1, WolfPops.lb, WolfPops.ub, pa);X2 = empty_nests(X2, WolfPops.lb, WolfPops.ub, pa);X3 = empty_nests(X3, WolfPops.lb, WolfPops.ub, pa);WolfPops.Pos = (X1 + X2 + X3) / 3;% ⑤  调整不符合要求的状态变量[WolfPops, Tracks] = BoundAdjust(WolfPops, ProbPoints, UAV);% ⑥  存储适应度Fitness_list(iter) = Alpha_score;if iter/Max_iter*100 < 10fprintf('\b\b\b\b\b%.2f%%', iter/Max_iter*100)elsefprintf('\b\b\b\b\b\b%.2f%%', iter/Max_iter*100)endendfprintf('\n\n>>计算完成！\n\n')toc% 输出值solution.method = 'GWO';                % 算法solution.WolfPops = WolfPops;       % 所有解种群信息solution.Tracks = Tracks;                  % 所有解航迹信息solution.Fitness_list = Fitness_list;   % α解适应度曲线solution.Alpha_Data = Data;            % α解的威胁信息solution.Alpha_no = Alpha_no;        % α解的位置solution.Beta_no = Beta_no;             % β解的位置solution.Delta_no = Delta_no;          % δ解的位置end%%%%% 布谷鸟搜索 %%%%%function nest = get_cuckoos(nest, best, Lb, Ub)n = size(nest, 1);beta = 3/2;sigma = (gamma(1 + beta) * sin(pi*beta/2)/(gamma((1 + beta)/2)*beta*2^((beta - 1)/2)))^(1/beta);for j = 1:ns = nest(j, :);u = randn(size(s))*sigma;v = randn(size(s));step = u./abs(v).^(1/beta);stepsize = 0.01*step.*(s - best);s = s + stepsize.*randn(size(s));nest(j, :) = BoundClamp(s, Lb, Ub);endendfunction new_nest = empty_nests(nest, Lb, Ub, pa)n = size(nest, 1);K = rand(size(nest)) > pa;stepsize = rand*(nest(randperm(n), :) - nest(randperm(n), :));new_nest = nest + stepsize.*K;for j = 1:size(new_nest, 1)s = new_nest(j, :);new_nest(j, :) = BoundClamp(s, Lb, Ub);endendfunction x = BoundClamp(x, lb, ub)Flag4ub = x > ub;Flag4lb = x < lb;x = x .* ( ~(Flag4ub + Flag4lb) ) + ub .* Flag4ub + lb .* Flag4lb;end

运行结果：

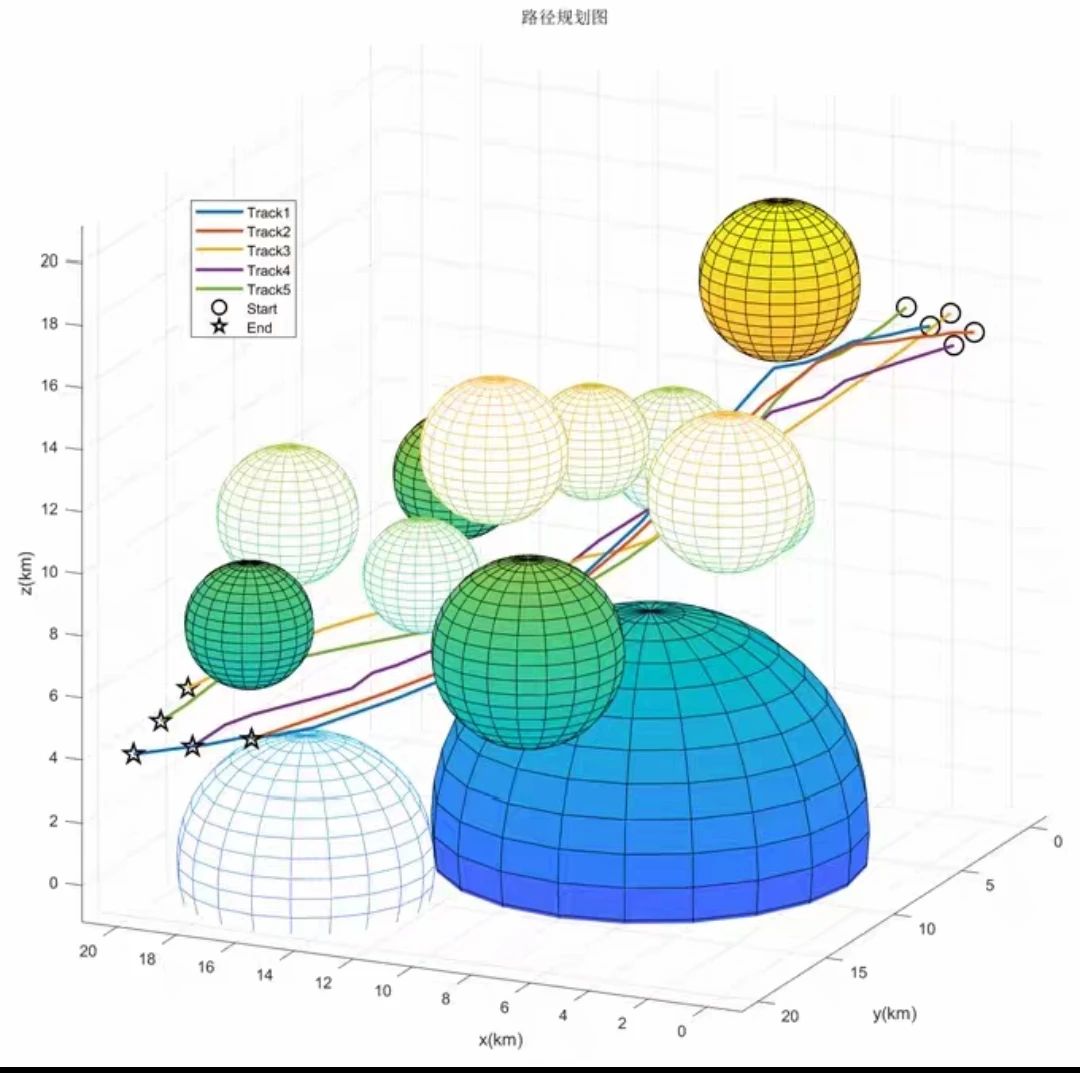
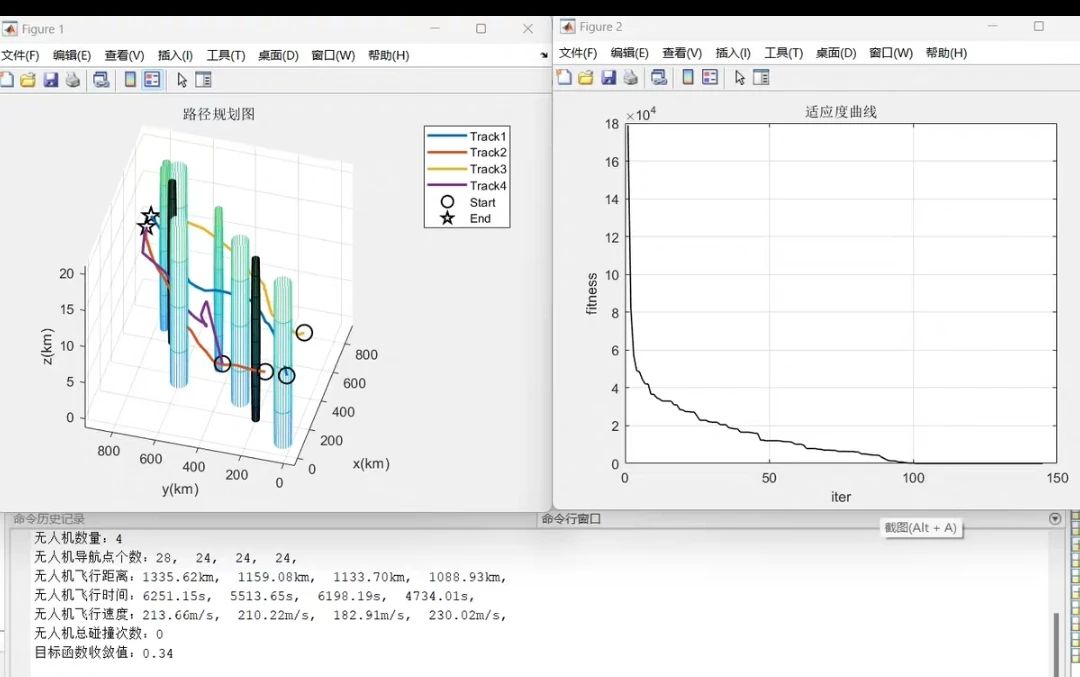
算法实现详情见原文链接：

https://mp.weixin.qq.com/s/vRKkzlrEQ1HRNgjRL8wYOQ