人工智能之数学基础:几何型(连续型)随机事件概率
本文重点
在前面的课程中,我们学习了离散型随机事件概率,接下来我们将学习几何型随机事件概率。
什么是几何型随机事件概率?
几何型概率定义在无限不可数集上,根据测度值(长度、面积、体积)定义。事件A发生的概率为区域A的测度值与Ω测度值的比值:
P(A)=S(A)/S(Ω)
其中S(A)为事件A的测度,S(Ω)为整个样本空间的测度。
一个简单的例子
现在有一个正方形0≤x,y≤1,在这个正方形内部随机扎一个点,这个点扎到任意处的可能性相等,那么该点扎在x≤0.5,y≤0.5的概率是多少?
P(x≤0.5,y≤0.5)=(0.5*0.5)/(1*1)=0.25
通过可视化的方式,可以看到其实就是两个区域的面积比例:
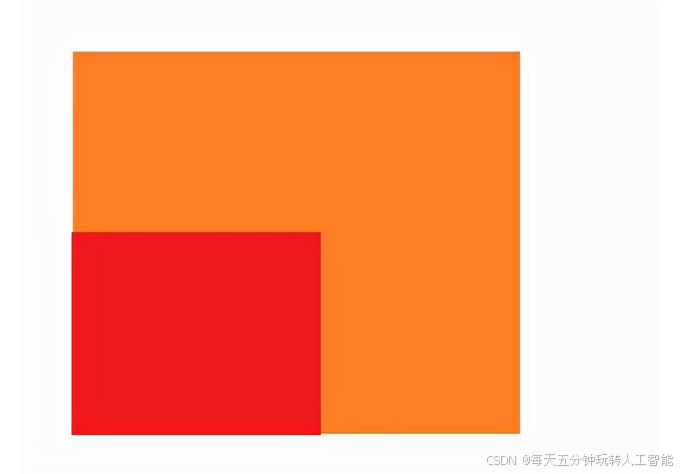
通过这个图像可以清楚地看到,红色区域占比橙色区域的面积为1:4,所以通过面积的方式就可以确定概率了。
总结
对于一维情况,可以通过长度值来计算概率
对于二维情况,可以通过面积值来计算概率
对于三维情况,可以通过体积值来计算概率
对于更高维度的情况,可以通过多重积分来计算概率值
