控制建模matlab练习05:比例积分控制-①系统建模
此练习主要是比例积分控制,包括三部分:
①系统建模;
②PI控制器;
③PI控制器的应用;
以下是,第①部分:系统建模。
一、在matlab中建立系统的数学模型
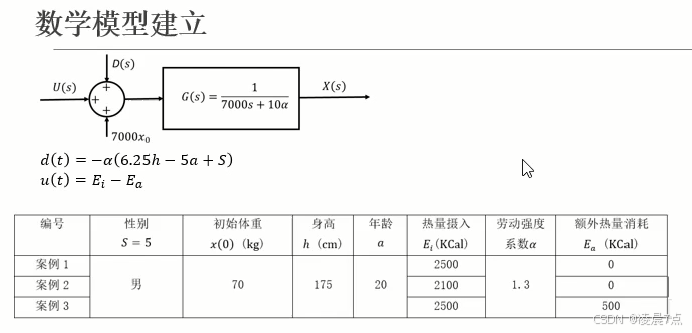
1、这个一个体重系统的数学模型,如下图;
2、同时,举例三个案例,每个案例的具体数值,如表格;
- 传递函数:G(s)
- 输入有三部分:D(s)、U(s)、7000x0
- D(s)是扰动部分,对应的时间函数是下面的d(t)=-α(6.25h-5a+S);
- U(s)是每日净热量摄入,对应的时间函数是下面的u(t)=Ei-Ea;
3、系统的输出
- 从图看出输入为三部分的加和,且是一个线性时不变系统,所以输出=系统对这三个输入分别的响应的加和。
- 因为d(t)和u(t)相当于两个常数,所以系统对常数的响应=系统的单位阶跃响应x这个常数倍。
- 而7000x0是系统的初始条件,所以也就是系统的冲激响应。
clc;clear;close all;
%% 定义参数
S = 5;
x0 = [70];
h = 175;
a = 20;
Ei = [2500,2100,2500];
alpha = 1.3;
Ea = [0, 0, 500];
%% 定义G(s)
G_s = tf([1],[7000,10*alpha]);
%% 定义扰动和输入
d = -alpha*(6.25*h-5*a+S);
u1 = (Ei(1)-Ea(1));
u2 = (Ei(2)-Ea(2));
u3 = (Ei(3)-Ea(3));
%% 系统的输出
% 从图看出输入为三部分的加和,且是一个线性时不变系统,所以输出=系统对这三个输入分别的响应的加和。
% 因为d(t)和u(t)相当于两个常数,所以系统对常数的响应=系统的单位阶跃响应x这个常数倍。
% 而7000x0是系统的初始条件,所以也就是系统的冲激响应。
t = 0: 1: 3000;
x1 = (u1+d)* step(G_s,t) + 7000 * x0 * impulse(G_s,t) ;
x2 = (u2+d)* step(G_s,t) + 7000 * x0 * impulse(G_s,t) ;
x3 = (u3+d)* step(G_s,t) + 7000 * x0 * impulse(G_s,t) ;
%% 绘图
plot (x1, 'b');
hold on
plot (x2, 'k');
hold on
plot (x3, 'r');
grid on;
hold off;
legend ('Case 1', 'Case 2', 'Case 3');二、运行结果与分析
案例1:体重会上升到90多公斤,且有界;
案例2:体重会下降到60多公斤,且有界;
案例3:体重会下降到50多公斤,且有界;
(区别就在于,每天热量摄入以及热量消耗的不同)
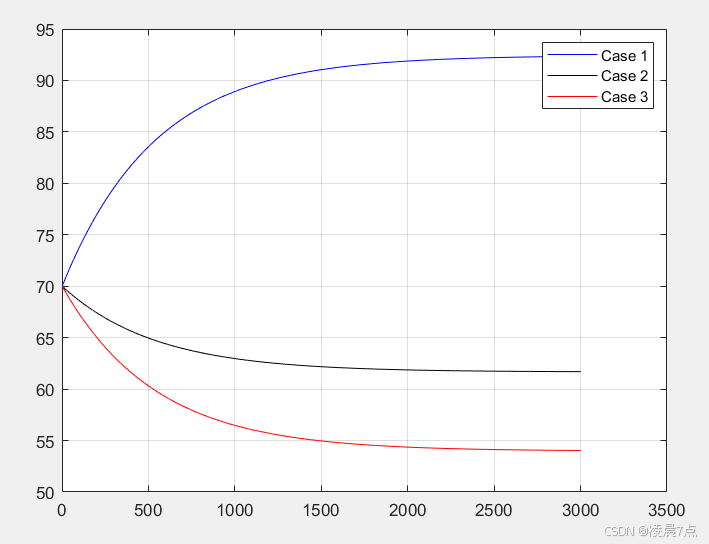
- 可以看出,这三个案例最后都会趋向于稳定值;
- 因为,整个系统不管输入是什么,由系统的传递函数来决定的;
- 此时,检验系统传递函数的极点,在运行之后命令行窗口打pole(G_s);
- 得到传递函数极点是-0.0019,是一个负值,说明是一个稳定的系统;
- 所以,当输入U(s)和D(s)有界的时候,输出一定有界。

学习来源:《控制之美》[卷1],王天威
