当前位置：首页 > news >正文

扩散模型（一）——综述

news 2025/8/4 10:11:30

3月记的笔记拖到草稿箱最下面8月发出来......

前面零散地梳理了几篇笔记，终于到了关键核心部分：扩散模型

首先扩散模型属于基于能量的深度生成模型之一，但因为在具身智能领域过于重要，因此单独记成一类笔记

认真梳理一下全套流程，整个大活

在之前的笔记已经简单梳理了一遍 VAE 和 GAN 这两种生成模型，尽管两者均能生成较为真实的样本，但它们也存在各自的局限性：

GAN 利用对抗训练机制，虽然能够生成高质量的图像，但其训练过程容易出现不稳定性，同时生成样本的多样性往往不足
VAE 则通过对数据似然下界的优化来进行训练，虽然具备一定理论优势，但在实际生成图像时，其图像质量常常不尽如人意

相比之下，扩散模型（Diffusion Models） 作为基于马尔可夫链的生成模型，不仅在图像生成上表现出色，还能生成高质量的图片、视频和音乐。其名字来源于自然界中的扩散现象，就像水中的墨水慢慢散开一样，分子从高浓度区域向低浓度区域转移并逐渐均匀分布

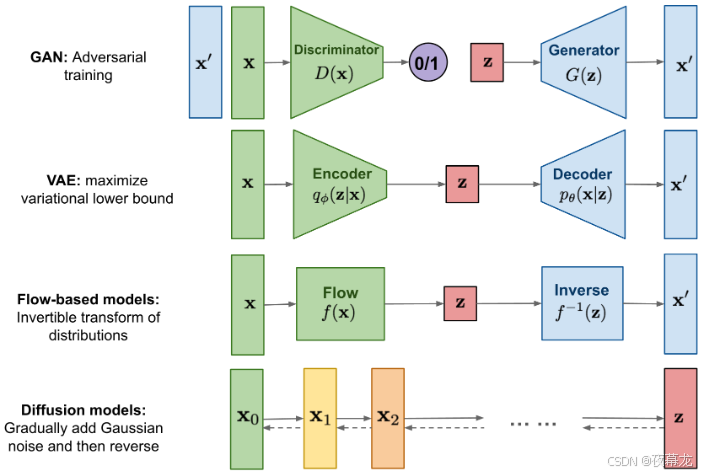
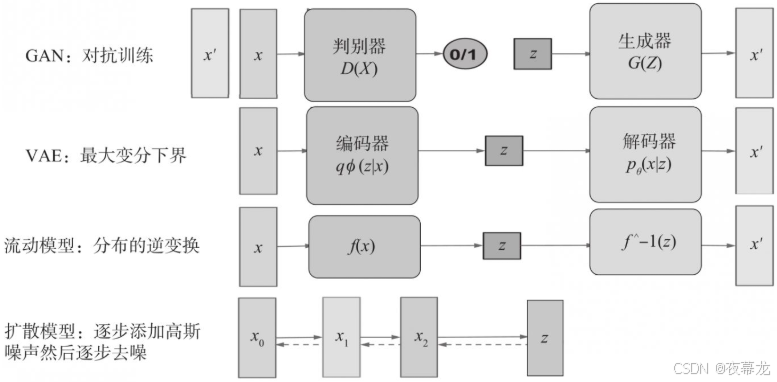
深度生成模型架构对比

扩散模型通过在数据中添加随机噪声，然后逆转这一过程，从噪声中恢复出原始数据分布，从而创造出新的数据。例如，DALL-E 3、Midjourney v6、Sora 等模型，只要简单描述想法，就能生成想要的图片或视频

1 理论基础与设计灵感

2 扩散模型工作原理

2.1 数据预处理

2.2 正向扩散过程

2.3 逆向生成过程

2.4 小结

3 扩散模型架构

3.1 去噪扩散概率模型（DDPMs）

3.2 分数生成模型（SGMs）

3.3 随机微分方程（SDEs）

3.4 对比

4 扩散模型与其他生成模型的对比

4.1 与 GAN 的对比

4.2 与 VAE 的对比

1 发展历史与理论基础

1.1 发展历史

扩散模型是一类基于概率分布的生成式模型，其核心思想是通过逆向扩散过程从噪声数据逐步恢复原始数据分布。其技术发展历程围绕以下关键创新展开：

朗之万动力学（Langevin Dynamics）
作为扩散模型的理论基础，朗之万动力学通过引入随机噪声模拟粒子在势能场中的随机运动，启发了后续扩散过程中噪声驱动的数据生成机制。该方法为物理、化学领域的随机过程建模提供了数学框架
去噪分数匹配（Denoising Score Matching，2010）
Roux等人将朗之万动力学与概率建模结合，提出去噪分数匹配算法。其核心是通过对加噪样本的梯度估计，直接建模数据分布的对数梯度（分数函数），解决了高维数据中分数匹配的难题，为扩散模型奠定了训练框架
扩散过程与逆向推断（2015）
Sohl-Dickstein等人首次将正向扩散过程（逐步向数据添加噪声）与逆向扩散过程（逐步去噪恢复数据）结合，构建完整的生成模型。通过马尔可夫链建模多步噪声扰动，并利用变分推断优化逆向过程的参数，实现了从噪声到数据的可逆生成路径
无参数扩散与流模型融合（2019）
Song等人提出无参数扩散过程，将扩散模型嵌入流模型（Flow-Based Model）框架，通过确定性微分方程描述数据演化路径。这一方法避免了离散化噪声步骤的限制，提升了生成效率与灵活性
深度学习驱动的范式革新（2019至今）
基于深度学习的优化，扩散模型涌现出三大核心范式：
- DDPM（去噪扩散概率模型）：通过加权损失函数优化去噪过程，显著提升生成质量
- SGM（分数生成模型）：结合随机微分方程（SDE）统一扩散与分数匹配，实现连续时间建模
- SDE-Based Diffusion：将生成过程形式化为随机微分方程的解，支持更灵活的噪声调度与采样策略

1.2 理论基础

目前主流的扩散模型由 Sohl-Dickstein et al 等人提出并由 Ho. et al 2020 在2020年进一步发展为去噪扩散概率模型（Denoising Diffusion Probabilistic Models，DDPM），其设计灵感主要来源于非平衡热力学中的扩散现象。具体而言，在非平衡热力学中，系统与环境之间经常发生物质与能量的交换。例如，如果在装有水的容器中滴入一滴墨水，墨水会逐渐在水中扩散，直到均匀分布在整个容器中。如果将这一扩散过程中的每一步都控制得足够小，那么理论上这一过程是可逆的

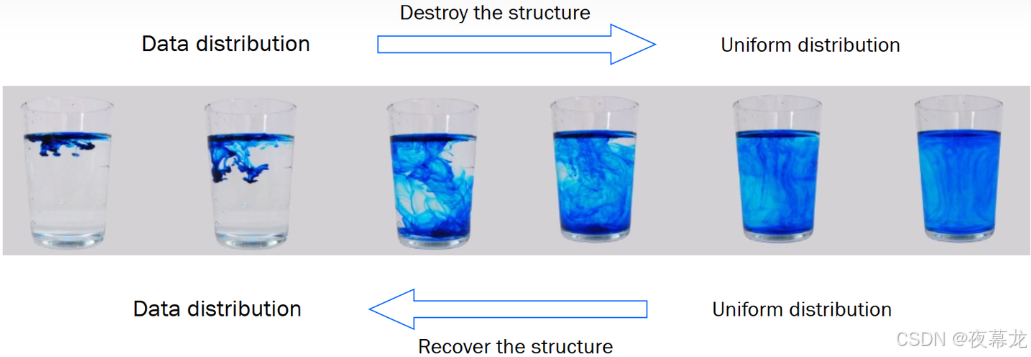
基于这一理论，DDPM 模型主要包括两个阶段：

前向加噪阶段：将原始数据 $\mathbf{x}_0$ 作为起始点，每一步为其添加足够小的高斯噪声，经过足够多的步骤 T，使得 $\mathbf{x}_0$ 最终符合标准高斯分布
反向去噪阶段：试图从噪声数据中恢复出有用的数据。因为前向过程是可行的，所以理论上反向去噪过程也是可行的，这两个过程互为逆操作

这种方法不仅能生成逼真的图像和连贯的文本序列，还在医学图像分析、自动驾驶技术、个人 AI 助手等领域展现出巨大潜力。可以形象地理解为：先给一幅画随意涂抹颜色，再通过细致的擦除与修复，最终恢复出一幅精美的作品

2 扩散模型工作原理

扩散模型的核心思想是通过模拟噪声扩散的过程来逼近目标分布，整个过程可以看作一个由马尔可夫链构成的逐步生成过程

PS：马尔可夫过程的意思就是当前时刻的状态只由上一时刻的状态决定，而不由更早的状态决定。例如：计算 $\mathbf{x}_t$ ，只需要用到 $\mathbf{x}_{t-1}$

2.1 数据预处理

在扩散过程开始之前，需要对数据进行适当的预处理，以便模型能更好地捕捉数据的特征。数据预处理通常包括：

数据清洗：去除异常值
数据标准化：使得不同特征具有一致的尺度
数据增强：增加数据集的多样性，尤其在图像处理中常见

对噪声图像还需进行标准化处理，以确保数据分布的正常性。对于文本、图像等不同类型数据，也可能需要针对性的预处理方法，例如解决类别不平衡的问题

2.2 正向扩散过程 forward process

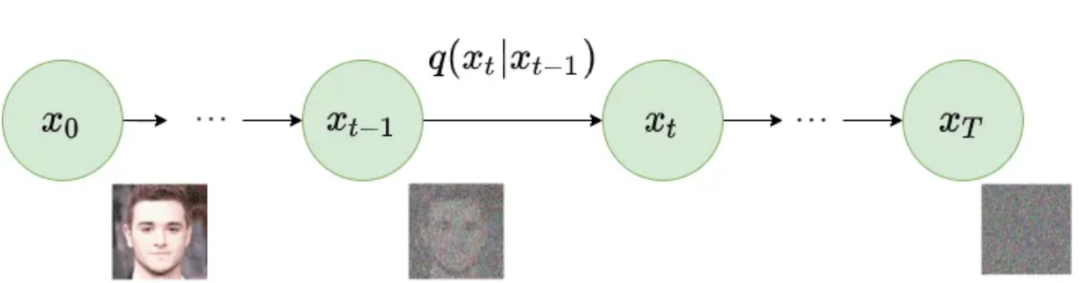
在正向过程（forward process）中，将数据逐步注入噪声，使其最终变为接近简单分布（通常是标准正态分布）的状态。假设初始数据为 $\mathbf{x}_0$ ，正向过程可以定义为一系列条件分布：

$q(\mathbf{x}_t|\mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1-\beta_t}\,\mathbf{x}_{t-1},\, \beta_t \mathbf{I})$

其中：

t = 1,2,…,T 表示扩散的步数
βt 为在第 t 步中添加的噪声方差
N 表示高斯分布，I 是单位矩阵

经过 T 个步骤后，得到的样本近似服从如下分布：

$q(\mathbf{x}_T) \approx \mathcal{N}(\mathbf{x}_T; \mathbf{0}, \mathbf{I})$

直观来说，这个过程就像是在一张白纸上从一个简单的点开始，逐步添加结构化噪声，使其逐渐演变为复杂的数据分布

2.3 逆向生成过程 reverse process

扩散模型的生成过程则为逆向过程（reverse process），其目标是从简单分布（如 $\mathcal{N}(\mathbf{0}, \mathbf{I})$ ）逐步逆转噪声的注入，恢复出原始数据的结构。逆向过程通过参数化的转移概率来实现：

$p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t),\, \Sigma_\theta(\mathbf{x}_t, t))$

其中：

$\mu_\theta(\mathbf{x}_t, t)$ 和 $\Sigma_\theta(\mathbf{x}_t, t)$ 是由神经网络学习得到的均值和协方差
θ 为模型参数，通过最大似然估计或者变分推断等方法进行优化

训练时，模型通常采用变分下界（Variational Lower Bound, VLB）来近似数据对数似然，并通过最大似然估计来优化参数，确保反向过程能有效逆转正向扩散中的噪声添加，最终恢复出数据的原始结构

2.4 小结

扩散模型由正向过程和反向过程这两部分组成，这可以类比于 VAE 中的编码器和解码器

在正向过程中，输入的原始图像会不断混入高斯噪声；经过多次加噪声操作后，图像最终会变成一幅符合标准正态分布的纯噪声图像。而在反向过程中，希望训练出一个神经网络，该网络能够学会相应的去噪声操作，将纯噪声图像还原回原始图像。网络的学习目标是使得每一步的去噪声操作正好能够抵消对应的加噪声操作

训练完毕后，只需要从标准正态分布中随机采样出一个噪声，再利用反向过程中的神经网络将该噪声恢复成一幅图像，就能够生成一幅新图片

3 扩散模型架构

目前，扩散模型主要基于以下三种整体架构：

3.1 去噪扩散概率模型（DDPMs）

核心思想：基于离散时间步的马尔可夫链，通过正向加噪和反向去噪的对称过程建模。

工作原理：

正向过程：将数据逐步添加高斯噪声，直到变为纯噪声。每一步按固定规则（如线性调度）离散化噪声强度
反向过程：训练神经网络（如U-Net）预测每一步的噪声，通过迭代去噪从噪声中恢复数据

特点：

离散化：时间步有限且固定（如1000步），实现简单高效
训练目标：直接最小化预测噪声与真实噪声的误差（均方损失）

典型应用：图像生成（如Stable Diffusion）、音频合成

3.2 分数生成模型（SGMs）

核心思想：通过估计数据分布的梯度（即分数函数），引导生成过程向高概率区域移动

关键概念：

分数（Score）：数据分布对数概率密度的梯度（∇ₓ log p(x)），指向数据密集方向
分数匹配：通过扰动数据（加噪）训练网络估计不同噪声水平下的分数

工作原理：

多噪声尺度：在不同噪声尺度下训练噪声条件评分网络（NCSN）
生成过程：基于朗之万动力学（Langevin Dynamics），沿分数方向迭代修正噪声样本

特点：

连续优化：通过梯度信息直接调整样本，无需显式建模分布
灵活性：可处理复杂分布，但对高维数据可能收敛慢

代表工作：NCSN、SMLD（随机微分方程与朗之万结合）

3.3 随机微分方程（SDEs）

核心思想：将扩散过程建模为连续时间的随机微分方程，统一DDPMs和SGMs框架

数学形式：

正向SDE：描述数据逐渐加噪的连续过程（如d𝑥 = 𝑓(𝑥,𝑡)d𝑡 + 𝑔(𝑡)d𝑤）
反向SDE：通过逆向时间求解生成数据，需计算分数函数调整漂移项

关键贡献：

统一视角：DDPMs和SGMs可视为SDE离散化或特定参数化的特例
灵活求解器：可用数值方法（如Euler-Maruyama）灵活选择步长和噪声调度

特点：

理论完备性：提供连续时间分析工具（如概率流ODE）
计算成本：连续化可能增加求解复杂度，但允许更精细控制生成过程

代表工作：Score SDE、Probability Flow ODE

3.4 对比

维度	DDPMs	SGMs	SDEs
时间建模	离散时间步	多噪声尺度（离散/连续）	连续时间微分方程
核心目标	预测噪声	估计分数（梯度）	统一框架下的扩散过程
数学工具	马尔可夫链	朗之万动力学	随机微分方程
生成过程	迭代去噪	沿梯度方向修正样本	求解反向SDE
优势	实现简单、训练稳定	直接优化概率密度梯度	理论统一、灵活性高
局限	固定调度灵活性低	高维收敛慢	数值求解复杂度较高

4 扩散模型与其他生成模型的对比

4.1 与 GAN 的对比

训练稳定性
GAN 需要协调生成器和判别器的对抗训练，容易出现模式崩溃（Mode Collapse）和训练不稳定的问题；而扩散模型采用逐步去噪的方式，训练过程更稳定
样本多样性
由于从噪声开始逐步恢复信息，扩散模型在样本多样性上具有天然优势；而 GAN 可能因过度拟合判别器而生成多样性不足的样本