机器学习04——初识梯度下降
机器学习
机器学习01——初识机器学习
机器学习02——数据与算法初步
机器学习03——数据与算法初步2
文章目录
- 机器学习
- 前言
- 一、梯度下降
- 1.1 概念
- 1.2 梯度
- 1.3 公式
- 1.4 示例
- 总结
前言
在之前的学习中,我们已经初步了解了什么是损失以及损失函数,并学会了如何利用损失函数求解最优拟合函数。
但最小二乘法求解,首先假设损失函数是这样的,利用方程求解导数为0会得到很多个极值,不能确定唯一解。

其次,其时间复杂度至少是O(n3)O(n^3)O(n3),对于大批量的数据来说,还是太慢了,现在的计算机根本无法承受这种计算量。于是,现在常用到的求最优解的方法是更为简便的梯度下降法。
一、梯度下降
1.1 概念
在机器学习中,梯度表示损失函数对于模型参数的偏导数。具体来说,对于每个可训练参数,梯度告诉我们在当前参数值下,沿着每个参数方向变化时,损失函数的变化率。通过计算损失函数对参数的梯度,梯度下降算法能够根据梯度的信息来调整参数,朝着减少损失的方向更新模型,从而逐步优化模型,使得模型性能更好。

梯度下降法(Gradient Descent)是一个算法,但不是像多元线性回归那样是一个具体做回归任务的算法,而是一个非常通用的优化算法来帮助一些机器学习算法求解出最优解,所谓的通用就是很多机器学习算法都是用梯度下降,甚至深度学习也是用它来求解最优解。
所有优化算法的目的都是期望以最快的速度把模型参数W求解出来,梯度下降法就是一种经典常用的优化算法。
1.2 梯度
这里以一个简单的线性模型y=wxy=wxy=wx为例,我们现在要用梯度下降法确定其最最能拟合下图中数据的权重www。
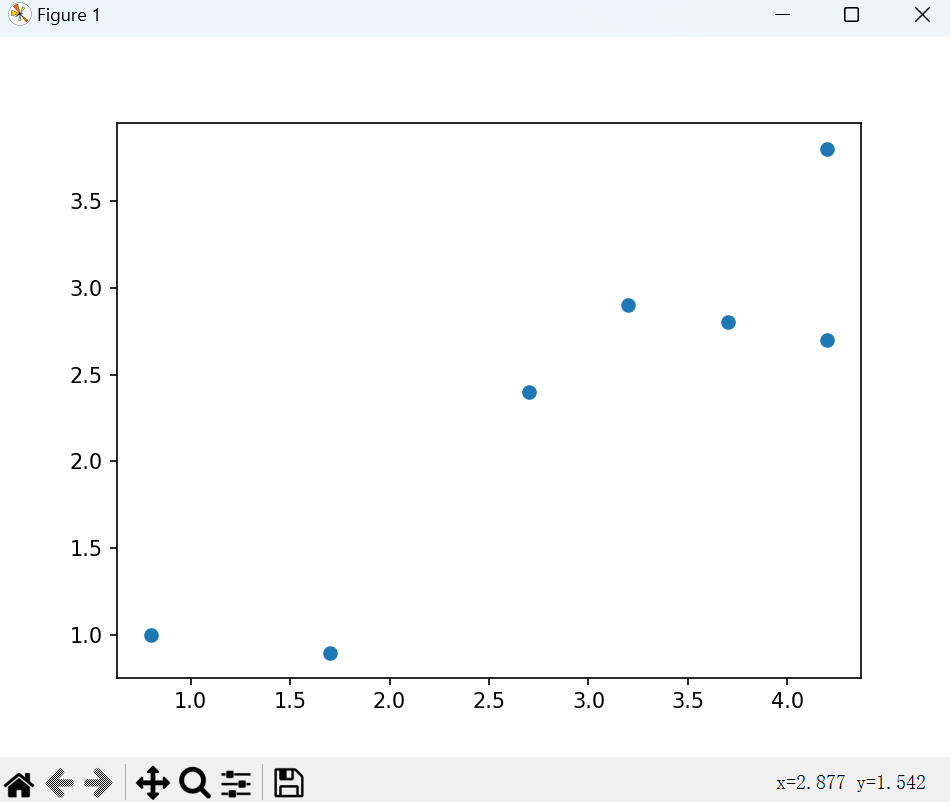
# 数据
points=[4.2, 3.8],[4.2, 2.7],[2.7, 2.4],[0.8, 1.0],[3.7, 2.8],[1.7, 0.9],[3.2, 2.9]
首先我们先随机生成一个权重www,得到如下直线:
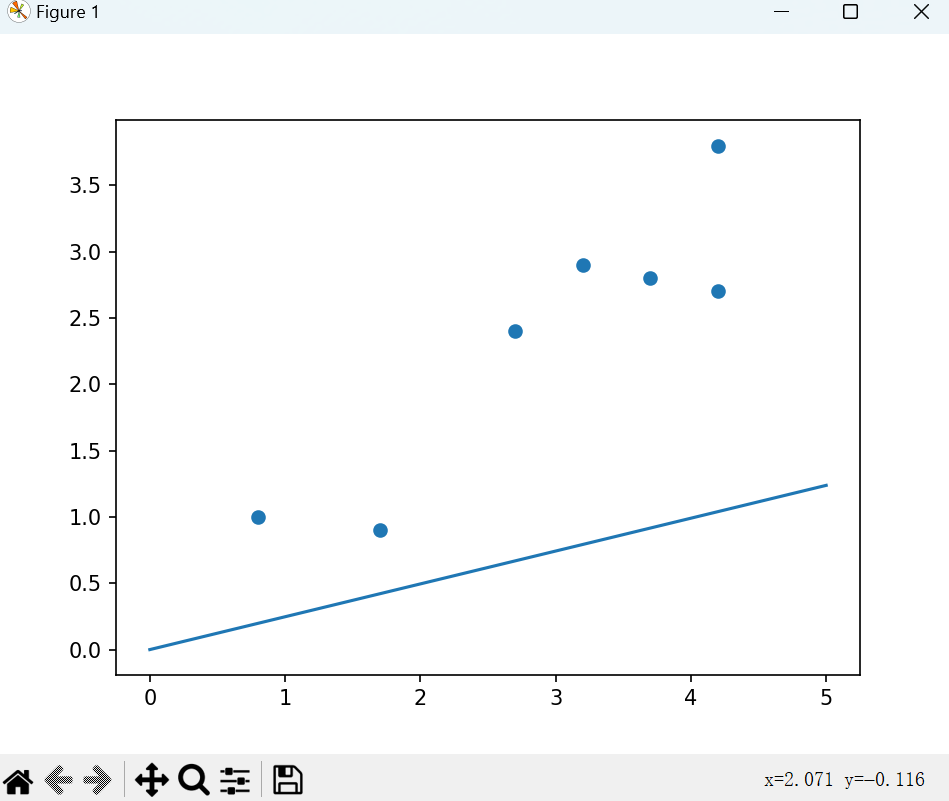
显然这条直线对数据的拟合程度很差。利用我们之前所学习的计算损失的技巧,即可度量这条对象对数据的拟合程度。故接下来,我们要求出损失函数了。
损失函数实质上就是将各个预测值与实际值做差后的值平方后再求和。
loss=(y^1−y1)2+(y^2−y2)2+....(y^n−yn)2loss={(\hat y_1-y_1)^2}+{(\hat y_2-y_2)^2}+....{(\hat y_n-y_n)^2}loss=(y^1−y1)2+(y^2−y2)2+....(y^n−yn)2
变换一下形式,将其变换为关于权重www的函数:
loss=1n∑i=1n(wxi−yi)2=1n∑i=1nxi2w2−2n∑i=1nxiyiw+1n∑i=1nyi2带入以上数据中的各项xi,yi,可得:=aw2+bw+c=10w2−15.9w+6.5\begin{aligned} loss &=\frac{1}{n} \textstyle\sum_{i=1}^{n}(w x_{i}-y_{i})^{2}\\ &={\frac{1}{n}}\sum_{i=1}^{n}x_{i}^{2}w^{2}-{\frac{2}{n}}\sum_{i=1}^{n} x_{i}y_{i}w+{\frac{1}{n}}\sum_{i=1}^{n} y_{i}^{2}\\ &带入以上数据中的各项x_i,y_i,可得:\\ &= {a w^{2}+b w+c} \\ &= 10w^{2}-15.9w+6.5 \end{aligned} loss=n1∑i=1n(wxi−yi)2=n1i=1∑nxi2w2−n2i=1∑nxiyiw+n1i=1∑nyi2带入以上数据中的各项xi,yi,可得:=aw2+bw+c=10w2−15.9w+6.5
这样我们就得到了损失与权重的函数关系。为了得到完美的拟合直线,我们就需要求得当损失losslossloss最小时的权重www。
虽然我们可以通过韦达定理快速求出这个例子中的最佳权重w,但由于韦达定理仅适用于抛物线,而实际情况中,损失函数不一定是抛物线,故我们这里不采用这种方式。
根据高中数学可得,我们可以通过对该函数求导来寻找其极值点,而通常一个函数的极值点很有可能就是其极大值(极小值)点。
求导后可得:
loss′=20w−15.9loss'=20w - 15.9 loss′=20w−15.9
这个导数就是大名鼎鼎的梯度。如果损失函数是个多元函数,那么其梯度就是其各个变量的偏导数所组成的向量。
而当函数取得极值点时,其所对应导数(也可称梯度)为0。也就是说,我们只需要将0代入然后解方程就可以。别急,这种方式虽然在这个例子中非常便捷,但实际情况中,损失函数及其梯度可比这个复杂得多,即使是计算机也很难进行求解。
1.3 公式
接下来这就到了梯度下降法的核心内容了,即根据损失函数的梯度不断调整权重,直到梯度几乎不再变换,我们就认为其收敛了,也就是找到目标解了。
那么我们应该如何根据梯度调整权重呢?
- 一种做法是当梯度不为0或大于某个阈值时,就将权重增加或减少固定值:
如果 ∣∂loss∂w∣>ϵ则 wn+1=wn±δ(符号取决于梯度方向)\text{如果 } \left| \frac{\partial loss}{\partial w} \right| > \epsilon \text{ 则 } w^{n+1} = w^{n} \pm \delta \quad \text{(符号取决于梯度方向)} 如果 ∂w∂loss>ϵ 则 wn+1=wn±δ(符号取决于梯度方向)
缺点:这种方法过于粗糙。它忽略了梯度本身的大小信息。在平缓区域(梯度小),固定步长可能导致更新缓慢;在陡峭区域(梯度大),固定步长又可能跨度过大,导致震荡甚至发散,难以稳定高效地收敛。
- 还有一种做法是直接将权重与减去当前所对应的梯度:
wn+1=wn−δw^{n+1} = w^{n} - \delta wn+1=wn−δ
缺点:这种方法通常会导致步长过大。梯度本身的值可能非常大(尤其是在初始化阶段或遇到陡峭峡谷时),直接减去梯度会使权重发生剧烈的跳跃,同样容易引起震荡,甚至越过最小值点或导致数值不稳定(溢出),几乎不可能收敛到最小值点。
为了解决上述两种方法的缺陷,标准梯度下降法引入了一个至关重要的超参数——学习率(Learning Rate),通常记作 α\alphaα 或 η\etaη。学习率是一个小的正数(例如 0.1, 0.01, 0.001 等),它控制着每次更新步长的大小。
将以上思想抽象为数学公式,则有:

一般情况下学习率在整体迭代过程中是不变,但是也可以设置成随着迭代次数增多学习率逐渐变小,因为越靠近极值点我们就可以步子迈小点,可以更精准的走入最低点,同时防止走过。还有一些深度学习的优化算法会自己控制调整学习率这个值。
1.4 示例
这里参照上面的例子给出一份示例代码:
import numpy as np
import matplotlib.pyplot as pltclass MyModel:def __init__(self,w):self.w=wdef compute(self,x):return self.w*xdef compute_all(self,x):return [self.compute(i) for i in x]# 数据
points=[4.2, 3.8],[4.2, 2.7],[2.7, 2.4],[0.8, 1.0],[3.7, 2.8],[1.7, 0.9],[3.2, 2.9]
x=[i[0] for i in points]
y=[i[1] for i in points]# 绘制数据
plt.scatter(x,y)# 模型绘制
def draw(model):x_range=np.linspace(0,5,100)plt.plot(x_range,model.compute_all(x_range))# 随机生成w
w=np.random.rand()
model=MyModel(w)
draw(model)# 求得损失函数
class MYLoss:def __init__(self,model,x,y):# 第一个系数为x的平方均值,第二个系数为X*y的均,第三个系数为y的平方均值self.a=np.mean([i**2 for i in x])self.b=-2*np.mean([i*j for i,j in zip(x,y)])self.c=np.mean([j**2 for j in y])def get_loss(self,model):return self.a*(model.w**2)+self.b*model.w+self.cdef get_gradient(self,model):return 2*self.a*model.w+self.bloss=MYLoss(model,x,y)
learn_rate=0.5
max_iter=20
for i in range(max_iter):a=learn_rate/(learn_rate+i)model.w=model.w-a*loss.get_gradient(model)print("第%d次迭代,损失为:%f,梯度为:%f,模型权重为:%f"%(i+1,loss.get_loss(model),loss.get_gradient(model),model.w))draw(model)
plt.show()
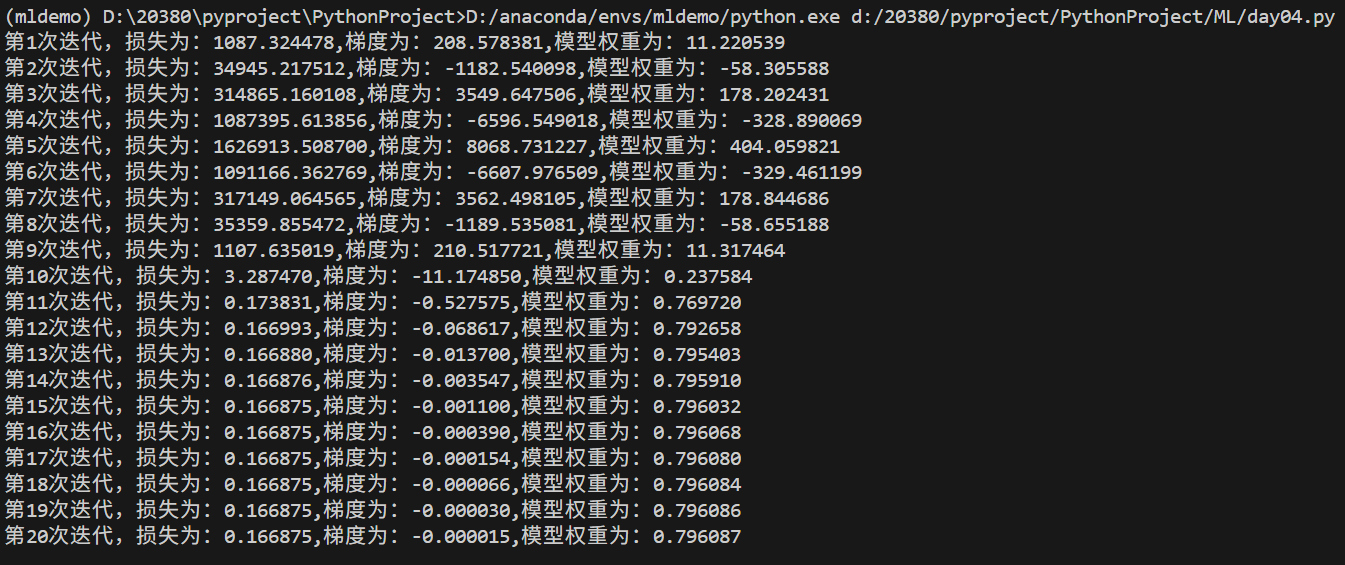
总结
本文简单讲解了梯度下降的概念,并以一个一元线性函数为例简单叙述梯度下降的核心步骤与思想,关于多参数的梯度下降后面的文章会又提到,但读者也可自行探究。
