人工智能概念之十一：常见的激活函数与参数初始化

在神经网络的训练中，激活函数决定了信号的传递方式，而参数初始化则决定了网络的“起点”。两者看似独立，却共同影响着模型的收敛速度与最终性能。今天，我们不仅会解析常见的激活函数（包括近年来流行的GELU等），还会探讨如何根据激活函数选择合适的参数初始化方法，让神经网络“赢在起跑线”。

---

相关文章

人工智能概念之九：深度学习概述：网页链接
人工智能概念之十：人工神经网络（ANN）：网页链接

---

一、激活函数：给网络注入非线性活力

激活函数的核心作用是打破线性映射的局限，让神经网络能够拟合复杂的非线性关系。没有激活函数，再多的网络层也只是“花架子”，无法处理图像、文本等现实世界数据。

假设我们要拟合一个简单的非线性关系：$y=x^2$（比如“面积与边长的平方关系”）。如果不用激活函数，即使堆叠多层神经网络，每一层的输出都是输入的线性组合（如$z=w\cdot x+b$）。例如，第一层输出$z_1=w_{1}x+b_1$，第二层输出$z_2=w_2{z}_1+b_2=w_2(w_{1}x+b_1)+b_2=(w_2{w}_1)x+(w_2{b}_1+b_2)$，本质仍是$y=kx+c$的线性形式，无论多少层都无法表达$x^2$这样的曲线关系。

但加入激活函数后（如ReLU：$f(z)=\max (0,z)$），情况完全不同。假设第一层计算$z_1=w_{1}x+b_1$，经ReLU激活后得到$a_1=\max (0,z_1)$；第二层用$z_2=w_2{a}_1+b_2$，再通过激活函数输出。通过调整权重，网络可以组合出类似“$x>0$时输出$x^2$，$x<0$时输出$x^2$”的非线性映射，最终精准拟合$y=x^2$。这就是激活函数的核心价值：为网络注入非线性“能力”，让深层结构真正拥有拟合复杂现实关系的潜力。

1.1 经典激活函数：奠定神经网络基础

1.1.1 Sigmoid函数：早期的“概率开关”

Sigmoid函数的公式为：
$$\sigma (x)=\frac{1}{1+e^{-x}}$$

• 特性：将输入映射到(0, 1)区间，适合作为二分类任务的输出层（如判断“垃圾邮件/正常邮件”）。
• 缺陷：
  • 输入绝对值较大时（|x| > 6），梯度接近0，易导致深层网络“梯度消失”。
  • 输出均值为0.5（非零中心），会导致梯度更新方向单一，影响训练效率。
    

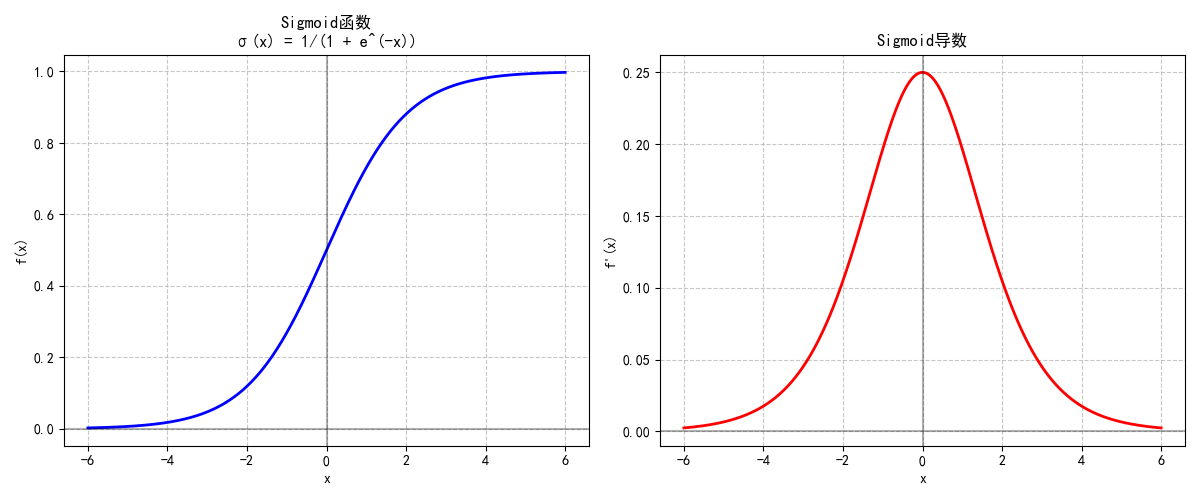
1.1.2 Tanh函数：零中心的“改进版Sigmoid”

Tanh（双曲正切函数）公式为：
$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

• 特性：输出范围为(-1, 1)，以0为中心，梯度更新效率优于Sigmoid。
• 缺陷：输入绝对值较大时（|x| > 3），梯度仍会趋近于0，深层网络仍可能梯度消失。
  

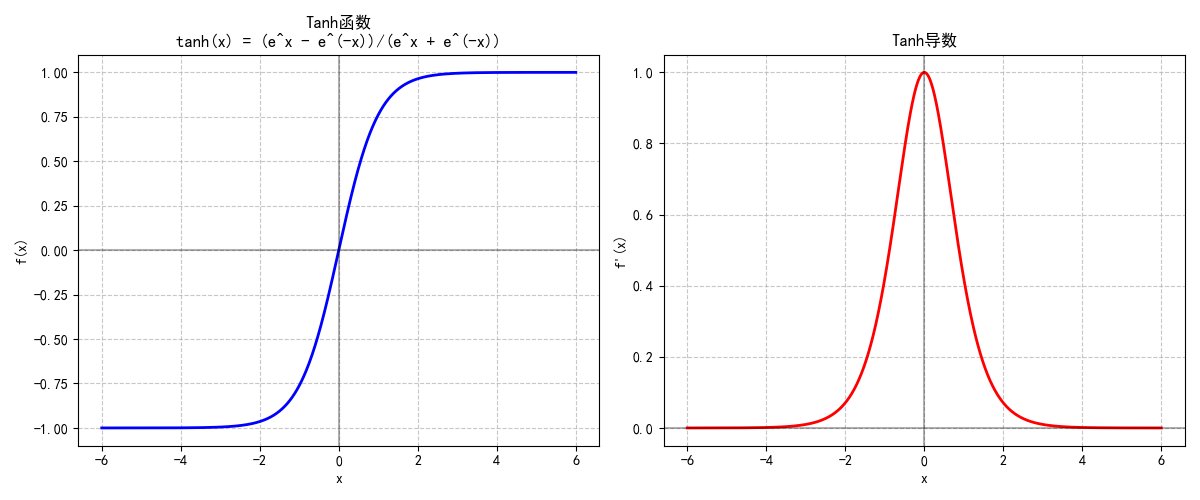
1.1.3 ReLU函数：当代神经网络的“主力选手”

ReLU（修正线性单元）公式极简：
$$\text{ReLU}(x)=\max (0,x)$$

• 特性：
  • 输入为正时直接输出原值（梯度为1），避免梯度消失，适合深层网络。
  • 计算高效（无需指数运算），稀疏激活（负输入输出0），缓解过拟合。
• 缺陷：存在“神经元死亡”问题（输入长期为负时，神经元永久失效），可通过Leaky ReLU（负输入保留小斜率）缓解。
  

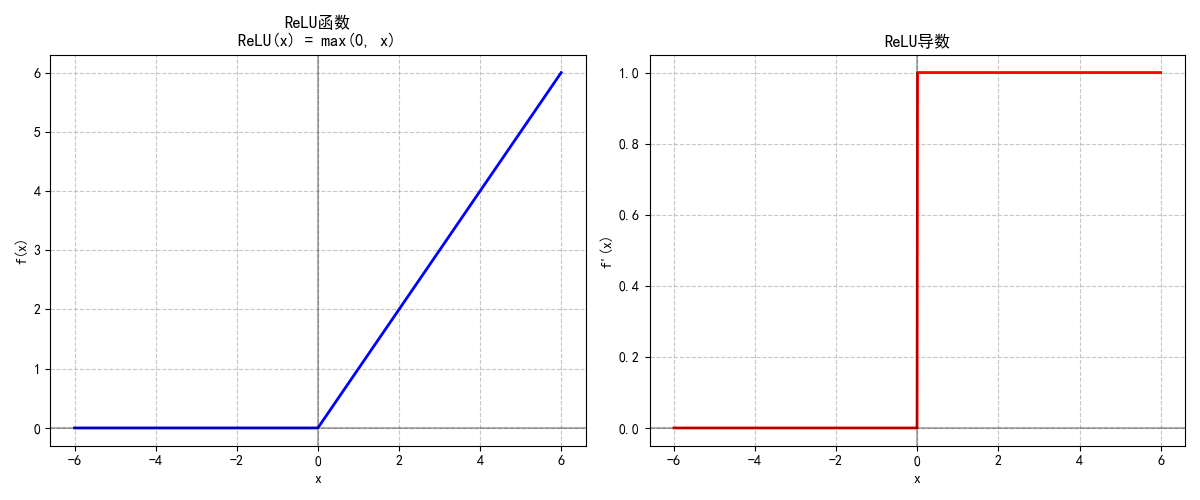
1.1.4 Softmax函数：多分类的“概率分配器”

Softmax专为多分类设计，公式为：
$$\text{Softmax}(z_i)=\frac{e^{z_i}}{{\sum }_{j=1}^k{e}^{z_j}}$$

• 特性：将输入转换为和为1的概率分布，直接输出每个类别的预测概率（如“猫/狗/鸟”的分类）。
  

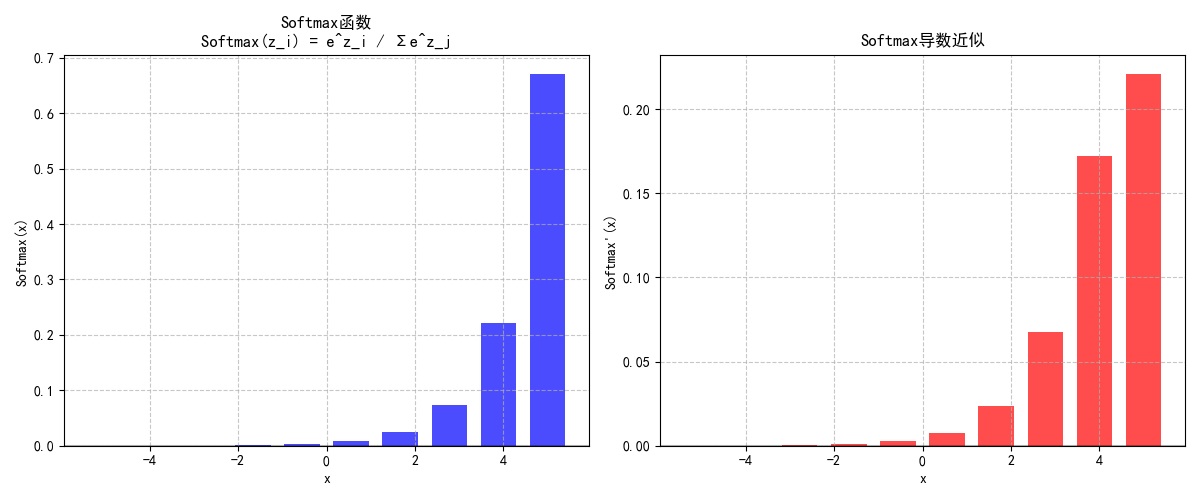
1.2 现代激活函数：为复杂模型而生

1.2.1 GELU (Gaussian Error Linear Unit)

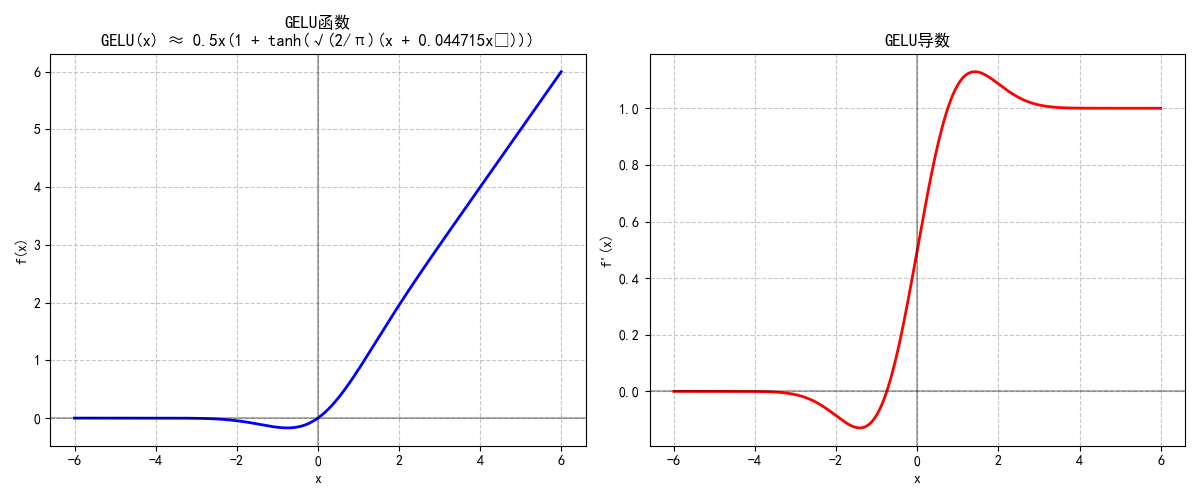
GELU是近年来Transformer架构的“标配”，公式近似为：
$$\text{GELU}(x)\approx 0.5x\left(1+\tanh \left(\sqrt{\frac{2}{\pi }}\left(x-0.044715x^3\right)\right)\right)$$

• 特性：
  • 结合ReLU的非线性与正态分布的随机正则化效果，输出随输入概率性激活。
  • 平滑连续、处处可导，彻底避免“死亡神经元”问题。
  • 在BERT、GPT等大语言模型中表现远超ReLU，成为自然语言处理任务的首选。
    

1.2.2 Swish/SiLU (Sigmoid-weighted Linear Unit)

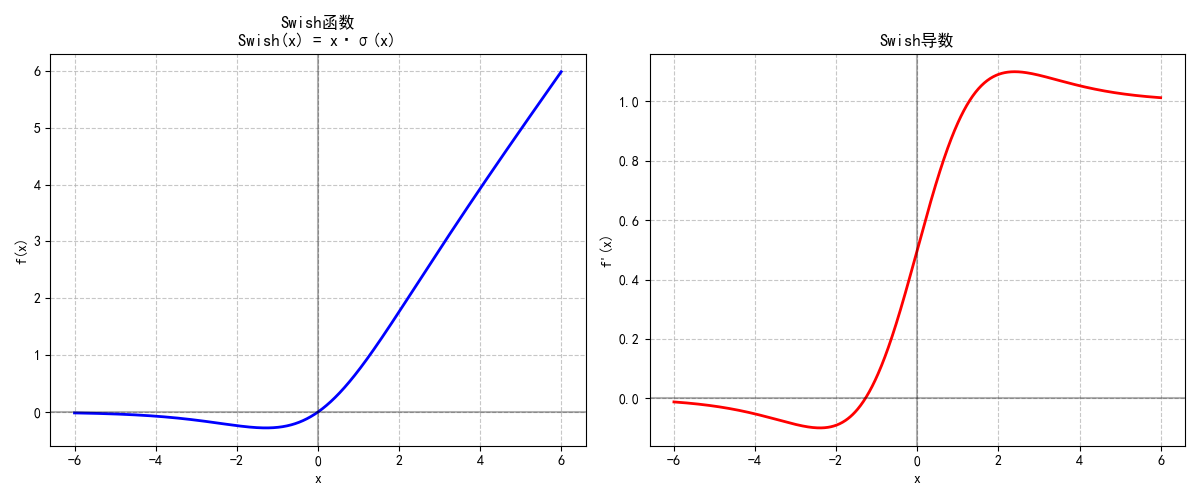
Swish由Google提出，是带自门控机制的激活函数：
$$\text{Swish}(x)=x\cdot \sigma (x)$$
（其中$\sigma$为Sigmoid函数）

• 特性：
  • 非单调特性让它能更好地捕捉复杂模式，在深层网络中性能优于ReLU。
  • 计算简单（仅比ReLU多一次Sigmoid运算），梯度流动稳定。
  • PyTorch中F.silu(x)与$\beta =1$的Swish完全等价：$\text{SiLU}(x)=x\cdot \sigma (x)=\text{Swish}(x)$，已成为计算机视觉任务的常用选择。
    

1.2.3 Mish

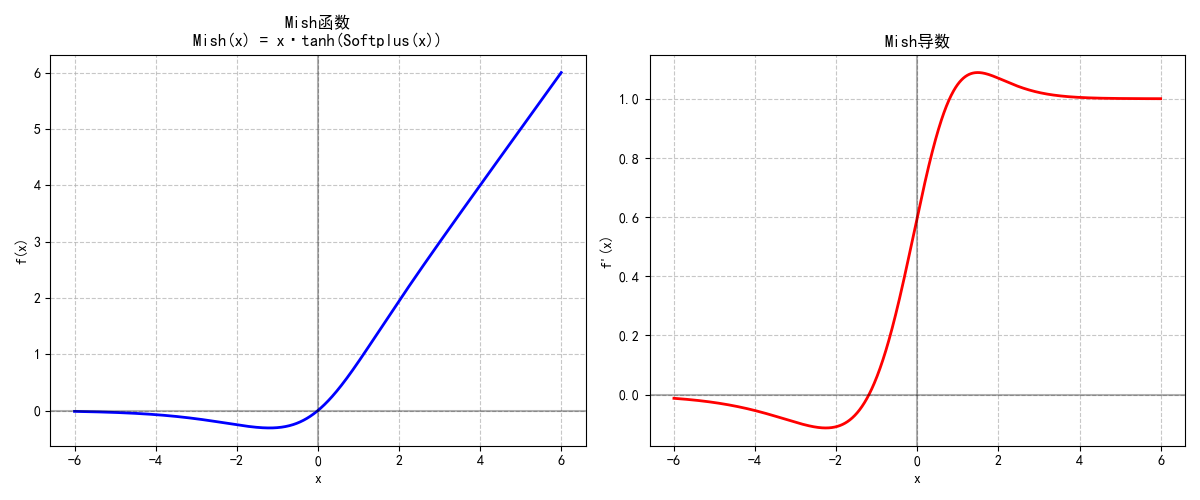
Mish结合了Tanh和Softplus的优点，公式为：
$$\text{Mish}(x)=x\cdot \tanh (\text{Softplus}(x))$$
（其中$\text{Softplus}(x)=\log (1+e^x)$）

• 特性：
  • 无上界（避免梯度饱和）、有下界（让负值区域更稳定），梯度流动更顺畅。
  • 在目标检测、图像分类等任务中，常能超越Swish和ReLU，但计算成本略高。
    

1.2.4 ELU (Exponential Linear Unit)

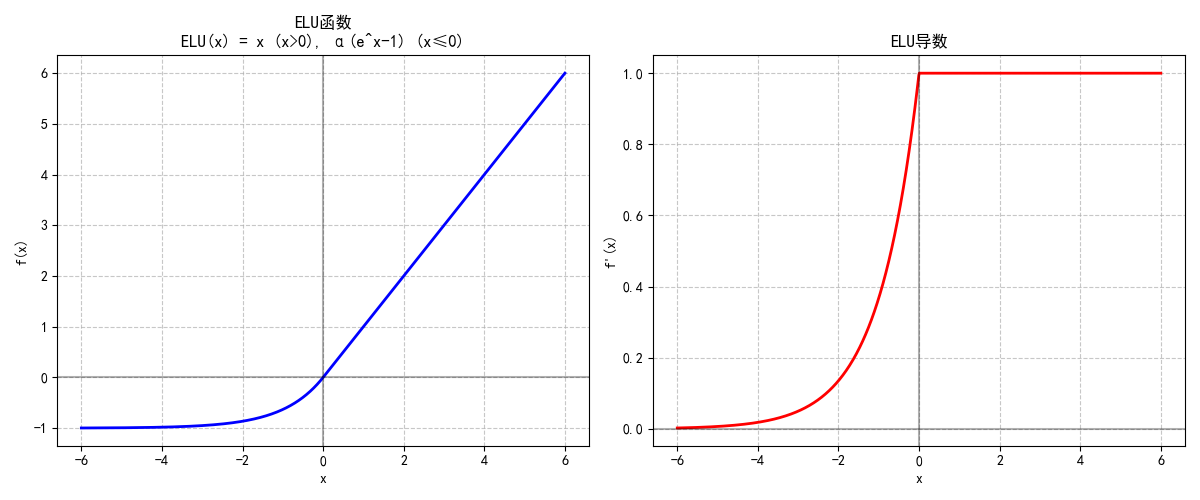
ELU是ReLU的改进版，针对负输入设计：
$$\text{ELU}(x)=\{\begin{array}{ll}x& \text{if }x>0\\ \alpha (e^x-1)& \text{if }x\le 0\end{array}$$

• 特性：
  • 负输入区域通过指数函数平滑过渡，输出均值接近0，加速收敛。
  • 减少“死亡神经元”问题，但指数运算增加了计算量，实际使用中不如Leaky ReLU普及。
    

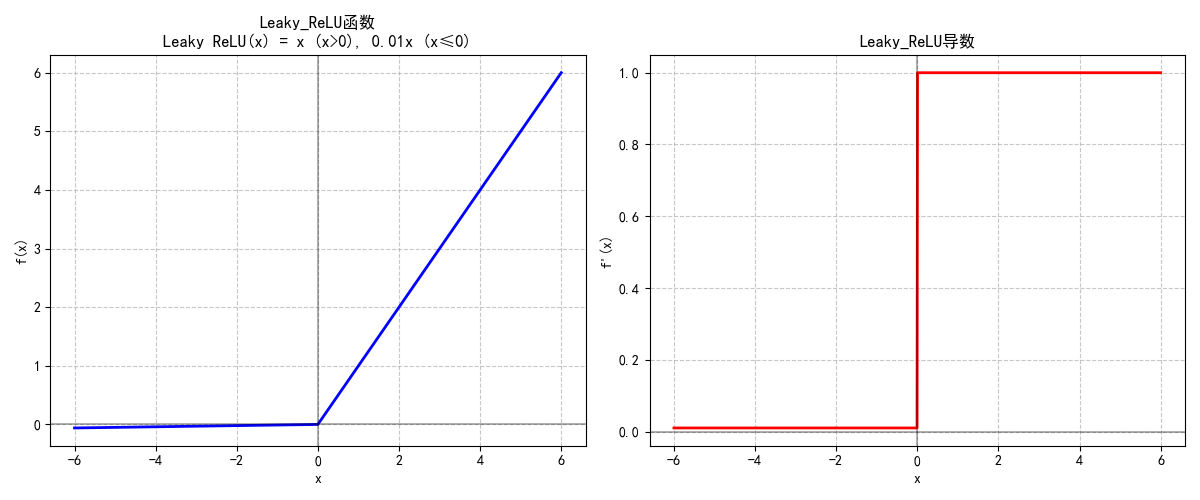
1.2.5 Leaky ReLU与PReLU

两者均为解决ReLU“神经元死亡”问题而设计：

• Leaky ReLU：负输入区域保留固定小斜率（如0.01）：
  $$\text{Leaky ReLU}(x)=\{\begin{array}{ll}x& \text{if }x>0\\ 0.01x& \text{if }x\le 0\end{array}$$
• PReLU：负斜率为可学习参数，让模型自适应数据分布，适合数据量充足的场景。
  

1.2.6 SELU (Scaled Exponential Linear Unit)

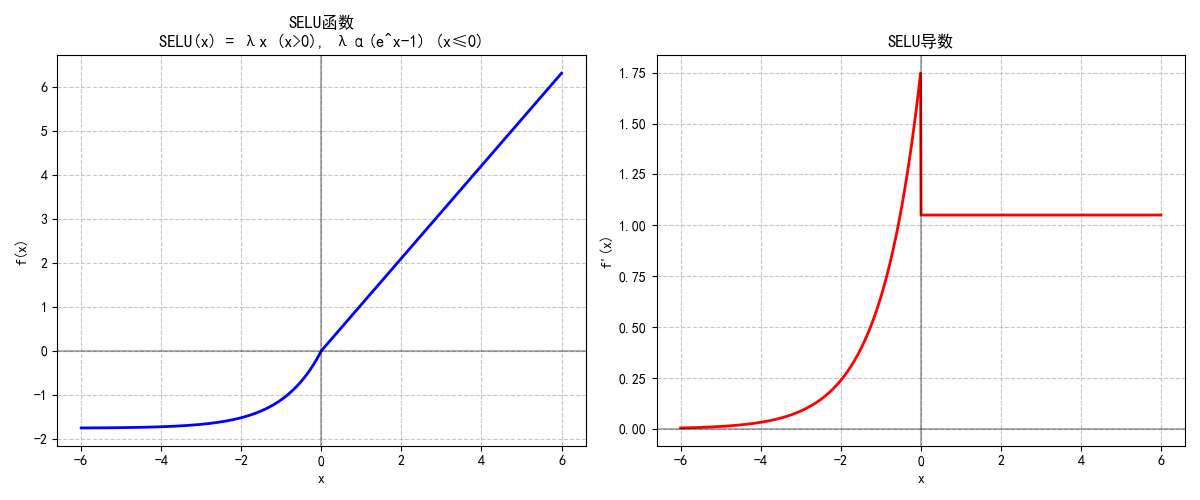
SELU是专为自归一化网络设计的激活函数：
$$\text{SELU}(x)=\lambda \{\begin{array}{ll}x& \text{if }x>0\\ \alpha (e^x-1)& \text{if }x\le 0\end{array}$$
（其中$\alpha \approx 1.6733$, $\lambda \approx 1.0507$ 为固定缩放参数）

• 特性：配合特定初始化（如LeCun初始化），可让网络层输出自动保持均值0、方差1，无需批量归一化。
• 局限：仅适用于特定网络结构（如全连接网络），灵活性较低。
  

---

二、参数初始化：激活函数的“最佳拍档”

神经网络的参数（权重和偏置）初始化直接影响训练效果。不合适的初始化会导致梯度爆炸、收敛缓慢，甚至模型无法训练。初始化方法的选择需与激活函数匹配，才能发挥最佳效果。

2.1 为什么初始化很重要？

• 避免梯度消失/爆炸：权重过大导致激活值急剧膨胀（梯度爆炸），过小则导致信号衰减（梯度消失）。
• 打破对称性：若所有权重初始化为相同值，神经元会学习到相同特征，网络失去表达能力。
• 加速收敛：合理的初始化让激活值分布更稳定，梯度更新更高效。

2.2 常见初始化方法及适用场景

初始化方法	核心思想	适用激活函数	公式（简化）
随机正态/均匀初始化	从正态/均匀分布中随机采样	浅层网络（<5层）	均匀分布：$W\sim U(-a,a)$（a为小值）
Xavier（Glorot）初始化	平衡输入输出方差，避免信号衰减	Sigmoid、Tanh	均匀分布：$W\sim U\left(-\sqrt{\frac{6}{n_{\text{in}}+n_{\text{out}}}},\sqrt{\frac{6}{n_{\text{in}}+n_{\text{out}}}}\right)$
Kaiming（He）初始化	针对ReLU特性，放大输入方差	ReLU、Leaky ReLU、Swish	正态分布：$W\sim N\left(0,\sqrt{\frac{2}{n_{\text{in}}}}\right)$（注：$\sqrt{\frac{2}{n_{\text{in}}}}$ 表示标准差）
LeCun初始化	为SELU设计，控制输出方差为1	SELU	正态分布：$W\sim N\left(0,\frac{1}{n_{\text{in}}}\right)$（注：此处为方差，标准差为$\sqrt{\frac{1}{n_{\text{in}}}}$）
全0/全1初始化	权重全部为0或1	几乎不适用	——

2.3 初始化与激活函数的匹配逻辑

• Sigmoid/Tanh：选择Xavier初始化。这类激活函数在输入接近0时梯度最大，Xavier通过平衡输入输出方差，避免信号在多层传递后衰减。
• ReLU/Leaky ReLU/Swish：选择Kaiming初始化。ReLU会“过滤”一半的负输入，导致输出方差减半，Kaiming通过放大初始化方差（$\sqrt{\frac{2}{n_{\text{in}}}}$）来补偿。
• SELU：必须搭配LeCun初始化，才能实现“自归一化”特性，无需额外归一化层。
• GELU/Mish：实践中常用Kaiming初始化（因与ReLU特性接近），在Transformer中已成为默认选择。

---

三、总结：激活函数与初始化的“黄金法则”

以下是各激活函数的对比表格，涵盖优缺点、适用场景及典型模型应用：

激活函数	优点	缺点	适用场景	典型模型应用
Sigmoid	输出范围(0,1)，可直接作为概率；实现简单	梯度易消失；输出非零中心；计算成本高（指数运算）	二分类输出层	早期神经网络（如MLP）、逻辑回归输出层
Tanh	输出范围(-1,1)，零中心；梯度绝对值大于Sigmoid，收敛更快	梯度易消失；计算成本高（指数运算）	早期RNN隐藏层、自编码器	LSTM（早期版本）、传统自编码器
ReLU	计算高效（无指数运算）；梯度不衰减（x>0时）；稀疏激活缓解过拟合	存在“神经元死亡”问题；输出非零中心	通用隐藏层（CNN、MLP等）	ResNet、VGG、AlexNet等主流CNN模型
Leaky ReLU	解决ReLU的“神经元死亡”问题；计算效率接近ReLU	负斜率为超参数，需手动调整	ReLU效果不佳时的替代方案	目标检测模型（如YOLOv3）、部分CNN变体
PReLU	负斜率可学习，自适应数据分布；性能优于固定斜率的Leaky ReLU	增加模型参数；数据量不足时易过拟合	数据充足的计算机视觉任务	ResNet（部分改进版）、图像分割模型
GELU	平滑连续可导；结合随机性与非线性，适合深层网络；无神经元死亡问题	计算成本略高于ReLU	Transformer架构、大语言模型	BERT、GPT系列、T5等预训练语言模型
Swish/SiLU	非单调特性捕捉复杂模式；梯度流动稳定；性能优于ReLU	计算成本略高于ReLU（含Sigmoid运算）	计算机视觉、深层CNN	MobileNetV3、EfficientNet、Vision Transformer（ViT）
Mish	无上界避免梯度饱和；有下界稳定负值区域；梯度流动更顺畅	计算成本较高（含Tanh和Softplus）	高精度视觉任务	YOLOv4、YOLOv5、部分目标检测与图像分类模型
ELU	负输入区域平滑过渡；输出均值接近0，加速收敛	计算成本高（指数运算）；性能提升有限	需避免神经元死亡的场景	少量自编码器、强化学习模型
SELU	自归一化特性，无需批量归一化；适合深层网络	仅适用于特定网络结构（如全连接）；对初始化敏感	自归一化神经网络（SNN）	自归一化全连接网络、部分强化学习策略网络
Softmax	输出和为1，直接作为多分类概率；易于解释	计算成本高（指数运算）；对异常值敏感	多分类输出层	所有多分类模型（如ResNet分类头、BERT文本分类输出层）

说明：  
1. 表格中“计算成本”以ReLU为基准（设为1），Sigmoid/Tanh约为2-3，GELU/Swish约为1.5，Mish/ELU约为3-4。  
2. “典型模型应用”为该激活函数表现突出的场景，实际中可能存在交叉使用（如Swish也可用于NLP模型）。  
3. 现代模型（如Transformer、CNN）优先选择GELU/Swish/ReLU，传统模型或特定场景（如二分类）仍保留Sigmoid/Softmax。

1. 激活函数选对“类型”：

   • 通用场景：ReLU（简单高效）或Leaky ReLU（避免神经元死亡）。
   • Transformer/大语言模型：GELU（平滑稳定，适配注意力机制）。
   • 计算机视觉：Swish/SiLU（非单调特性捕捉图像细节）。
   • 输出层：二分类用Sigmoid，多分类用Softmax，回归用线性输出。

2. 初始化找对“搭档”：

   • Sigmoid/Tanh配Xavier，ReLU/Swish/GELU配Kaiming，SELU配LeCun——这是经过实践验证的“最优组合”。
   • 偏置通常初始化为0（无需复杂策略）。

3. 灵活调试：若模型收敛慢或梯度异常，可尝试更换初始化方法（如从正态分布换为均匀分布），或在小范围内调整激活函数的超参数（如Leaky ReLU的负斜率）。

激活函数与参数初始化就像神经网络的“引擎”和“燃料”，只有匹配得当，才能让模型高效运转。理解它们的特性与关联，是构建高性能神经网络的基础。

---

四、绘图代码

# 导入numpy库，用于数值计算
import numpy as np
# 导入matplotlib.pyplot库，用于绘图
import matplotlib.pyplot as plt
# 从math库中导入pi和sqrt函数
from math import pi, sqrt# 设置matplotlib的全局参数
# 设置字体为SimHei（黑体），支持中文显示
plt.rcParams["font.family"] = ["SimHei"]
# 设置axes.unicode_minus为False，解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题# 定义激活函数及其导数# Sigmoid激活函数：将输入映射到(0,1)区间
def sigmoid(x):# 使用sigmoid函数公式：1/(1+e^(-x))return 1 / (1 + np.exp(-x))# Sigmoid函数的导数
def sigmoid_derivative(x):# 先计算sigmoid值s = sigmoid(x)# sigmoid导数公式：s*(1-s)return s * (1 - s)# Tanh（双曲正切）激活函数：将输入映射到(-1,1)区间
def tanh(x):# 使用tanh函数公式：(e^x - e^(-x))/(e^x + e^(-x))return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))# Tanh函数的导数
def tanh_derivative(x):# tanh导数公式：1-tanh^2(x)return 1 - np.square(tanh(x))# ReLU（修正线性单元）激活函数：返回输入和0的最大值
def relu(x):# 使用numpy的maximum函数，返回x和0的最大值return np.maximum(0, x)# ReLU函数的导数
def relu_derivative(x):# 当x>0时导数为1，否则为0return np.where(x > 0, 1, 0)# Softmax激活函数：将输入转换为概率分布
def softmax(x):# 为避免数值溢出，减去最大值（数值稳定性技巧）exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))# 返回归一化的概率分布return exp_x / np.sum(exp_x, axis=-1, keepdims=True)# Softmax函数的导数（近似）
def softmax_derivative(x):# 将输入reshape为1行多列的矩阵s = softmax(x.reshape(1, -1))# softmax导数近似计算：s*(1-s)return s * (1 - s)# GELU（高斯误差线性单元）激活函数
def gelu(x):# GELU函数的近似计算公式return 0.5 * x * (1 + tanh(sqrt(2/pi) * (x + 0.044715 * np.power(x, 3))))# GELU函数的导数
def gelu_derivative(x):# GELU导数的近似计算# 计算tanh项tanh_term = tanh(sqrt(2/pi) * (x + 0.044715 * np.power(x, 3)))# 返回GELU导数计算结果return 0.5 * (1 + tanh_term) + 0.5 * x * (1 - np.square(tanh_term)) * sqrt(2/pi) * (1 + 3 * 0.044715 * np.square(x))# Swish激活函数（也称为SiLU）
def swish(x):# Swish函数公式：x * sigmoid(x)return x * sigmoid(x)# Swish函数的导数
def swish_derivative(x):# 先计算sigmoid值s = sigmoid(x)# Swish导数公式：s + x*s*(1-s)return s + x * s * (1 - s)# Mish激活函数
def mish(x):# Mish函数公式：x * tanh(softplus(x))，其中softplus(x)=log(1+e^x)return x * tanh(np.log(1 + np.exp(x)))# Mish函数的导数
def mish_derivative(x):# 计算softplus值softplus = np.log(1 + np.exp(x))# 计算tanh(softplus)tanh_softplus = tanh(softplus)# 返回Mish导数计算结果return tanh_softplus + x * (1 - np.square(tanh_softplus)) * (np.exp(x) / (1 + np.exp(x)))# ELU（指数线性单元）激活函数
def elu(x, alpha=1.0):# 当x>0时返回x，否则返回alpha*(e^x-1)return np.where(x > 0, x, alpha * (np.exp(x) - 1))# ELU函数的导数
def elu_derivative(x, alpha=1.0):# 当x>0时导数为1，否则为alpha*e^xreturn np.where(x > 0, 1, alpha * np.exp(x))# Leaky ReLU激活函数
def leaky_relu(x, alpha=0.01):# 当x>0时返回x，否则返回alpha*xreturn np.where(x > 0, x, alpha * x)# Leaky ReLU函数的导数
def leaky_relu_derivative(x, alpha=0.01):# 当x>0时导数为1，否则为alphareturn np.where(x > 0, 1, alpha)# SELU（自归一化指数线性单元）激活函数
def selu(x, lambda_=1.0507, alpha=1.67326):# SELU函数：lambda_ * (x if x>0 else alpha*(e^x-1))return lambda_ * np.where(x > 0, x, alpha * (np.exp(x) - 1))# SELU函数的导数
def selu_derivative(x, lambda_=1.0507, alpha=1.67326):# SELU导数：lambda_ * (1 if x>0 else alpha*e^x)return lambda_ * np.where(x > 0, 1, alpha * np.exp(x))# 单独绘制每个激活函数的图像
def plot_single_activation(func, deriv, name, formula, x_range=(-6, 6)):# 生成x值：在指定范围内生成1000个均匀分布的点x = np.linspace(x_range[0], x_range[1], 1000)# 计算函数值和导数值# 计算激活函数在x上的值y = func(x)# 计算导数函数在x上的值dy = deriv(x)# 创建两个子图（函数和导数）：1行2列的子图布局fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))# 绘制函数图像# 使用蓝色实线绘制函数图像ax1.plot(x, y, 'b-', linewidth=2)# 设置第一个子图的标题，包含函数名和公式ax1.set_title(f'{name}函数\n{formula}')# 添加网格线，设置为虚线样式，透明度0.7ax1.grid(True, linestyle='--', alpha=0.7)# 添加水平轴线（y=0）ax1.axhline(y=0, color='k', linestyle='-', alpha=0.3)# 添加垂直轴线（x=0）ax1.axvline(x=0, color='k', linestyle='-', alpha=0.3)# 设置x轴标签ax1.set_xlabel('x')# 设置y轴标签ax1.set_ylabel('f(x)')# 绘制导数图像# 使用红色实线绘制导数图像ax2.plot(x, dy, 'r-', linewidth=2)# 设置第二个子图的标题，显示函数名和"导数"ax2.set_title(f'{name}导数')# 添加网格线，设置为虚线样式，透明度0.7ax2.grid(True, linestyle='--', alpha=0.7)# 添加水平轴线（y=0）ax2.axhline(y=0, color='k', linestyle='-', alpha=0.3)# 添加垂直轴线（x=0）ax2.axvline(x=0, color='k', linestyle='-', alpha=0.3)# 设置x轴标签ax2.set_xlabel('x')# 设置y轴标签ax2.set_ylabel("f'(x)")# 调整子图布局，使子图之间不重叠plt.tight_layout()# 保存图像到文件（注释掉的代码）# plt.savefig(f'{name}_activation.png', dpi=300, bbox_inches='tight')# 显示图像plt.show()# 单独绘制Softmax函数
def plot_softmax():# 为softmax单独处理（因为它通常用于多分类）# 生成softmax的x值：在-5到5之间生成10个点x_softmax = np.linspace(-5, 5, 10)# 计算softmax函数值softmax_values = softmax(x_softmax)# 计算softmax导数值softmax_deriv_values = softmax_derivative(x_softmax)# 创建画布：1行2列的子图布局fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))# 绘制Softmax函数# 使用蓝色柱状图绘制softmax函数值ax1.bar(x_softmax, softmax_values.flatten(), color='b', alpha=0.7)# 设置第一个子图的标题ax1.set_title('Softmax函数\nSoftmax(z_i) = e^z_i / Σe^z_j')# 添加网格线ax1.grid(True, linestyle='--', alpha=0.7)# 添加水平轴线ax1.axhline(y=0, color='k', linestyle='-', alpha=0.3)# 设置x轴标签ax1.set_xlabel('x')# 设置y轴标签ax1.set_ylabel('Softmax(x)')# 绘制Softmax导数# 使用红色柱状图绘制softmax导数值ax2.bar(x_softmax, softmax_deriv_values.flatten(), color='r', alpha=0.7)# 设置第二个子图的标题ax2.set_title('Softmax导数近似')# 添加网格线ax2.grid(True, linestyle='--', alpha=0.7)# 添加水平轴线ax2.axhline(y=0, color='k', linestyle='-', alpha=0.3)# 设置x轴标签ax2.set_xlabel('x')# 设置y轴标签ax2.set_ylabel("Softmax'(x)")# 调整子图布局plt.tight_layout()# 保存图像到文件（注释掉的代码）# plt.savefig('Softmax_activation.png', dpi=300, bbox_inches='tight')# 显示图像plt.show()# 创建绘图函数
def plot_all_activations_separately():# 生成x值：在-6到6之间生成1000个均匀分布的点x = np.linspace(-6, 6, 1000)# 定义激活函数列表：包含函数、导数、名称和公式activation_functions = [# Sigmoid函数及其导数、名称和公式(sigmoid, sigmoid_derivative, "Sigmoid", "σ(x) = 1/(1 + e^(-x))"),# Tanh函数及其导数、名称和公式(tanh, tanh_derivative, "Tanh", "tanh(x) = (e^x - e^(-x))/(e^x + e^(-x))"),# ReLU函数及其导数、名称和公式(relu, relu_derivative, "ReLU", "ReLU(x) = max(0, x)"),# GELU函数及其导数、名称和公式(gelu, gelu_derivative, "GELU", "GELU(x) ≈ 0.5x(1 + tanh(√(2/π)(x + 0.044715x³)))"),# Swish函数及其导数、名称和公式(swish, swish_derivative, "Swish", "Swish(x) = x·σ(x)"),# Mish函数及其导数、名称和公式(mish, mish_derivative, "Mish", "Mish(x) = x·tanh(Softplus(x))"),# ELU函数及其导数、名称和公式（使用lambda表达式包装）(lambda x: elu(x), lambda x: elu_derivative(x), "ELU", "ELU(x) = x (x>0), α(e^x-1) (x≤0)"),# Leaky ReLU函数及其导数、名称和公式（使用lambda表达式包装）(lambda x: leaky_relu(x), lambda x: leaky_relu_derivative(x), "Leaky_ReLU", "Leaky ReLU(x) = x (x>0), 0.01x (x≤0)"),# SELU函数及其导数、名称和公式（使用lambda表达式包装）(lambda x: selu(x), lambda x: selu_derivative(x), "SELU", "SELU(x) = λx (x>0), λα(e^x-1) (x≤0)")]# 绘制每个激活函数及其导数（单独图像）# 遍历所有激活函数并绘制for func, deriv, name, formula in activation_functions:plot_single_activation(func, deriv, name, formula)# 单独绘制Softmax函数plot_softmax()# 程序入口点：当脚本直接运行时执行
if __name__ == '__main__':# 调用绘图函数，绘制所有激活函数plot_all_activations_separately()