解密数据结构之二叉树
前言:各位老铁好,今天笔者给各位老铁分享一下有关二叉树的知识,相信各位老铁对树应该不陌生了,在现实中,我们到处都可以看到树,那么在计算机中也有像树一下的结构,称为树。

下面笔者就给各位老铁讲解一下计算机中树的概念吧。
1.树的概念
树是一种非线性的数据结构,它是由n(n>=0)个结点组成具有层次关系的集合。
之所以把它叫做树,是因为它的结构就像一个倒挂起来的树。
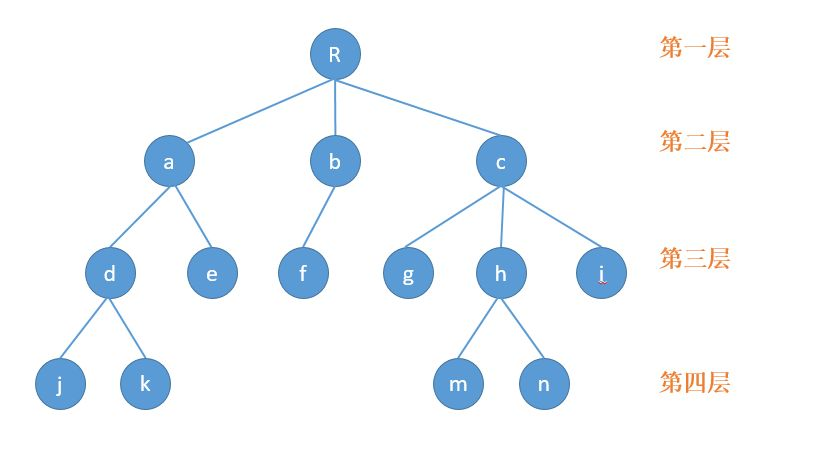
2.树相关的概念
(1)根结点:最上层的结点叫做根结点(根结点是没有前驱的)
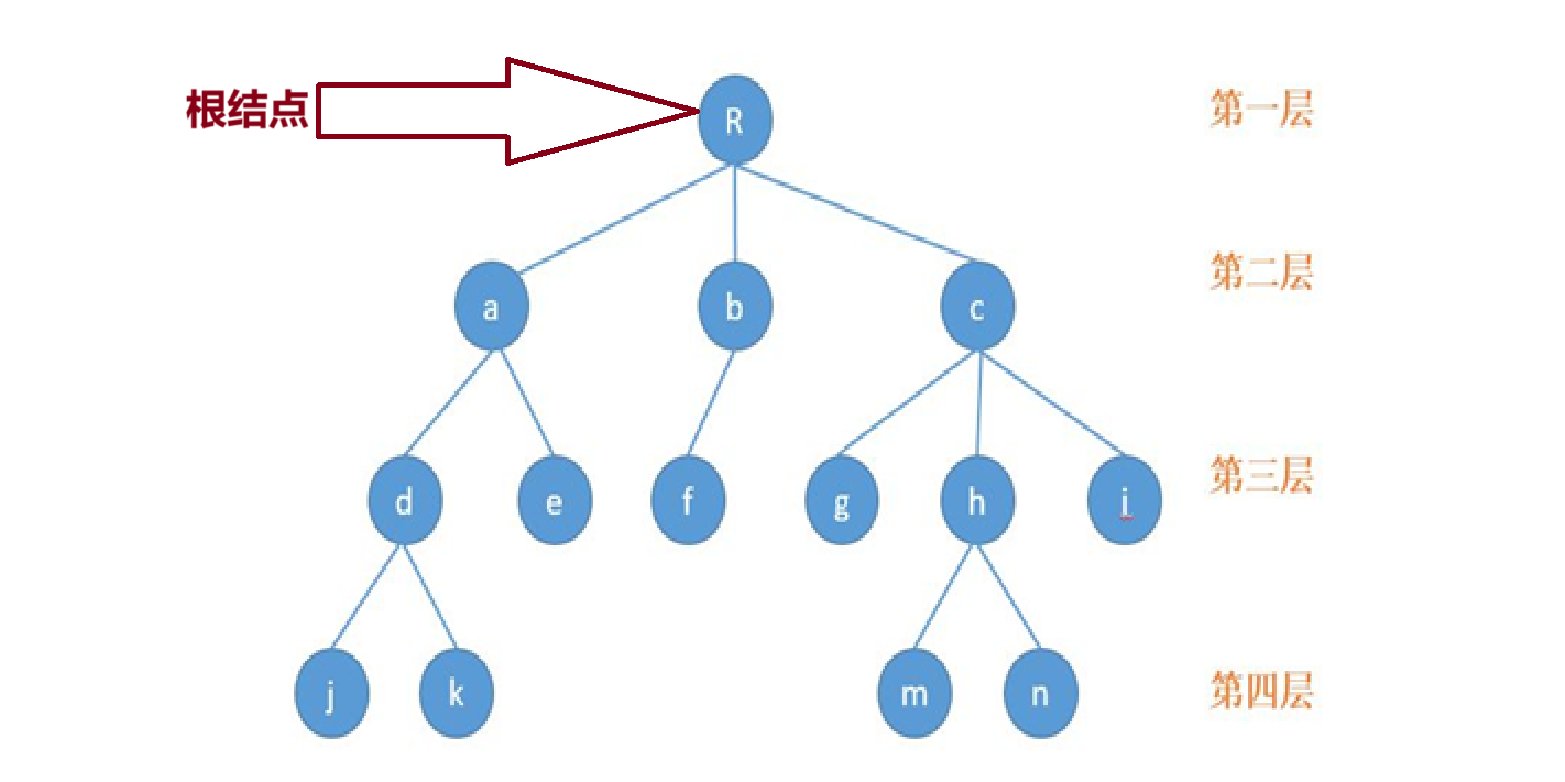
(2)节点的度:一个节点含有子树的个数
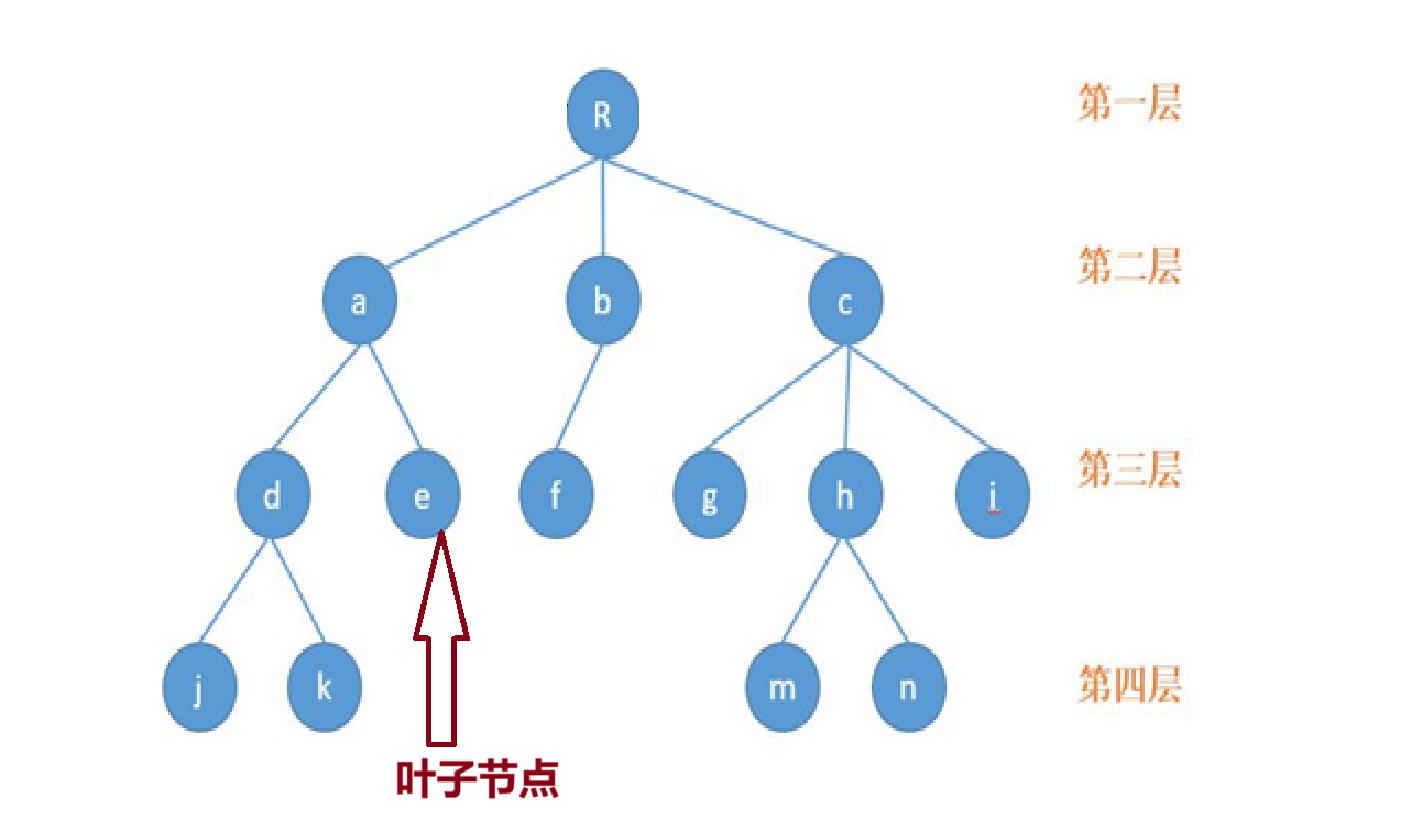
(3)叶子节点:度为0的节点
(4)父节点:若一个节点含有子节点,那么这个节点是它子节点的父节点
(5)兄弟节点:具有相同父节点的节点
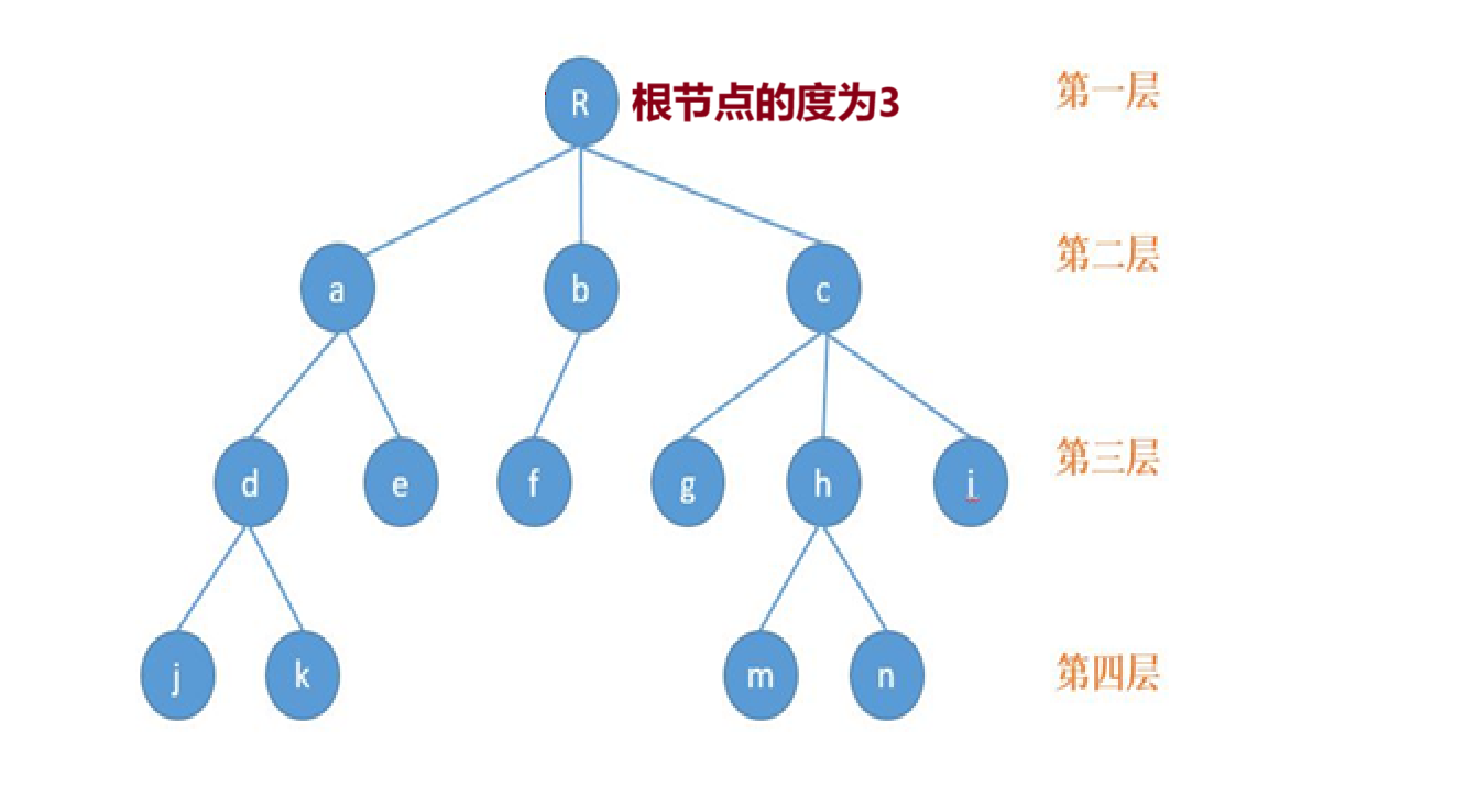
(6)树的度:最大的节点的度
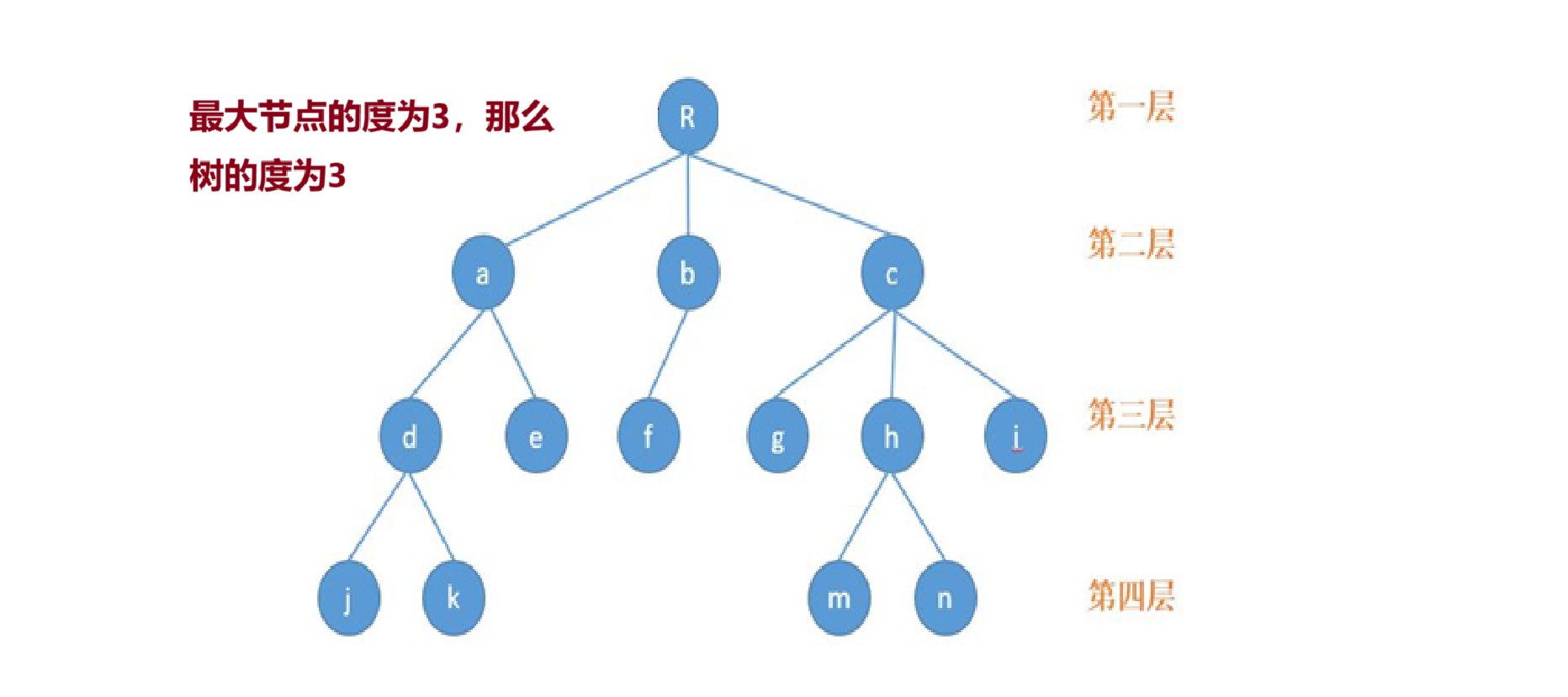
(7)树的高度(树的深度):树的节点的最大层数
(8)森林:由m(m>0)棵互不相交的树组成的集合
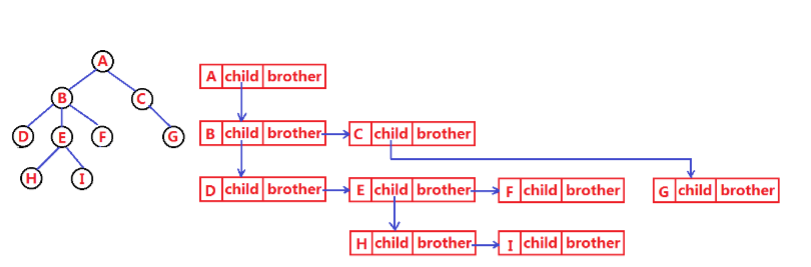
3.树的表示(这里使用孩子兄弟表示法)
树的结构是比较复杂的,那么我们要把它存储起来就比较麻烦,既要保存节点的值,也要保存节点和节点之间的关系。
struct Node
{int _data;//节点的值Node* _firstChild;//指向最左边的孩子Node* _pNextBrother;//指向当前节点的孩子节点的下一个兄弟节点
};
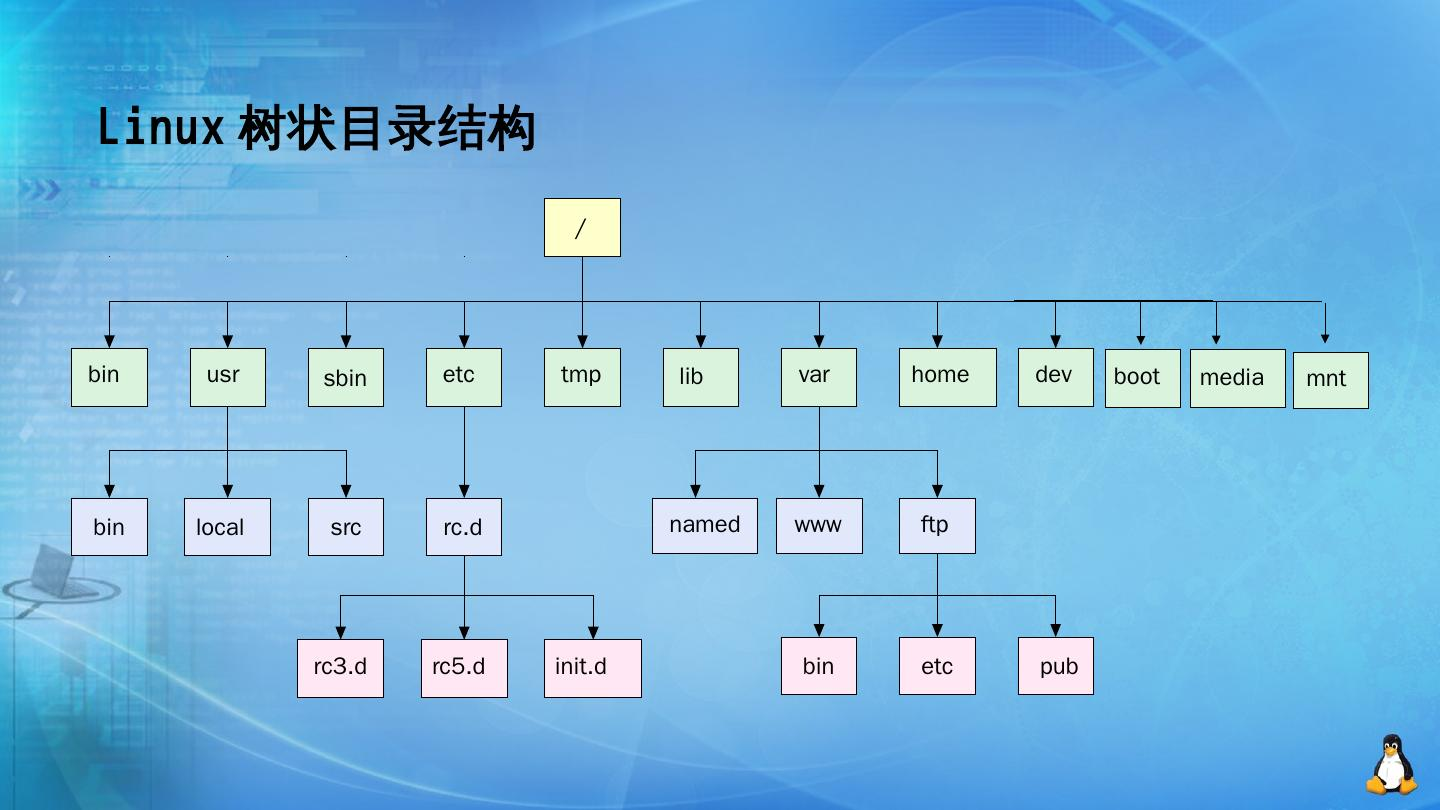
4.树在实际中的运用
Linux的目录结构
5.二叉树概念
再讲二叉树之前,我们先来看看现实中的二叉树

而计算机中的二叉树就是把现实中的二叉树倒过来看就行了。
从图中我们就可以看出,二叉树是由一个根节点和一个左节点和一个右节点构成,所以我们可以得出二叉树的度绝对不超过2,二叉树是有左右之分,所以二叉树是有序树
6.特殊的二叉树
(1)满二叉树:二叉树的每一层节点都达到最大值(假设有k层,那么它总共有2^k-1个节点)
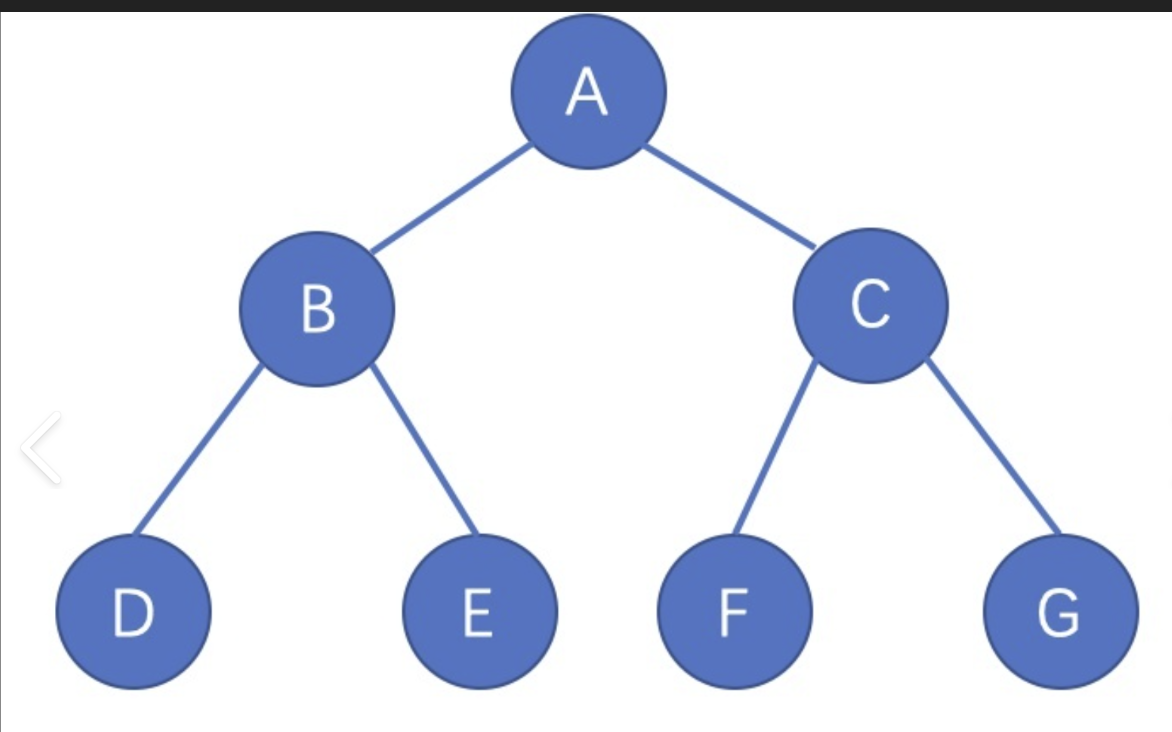
(2)完全二叉树:完全二叉树是一种特殊的二叉树,它的每一层(除了最后一层)都被填满,在最后一层必须尽可能向左排列
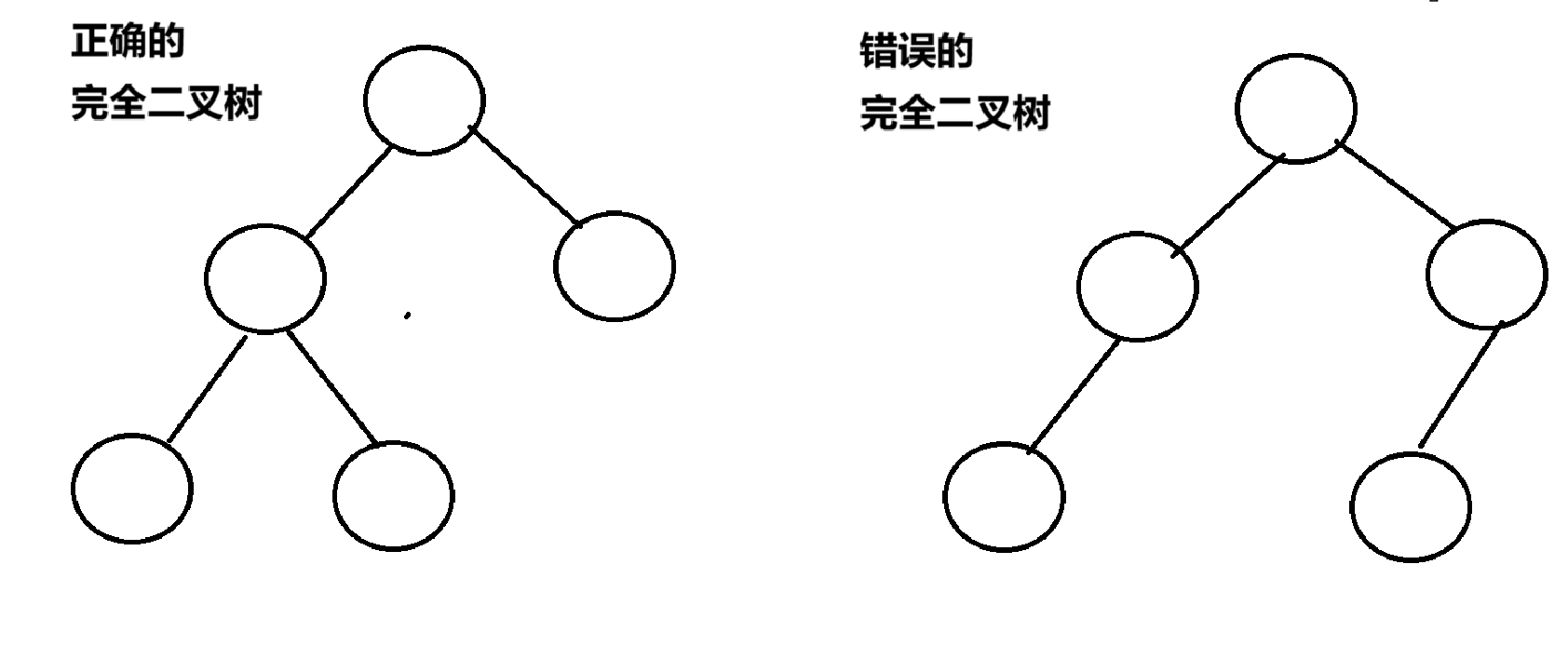
7.二叉树的性质
(1)若二叉树的根节点的层数为1,那么第i层上最多有2^(i-1)个节点
(2)若二叉树的根节点层数为1,那么深度为h的二叉树的总节点个数为2^h-1
(3)对于二叉树,如果度为0的节点个数为n0,度为2的节点个数为n2,那么n0=n2+1
(4)具有n个节点的满二叉树,那么它的深度h=log2(n+1)
8.二叉树的存储结构
(1)顺序结构:顺序结构存储二叉树就是使用数组来存储二叉树,只有是完全二叉树才能使用数组来存储,在后面笔者会为大家讲解堆,而堆底层就是完全二叉树。
(2)链式结构:链式存储二叉树是指使用链表来存储二叉树,链式结构有二叉链结构,也有三叉链结构,什么是二叉链结构,什么又是三叉链结构呢?
二叉链是每一个节点都有两条链指向自己的左右孩子节点
三叉链:三叉链是指不仅有两条链指向自己左右孩子节点,还有一条链指向自己的父节点。
下面笔者给大家使用代码来定义二叉链和三叉链结构
//二叉链
struct BinaryTreeNode1
{int _data;//当前节点的值BinaryTreeNode1* _left;//指向当前节点的左孩子BinaryTreeNode1* _right;//指向当前节点的右孩子
};//三叉链
struct BinnaryTreeNode2
{int _data;//当前节点的值BinnaryTreeNode2* _parent;//指向当前节点的父节点BinnaryTreeNode2* _left;//指向当前节点的左孩子BinnaryTreeNode2* _right;//指向当前节点的右孩子
};
9.二叉树的遍历
由于二叉树的构建需要用到二叉树遍历的知识,所以笔者把二叉树构建放到后面,笔者先来给各位老铁讲解二叉树的各中遍历方式。
(1)二叉树的前序遍历:规则是先根,再左子树,最后右子树
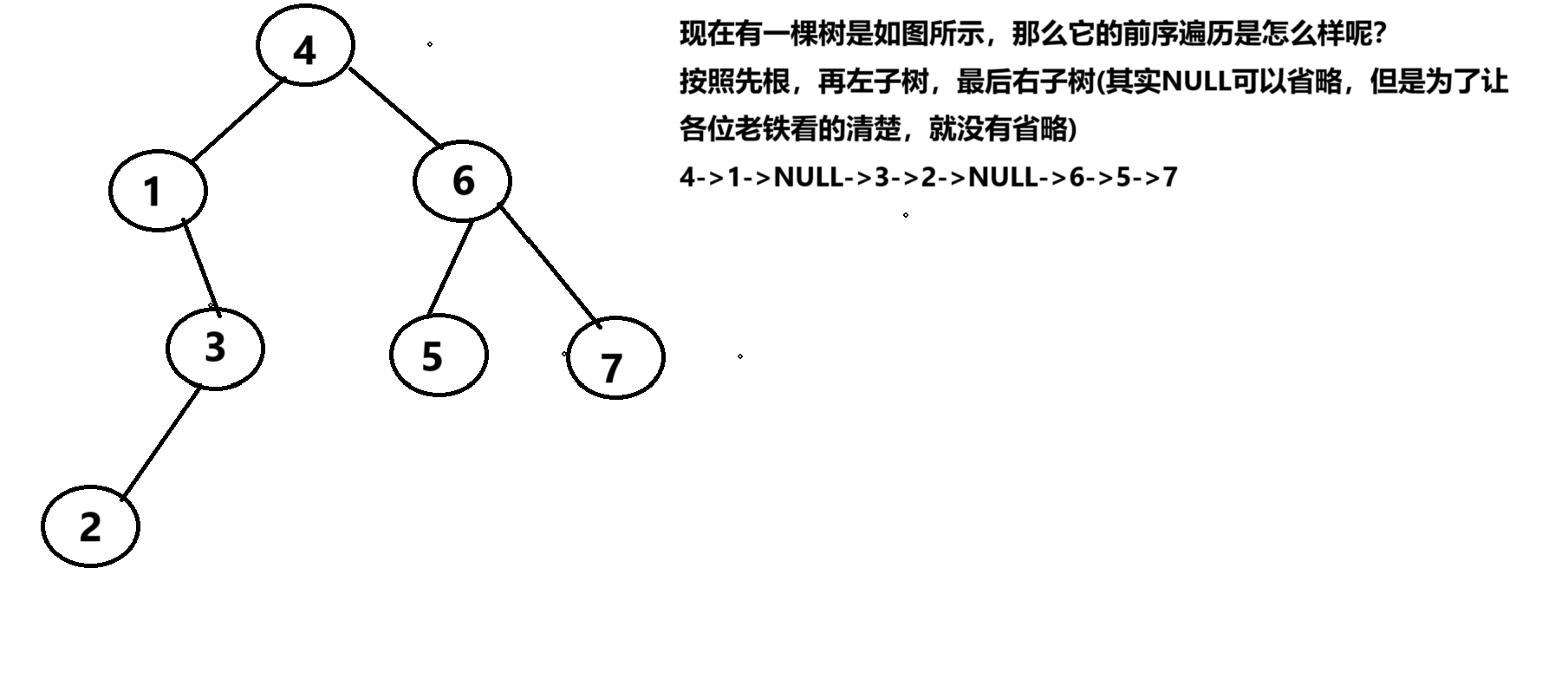
那么代码该如何写呢?代码很简单,通过递归来进行前序遍历
#include <iostream>
using namespace std;struct Node
{int _data;Node* _left;Node* _right;
};Node* createNode(int val)
{Node* newnode = new Node;newnode->_data = val;newnode->_left = nullptr;newnode->_right = nullptr;return newnode;
}void PreOrder(Node* root)
{if (root == nullptr){cout << "NULL" << " ";return;}cout << root->_data << " ";//只有当这个节点不是叶子节点时,才递归打印if (root->_left != nullptr || root->_right != nullptr){PreOrder(root->_left);PreOrder(root->_right);}
}int main()
{//用来测试的构建二叉树的方法Node* node1 = createNode(4);Node* node2 = createNode(1);Node* node3 = createNode(6);Node* node4 = createNode(3);Node* node5 = createNode(5);Node* node6 = createNode(7);Node* node7 = createNode(2);node1->_left = node2;node1->_right = node3;node2->_right = node4;node4->_left = node7;node3->_left = node5;node3->_right = node6;PreOrder(node1);return 0;
}
看一下代码结果吧

代码结果毫无问题,那么到这里我们已经懂得了二叉树的前序遍历,那么接下来就到二叉树的中序遍历了。
(2)二叉树的中序遍历:先左子树,再根,最后再右子树
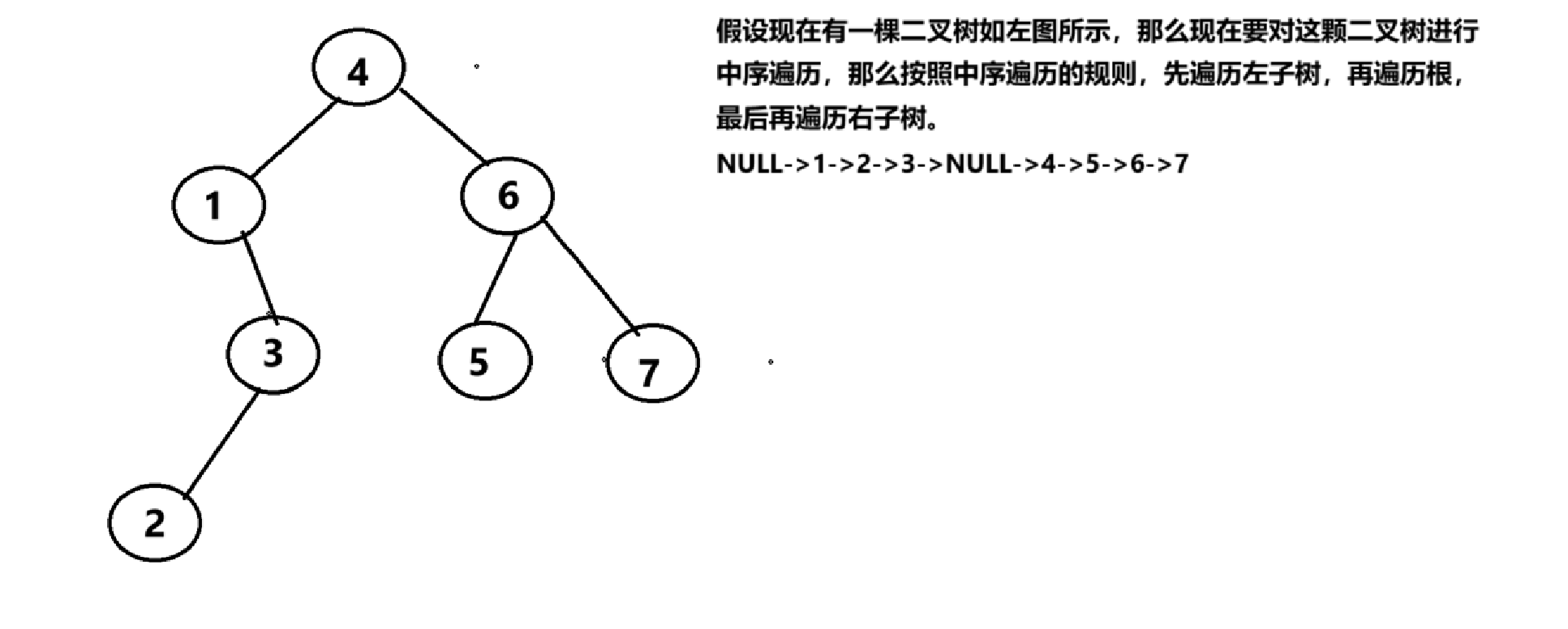
懂得了遍历规则,那么废话就少说了,直接上代码帮助各位老铁理解二叉树的中序遍历。
#include <iostream>
using namespace std;struct Node
{int _data;Node* _left;Node* _right;
};Node* createNode(int val)
{Node* newnode = new Node;newnode->_data = val;newnode->_left = nullptr;newnode->_right = nullptr;return newnode;
}void PreOrder(Node* root)
{if (root == nullptr){cout << "NULL" << " ";return;}//先保证这个节点不是叶子节点才能进行递归遍历if (root->_left != nullptr||root->_right!=nullptr){PreOrder(root->_left);}cout << root->_data << " ";//先保证这个节点不是叶子节点才能进行递归遍历if (root->_left != nullptr||root->_right != nullptr){PreOrder(root->_right);}
}int main()
{//用来测试的构建二叉树的方法Node* node1 = createNode(4);Node* node2 = createNode(1);Node* node3 = createNode(6);Node* node4 = createNode(3);Node* node5 = createNode(5);Node* node6 = createNode(7);Node* node7 = createNode(2);node1->_left = node2;node1->_right = node3;node2->_right = node4;node4->_left = node7;node3->_left = node5;node3->_right = node6;PreOrder(node1);return 0;
}
直接上代码结果,看看结果是否正确

(3)二叉树的后序遍历:规则是先左子树,再右子树,最后才是根
还是老样子,先画图说明规则
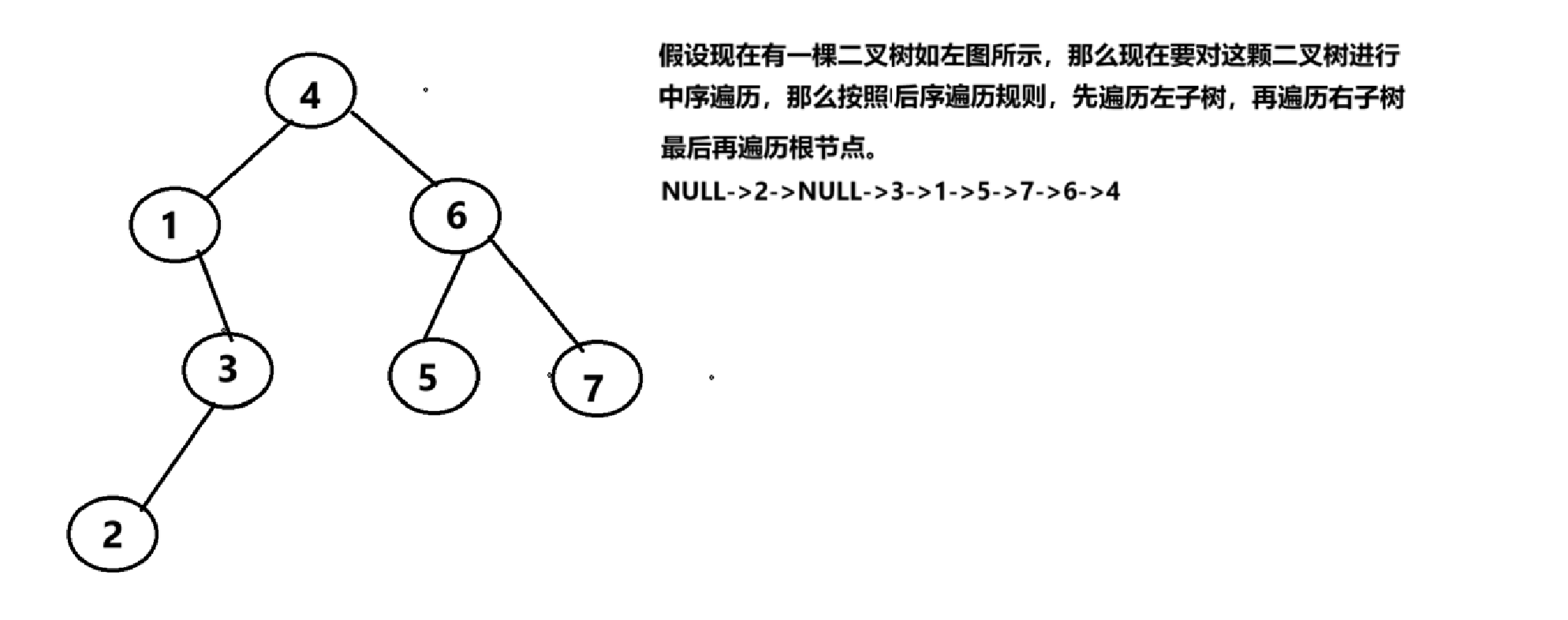
#include <iostream>
using namespace std;struct Node
{int _data;Node* _left;Node* _right;
};Node* createNode(int val)
{Node* newnode = new Node;newnode->_data = val;newnode->_left = nullptr;newnode->_right = nullptr;return newnode;
}void PreOrder(Node* root)
{if (root == nullptr){cout << "NULL" << " ";return;}//先保证这个节点不是叶子节点才能进行递归遍历if (root->_left != nullptr||root->_right!=nullptr){PreOrder(root->_left);}//先保证这个节点不是叶子节点才能进行递归遍历if (root->_left != nullptr || root->_right != nullptr){PreOrder(root->_right);}cout << root->_data << " ";
}int main()
{//用来测试的构建二叉树的方法Node* node1 = createNode(4);Node* node2 = createNode(1);Node* node3 = createNode(6);Node* node4 = createNode(3);Node* node5 = createNode(5);Node* node6 = createNode(7);Node* node7 = createNode(2);node1->_left = node2;node1->_right = node3;node2->_right = node4;node4->_left = node7;node3->_left = node5;node3->_right = node6;PreOrder(node1);return 0;
}
看看代码结果是否正确

(4)二叉树的层序遍历:二叉树层序遍历是层层遍历,我们需要借助队列先进先出的属性来进行遍历
下面笔者为各位老铁画图理解一下二叉树的层序遍历。

二叉树层序遍历的代码实现也很简单,笔者就直接上代码,然后看结果了。
#include <iostream>
#include <queue>
using namespace std;struct Node
{int _data;Node* _left;Node* _right;
};Node* createNode(int val)
{Node* newnode = new Node;newnode->_data = val;newnode->_left = nullptr;newnode->_right = nullptr;return newnode;
}void LevelOrder(Node* root)
{//如果二叉树是空树,那么直接返回if (root == nullptr) return;queue<Node*> q;q.push(root);while (!q.empty()){auto t = q.front();q.pop();cout << t->_data << " ";//当左右子树不为空时,进队列if (t->_left != nullptr) q.push(t->_left);if (t->_right != nullptr) q.push(t->_right);}
}
int main()
{//用来测试的构建二叉树的方法Node* node1 = createNode(4);Node* node2 = createNode(1);Node* node3 = createNode(6);Node* node4 = createNode(3);Node* node5 = createNode(5);Node* node6 = createNode(7);Node* node7 = createNode(2);node1->_left = node2;node1->_right = node3;node2->_right = node4;node4->_left = node7;node3->_left = node5;node3->_right = node6;LevelOrder(node1);return 0;
}
看看结果吧
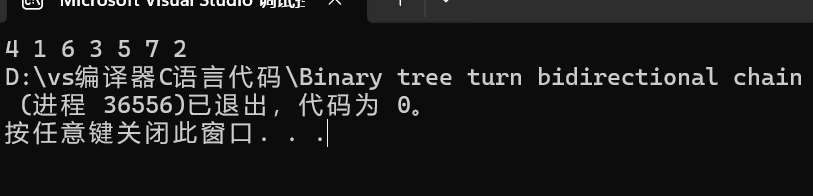
结果完全没问题,到这里二叉树的所有遍历方式就讲完了,接下来就是将二叉树如何实现了。
9.二叉树的实现
(1)构建二叉树(使用二叉链进行构建)(根据后序和中序来构建)
当我们想要构建一个二叉树时,我们需要先明白二叉树的一个节点中有什么,在二叉树中,每一个节点是不是都要有一个整形来存放该节点的值,还需有两个指针分别指向该节点的左孩子节点和右孩子节点
struct Node
{int _data;Node* _left;Node* _right;};
当我们构建二叉树时,是不是要在堆上开辟空间来创建节点,你的二叉树节点总不可能凭空产生吧,那么如何创建一个节点呢,下面笔者直接就上代码了,很简单的。
Node* createNode(int val)
{Node* node = new Node;node->_data = val;node->_left = nullptr;node->_right = nullptr;
}
到这里,二叉树的节点就创建好了,那么我们就需要基于二叉树的后序遍历和中序遍历来构建二叉树了。
ps:对于不懂得根据中序遍历和后序遍历还原出树的老铁,建议去b站搜一下视频讲解,笔者在这里就不使用文字讲解了,文字讲解笔者认为更难理解。
创建二叉树的思路

#include <iostream>
#include <vector>
#include <queue>
using namespace std;struct Node
{int _data;Node* _left;Node* _right;//构造Node() = default;Node(int val) :_data(val), _left(nullptr),_right(nullptr){}
};Node* createNode(int val)
{Node* newnode = new Node;newnode->_data = val;newnode->_left = nullptr;newnode->_right = nullptr;return newnode;
}Node* createTree(int* post_tree, int* infix_tree,int n)//n表示二叉树结点个数
{if (n == 0) return nullptr;else if (n == 1) return createNode(*(post_tree));//只有一个结点else{//先找到中序遍历的根节点Node* root = createNode(*(post_tree+n-1));int index = 0;for (int i = 0; i < n; i++){if (*(infix_tree+i) == root->_data){index = i;break;}}root->_left=createTree(post_tree, infix_tree, index);root->_right=createTree(post_tree + index, infix_tree + index + 1, n - index - 1);//-1是为了减去根节点return root;}
}int main()
{int post_tree[7] = {2,3,1,5,7,6,4};//后序遍历int infix_tree[7] = {1,2,3,4,5,6,7};//中序遍历createTree(post_tree, infix_tree, 7);return 0;
}
到这里,根据后序遍历和中序遍历来创建二叉树的代码就写好了,接下来笔者需要带各位老铁测试一下我们写的代码对不对,笔者使用二叉树的层序遍历来进行测试,看看使用刚刚创建的二叉树能不能正确的进行层序遍历。
#include <iostream>
#include <vector>
#include <queue>
using namespace std;struct Node
{int _data;Node* _left;Node* _right;//构造Node() = default;Node(int val) :_data(val), _left(nullptr),_right(nullptr){}
};Node* createNode(int val)
{Node* newnode = new Node;newnode->_data = val;newnode->_left = nullptr;newnode->_right = nullptr;return newnode;
}void LevelOrder(Node* root)
{//如果二叉树是空树,那么直接返回if (root == nullptr) return;queue<Node*> q;q.push(root);while (!q.empty()){auto t = q.front();q.pop();cout << t->_data << " ";//当左右子树不为空时,进队列if (t->_left != nullptr) q.push(t->_left);if (t->_right != nullptr) q.push(t->_right);}
}Node* createTree(int* post_tree, int* infix_tree,int n)//n表示二叉树结点个数
{if (n == 0) return nullptr;else if (n == 1) return createNode(*(post_tree));//只有一个结点else{//先找到中序遍历的根节点Node* root = createNode(*(post_tree+n-1));int index = 0;for (int i = 0; i < n; i++){if (*(infix_tree+i) == root->_data){index = i;break;}}root->_left=createTree(post_tree, infix_tree, index);root->_right=createTree(post_tree + index, infix_tree + index + 1, n - index - 1);//-1是为了减去根节点return root;}
}int main()
{int post_tree[7] = {2,3,1,5,7,6,4};//后序遍历int infix_tree[7] = {1,2,3,4,5,6,7};//中序遍历Node* root=createTree(post_tree, infix_tree, 7);LevelOrder(root);return 0;
}
看看代码结果吧
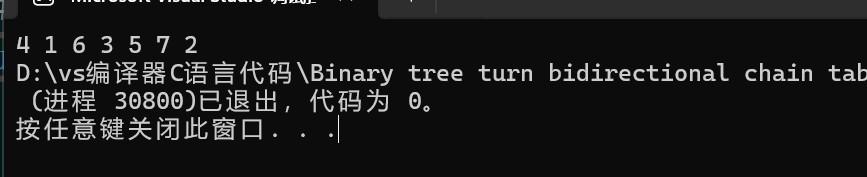
那么就可以证明我们创建的树是正确的。
其实还有一种根据前序遍历和中序遍历来创建二叉树的方式,如果各位老铁能理解笔者写的根据后序和中序来创建二叉树的代码,相信根据前序和中序来创建二叉树的代码对各位老铁来说就不是什么问题了。
