算法【1】

网址：主站

工具补充

1. sort 函数的使用规则

• 作用：对容器元素进行排序，默认升序。
• 语法：sort(起始迭代器, 结束迭代器, 比较规则)
  • 前两个参数是排序范围：[begin, end)（包含begin，不包含end）。
  • 第三个参数可选：自定义比较规则（默认用 < 比较，即升序）。
• 代码场景：
  sort(jobs.begin(), jobs.end(), [](const vector<int>& a, const vector<int>& b) { return a[1] < b[1]; })
  表示按 jobs 中每个子数组的第二个元素（结束时间）升序排序。
  • 为什么用 <？因为比较规则返回 true 时，a 会排在 b 前面。a[1] < b[1] 意味着“结束时间小的 job 排在前面”，即升序。

2. begin() 和 end() 迭代器

• 迭代器：可理解为“容器元素的指针”，用于访问容器元素。
• begin()：返回指向容器第一个元素的迭代器。
• end()：返回指向容器最后一个元素之后的迭代器（标记范围终点，不指向实际元素）。
• 用途：搭配算法（如 sort）指定操作范围，形成 [begin, end) 左闭右开区间，确保遍历/排序不越界。

3. Lambda 表达式（匿名函数）

• 格式：[捕获列表](参数列表) { 函数体 }
  此处 [] 表示无捕获，(const vector<int>& a, const vector<int>& b) 是参数，{ return a[1] < b[1]; } 是函数体。
• 作用：临时定义短小的函数，作为 sort 等算法的自定义比较规则。
• 代码场景：告诉 sort 如何比较两个 job——用它们的结束时间（a[1] 和 b[1]）比较，实现按结束时间排序。

4. rbegin() 反向迭代器

• 作用：返回容器的反向起始迭代器，指向容器最后一个元素（与 begin() 方向相反）。
• 代码场景：dp.rbegin() 指向 map 中键最大的元素（因为 map 按键升序排列，最后一个元素键最大）。
  dp.rbegin()->second 即获取当前最大时间对应的最大利润（不选择当前工作时的最大利润）。

5. ->second 访问 map 的值

• map 存储的是键值对（pair<key, value>），迭代器指向 pair 对象。
• ->first：访问键（key）；->second：访问值（value）。
• 代码场景：dp 中键是时间，值是该时间的最大利润。prev(...)->second 即获取“开始时间前的最大利润”。

6. prev() 函数

• 作用：返回迭代器的前一个位置（即 --iterator 的结果），需迭代器支持 -- 操作（如 map 的迭代器）。
• 代码场景：prev(dp.upper_bound(begin)) 用于获取“最后一个键 <= begin 的元素迭代器”（配合 upper_bound 查找）。

7. 二分相关库函数汇总

核心逻辑关联

代码通过 sort 按结束时间排序 jobs，用 map 存储“时间-最大利润”映射，借助 upper_bound+prev 快速找到不冲突的历史最大利润，用 rbegin 获取当前最大利润，最终通过动态规划选择最优解。这些工具共同实现了高效的时间复杂度（O(nlogn)）。

排序算法

排序关键指标：

1. 时空复杂度；
2. 排序稳定性：
   • 排序后相对位置没有发生改变，单单排int类型意义不大，但是对于复杂的数据，比如订单数据，有订购时间和用户id，那如果是稳定排序，排序后相同用户id依然会按照交易日期有序排列；
   • 如果用不稳定排序，相同用户id的订单相对位置可能变化，
3. 是否原地排序：是否不需要额外的辅助空间，只需要常数级别额外空间？能否最直接操作原数组？

1. 选择排序【不稳定】

• 遍历一遍数组，找到最小值
• 与数组第一个元素交换
• 接着从第二个开始重复以上操作

void sort(vector<int>& nums) {int n = nums.size();// sortedIndex 是一个分割线// 索引 < sortedIndex 的元素都是已排序的// 索引 >= sortedIndex 的元素都是未排序的// 初始化为 0，表示整个数组都是未排序的int sortedIndex = 0;while (sortedIndex < n) {// 找到未排序部分 [sortedIndex, n) 中的最小值int minIndex = sortedIndex;for (int i = sortedIndex + 1; i < n; i++) {if (nums[i] < nums[minIndex]) {minIndex = i;}}// 交换最小值和 sortedIndex 处的元素int tmp = nums[sortedIndex];nums[sortedIndex] = nums[minIndex];nums[minIndex] = tmp;// sortedIndex 后移一位sortedIndex++;}
}

• 空间复杂度是 O(1)，是个原地排序。
• 时间复杂度 $O(n^2)$，嵌套for循环
• 数组本来有序性对算法执行次数的影响：无影响，即便原本有序，也会执行$O(n^2)$
• 非稳定排序：交换操作使排序失去了稳定性，无法维持原来相等元素的相对位置。

2. 冒泡排序【拥有稳定性】

选择排序三大问题：

• 不稳定，交换导致改变相同元素相对位置
• 时间复杂度与初始有序度无关，即便一开始是完全有序，时间复杂度还是$O(n^2)$
• 执行次数大概是$(n^2)/2$，无法优化

1. 优化稳定性

选择排序将最小值交换到最前面，

• 最小值放到前面这一步本身不会破坏稳定性，

• 将最前面的值放到最小值的位置，自然就破坏了最前面值原本的稳定性。

• 所以，我们还是将最小值放到最前面，但是最前面的值不再直接放到最小值位置，而是整体向后移动。

// 对选择排序进行第一波优化，获得了稳定性
void sort(vector<int>& nums) {int n = nums.size();int sortedIndex = 0;while (sortedIndex < n) {// 在未排序部分中找到最小值 nums[minIndex]int minIndex = sortedIndex;for (int i = sortedIndex + 1; i < n; i++) {if (nums[i] < nums[minIndex]) {minIndex = i;}}// 优化：将 nums[minIndex] 插入到 nums[sortedIndex] 的位置// 将 nums[sortedIndex..minIndex] 的元素整体向后移动一位int minVal = nums[minIndex];// 数组搬移数据的操作for (int i = minIndex; i > sortedIndex; i--) {nums[i] = nums[i - 1];}nums[sortedIndex] = minVal;sortedIndex++;}
}

获得了稳定性，但是执行效率降低了，因为变成了双层for循环外加一次for循环，执行次数远大于$n^2/2$。

第一次双层for循环找到最小值
第二次for循环将最小值插入，并且整体后移

2. 优化时间复杂度
继续优化时间复杂度，合并上面两次for循环，实现了冒泡排序的本质：倒序遍历n次，每次都边找最小值边排序，即交换逆序对

• n次倒序遍历nums[sortedIndex…]
• 如果发现了逆序对就交换顺序
• 这样nums[sortedIndex…]的最小值就是慢慢移动到nums[sortedIndex]
• 全程只交换相邻逆序对，完全不动相同元素，所以稳定排序。
• 冒泡排序，从尾部向头部冒泡

void sortVector<vector<int>& nums> {int n = nums.size();// sortedIndex前面都是有序的int sortedIndex = 0;	// n次遍历！每次把当前最小的值pop到最前面也就是sortedIndex = 0位置while (sortedIndex = 0) {  for (int i = n - 1; i > sortedIndex; i-- ) {// 如果发现一次逆序对(前>后)就交换if (nums[i - 1] > nums[i]) {// swap交换逆序对int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;}}// 成功把最小值pop到前面一次sortedIndex++; 										}
}

这个算法的名字叫做冒泡排序，因为它的执行过程就像从数组尾部向头部冒出水泡，每次都会将最小值顶到正确的位置。

3. 提前终止
还有个优化点，那就是选择排序和目前的冒泡排序都是与数组原始有序性无关的，即便已经有序，也会执行$O(n^2)$次，我们可以想办法检测有序性提前终止程序。
flag编程：用这个标记编程的思想，如果某次倒序遍历完全没有找到逆序对，没有发生swap，则说明已经有序，不需要继续执行程序！
只需要加一个bool值，记录每次倒序遍历是否发生swap即可！

void sortVector<vector<int>& nums> {int n = nums.size();int sortedIndex = 0;	while (sortedIndex = 0) {  // 设置flag, 初始化没有发生swapbool swapped = false; for (int i = n - 1; i > sortedIndex; i-- ) {if (nums[i - 1] > nums[i]) {int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;// 如果发生了swap，设为truebool swapped = true;}}// 如果某次遍历完全没有swap,说明已经有序，退出程序if (!swapped) break; sortedIndex++; 										}
}

3. 插入排序【逆向思维】【扑克牌抓牌】

对选择排序不稳定的问题，我们有一些解决办法了：

• 保住稳定性：我们提出了一次for循环找到最小值，最小值放在最前面，然后再一次for循环把其他元素都逐一往后排，保住了排序的稳定性；
• 冒泡排序：倒序遍历 + 交换逆序对 + flag编程提前终止
• 成功合并了for循环，还有其他方法把while里面的两个for优化成一个for循环么？

逆向思维：

• 前面两种算法都是在后面 nums[sortedIndex…] 中找到最小值，然后将其插入到 前面nums[sortedIndex] 的位置，这两步操作就是两次for循环。
• 反过来想，能不能在nums[0…sortedIndex-1] 这个部分有序的数组中，找到 nums[sortedIndex] 应该插入的位置，然后进行插入呢？
  • 有序数组 nums[0…sortedIndex-1] 找到应该插入的位置，很自然想到用二分查找，这样就可以把第一次for循环$O(n)$优化为$O(log(n))$
  • 但是找到后还得交换，又是一次for循环
  • 还不如继续用冒泡的思想，一边找一边换？

// 对选择排序进一步优化，向左侧有序数组中插入元素
// 这个算法有另一个名字，叫做插入排序
void sort(vector<int>& nums) {int n = nums.size();// 维护 [0, sortedIndex) 是有序数组int sortedIndex = 0;while (sortedIndex < n) { // 将 nums[sortedIndex] 插入到有序数组 [0, sortedIndex) 中// 依旧是倒序遍历，交换逆序对！for (int i = sortedIndex; i > 0; i++) {if (nums[i] < nums[i-1]) {int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;} else { // 到了该到的位置了！换不下去了！break;}}sortedIndex++;}

插入排序就像是打扑克，把新抓到的牌放到已经排好序的牌中：

1. 原地排序算法：空间复杂度
2. 时间复杂度依旧是$O(n^2)$，实际操作次数大约是$n^2/2$次
3. 稳定排序：只有在 nums[i] < nums[i - 1] 的情况下才会交换元素，所以相同元素的相对位置不会发生改变。
4. 与初始有序度强相关：
   • 初始有序度高，仅有个别元素逆序，则内层负责swap的for循环几乎不操作，时间复杂度接近$O(n)$；
   • 初始完全逆序，插入排序效率极低，每次都与nums[0…sortedIndex-1] 所有元素交换，总时间复杂度极为接近$O(n^2)$。
   • 插入排序的实际操作次数会小于冒泡排序的

4.

理解h有序数组：

• 间隔h位置，是有序的数组

希尔排序是基于选择排序进行优化的

• 插入排序的问题：上来就想一步到位，直接把乱序数组变成1有序数组
• 希尔的概念是不着急，先变成16有序数组，然后8有序数组，4，2，最后变成1有序数组，完成排序！

插入排序三步改动实现希尔排序：见代码

// 希尔排序本质：对h有序数组进行插入排序
// 逐步缩小h
void sort(vector<int>& nums) {int n = nums.size();// 设置生成函数 2^(k-1)// 即 h = 1，2，3，4，...int h = 1;while (h < n/2) {	// h放到最大h = 2 * h;}// 改动一：插入排序所有逻辑套在h的while循环中while (h >= 1) {// 改动二：sortedIndex 初始值设置为 h ，而不是1int sortedIndex = h;while (sortedIndex < n) {// 改动三：把比较和交换元素的步长设置为h，而不是相邻元素 // 依旧是倒序遍历，交换逆序对（相隔h）！// 原来是： for (int i = sortedIndex; i > 0; i--) {for (int i = sortedIndex; i >= h; i-=h) {if (nums[i] < nums[i-h]) { // 减1都换成减hint tmp = nums[i];nums[i] = nums[i-h];nums[i-h] = tmp;} else { // 到了该到的位置了！换不下去了！break;}}sortedIndex++;}// 按照递增函数的规则，缩小hh /= 2;}
}

• 时间复杂度终于低于$O(n^2)$
• 原地排序：空间复杂度 $O(1)$
• 不稳定排序，打乱了相同元素的顺序！

5. 快速排序【妙用二叉树前序位置】

6.

7.

8.

9.

10.

数据结构

链表题

数组题

双指针

滑窗

二分搜索

前缀和

差分

队列/栈

实现队列/栈

经典

单调栈

单调队列

二叉树&递归

二叉树核心框架

递归 + 遍历

递归 + 分解

层序遍历

数据结构设计

LRU

LFU

经典设计

图论

图结构通用代码

图的逻辑结构

图的逻辑结构构成：

• 节点vertex
• 边edge

图节点的逻辑结构：

// 图节点实现
class Vertex {
public:int id;std::vector<Vertex*> neighbors;
};

图其实就是多叉树：

// 多叉树节点结构
class TreeNode {
public:int val;std::vector<TreeNode*> children;
};

以上只是逻辑上的构成，实际应用中，很少用这个 Vertex类。

邻接表和邻接矩阵实现图结构

比如一幅图：

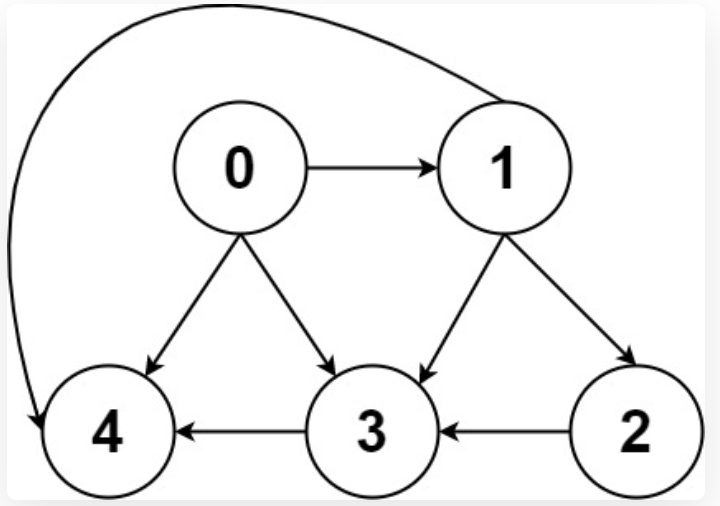
有两种表示方法：

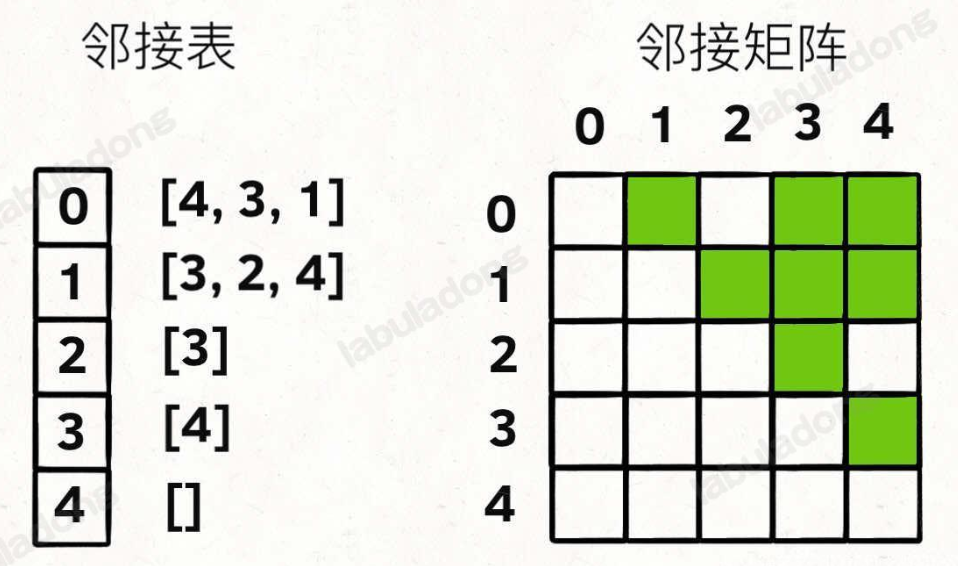
邻接表很直观，我把每个节点 x 的邻居都存到一个列表里，然后把 x 和这个列表映射起来，这样就可以通过一个节点 x 找到它的所有相邻节点。

邻接矩阵则是一个二维布尔数组，我们权且称为 matrix，如果节点 x 和 y 是相连的，那么就把 matrix[x][y] 设为 true（上图中绿色的方格代表 true）。如果想找节点 x 的邻居，去扫一圈 matrix[x][…] 就行了

// 邻接表：graph[x] 存储 x 指向的 所有邻居节点
vector<vector<int>> graph;// 邻接矩阵：matrix[x][y] 记录 x 是否有 一条指向 y 的边
vector<vector<bool>> matrix;

分别适用于不同场景
分析两种存储方式的空间复杂度，对于一幅有 V 个节点，E 条边的图，邻接表的空间复杂度是
O
(
V
+
E
)
O(V+E)，而邻接矩阵的空间复杂度是
O
(
V
2
)
O(V
2
)。

所以如果一幅图的 E 远小于 V^2（稀疏图），那么邻接表会比邻接矩阵节省空间，反之，如果 E 接近 V^2（稠密图），二者就差不多了。

在后面的图算法和习题中，大多都是稀疏图，所以你会看到邻接表的使用更多一些。

邻接矩阵的最大优势在于，矩阵是一个强有力的数学工具，图的一些隐晦性质可以借助精妙的矩阵运算展现出来。不过本文不准备引入数学内容，所以有兴趣的读者可以自行搜索学习。

这也是为什么一定要把图节点类型转换成整数 id 的原因，不然的话你怎么用矩阵运算呢？

环检测

拓扑排序

二分图判定

并查集

最小生成树

Dijkstra 最短路径算法

DFS / 回溯

BFS

动态规划

动归核心框架

子序列问题

背包问题

0-1背包问题

物品有两个属性：重量wt 和 价值 val
背包有两个属性：载重W 和 容量N（最多装几个物品）
问：最多能装多少价值的东西？

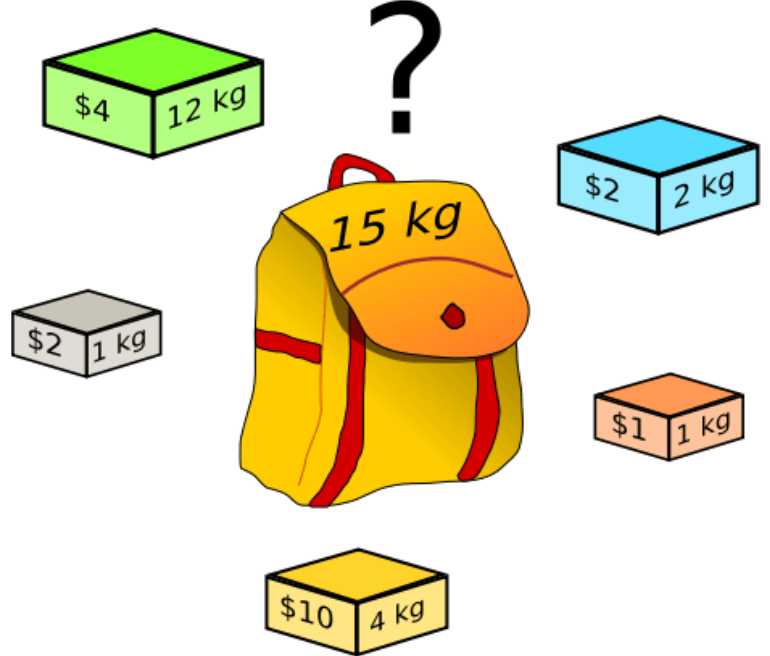
解法：动态规划
第一步：确定「状态」和「选择」
从背包的状态和物品的状态出发：

• 状态：即描述当前问题的局面（即背包的状态和物品的状态，不涉及选择），从「可选择的前i个物品 」「可用的容量 」；

• 选择：对于每件商品，选择「装进背包」或者「不装进背包」；

  自顶而下的代码框架：

  for 状态1 in 状态1的所有取值：for 状态2 in 状态2的所有取值：for ...dp[状态1][状态2][...] = 择优(选择1，选择2...)
  

第二步：定义dp数组， 某个状态的最优解

• 从状态出发：涉及两个东西的状态，所以需要二维数组dp[ ][ ]；

• dp[ i ][ w ] 定义为：前 i 个物品情况下（ 选择了某些物品，背包容量剩余 w ）此时，选择i 以及 w的情况，价值最大为dp[i][w]；

• 例如： dp[3][5] = 6，表示：对于给定的一堆物品，一个背包，若限制从前三个物品选，当选了某些东西，容量为5时最优，价值为6；

• base case：dp[0][…] = dp[][0] = 0，物品数为0或者背包空间为0时，就是base case，为0；

  // 注意，最多N个物品，最大W的容量
  int[][] dp[N][W];
  dp[0][...] = 0;
  dp[...][0] = 0;
  for i in [1...N]:for w in [1...W]:dp[i][w] = max {把物品 i 放进背包不放 i}
  return dp[N][W];
  

第三步：根据「选择」，思考状态转移的逻辑

从dp定义出发：dp[i][w] 表示：对于前 i 个物品（从 1 开始计数），当前背包的容量为 w 时，这种情况下可以装下的最大价值是 dp[i][w]。
关键的选择是：

• 如果没有把第i个物品放入背包（w没有变）：dp[i][w]直接继承dp[i-1][w]，dp[i][w] = dp[i-1][w]
• 如果把第i个物品放入背包：dp[i][w] = val[i] + dp[i-1][W-wt[i-1]];(要在剩余容量的限制下，在前i-1个里面挑选，求最大值，也就是dp[i-1][W-wt[i-1]])

for i in [1..N]:for w in [1..W]:dp[i][w] = max(dp[i-1][w],dp[i-1][w - wt[i-1]] + val[i-1])
return dp[N][W]

最后一步：边界条件处理

#include <cassert>
// W 背包限重，wt[]，val[]
int knapsack(int W, vector<int>& wt, vector<int>& val) {int N = val.size();// 定义dp 并直接初始化0// dp[i][w] 限制前i个可选 + 限重w 时的最大价值vector<int> dp(N + 1, vector<int>(W + 1));for (int i = 1; i <= N; i++) { 			// 状态1：for (int w = 1; w <= W; w++) {		// 状态2：// 注意处理，可能有的物品wt[i]重量大于当前限重w// 则直接跳过dp[i][w]?那只能说明不能选i// 强制不选i，即dp[i][w] = dp[i-1][w]if (wt[i] > w) {dp[i][w] = dp[i-1][w];}else { dp[i][w] = max(val[i] + dp[i-1][w-wt[i]] // 选择1dp[i-1][w]				 // 选择2);}}}return dp[N][W];
}

474. 一和零

vector<int> dp(N+1, vector<int>(W + 1));
dp[i][w]	// 只能【选前i个物品】，【限重w】情况下，最大价值为dp[i][w]

dp[i][j][k]	// 只能【选前i个物品】，【0 最大限制j个】【1 最大限制k个】情况下，最大数量为dp[i][j][k]

class Solution {
public:int findMax(vector<string>& strs, int m, int n) {// 定义dp：dp[][][]// 如果只能选前i个元素，最多选j个0，最多选k个1；// 可以装的最大字符串数为 dp[i][j][k]// 注意三维数组的定义方式l = strs.size();vector<vector<vector<int>>> dp(l + 1, vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));// base case：dp[0][...][...] = 0 没有任何字符串可选时，最大可装的数量是0// 从 base case 开始状态转移 ， 从 1 到 nfor (int i = 1; i <= l; i++) {// 注意存在一个索引偏移，dp[i][][] 的i是第i个的意思，对应到strs 的当前char索引是i-1string curStr = strs[i - 1];// 统计当前curStr(物品)的0数量和1数量(重量)int zeroCount = 0;int oneCount = 0;for (char c : curStr) {if (c == '0') zeroCount++;else oneCount++;}// 根据要不要选 curStr 进行状态转移for (int j = 0; j <= m;j++) {for (int k = 0; k <= n;k++) {// 检查当前物品curStr的重量zeroCount oneCount是否小于背包容量限制为j和kif (j >= zeroCount && k >= oneCount) {dp[i][j][k] = max(dp[i - 1][j][k],1 + dp[i - 1][j - zeroCount][k - oneCount]										);} else {					// 背包容量不足时，强制选择不放curStr！dp[i][j][k] = dp[i - 1][j][k];	// }}} }// return dp[l][m][n];}
};

1262. 可以被3整除的最大和

// 定义dp
dp = vector<int>(nums.size());

class Solution {
public:int maxSumDivThree(vector<int>& nums) {// 定义：nums[0..i] 中，和 3 相除余数为 j 的最大和是 dp[i][j]// 3 is dp[i][j]int n = nums.size();// dp[0][0/1/2]要作为base case，所以总共有n+1个情况vector<vector<int>> dp(n + 1, vector<int>(3, INT_MIN));// base casedp[0][0] = 0;dp[0][1] = INT_MIN;dp[0][1] = INT_MIN;// 状态转移方程：根据第i个数字nums[i]以及前i-1个数字的余数情况dp[i-1][1/2/3]// 来推导前i个数字的余数情况 dp[i][0/1/2] for (int i = 1; i <= nums; i++) {int curNum = nums[i - 1]; if (curNum % 3 == 0) {	// 当前元素curNum余数0，则前面元素和余数是多少，加上curNum之后还是多少，就看要不要加curNum【选择】dp[i][0] = max(curNum + dp[i - 1][0], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][1], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][2], dp[i - 1][2]);} else if (curNum % 3 = 1) { 	// 选不选余数为1的curNum？dp[i][0] = max(curNum + dp[i - 1][2], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][0], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][1], dp[i - 1][2]);} else { // curNum余数是2dp[i][0] = max(curNum + dp[i - 1][1], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][2], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][0], dp[i - 1][2]);		}}// 最后返回前i个元素的能被3整除最大和，即余数为0，dp[n][0]return dp[n][0];}
};

1235. 规划兼职工作

这次物品变成了不同的工作，每份工作有开始时间、结束时间、以及对应的价值，收益。
当然不可能分身，所以同一个时刻只能做一份工作，返回最大收益。
这也是0-1的变种问题：
0-1的状态是【前i个物品】【限重w】情况下，【选择】选不选当前的物品，使得当前价值最大；
这里的物品就是工作，工作有【开始时间】【结束时间】【收益】三个属性，打包到一起，【选择】选不选当前的工作，使得收益最大。
状态是：【前i个工作可选】？直接用endTime作为可选时间吧！

class Solution {
public:int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {// 物品的三个属性打包到一起，方便排序int n = profit.size();vector<vector<int>> jobs(n, vector<int>(3));for (int i = 0; i < n;i++) {jobs[i] = {startTime[i], endTime[i], profit[i]};}// 用sort(起始，结束（开区间）， 排序规则 )；按end时间排序sort(jobs.begin(), jobs.end(), [](const vector<int> a, vector<int> b) {return a[1] < b[1];});// 至此已经按照一定顺序排列好了 “物品”map<int, int> dp;for (const auto& job : jobs) {// 提取出job的三个属性  int begin = job[0];int end = job[1];int value = job[2];// 进行选择，穷举所有选择dp[end] = max(// 选当前job，收益增加value，但是[begin, end)这段时间被占用了！// [begin, end)时间段内的工作都不行，[0,begin)内的任务可以// 用二分手段查找第一个结束时间大于等于begin的dp结果：dp.upper_bound(begin)// 这个的前一个prev就是不在[begin, end)区间内的选择的最大收益// 最后一个键 <= begin 的元素迭代器// dp<int, int> 第一个元素键是截至end ： 第二个元素值是收益value + prev(dp.upper_bound(begin))->second,// 不选当前job，则当前job[end]的值直接继承上一个end的值(保存现有最大值)dp.rbegin()->second; // rbegin()指向容器最后一个元素);}return dp.rbegin()->second;}
};

子集背包问题——LC.416 分割等和子集

输入一个只包含正整数的非空数组 nums，请你写一个算法，判断这个数组是否可以被分割成两个子集，使得两个子集的元素和相等。
比如说输入 nums = [1,5,11,5]，算法返回 true，因为 nums 可以分割成 [1,5,5] 和 [11] 这两个子集。
如果说输入 nums = [1,3,2,5]，算法返回 false，因为 nums 无论如何都不能分割成两个和相等的子集。

这个问题看起来和背包没啥关系啊？
0-1背包问题：求出【可装载重量W】【N个物品（每个物品价值v，重量w）】情况下，求出背包可装载最大价值。
分割子集要求：判断能否分割成两个和相等的子集，实际上，如果有一个子集可以凑成sum/2，另一半必然就是sum/2呀！
所以问题转化成了，背包【可装载重量 = sum/2】【N个物品（每个物品有重量nums[I]）】，问能不能恰好装满背包。

解法：
第一步：明确【状态】和【选择】

• 状态：跟0-1背包一样的，【可选择的物品】【背包当前容量】
• 选择：当前物品【装】【不装】

第二步：dp数组定义？base case？

• dp[i][j] = x：对于前i个物品可选（i从1开始计数？）， 背包容量j时，x为true表示可以装满，false表示不能恰好装满
• base case：没有物品可选时，dp[0][…] = 0；容量为0时，天然装满dp[…][0] = true；
• 最终返回的：N个物品时，能不能刚好凑到sum/2，return dp[N][sum/2]
• 举例：dp[4][9] 若只在前4个物品选择，有一种方案能够恰好把容量9的背包装满；或对于这道题，若只在前4个数字选择，存在一个子集的和为9；

第三步：根据【选择】分析状态转移的逻辑
也就是装不装第i个物品的问题（）：

• 不装：直接继承dp[i-1][j]
• 装：取决于dp[i-1][j - nums[i]]，如果装了第 i 个物品，就要看背包的剩余重量 j - nums[i-1] 限制下是否能够被恰好装满。如果 j - nums[i-1] 的重量可以被恰好装满，那么只要把第 i 个物品装进去，也可恰好装满 j 的重量；否则的话，重量 j 肯定是装不满的。

注意点：

• 上述分析都是第i个物品，所以与真实的nums索引差1
• 和为奇数的时候，必不可分
• 第i个物品（索引为i-1）的重量（nums[i - 1]） 大于背包总容量j时候，强制选择不装，装不了！

class Solution {
public:	bool canPartition(vector<int>& nums) {// 求sumint sum = 0;for (int num : nums) sum += num;// sum 为奇数，直接falseif (sum % 2 != 0) return false;// sum 偶数，继续int W = sum / 2;	// 定义dp[i][j]： i范围是0~n，j范围是0~Wint n = nums.size();vector<vector<int>> dp(n + 1, vector<int>(w + 1, false));// base case：初始化dp[0...n][0] = turefor (int i = 0; i >= n; i++) {dp[i][0] = true;			}// 状态转移：前提背包容量够， 且注意索引for (int i = 1; i <= n;i++) {	// 第i个选不选，索引是nums[i-1]选不选for (int j = 1; j <= W; j++) {	//// 如果 容量j 是足够的if (j >= nums[i - 1]) {// 装还是不装？dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];} else {	// 容量不够,肯定是装不了第i个物品 nums[i - 1]dp[i][j] = dp[i - 1][j];}}}// 返回return dp[n][W];}
};

优化空间复杂度，因为这道题的dp[i][j] 全靠上一行 dp[i - 1][…]转化过来！
之前的元素都不会在用，不用保存所有的行！

class Solution {
public:	bool canPartition(vector<int>& nums) {// 求sumint sum = 0;for (int num : nums) sum += num;// sum 为奇数，直接falseif (sum % 2 != 0) return false;// sum 偶数，继续int W = sum / 2;	// 定义dp[i][j]： i范围是0~n，j范围是0~Wint n = nums.size();// vector<vector<int>> dp(n + 1, vector<int>(w + 1, false));vector<int> dp(W + 1, false);// base case：初始化dp[0...n][0] = ture 即dp[0] = true// for (int i = 0; i >= n; i++) dp[i][0] = true;dp[0] = true;// 状态转移：前提背包容量够， 且注意索引for (int i = 0; i < n; i++) {	// 第i个选不选，索引是nums[i-1]选不选for (int j = 1; j <= W; j++) {	//// 如果 容量j 是足够的if (j >= nums[i]) {// 装还是不装？dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];}}}}// 返回// return dp[n][W];return dp[W];}
};

这段代码和之前的解法思路完全相同，只在一行 dp 数组上操作，i 每进行一轮迭代，dp[j] 其实就相当于 dp[i-1][j]，所以只需要一维数组就够用了。
唯一需要注意的是 j 应该从后往前反向遍历，因为每个物品（或者说数字）只能用一次，以免之前的结果影响其他的结果。
至此，子集切割的问题就完全解决了，时间复杂度O(n*sum)，空间复杂度
这句话没读懂啊，为啥会影响之前的其他结果？
为啥原来二维数组不用反向遍历？二维数组不能反过来遍历吧，前一个值都没有算出来，反过来不就不能利用上一个计算出来的值了吗？

chase4ever
Tokics
2023-04-19
这个要慢慢品，我理解了好久才悟到。

为什么不能正向遍历？因为外层遍历的是物品，0-1背包问题，一个物品只能选择一次，就是说，如果j正向遍历，容量从小到大可能多次选择这个品。
2.反向遍历，前面的数据都没计算，为什么j反向遍历正确？ 因为在计算dp[i][j]的时候，使用的是dp[i-1][j-v]的数据，即：只考虑0~i-1这么多物品的情况下的结果。这些都是完全计算过了的，反向遍历没有问题，且，反向遍历可以保证在j之前的容量里，一定没有考虑过这个物品。也就是说，当前可以决策是否装入i这个物品，是因为在这之前的容量没有考虑过是否装入i，保证i只能最多装入1次

子集背包问题——最后一块石头的重量II

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

这道题完全就是分割子集的变形题，每次碰碎出两块石头，得到y-x！要求出最后剩余的石头的最小值，分割子集问题中要找出是否存在两个相等子集，
举上一题的例子：
比如说输入 nums = [1,5,11,5]，算法返回 true，因为 nums 可以分割成 [1,5,5] 和 [11] 这两个子集。
如果说输入 nums = [1,3,2,5]，算法返回 false，因为 nums 无论如何都不能分割成两个和相等的子集。
这里 nums = [1,5,11,5]，这里 11 碰 1 得到 10 ，10 碰 5 得到 5， 5 碰 5，最后是0；
nums = [1,3,2,5]，这里 5 碰了 1 得到 4，4 碰了 2 得到 2， 2 碰 3 得到 1；

其实就是分割子集，使得子集的差最小，也就是使得两个子集的重量和都尽量接近sum/2！

所以问题转换成了背包问题：
给定容量sum/2的背包，若干石头stones，问背包能装下的最大重量maxWeight是？则一堆重量和是maxWeight，另外一堆重量和（sum - maxWeight）是最后返回（sum - maxWeight） - maxWeight；这就是消除不掉的石头的重量和！

所以

• dp[i][j] 定义：仅可以选择前i个石头，容量是j情况下，装的最大重量dp[i][j]
• base case ：
  • dp[0][…] = 0
  • dp[…][0] = 0
• 状态转移：选不选第i个（索引变换）石头？
  • 石头巨大，超容量j：强制不选，继承上个值
  • 可选可不选 第i个石头，stone[i - 1]：
    • 选stone[i - 1]： stone[i - 1] + dp[i ][j - stone[i - 1]]
    • 不选：继承

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {// 计算 sumint sum = 0;for (int stone : stones) sum += num;// 定义dp[i][j]：前i个石头可选，背包容量j 情况下，最多多重？  // i范围0~n 长度n+1， j范围0~W 长度W+1int n = stones.size(), W = sum / 2; vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));// base case：已经初始化！for (int i = 1; i <= n; i++) {int curStone = stones[i - 1];	// 索引问题for (int j = 1; j <= W; j++) {if (j < curStone) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = max(dp[i - 1][j],curStone + dp[i - 1][j - curStone]);}}}int maxWeight = dp[n][W];return sum - maxWeight * 2;}
};

完全背包问题——零钱兑换II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

很容易看出也是个背包类型的问题，跟前面最大的区别就是物品数量无限，称为完全背包问题。

第一步：确定状态和选择
状态：

• 背包的容量
• 可选择的物品
  选择：
• 装进背包
• 不装进背包
  动归框架：

for 状态1 in 状态1的所有取值：for 状态2 in 状态2的所有取值：for ...dp[状态1][状态2][...] = 计算(选择1，选择2...)

第二步：定义dp，要能从子问题推出新问题的dp！
从题意：求解凑出某个金额amout的方案数量，并且有两个状态可选择的物品和凑的金额
定义dp[i][j] : 若只能选前i种（注意！这里换成了“种”）物品（不限制数量，可重复），当容量j时，有dp[i][j]种方法可以填满背包容量j
换成这道题背景：
若只使用 coins 中的前 i 个（i 从 1 开始计数）硬币的面值，若想凑出金额 j，有 dp[i][j] 种凑法
base case ：

• dp[0][…] = 0；这一步很好想，没有选择，则方案必然为0
• dp[…][0] = ？；目标金额是0呢？什么都不做就已经完成目标金额，什么都不做是唯一的一个方案！dp[…][0] = 1；
  最终返回什么：return dp[n][amount]

伪代码：

int dp[N+1][amount+1]
dp[0][..] = 0
dp[..][0] = 1for i in [1..N]:for j in [1..amount]:把物品 i 装进背包,不把物品 i 装进背包
return dp[N][amount]

第三步：根据选择，思考动态转移

dp[i][j] 是「共有多少种凑法」
是只有前i“种”选择
选择：

• 如果我们不把第i种物品放入背包：不使用coins[i - 1]这种硬币，那么凑出面额j的方法数为dp[i - 1][j]
• 如果我们把第i种物品放入背包：即使用coins[i - 1]这种硬币，那么我们要关心的是如何凑出j - coins[i - 1]， 那么 dp[i][j] = dp[i][j - coin[i - 1]] 注意这里不是i - 1！而是用的同样i时的 容量更小的时候的dp[i][j - coin[i - 1]]
• 然后把选不选两种选择的方案数量！加到一起就是 总的方案数量！dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]]

Note

有的读者在这里可能会有疑问，不是说可以重复使用硬币吗？那么如果我确定「使用第 i 个面值的硬币」，我怎么确定这个面值的硬币被使用了多少枚？简单的一个 dp[i][j-coins[i-1]] 可以包含重复使用第 i 个硬币的情况吗？

对于这个问题，建议你再仔回头细阅读一下我们对 dp 数组的定义，然后把这个定义代入 dp[i][j-coins[i-1]] 看看：

若只使用前 i 个物品（可以重复使用），当背包容量为 j-coins[i-1] 时，有 dp[i][j-coins[i-1]] 种方法可以装满背包。

看到了吗，dp[i][j-coins[i-1]] 也是允许你使用第 i 个硬币的，所以说已经包含了重复使用硬币的情况

class Solution {
public:int change(int amount, vector<int>& coins) {// 定义dp[i][j]int n = coins.size();vector<vector<int>> dp(n + 1, vector<int>(amount + 1, 0));// base case：dp[][0]for (int i = 0; i <= n; i++) dp[i][0] = 1;// for (int i = 1; i <= n;i++) {int curCoin = coins[i - 1];for (int j = 1; j <= amount; j++) {if (j < curCoin) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j] + dp[i][j - curCoin];				}		}}return dp[n][amount];}
};

这道题只用到了，最近的两行状态dp！
思考如何空间压缩？如何记忆化搜索实现时间复杂度优化？

背包问题变体——494.目标和

打家劫舍

股票问题

贪心算法

数学

位操作

位操作是直接对整数的二进制位（0 或 1）进行运算的操作，是计算机底层数据处理的基础方式。它通过特定运算符对二进制位进行逻辑或移位处理，具有运算速度快（CPU 直接支持）、内存占用少等特点，广泛用于底层编程、算法优化、数据压缩等场景。

位运算核心优势：

• 效率极高：位运算直接在 CPU 层面执行，比加减乘除等运算更快。
• 节省空间：可用二进制位表示多个状态（如用 1 个字节存储 8 个布尔值）。
• 功能独特：特定问题，状态压缩、加密、奇偶判断等

常见应用场景

• 算法优化（如计算汉明重量、判断 2 的幂次方）。
• 数据加密（如异或加密）。
• 嵌入式编程（操作硬件寄存器）。
• 状态压缩（用二进制位表示多个开关状态）。

核心运算符

1. 与（&）：两个位都为 1 时，结果为 1；否则为 0。
   例：5（101） & 3（011） = 1（001）
2. 或（|）：两个位中至少有一个为 1 时，结果为 1；否则为 0。
   例：5（101） | 3（011） = 7（111）
3. 非（~）：将位 0 变为 1，1 变为 0（注意符号位处理，不同语言有差异）。
   例：~5（000…0101） = …11111010（取决于整数位数）
4. 异或（^）：两个位不同时（一个 0 一个 1），结果为 1；相同则为 0。
   例：5（101） ^ 3（011） = 6（110）
5. 左移（<<）：将二进制位向左移动指定位数，右侧补 0。
   例：5（101） << 1 = 10（1010）（相当于 ×2）
6. 右移（>>）：将二进制位向右移动指定位数，左侧补符号位（正数补 0，负数补 1）。
   例：5（101） >> 1 = 2（10）（相当于 ÷2 取整）

环形数组的位运算优化：index & (arr.length - 1)

1. 环形数组的常规实现：模运算 % 取余

环形数组需模拟 “头尾相接” 的循环遍历，常规做法是用模运算（取余运算）%计算索引：

• 当index递增时，index % arr.length可循环获取数组元素
• 示例（数组[1,2,3,4]）：
• (sizeof(arr) / sizeof(int) == 数组长度 arr.length

int arr[] = {1, 2, 3, 4};
int index = 0;
while (true) {// (sizeof(arr) / sizeof(int) == 数组长度 4cout << arr[index % (sizeof(arr) / sizeof(int))] << endl;index++;
}
// 输出：1,2,3,4,1,2,3,4,1,2,3,4...

缺点：模运算%对计算机而言是较昂贵的操作，性能较低。

2. 优化方案：&运算替代%

技巧题

补充高频题

42.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

接下来由浅入深介绍暴力解法 -> 备忘录解法 -> 双指针解法，在 O(N) 时间 O(1) 空间内解决这个问题。

解法一：暴力

简化问题的方法：

• 从问题局部开始思考
• 写出简单粗暴的解法
• 逐步优化

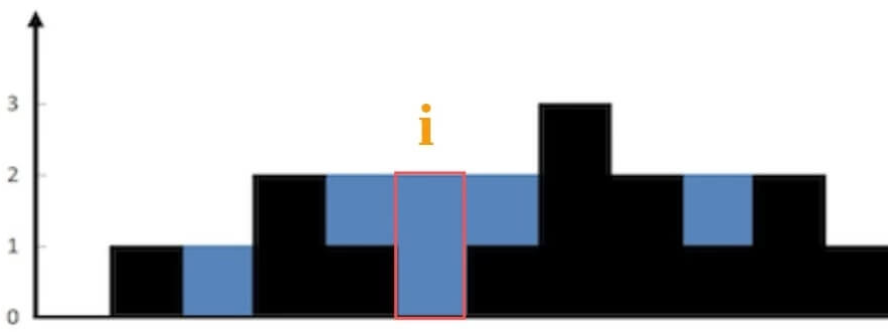
比如先放弃整体思考，而是思考某个位置i能装多少水：

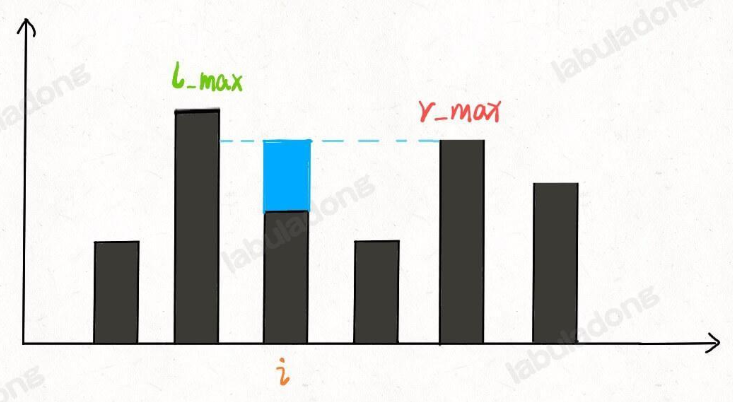
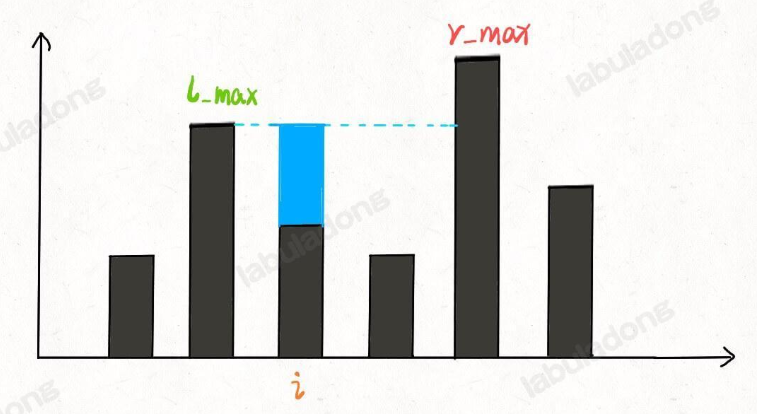
• 这个位置能装2格水，因为height[i] = 0，而水平线在高度为2的位置，2 - 0 = 2；
• 为什么水平线高度为2？
  • 取决于 min（往左边找最高的柱子高，往右边找最高的柱子）
  • 即min（max(height[0…i]),max( height[i…end])） - height[i]
    
    
    这就是本题核心思路：

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;for (int i = 1; i < n - 1;i++) {int l_max = 0;int r_max = 0;for (int j = i; j >= 0; j--) {// 往左找 l_maxl_max = max(l_max, height[j]);// }for (int j = i;) {r_max = max(r_max, height[j]);}res += min(l_max, r_max) - height[i];}return res;}
};

时间复杂度$O(N^2)$
问题出在，寻找左右两边的r_max 和 l_max 的方式非常笨拙。

注意：寻找左右最高点的时候，出发点是自身，包含自身的！如果自身就是最高，则i左右高点都是自身，后续计算res时减去自身就是0!

解法二：备忘录优化
每个位置 i 都要计算 r_max 和 l_max 吗？我们直接把每个位置需要的r_max 和 l_max结果都提前计算出来，记录下来不就行了！
将解法一中的 r_max 和 l_max 改进为 数组 r_max[i] 和 l_max[i]

• l_max[i] 表示位置 i 左边最高的柱子高度；
• r_max[i] 表示位置 i 右边最高的柱子高度

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;// 双备忘录vector<int> l_max(n);	// l_max[i] 表示 i 左边最大的柱子高vector<int> r_max(n);// 初始化备忘录l_max[0] = height[0];r_max[n - 1] = height[n - 1];// 从左向右计算l_maxfor (int i = 1; i < n; i++) {	// i 左侧最高高度，包含 i 自身l_max[i] = std::max(height[i], l_max[i - 1])}// 从右往左计算r_maxfor (int i = n - 2; i >= 0; i--) {r_max[i] = std::max(height[i], r_max[i + 1])}		// 计算答案for (int i = 1; i <= n - 2; i++) {res += std::min(l_max[i], r_max[i]) - height[i];}return res;}
};

其实思路完全就是解法一的暴力，只是避免了重复计算，算是空间换时间，时间复杂度优化到$O(N)$，但是空间复杂度也是$O(N)$。

有什么办法能优化空间复杂度？

解法三：双指针

class Solution {
public:int trap(vector<int>& height) {// 左右指针int n = height.size();int left = 0;int right = n - 1;// 定义int l_max = 0;int r_max = 0;int res = 0;while (left < right) {l_max = max(l_max, height[left]);r_max = max(r_max, height[right]);// res += min(l_max, r_max) - height[i]if (l_max < r_max) {	// 左边低res += } else {  				// 右边高 }}}};