博弈论03——混合纳什均衡的收益求法
纳什均衡第二部分
- 性别之战——回顾
- 存在纯纳什均衡
- 存在混合纳什均衡
- 总结
- payoffs收益求法
性别之战——回顾
背景:
Alice 和 Bob 这两位玩家是朋友,他们想见面喝杯咖啡。Alice 喜欢去 Costa,Bob 更喜欢去星巴克,但最重要的是,对他们来说最重要的是去同一个地方,这样他们才能真正见面。
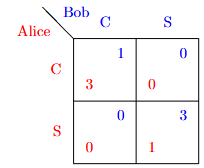
存在纯纳什均衡
Best response 法
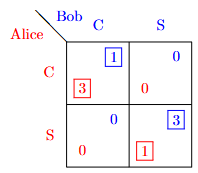
得到两个纯纳什均衡。
存在混合纳什均衡
对于Alice:
EUBC=EUBSσAC(1)+(1−σAC)(0)=σAC(0)+(1−σAC)(3)σAC=3−3σAC4σAC=3σAC=34\begin{aligned} \text{EU}_{BC} &= \text{EU}_{BS} \\ \sigma_{AC}(1) + (1 - \sigma_{AC})(0) &= \sigma_{AC}(0) + (1 - \sigma_{AC})(3) \\ \sigma_{AC} &= 3 - 3\sigma_{AC} \\ 4\sigma_{AC}&=3 \\ \sigma_{AC} &= \frac{3}{4} \end{aligned} EUBCσAC(1)+(1−σAC)(0)σAC4σACσAC=EUBS=σAC(0)+(1−σAC)(3)=3−3σAC=3=43
Alice的混合策略是(3/4 ,1/4)
对于Bob:
EUAC=EUASσBC(3)+(1−σBC)(0)=σBC(0)+(1−σBC)(1)3σBC=1−σBC4σBC=1σBC=14\begin{aligned} \text{EU}_{AC} &= \text{EU}_{AS} \\ \sigma_{BC}(3) + (1 - \sigma_{BC})(0) &= \sigma_{BC}(0) + (1 - \sigma_{BC})(1) \\ 3\sigma_{BC} &= 1 - \sigma_{BC} \\ 4\sigma_{BC}&=1 \\ \sigma_{BC} &= \frac{1}{4} \end{aligned} EUACσBC(3)+(1−σBC)(0)3σBC4σBCσBC=EUAS=σBC(0)+(1−σBC)(1)=1−σBC=1=41
Bob的混合策略是(1/4 ,3/4)
总结
混合策略的求法:设定自己的概率,让对方无差别,用对方的payoff×自己的概率,并相等。
一个博弈是否可以同时存在纯纳什均衡和混合纳什均衡?
是的,可以同时存在。
许多博弈(如“性别之战”)既有纯策略纳什均衡,也有混合策略纳什均衡。
一个博弈是否一定存在至少一种纳什均衡?
是的,每个有限博弈(有限个玩家 + 有限个策略)根据纳什定理(Nash’s Theorem),至少存在一个纳什均衡(可能是纯的,也可能是混合的)
payoffs收益求法
计算方法:
- 求出每个玩家的混合纳什策略概率;
- 相乘,求出每个事件发生的概率;
- 每个事件发生的概率乘以这个事件发生对这个玩家的payoff影响。相加求和。
性别之战
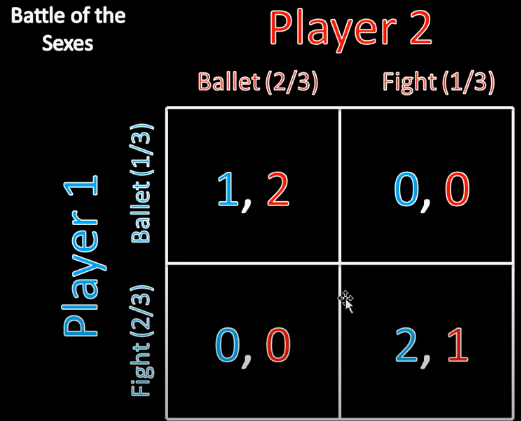
相乘,求事件概率

对于玩家1,
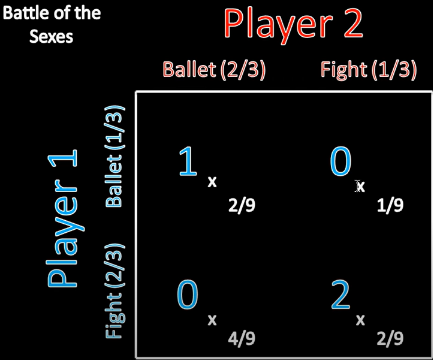
Payoff1=1∗2/9+0∗1/9+0∗4/9+2∗2/9=5/9Payoff_1 = 1 * 2/9 + 0 * 1/9 + 0 * 4/9 + 2 * 2/9 = 5/9Payoff1=1∗2/9+0∗1/9+0∗4/9+2∗2/9=5/9
对于玩家2,

Payoff2=2∗2/9+0∗1/9+0∗4/9+1∗2/9=2/3Payoff_2 = 2 * 2/9 + 0 * 1/9 + 0 * 4/9 + 1 * 2/9 = 2/3Payoff2=2∗2/9+0∗1/9+0∗4/9+1∗2/9=2/3
