当前位置：首页 > news >正文

nfls dp 刷题题解

news 2025/7/27 14:35:59

1.#3003 LCIS / 洛谷 P10954 LCIS

题意

给定两个序列，求二者的最长上升公共子序列（LCIS）。

长度为 $n$ 的序列 ${A_n\}$ 和长度为 $m$ 的序列 ${b_m\}$ ，存在 $1≤i1<i2<...<in≤m1\le i_1<i_2<...<i_n\le m$ ，使对所有 $1≤j≤n1\le j\le n$ ，都有 $a_j=b_{i,j}$ ， $∀aj<aj+1\forall a_j<a_{j+1}$ 。

$1≤n,m≤50001\le n,m\le 5000$ 。

思路

这个范围支持 $O (mn)$ 做。设 $f_i$ 表示存在以 $b_i$ 为结尾的最长 LCIS 长度。

考虑固定枚举一个 $a_i$ ，看有没有 $a_i=b_j$ ， $fj=max⁡k<j,bk<ai{fk}+1\displaystyle f_j=\max_{k<j,b_k<a_i}\{f_k\}+1$ ，其中 $max⁡\max$ 可以在 $a_i>b_j$ 时维护最大值，因为此时 $j$ 可以成为之后可能出现的 $a_i=b_{j'}$ 的 LCS 前继。

答案就是 $max f_i$ 。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5009;
ll n,m;
ll a[N],b[N];
ll f[N];
int main()
{
//	freopen("lcis.in","r",stdin);  
//	freopen("lcis.out","w",stdout);scanf("%lld",&n);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);scanf("%lld",&m);for(int i=1;i<=m;i++)scanf("%lld",&b[i]);for(int i=1;i<=n;i++){ll ma=0;for(int j=1;j<=m;j++){if(a[i]==b[j])f[j]=max(f[j],ma+1);if(a[i]>b[j])ma=max(ma,f[j]);}}ll ans=0;for(int i=1;i<=m;i++)ans=max(ans,f[i]);printf("%lld",ans);return 0;
}

2.#15952 变化序列 / AT_abc253_e Distance Sequence

题意

有多少个长度为 $N$ 的整数数列 $A=(A1,…,AN)A=(A_1,\ldots,A_N)$ 满足以下所有条件？

$\leq A_i \leq M$ ，其中 $\leq i \leq N$ 。
$∣Ai−Ai+1∣≥K|A_i - A_{i+1}| \geq K$ ，其中 $\leq i \leq N-1$ 。

请注意，答案可能非常大，请输出答案对 $998244353$ 取模后的结果。

$\leq N \leq 1000$ ， $\leq M \leq 5000$ ， $\leq K \leq M-1$ 。

思路

设 $f_{i,j}$ 表示选定了前 $i$ 个数，最后一个数是 $j$ 。那么：
$fi,j=(∑s=1j−kfi−1,s)+(∑t=j+kmfi−1,t)f_{i,j}=\left( \sum_{s=1}^{j-k}f_{i-1,s} \right)+\left( \sum_{t=j+k}^{m}f_{i-1,t} \right)$

初始化 $f_{1,i}=1$ 。对于两大坨求和符号直接前缀和优化掉就好了：设 $si,j=∑t=1jfi,ts_{i,j}=\sum_{t=1}^jf_{i,t}$ 。处理出不贡献的区间 $[l, r]$ ，其中 $l=max⁡(j−k+1,1)l=\max(j-k+1,1)$ ， $r=min⁡(j+k−1,m)r=\min(j+k-1,m)$ 。那么 $f_{i,j}=s_{i-1,m}-(s_{i-1,r}-s_{i-1,l})$ ，同时更新 $s$ 数组即可。

注意勤取模，然后就是 nfls 的空间给的很阴间，滚动数组优化即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1005,M=5009,mod=998244353;
ll n,m,k;
ll f[N][M],s[N][M];
//f(i,j):选了i个数，最后一个数是j
//s(i,j):\sum f(i,1~j) 
int main()
{scanf("%lld%lld%lld",&n,&m,&k);for(int i=1;i<=m;i++)f[1][i]=1,s[1][i]=(s[1][i-1]+1)%mod;for(int i=2;i<=n;i++){ll now=i&1,las=now^1;for(int j=1;j<=m;j++){ll l=max(j-k+1,1ll),r=min(j+k-1,m);ll minus=(l<=r?(s[las][r]-s[las][l-1]+mod)%mod:0);f[now][j]=(s[las][m]-minus+mod)%mod;s[now][j]=(s[now][j-1]+f[now][j])%mod;}}ll ans=0;for(int i=1;i<=m;i++)ans=(ans+f[n&1][i])%mod;printf("%lld",ans);return 0;
}

3.#4541 龙珠 / HDU4362 Dragon Ball

题意

肖恩得到了一张藏宝图，上面标明了龙珠出现的时间和地点。在每个时间段，会有一些龙珠出现在一条直线上，且它们同时出现。一旦肖恩拿到其中一颗龙珠，其他龙珠就会消失，因此他在每个时间段只能且必须拿到一颗龙珠。挖掘一颗龙珠会消耗他一定的能量。此外，当肖恩从位置 $x$ 移动到位置 $y$ 时，他会消耗 $∣ x - y ∣$ 的能量。假设肖恩有足够的时间去拿每个时间段里他想拿的任何一颗龙珠，我们想知道肖恩拿到所有时间段的龙珠所消耗的最小能量是多少。

给定 $m$ 个时间段，每个时间段都有 $n$ 个龙珠，给定每个龙珠的位置 $p os$ 和挖掘龙珠所消耗的能量 $cos t$ ，肖恩初始位置在 $x$ 处。

$1≤m≤501\le m\le 50$ ， $1≤n≤10001\le n\le 1000$ 。

思路

设 $f_{i,j}$ 表示在第 $i$ 时段拿龙珠 $j$ 的最小花费。那么：
$f_{i,j}=\min\{f_{i-1,k}+|pos_{i-1,k}-pos_{i,j}|\}+cost_{i,j}$

初始化 $f_{1,j}=|x-pos_{1,j}|+cost_{1,j}$ 。

这个绝对值比较难搞，不妨直接分类讨论：将每个时间段的龙珠按照 $p os$ 排序，讨论 $k$ 和 $j$ 的 $p os$ 的大小关系：

$pos_{i-1,k}>pos_{i,j}$ ： $f_{i,j}=\min\{f_{i-1,k}+pos_{i-1,k}\}-pos_{i,j}+cost_{i,j}$ ；
$pos_{i-1,k}<pos_{i,j}$ ： $f_{i,j}=\min\{f_{i-1,k}-pos_{i-1,k}\}+pos_{i,j}+cost_{i,j}$ 。

因为 $j$ 是从 $1$ 到 $n$ 平推过去更新 $k$ 的，所以满足单调性质。开一个单调指针，分别从尾和头找最优决策点 $k$ 。

最后答案是 $min f_{m,j}$ 。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll M=52,N=1009,inf=3e14;
ll T;
struct node
{ll pos,cost;
}a[M][N];
bool cmp(node x,node y)
{return x.pos<y.pos;
}
ll f[M][N];
int main()
{scanf("%lld",&T);while(T--){ll m,n,x;scanf("%lld%lld%lld",&m,&n,&x);for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)scanf("%lld",&a[i][j].pos);for(int i=1;i<=m;i++){for(int j=1;j<=n;j++)scanf("%lld",&a[i][j].cost);sort(a[i]+1,a[i]+n+1,cmp);}/*	for(int i=1;i<=m;i++){for(int j=1;j<=n;j++)printf("(%lld,%lld) ",a[i][j].pos,a[i][j].cost);cout<<endl;}*/for(int j=1;j<=n;j++)f[1][j]=abs(x-a[1][j].pos)+a[1][j].cost;for(int i=2;i<=m;i++){ll k=1;ll mi=inf;for(int j=1;j<=n;j++){while(k<=n&&a[i][j].pos>=a[i-1][k].pos){mi=min(mi,f[i-1][k]-a[i-1][k].pos);k++;}f[i][j]=mi+a[i][j].pos+a[i][j].cost;}k=n;mi=inf;for(int j=n;j>=1;j--){while(k>=1&&a[i][j].pos<=a[i-1][k].pos){mi=min(mi,f[i-1][k]+a[i-1][k].pos);k--;}f[i][j]=min(f[i][j],mi-a[i][j].pos+a[i][j].cost);}}ll ret=inf;for(int j=1;j<=n;j++)ret=min(ret,f[m][j]);printf("%lld\n",ret);}return 0;
}

4.#17125 赶集

题意

你要去赶集。有 $n$ 个村庄，举办 $m$ 次集市，按照顺序依次举行。第 $i$ 次集市在村庄 $t_i$ 举行，参加可以获得 $p_i$ 元，也可以选择不参与。

从 $i$ 村走到 $j$ 村需花费 $c×∣i−j∣c\times|i-j|$ 元。

初始时位于 $1$ 村，钱数为 $0$ ，问 $m$ 次集市举行后最大钱数。

$1≤n,m≤2×1051\le n,m\le 2\times 10^5$ ， $1≤ti≤n1\le t_i\le n$ ， $1≤c≤1091\le c\le 10^9$ ， $1≤pi≤10131\le p_i\le 10^{13}$ 。

思路

设 $f_i$ 表示举办完第 $i$ 次集市，去或者是不去的最大钱数。那么：
$fi=max⁡{fj−c×∣ti−tj∣}+pif_i=\max\{f_j-c\times|t_i-t_j|\}+p_i$

依然分类讨论拆绝对值：

$t_i>t_j$ ： $fi=max⁡{fj+c×tj}−c×ti+pif_i=\max\{f_j+c\times t_j\}-c\times t_i+p_i$ ；
$t_i<t_j$ ： $fi=max⁡{fj−c×tj}+c×ti+pif_i=\max\{f_j-c\times t_j\}+c\times t_i+p_i$ 。

可以开两棵树状数组维护两个最大值。每次获取小于 $t_i$ 的最大 $fj+c×tjf_j+c\times t_j$ 和大于 $t_i$ 的最大 $fj−c×tjf_j-c\times t_j$ 。更新完后将 $⟨ti,fi+c×tj⟩\left \langle t_i,f_i+c\times t_j \right \rangle$ 和 $⟨ti,fi+c×tj⟩\left \langle t_i,f_i+c\times t_j \right \rangle$ 分别扔上 $ti∼mt_i\sim m$ 和 $1∼ti1\sim t_i$ 的树状数组即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9,inf=3e14;
ll n,c,m;
ll f[N];//以i为结尾最大贡献 
struct BT
{ll T[2][N];void init(){for(int i=1;i<N;i++)T[0][i]=T[1][i]=-inf;}ll lowbit(ll x){return x&(-x);}void add(ll x,ll k,bool op){if(!op){for(int i=x;i<N;i+=lowbit(i))T[op][i]=max(T[op][i],k);}else {for(int i=x;i>=1;i-=lowbit(i))T[op][i]=max(T[op][i],k);}}ll query(ll x,bool op){ll ret=-inf;if(!op){for(int i=x;i>=1;i-=lowbit(i))ret=max(ret,T[op][i]);}else {for(int i=x;i<N;i+=lowbit(i))ret=max(ret,T[op][i]);}return ret;}
}B;
int main()
{scanf("%lld%lld%lld",&n,&c,&m);B.init();B.add(1,c,0);B.add(1,-c,1);//初始化f(1)=c+0; for(int i=1;i<=m;i++){ll t,p;scanf("%lld%lld",&t,&p);ll m1=B.query(t,0),m2=B.query(t,1);//0找<t 1找>t f[i]=max(m1-c*t,m2+c*t)+p;B.add(t,f[i]+c*t,0);B.add(t,f[i]-c*t,1);}ll ans=0;for(int i=1;i<=m;i++)ans=max(ans,f[i]);printf("%lld",ans); return 0;
}

5.#24108 图上 LIS / CF960F Pathwalks

题意

给定 $n$ 个点 $m$ 条边的有向图，可能不连通，可能有重边，也可能会有自环。求最长的路径(可以经过重复节点)，使得这条路径的编号和权值都严格单调递增，其中编号指输入的顺序。路径的长度是指经过边的数量。

$1≤n,m≤1051\leq n,m\leq10^5$ ， $0≤wi≤1050\le w_i\le10^5$ 。

思路

设 $f_{u,w}$ 表示以 $u$ 节点结尾，最后一次边权为 $w$ 的最长路径长度。那么在有向边 $w(u→v)w(u\rightarrow v)$ 上转移：
$f_{v,w}=\max\{f_{u,w'}+1\}(w'<w,u<v)$

可以用 map 维护边权 $f_{u,w}$ 的第一关键字 $w$ 和第二关键字 dp 值本身。在 $mp_u$ 的第一关键字二分查找 $w$ ，对应指针 $i t$ ， $i t - 1$ 的权值就是第二关键字。那么第一第二关键字的单调性都要维护。

（有点口胡了，杂记么，具体细节见代码）

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
map<int,int>dp[N];
int find(int u,int x)
{auto it=dp[u].lower_bound(x);return it==dp[u].begin()?0:(--it)->second;
}
int n,m,ans=0;
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v,k;scanf("%d%d%d",&u,&v,&k);int res=find(u,k)+1; if(res>find(v,k)){auto it=dp[v].lower_bound(k);dp[v][k]=res;while(it!=dp[v].end()&&it->second<=res) dp[v].erase(it++);}ans=max(ans,res);}printf("%d",ans);return 0;
}

6.#8518 杰瑞征途 / 洛谷 P4072 征途

题意

Pine 开始了从 $S$ 地到 $T$ 地的征途。从 $S$ 地到 $T$ 地的路可以划分成 $n$ 段，相邻两段路的分界点设有休息站。Pine 计划用 $m$ 天到达 $T$ 地。除第 $m$ 天外，每一天晚上 Pine 都必须在休息站过夜。所以，一段路必须在同一天中走完。

Pine 希望每一天走的路长度尽可能相近，所以他希望每一天走的路的长度的方差尽可能小。帮助 Pine 求出最小方差是多少。

设方差是 $v$ ，可以证明， $v×m2v\times m^2$ 是一个整数。为了避免精度误差，输出结果时输出 $v×m2v\times m^2$ 。

$\le n \le 3000$ ，保证从 $S$ 到 $T$ 的总路程不超过 $3×1043\times 10^4$ ， $\leq m \leq n$ ，每段路的长度为不超过 $\times 10^4$ 的正整数。

思路

先转化一下方差： $s2=−(∑i=1mxi)2m2+∑i=1mxi2ms^2=-\dfrac{\left( \displaystyle\sum_{i=1}^m x_i\right)^2}{m^2}+\dfrac{\displaystyle\sum_{i=1}^mx_i^2}{m}$ 。乘上 $m^2$ 就是：
$−(∑i=1mxi)2+m(∑i=1mxi2)-\left( \sum_{i=1}^m x_i\right)^2+m\left(\sum_{i=1}^mx_i^2\right)$

式子左边是个定值，因此 dp 做右边。设 $f_{i,j}$ 表示第 $i$ 天走完了前 $j$ 段，每段路径和的各自平方之和的最小值，形如 $∑t=1jxt2\displaystyle\sum_{t=1}^jx_t^2$ 。不妨设 $si=∑t=1iats_i=\sum_{t=1}^ia_t$ ，有转移：
$f_{i,j}=\min\{f_{i-1,k}+(s_j-s_k)^2\}$

初始化 $f_{1,i}=s_i^2$ 。

这个转移是 $O(n^2)$ 的，可以斜率优化整一整。枚举 $i, j$ ，设 $k 1 < k 2$ 且 $k 2$ 优于 $k 1$ ：
$f_{i-1,k1}+s_j^2+s_{k1}^2-2s_js_{k1}>f_{i-1,k2}+s_j^2+s_{k2}^2-2s_js_{k2}$

$fi−1,k1−fi−1,k2+sk12−sk22sk1−sk2<2sj\frac{f_{i-1,k1}-f_{i-1,k2}+s_{k1}^2-s_{k2}^2}{s_{k1}-s_{k2}}<2s_j$

是 $slope<x_i$ 的形式，维护单调递增斜率，最优决策取队首。

记得对每个 $j$ 计算完之后，清空单调队列。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define dd double
const ll N=3005;
ll n,m;
ll a[N],s[N];
ll f[N][N],q[N];
ll _2(ll x)
{return x*x;
}
double slope(ll i,ll j1,ll j2)
{return (dd)(f[i][j1]-f[i][j2]+_2(s[j1])-_2(s[j2]))/(dd)(s[j1]-s[j2]);
}
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);s[i]=s[i-1]+a[i];}for(int i=1;i<=n;i++)f[1][i]=_2(s[i]);for(int i=2;i<=m;i++){ll hh=1,tt=0;for(int j=1;j<=n;j++){while(hh<tt&&slope(i-1,q[hh],q[hh+1])<=2*s[j])hh++;f[i][j]=f[i-1][q[hh]]+_2(s[j]-s[q[hh]]);while(hh<tt&&slope(i-1,q[tt],j)<slope(i-1,q[tt-1],q[tt]))tt--;q[++tt]=j;}}printf("%lld",m*f[m][n]-_2(s[n]));return 0;
}

7.#2576 斜率

题意

平面中有 $n$ 个点 $x_i,y_i)$ ，有 $m$ 条直线，它们的斜率 $k_j$ 已经确定。对于 $m$ 条直线需要在给定的 $n$ 个点中，选出一个点 $(x, y)$ ，使 $k x + y$ 最大。

思路

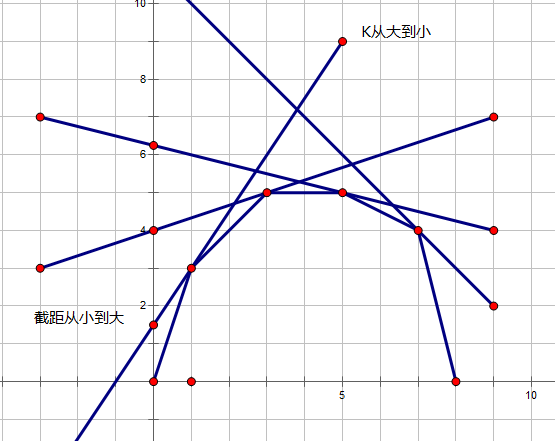
看表达式： $k x + y$ ——如果把 $k$ 取相反数，那么就是直线的表达式，求截距。那么就只要维护一个上凸包即可——因为题目中的式子，所以在图中的斜率正负是相反的，即维护斜率递减。
在这里插入图片描述

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define dd double
const ll N=1e5+9;
ll n,m;
struct point
{ll x,y;
}p[N],stk[N];
ll top;
bool cmp1(point x,point y)
{if(x.x!=y.x)return x.x<y.x;return x.y<y.y;
}
struct kk
{ll k,id;
}a[N];
bool cmp2(kk x,kk y)
{return x.k<y.k;
}
bool check(point x,point y,point z)
{return (y.y-x.y)*(z.x-y.x)<=(z.y-y.y)*(y.x-x.x);
}
ll cal(ll id,ll k)
{return k*stk[id].x+stk[id].y;
}
ll ans[N];
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){ll x,y;scanf("%lld%lld",&x,&y);p[i]=(point){x,y};}for(int i=1;i<=m;i++){ll k;scanf("%lld",&k);a[i]=(kk){k,i};}sort(p+1,p+n+1,cmp1);sort(a+1,a+m+1,cmp2);stk[++top]=p[1];stk[++top]=p[2];for(int i=3;i<=n;i++){while(top>1&&check(stk[top-1],stk[top],p[i]))top--;stk[++top]=p[i];}ll pos=1;for(int i=1;i<=m;i++){while(pos<top&&cal(pos,a[i].k)<=cal(pos+1,a[i].k))pos++;ans[a[i].id]=cal(pos,a[i].k);}for(int i=1;i<=m;i++)printf("%lld\n",ans[i]); return 0;
}

8.#3074 米仓 / 洛谷 P5844 IOI2011 Ricehub

题意

乡间有一条笔直而长的路称为“米道”。沿着这条米道上 $R$ 块稻田，每块稻田的坐标均为一个 $1$ 到 $L$ 之间(含 $1$ 和 $L$ )的整数。这些稻田按照坐标以不减的顺序给出，即对于 $\le i < R$ ，稻田 $i$ 的坐标 $X [i]$ 满足 $\le X[0] \le \cdots \le X[R-1] \le L$ 。

注意：可能有多块稻田位于同一个坐标上。

我们计划建造一个米仓用于储存尽可能多的稻米。和稻田一样，米仓将建在米道上，其坐标也是一个 $1$ 到 $L$ 之间的整数（含 $1$ 和 $L$ ）。这个米仓可以建在满足上述条件的任一个位置上，包括那些原来已有一个或多个稻田存在的位置。

在收获季节，每一块稻田刚好出产一滿货车的稻米。为了将这些稻米运到米仓，需要雇用一位货车司机来运米。司机的收费是每一满货车运送一个单位的距离收取 $1$ 元。換言之，将稻米从特定的稻田运到米仓的费用在数值上等于稻田坐标与米仓坐标之差的绝对值。

不幸的是，今年预算有限，我们至多只能花费 $B$ 元运费。你的任务是要帮我们找出一个建造米仓的位置，可以收集到尽可能多的稻米。

$\le R \le 10^5$ ， $\le L \le 10^9$ ， $\le B \le 2 \times 10^{15}$ 。

思路

对于给定 $n$ 个点让你设置一个点，使得所有点到设置点的距离之和最小这种题，已经被泛化为“小奥题”——奇数中间点，偶数中间段。证明也很好证。

我们发现这题有距离（路费）限制，我们不妨用用单调指针 $[l, r]$ 框定选了的米仓，计算下标在 $[l, r]$ 的所有稻田的最小运输费用。枚举一个固定左端点 $l_i$ ，我们发现 $r_i$ 必然符合单调的性质。

怎么计算贡献呢？根据上面的结论，发现米仓 $x$ 取在 $a_{mid}$ （ $mid=⌊l+r2⌋mid=\left\lfloor \dfrac{l+r}{2} \right\rfloor$ ）肯定是最优的。对于长度 $l e n = r - l + 1$ ，我们分奇偶讨论，设 $si=∑t=1iats_i=\displaystyle\sum_{t=1}^ia_t$ ：

$l e n$ 为偶数：此时总距离为 $x-a_l+x-a_{l+1}+...+x-a_{mid}+a_{mid+1}-x+...+a_{r-1}-x+a_r-x$ ，左右的 $+ x$ 和 $- x$ 可以抵消，答案就是 $s_r-s_{mid}-(s_{mid}-s_l)$ ；
$l e n$ 为奇数：此时总距离为 $x-a_l+x-a_{l+1}+...+x-a_{mid-1}+0+a_{mid+1}-x+...+a_{r-1}-x+a_r-x$ ，答案就是 $s_r-s_{mid}-(s_{mid-1}-s_l)$ 。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+9;
ll n,L,lim;
ll a[N],s[N];
ll cal(ll l,ll r)
{ll mid=(l+r)>>1,len=r-l+1;if(len&1)return s[r]-s[mid]-(s[mid-1]-s[l-1]);return s[r]-s[mid]-(s[mid]-s[l-1]);
}
int main()
{scanf("%lld%lld%lld",&n,&L,&lim);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);s[i]=s[i-1]+a[i];}ll r=1,ans=0;for(int l=1;l<=n;l++){while(r<n&&cal(l,r+1)<=lim)r++;if(cal(l,r)<=lim)ans=max(ans,r-l+1);}printf("%lld",ans);return 0;
}