【AcWing 143题解】最大异或对
AcWing 143. 最大异或对
【题目描述】
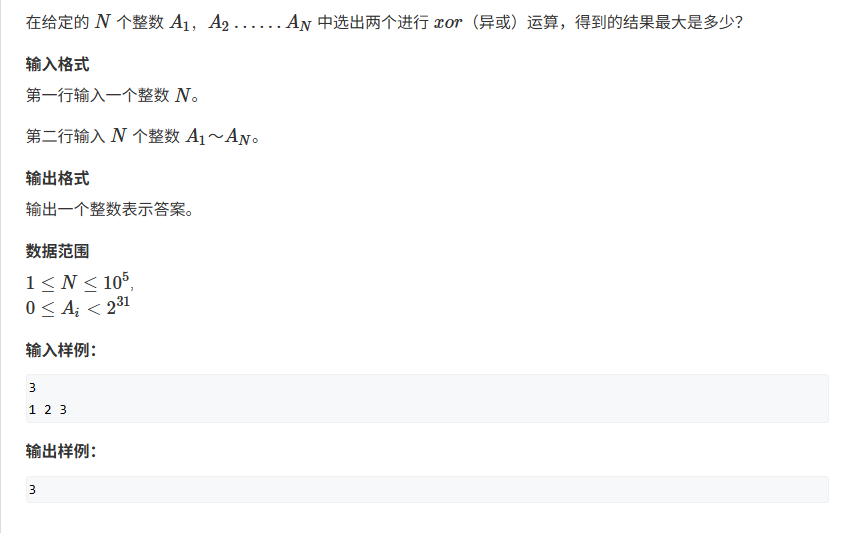
在查看解析之前,先给自己一点时间思考哦!

【题解】
本题要求给定一个整数序列,找出其中任意两个数进行异或运算后,结果的最大值是多少。由于数据规模较大,我们不能简单地通过两层循环直接遍历所有组合,这样的时间复杂度会达到O(n2)O(n^2)O(n2),超出了时间限制。
我们可以利用Trie树来高效解决这个问题。通过使用前缀树,我们能够将每个整数拆分成二进制形式,按照其二进制位插入树中,然后在查询时可以通过比较来找到最大可能的异或值。
关键点:
异或性质:我们要最大化的是两个数的异或值,而异或的性质决定了异或值越大,二者的对应位越不相同。因此,在查询时,我们会尽量选择不同的位进行匹配。
Trie 树结构:每个节点代表一个二进制位(0 或 1)。从根节点开始,每个数按位插入,如果当前数的某一位是 1,那么它就沿着该位的路径插入树中。
查询最大异或值:当我们要查询一个数的最大异或值时,从当前数的二进制表示的每一位开始,尽量沿着与当前位不同的路径走。
实现步骤:
将每个数的二进制位逐位插入到 Trie 树中。
在插入每个数的同时,查询当前数和 Trie 树中已有数的最大异或值,并更新最大异或值。
【参考代码】
#include <iostream>
using namespace std;// 最大节点数和最大Trie树的容量
const int N = 1e5 + 10, M = 31 * N;
// son[i][0/1] 表示节点 i 的左/右子节点,a 存储输入的数,idx 用来给每个节点编号
int son[M][2], a[N], idx; // 插入一个数到 Trie 树
void insert(int x) {int p = 0;// 从高位到低位插入数的二进制位for(int i = 30; i >= 0; i--) {int u = x >> i & 1; // 获取当前二进制位if(!son[p][u]) // 如果该路径没有节点,则创建新节点son[p][u] = ++idx;p = son[p][u]; // 移动到下一个节点}
}// 查询当前数与树中已有数的最大异或值
int query(int x) {int p = 0, res = 0; // p 为当前节点,res 为当前异或结果// 从高位到低位查询最大异或值for(int i = 30; i >= 0; i--) {int u = x >> i & 1; // 获取当前二进制位// 尝试选择与当前位不同的路径,以得到更大的异或值if(son[p][!u]) {p = son[p][!u];res = res * 2 + !u;} else {p = son[p][u];res = res * 2 + u;}}return res;
}int main() {int n;cin >> n; for(int i = 0; i < n; i++)cin >> a[i]; int res = 0; // 用来存储最大异或值for(int i = 0; i < n; i++) {insert(a[i]); // 将当前数插入到 Trie 树int t = query(a[i]); // 查询当前数的最大异或值res = max(res, a[i] ^ t); // 更新最大异或值}cout << res << endl; return 0;
}
