考研复习-数据结构-第八章-排序
排序的概念
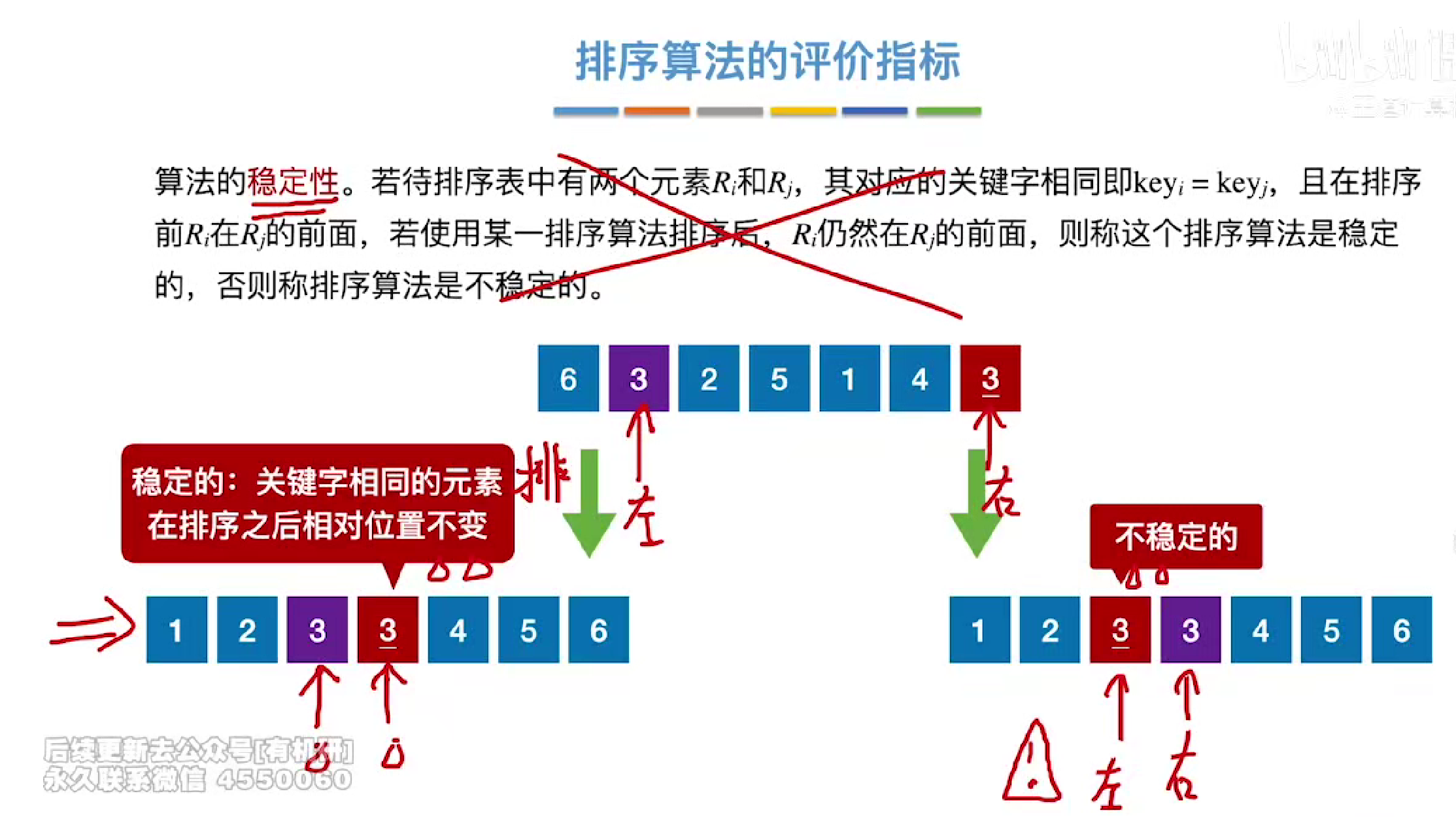
稳定性
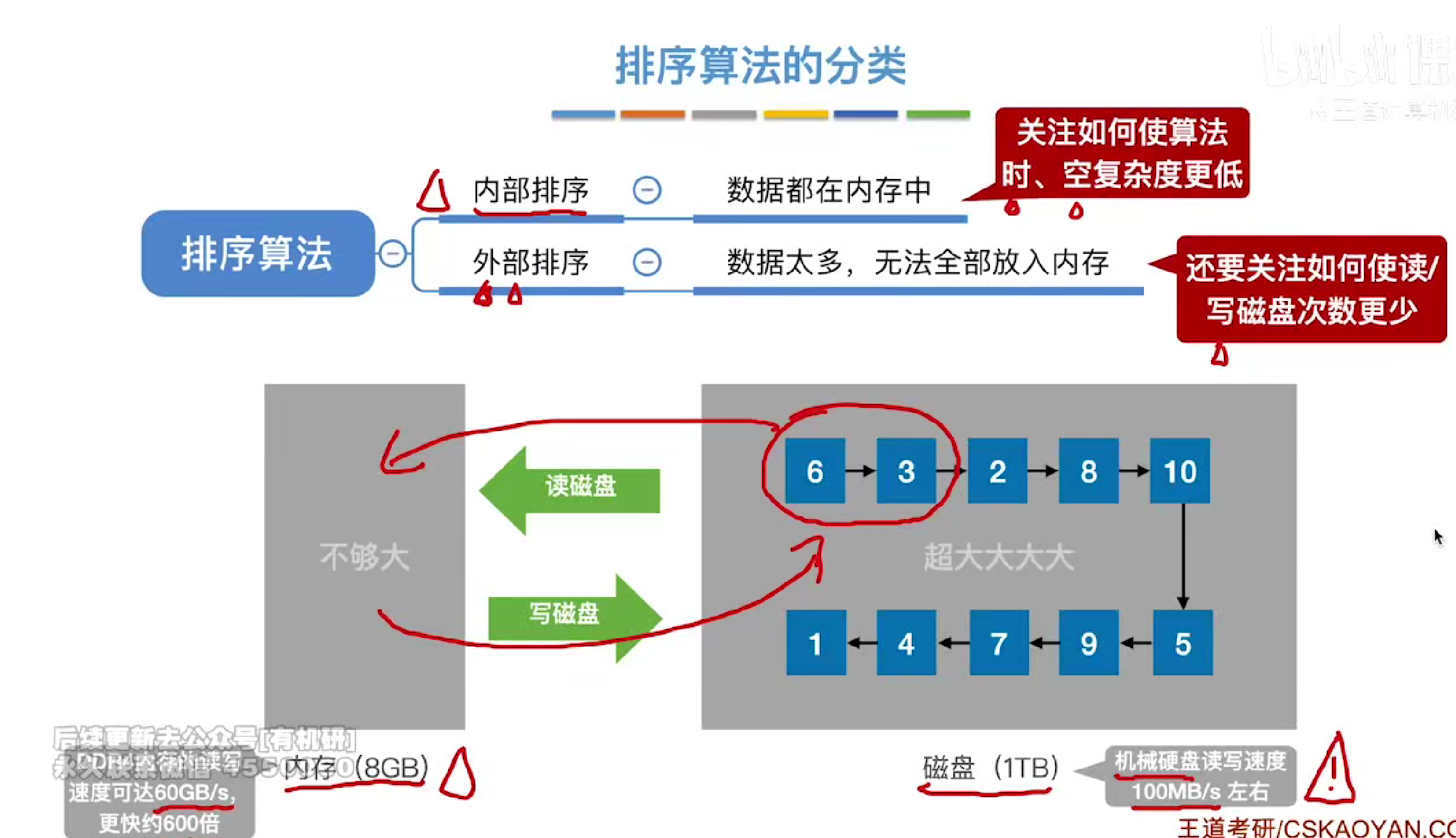
排序分类(内部外部排序)
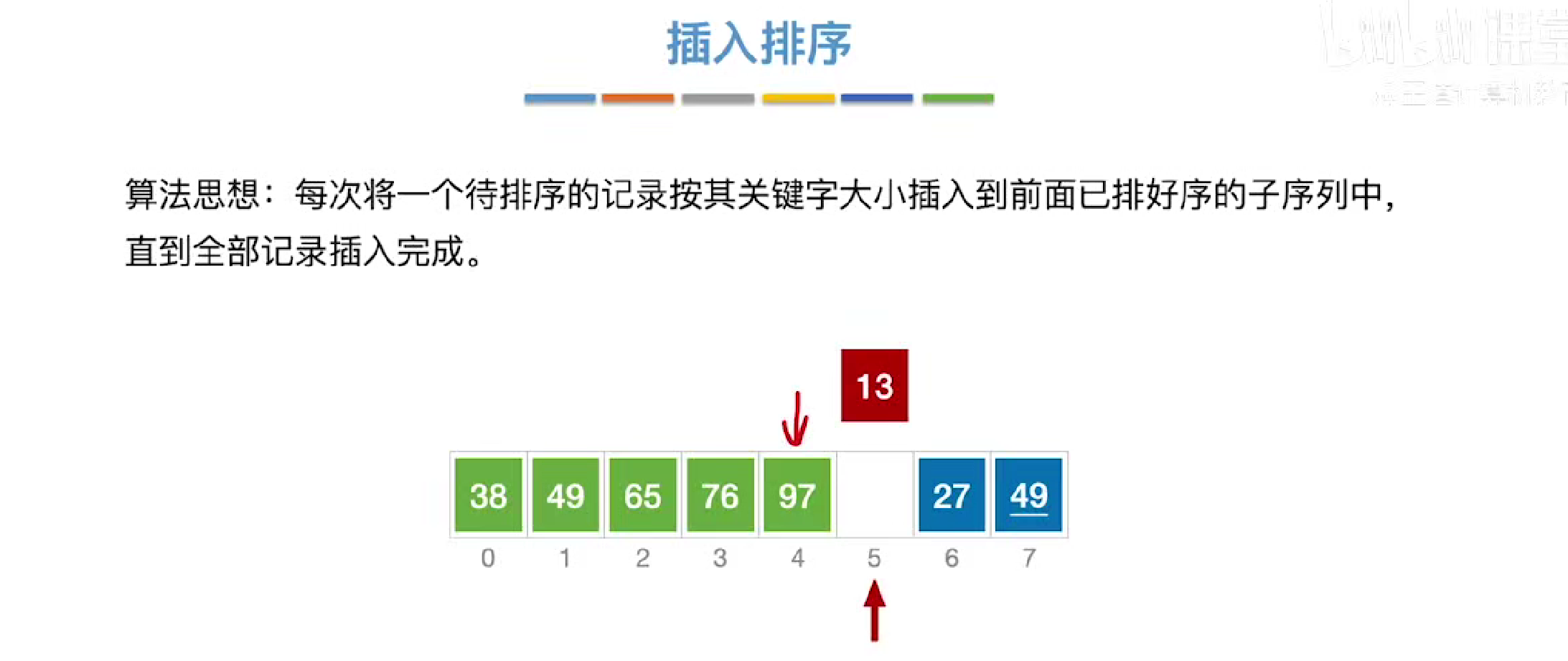
插入排序
每次都挑选一个关键字与前面排好序的关键字进行对比,他是稳定的算法
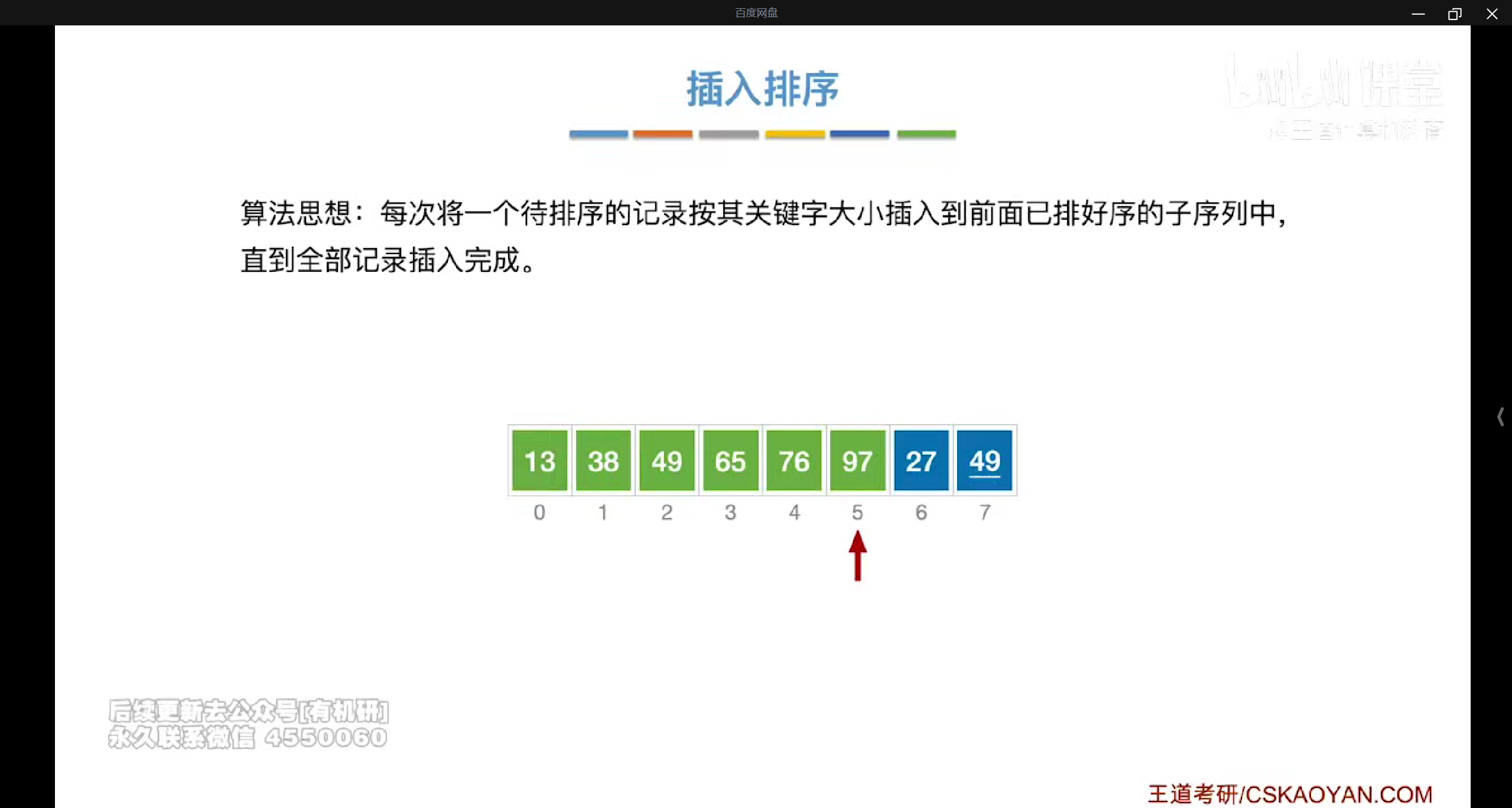
代码实现

哨兵插入实现
0号位置取代temp

时空复杂度
最好是n
最坏是n²
平均是n²
空间为o(1)量级
当插入排序基本有序的时候时间复杂度很好

优化
折半查找查找前面的插入序列
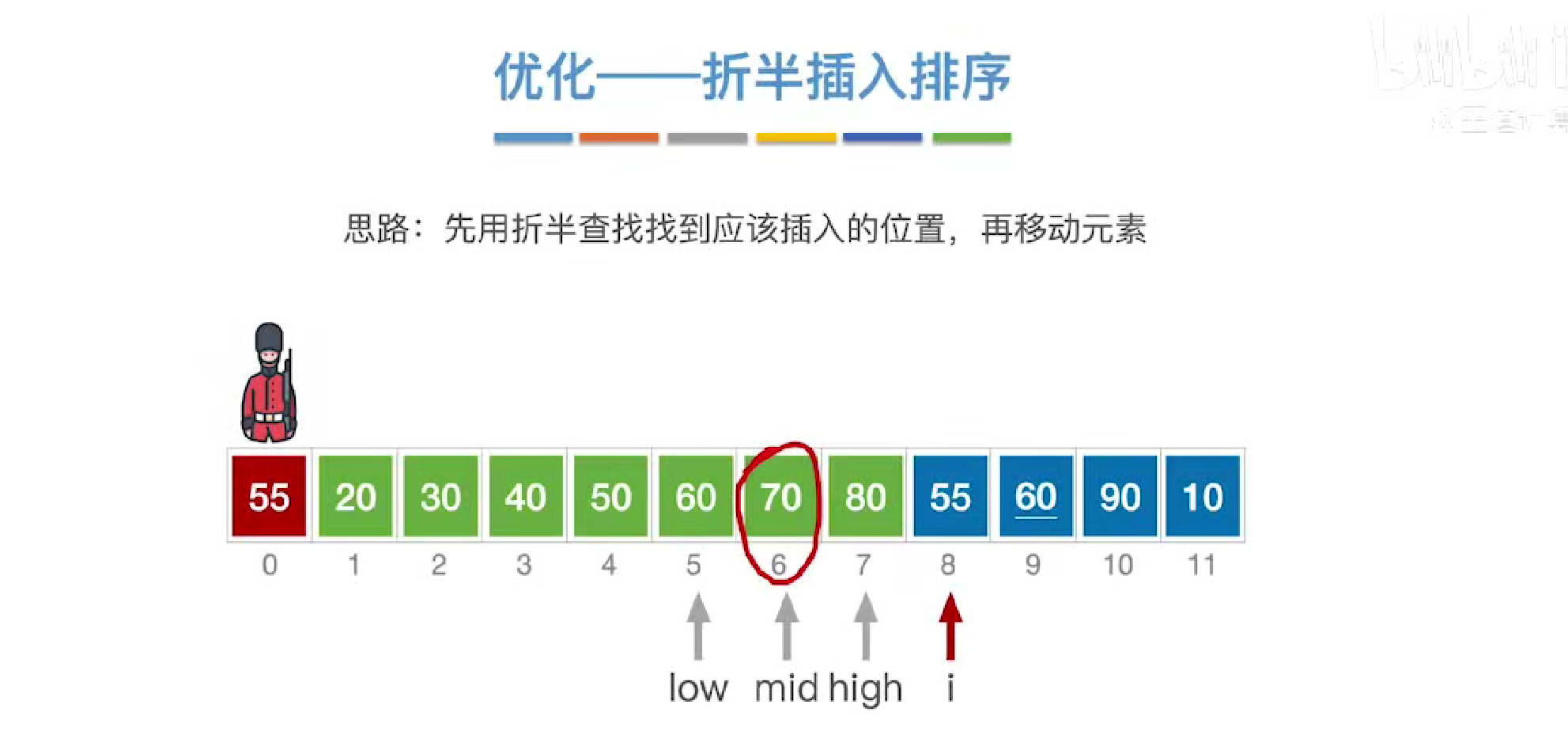
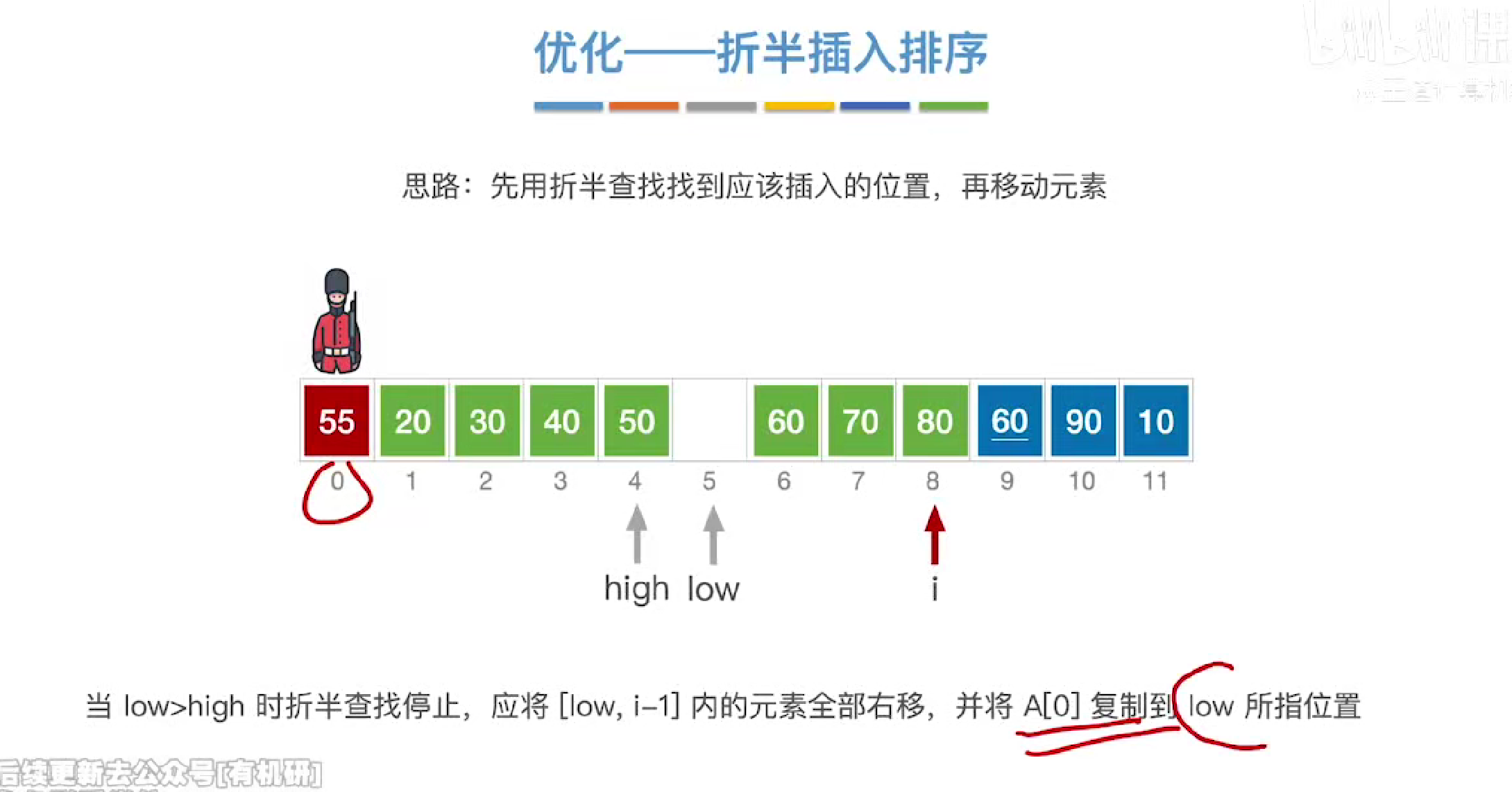
当遇到相等的元素时,我们会让low右移,保证算法的稳定性
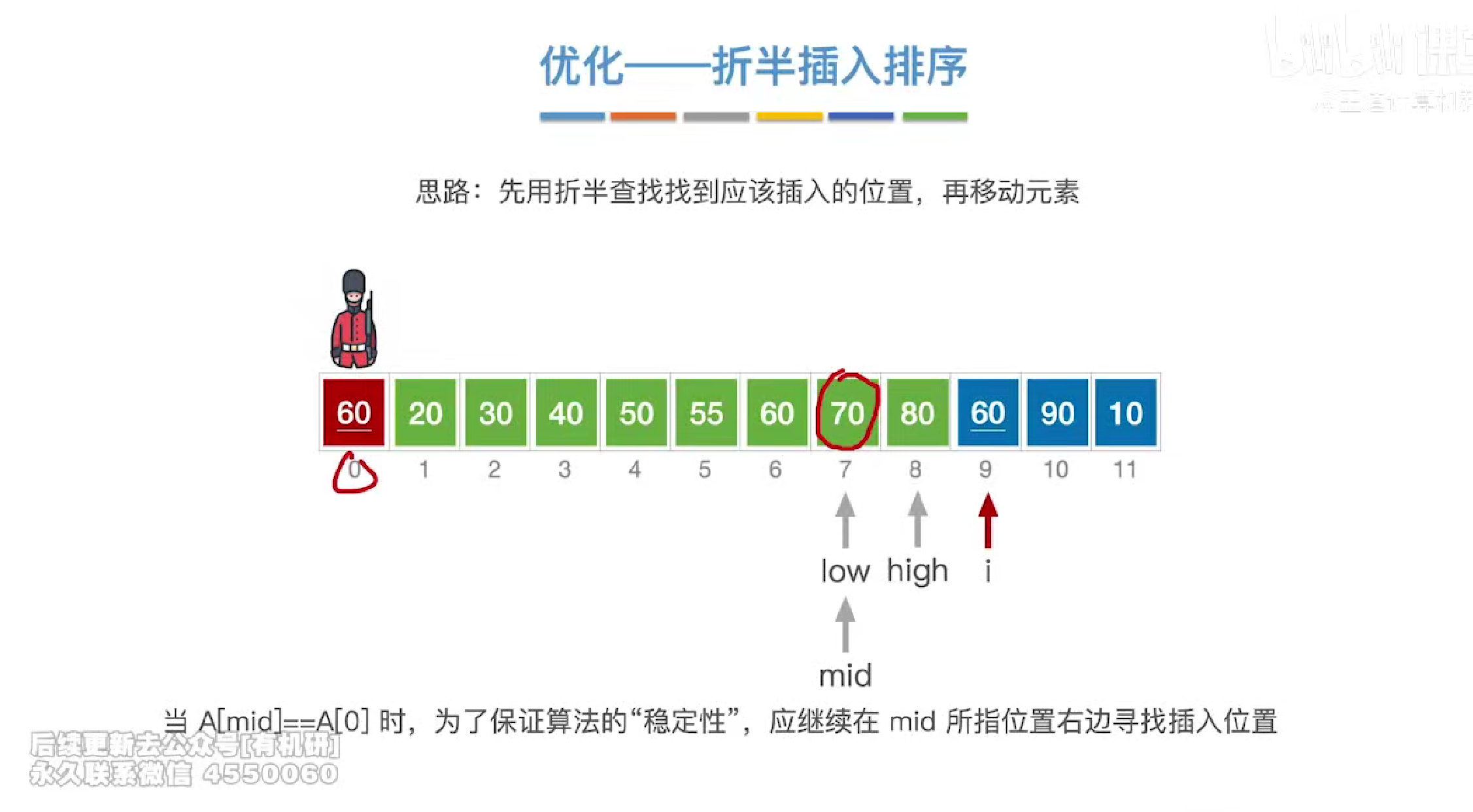
时空复杂度

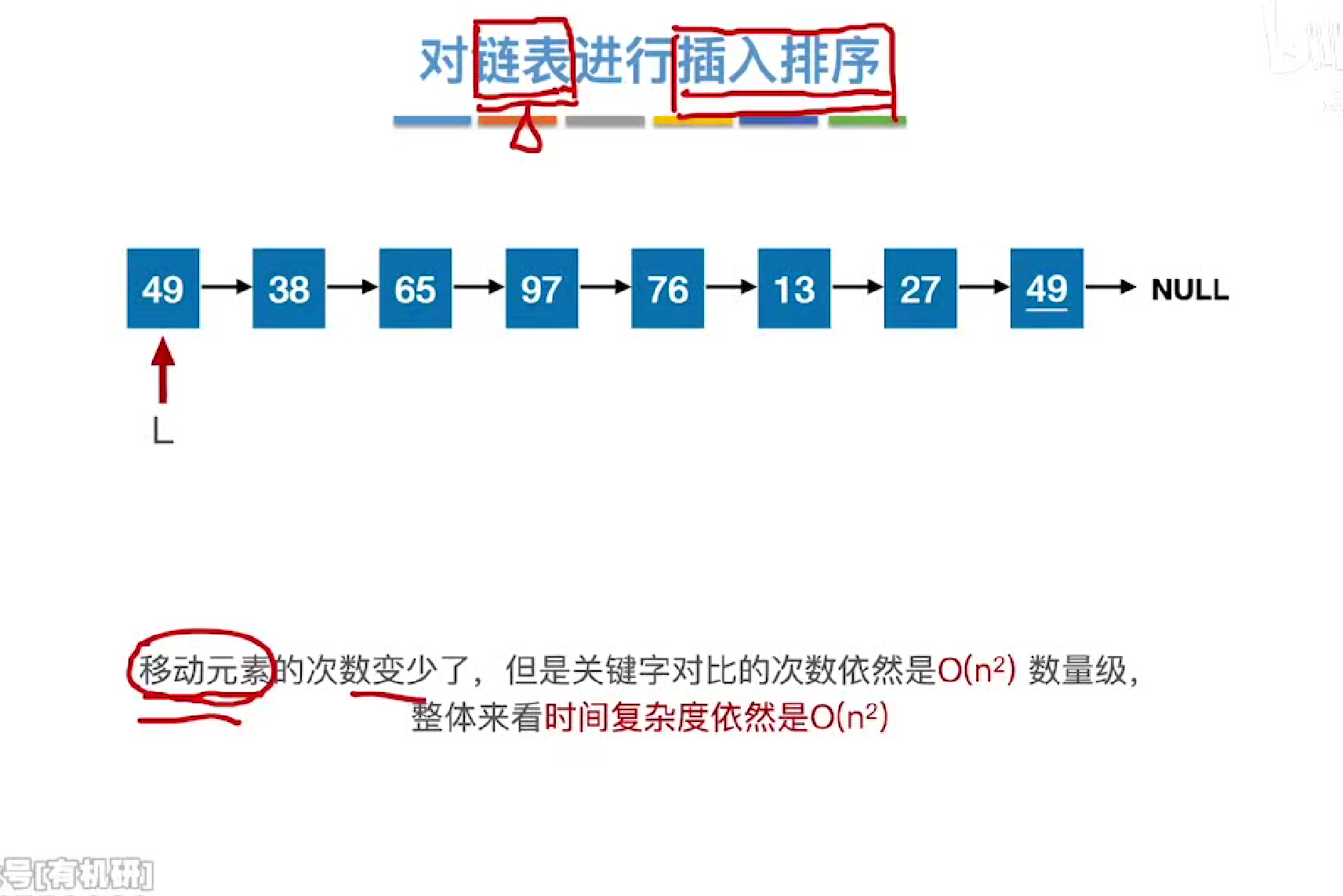
链表插入排序
希尔排序
从部分到整体
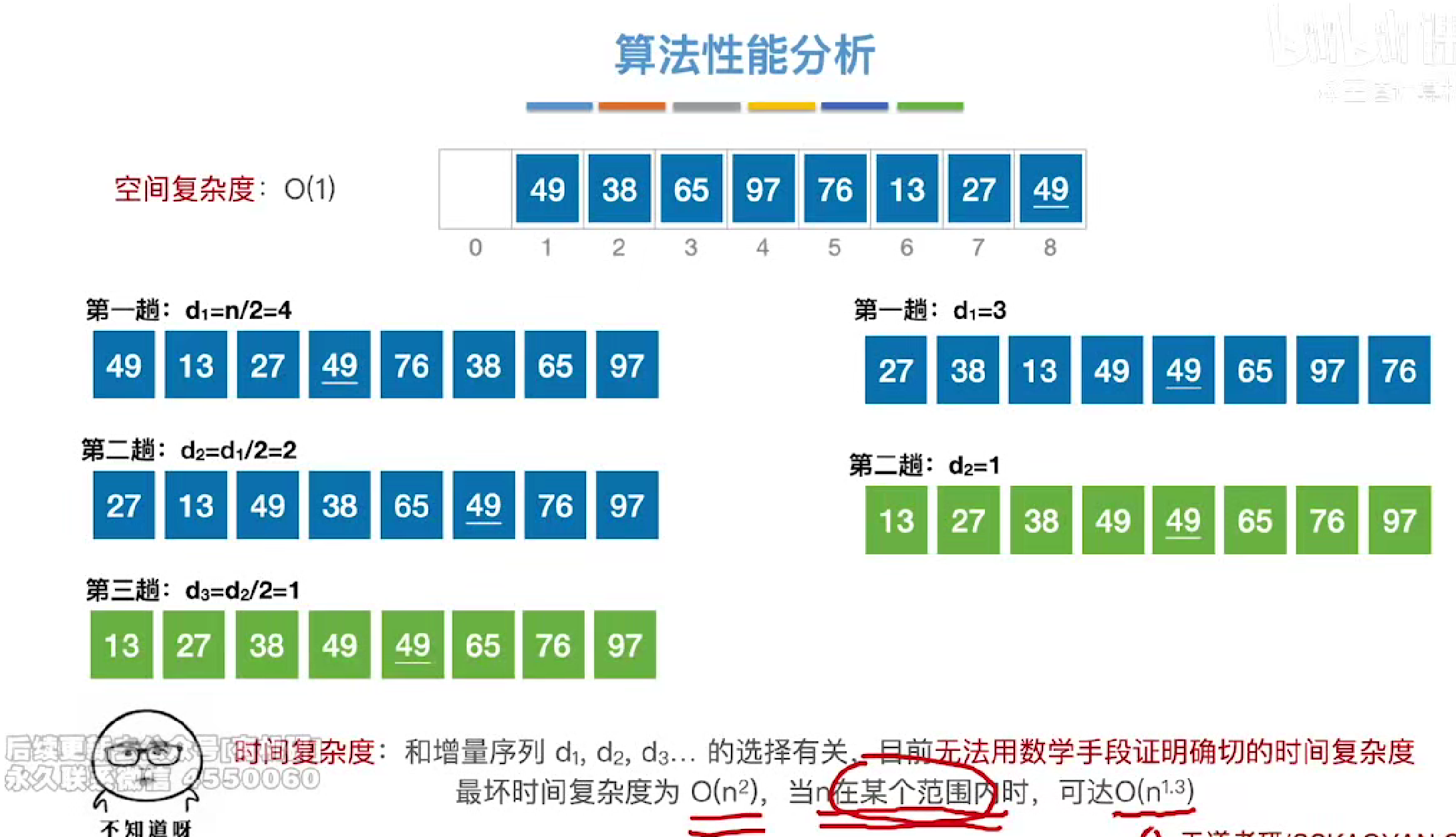
实例
第一趟
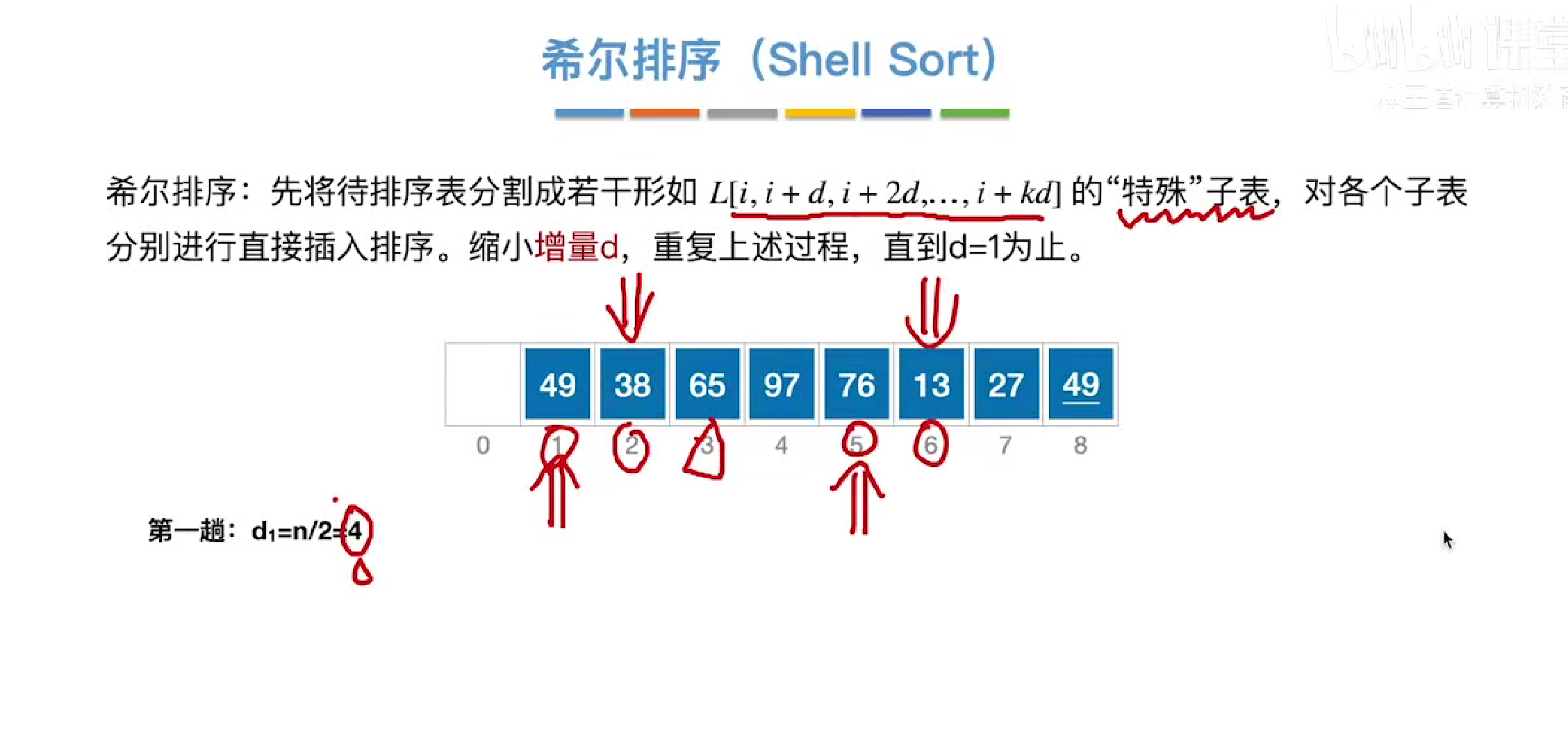
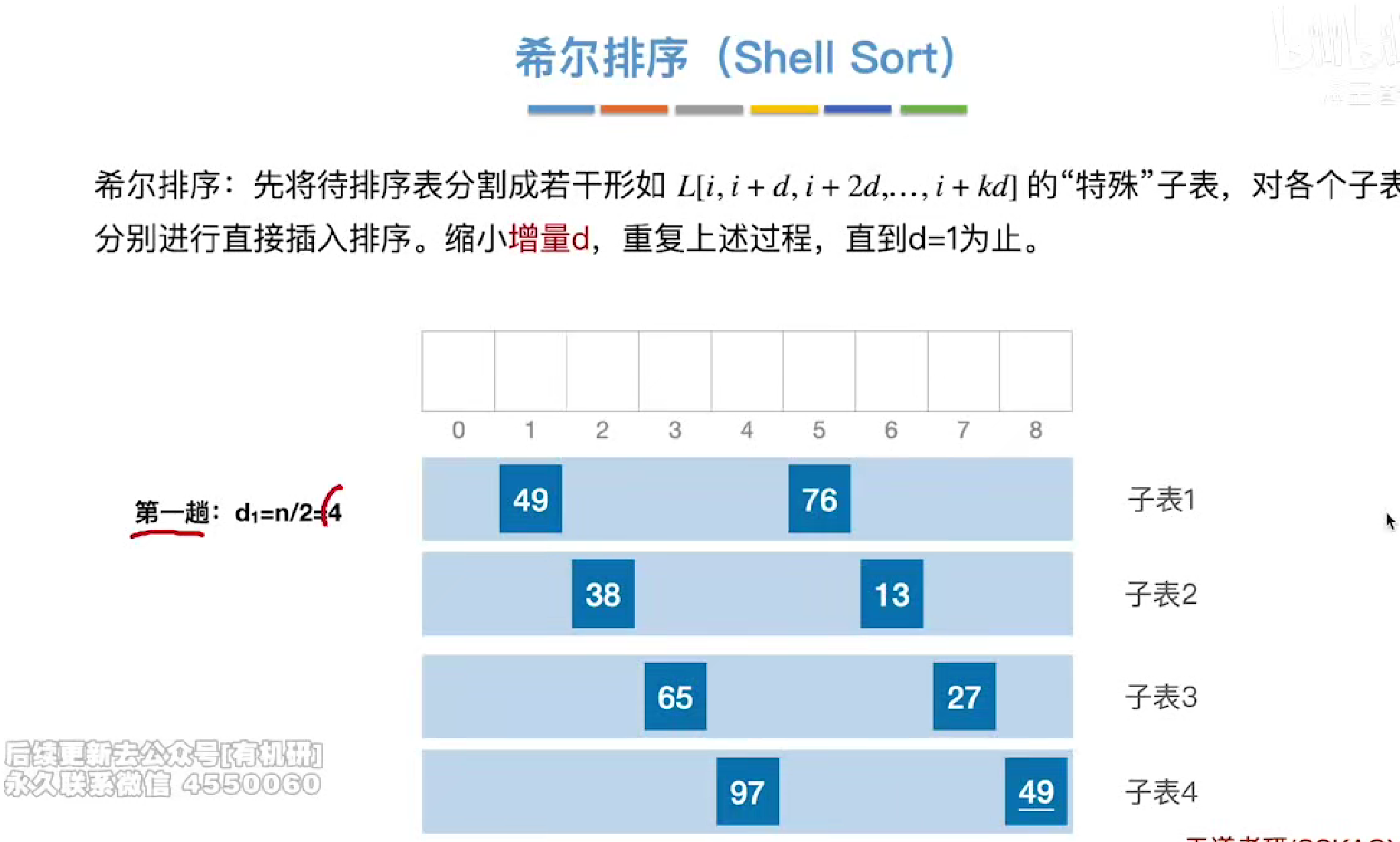
将间隔相等的元素分到一起成为一个子表
然后再子表中进行直接插入排序更改位置
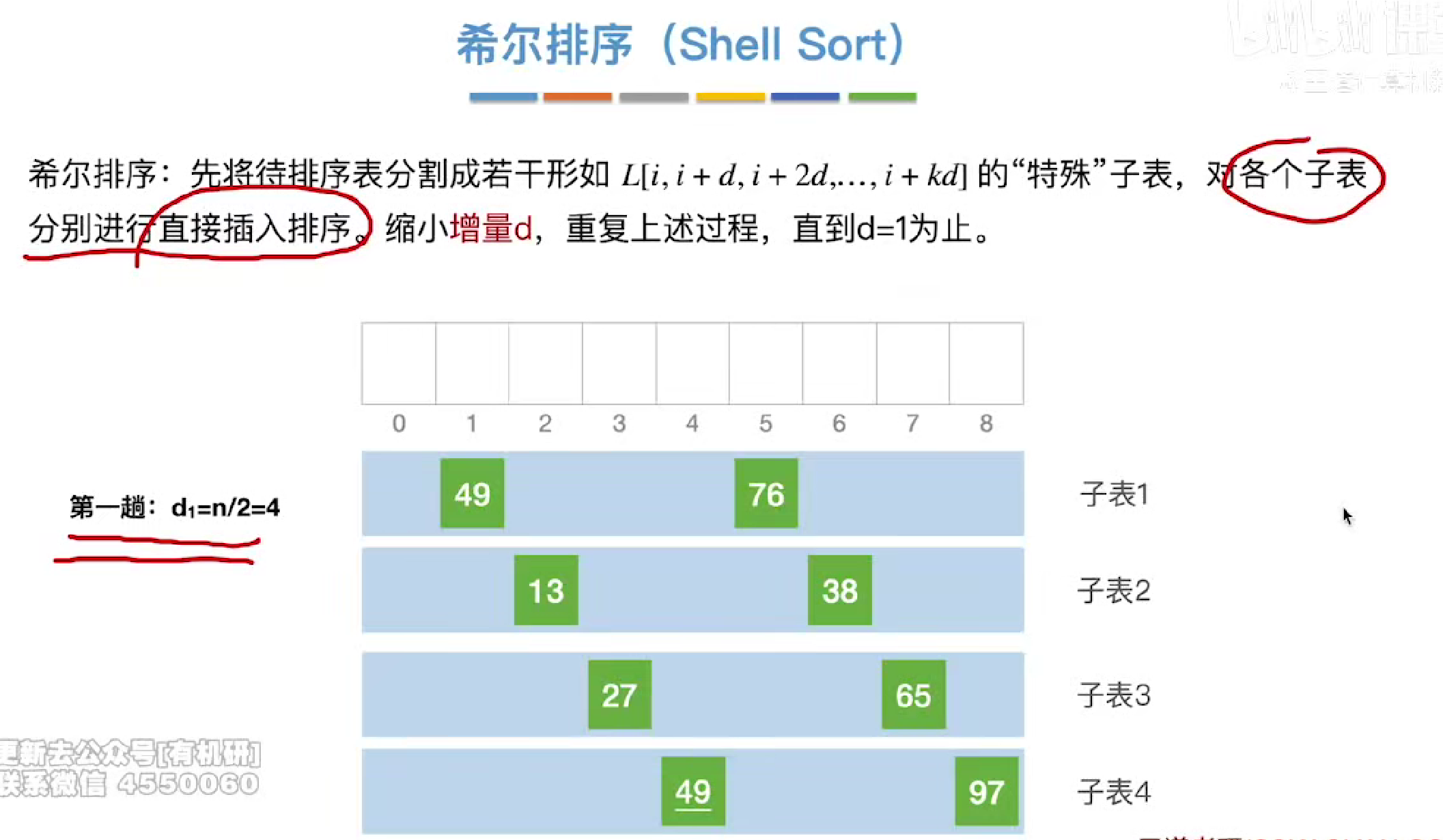
第二趟
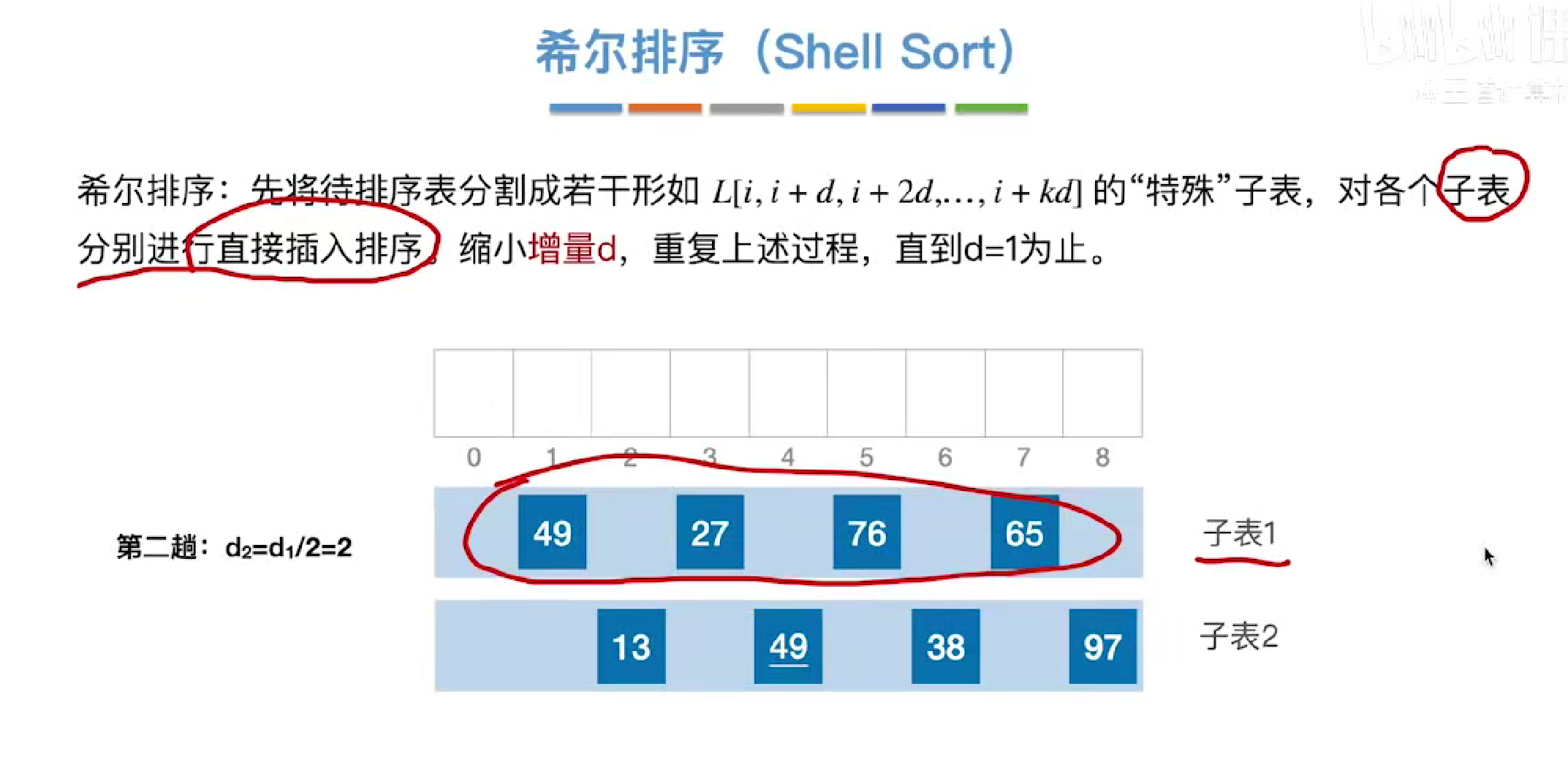
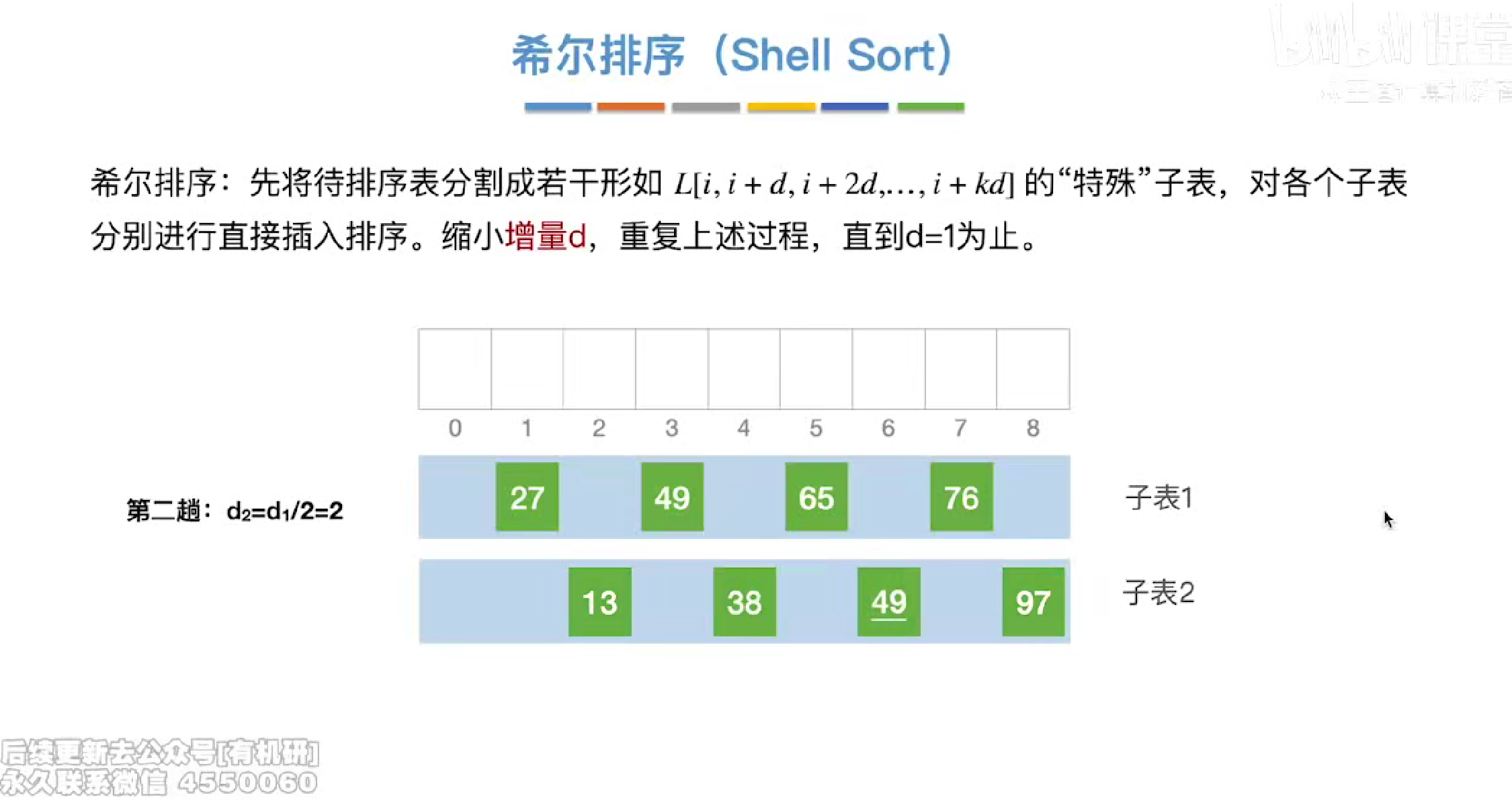
第三趟


代码实现

时空复杂度


冒泡排序
每次比对前后的两个元素如果大小不一则互换元素

每次都会选择一个最小的元素冒泡到最前面
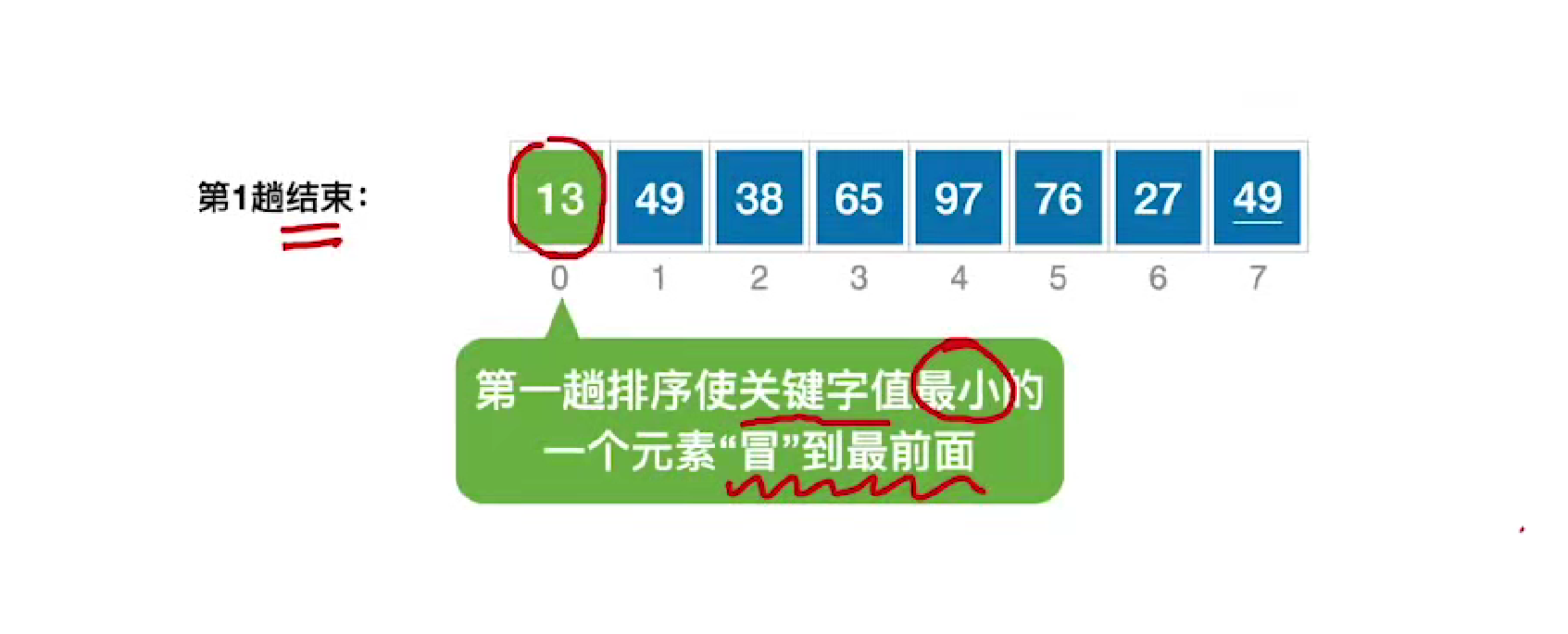
第二趟会选择一个次小的
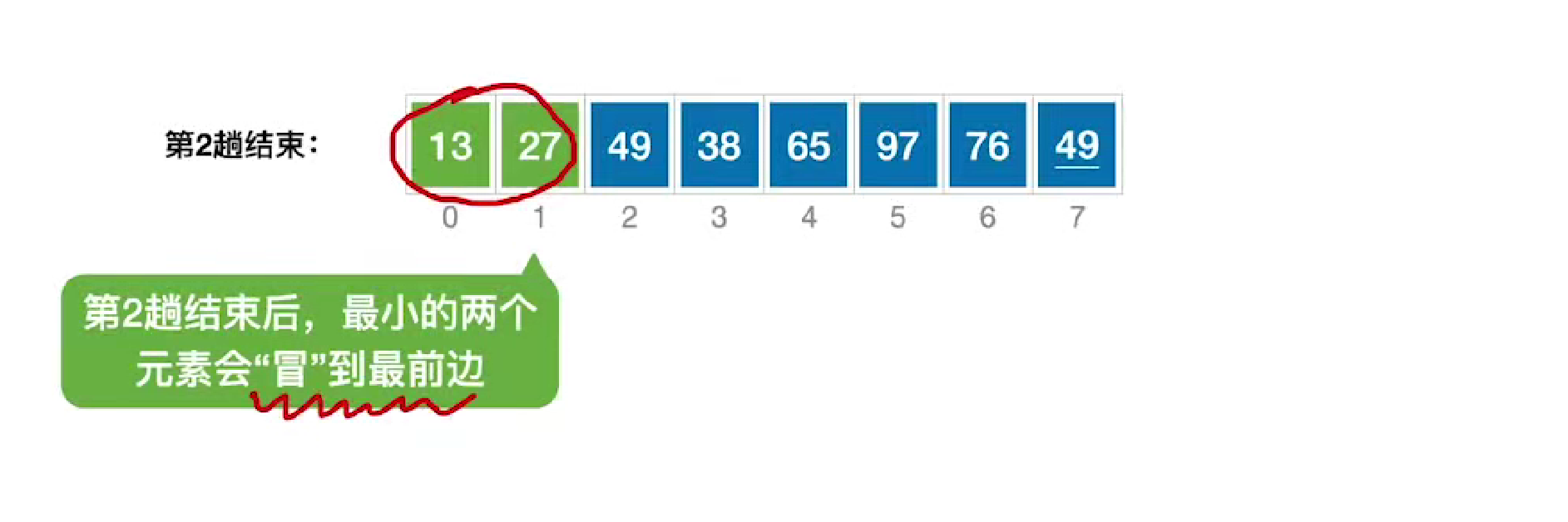

代码实现
flag用于判断是否发生交换,以便于提前跳出循环
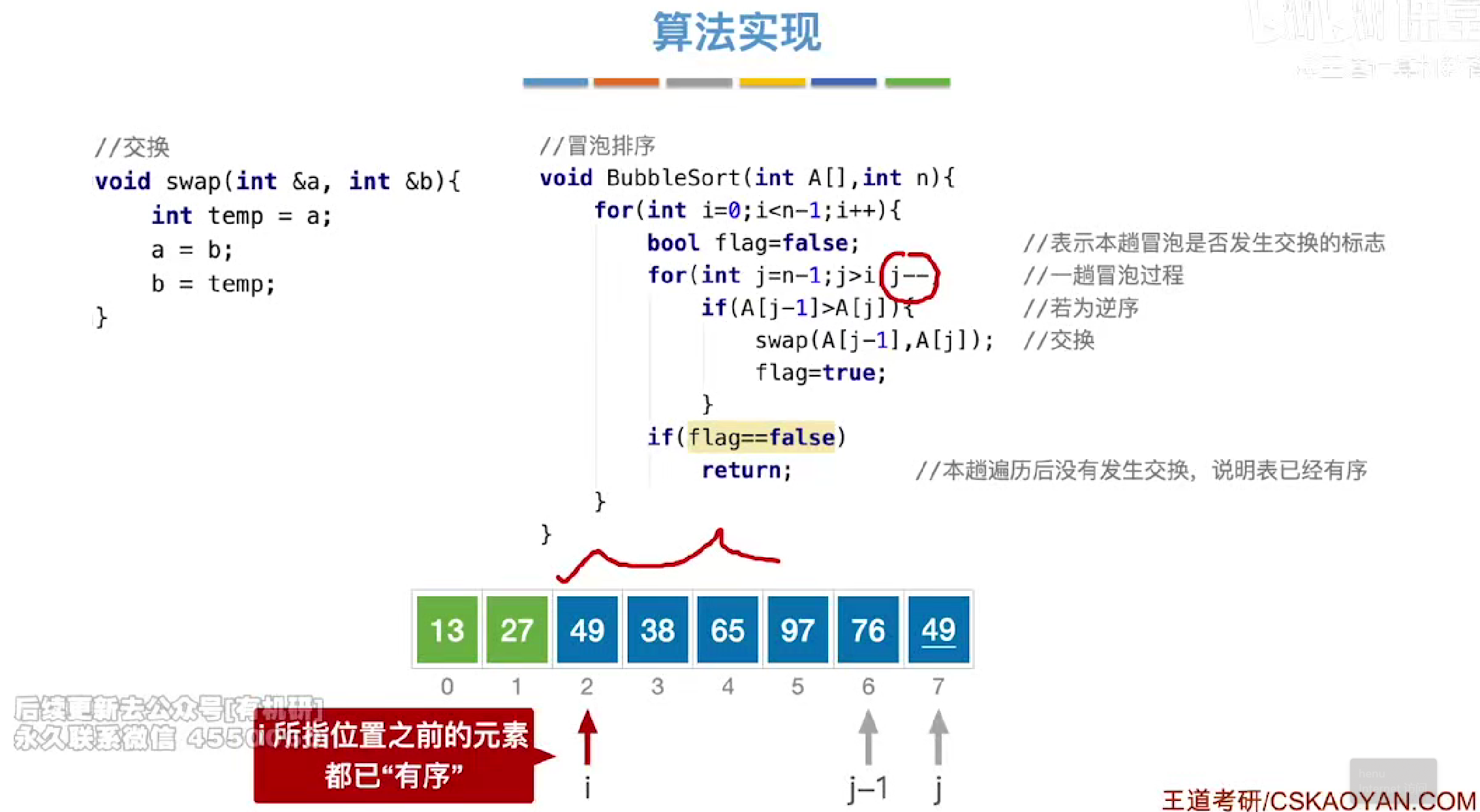
时空复杂度
平均依旧是n²
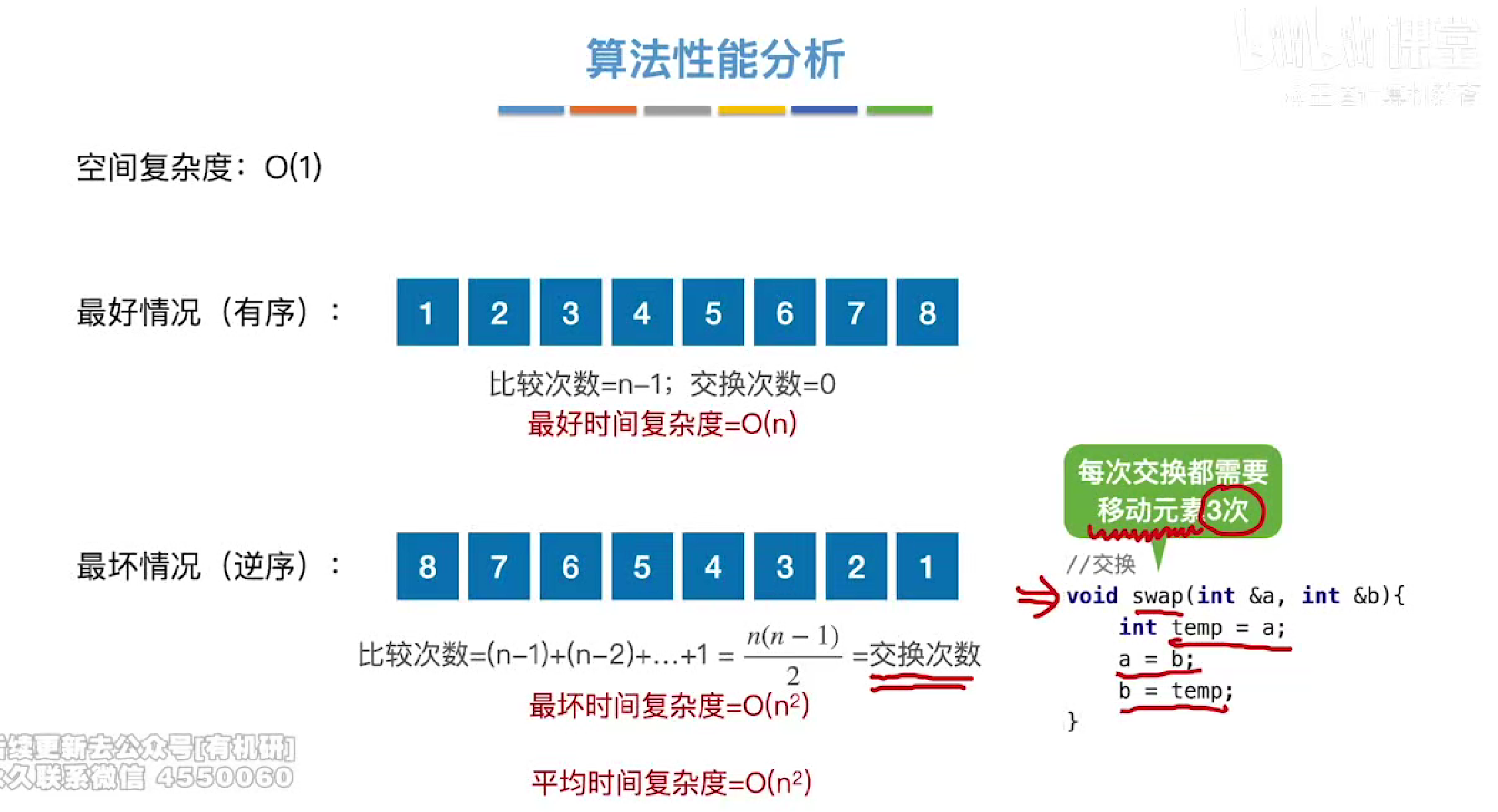
链表实现
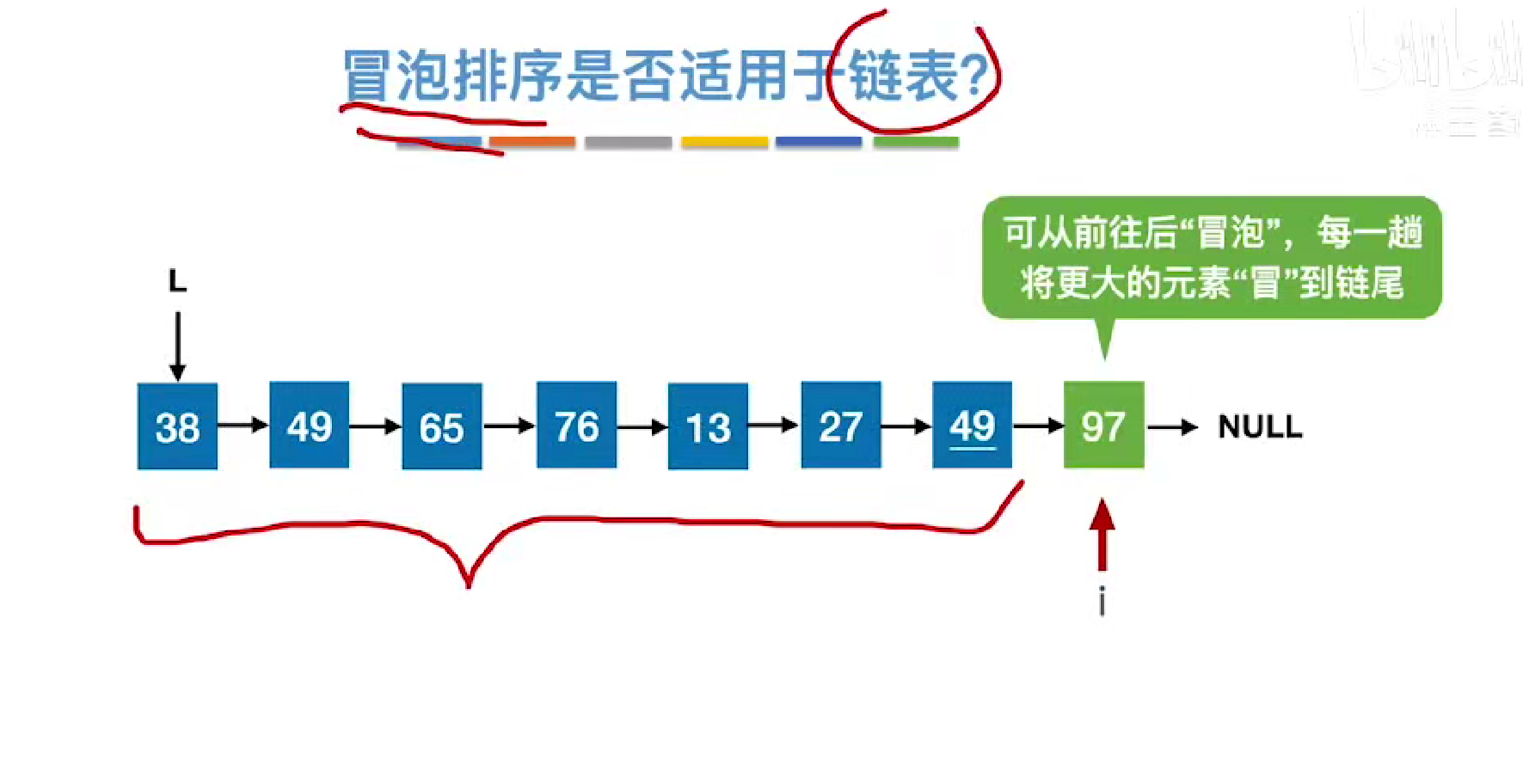
快排(要会写代码)
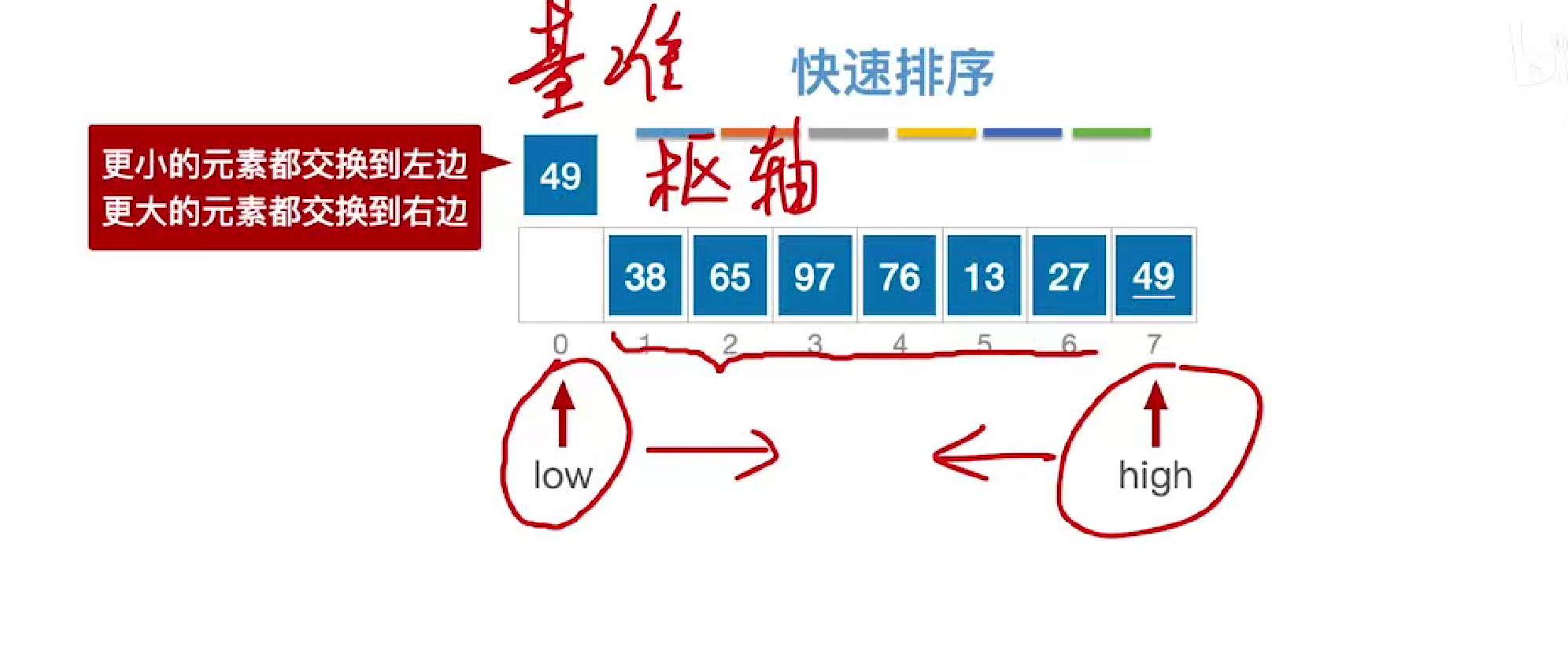
简单来说就是选择数组开头的元素,作为基准进行划分为左右两个部分,左边的都小于basic,右边的都大于basic
然后首位两个指针从0和n-1依次往后判断
首先从后判断,直到遇见第一个小于基准basic的元素
然后和low发生交换
此时low指向的指针一定会小于基准,所以我们判断完一次hight之后选择判断low
此时low指针在一次交换过后直接++
然后接着判断是否小于基准,直到遇见一个大于基准的元素,然后交换
然后再判断hight
直到两个指针相遇,此时将基准放入
即可划分两个子区间
然后我们在递归的对左右两个子表进行划分
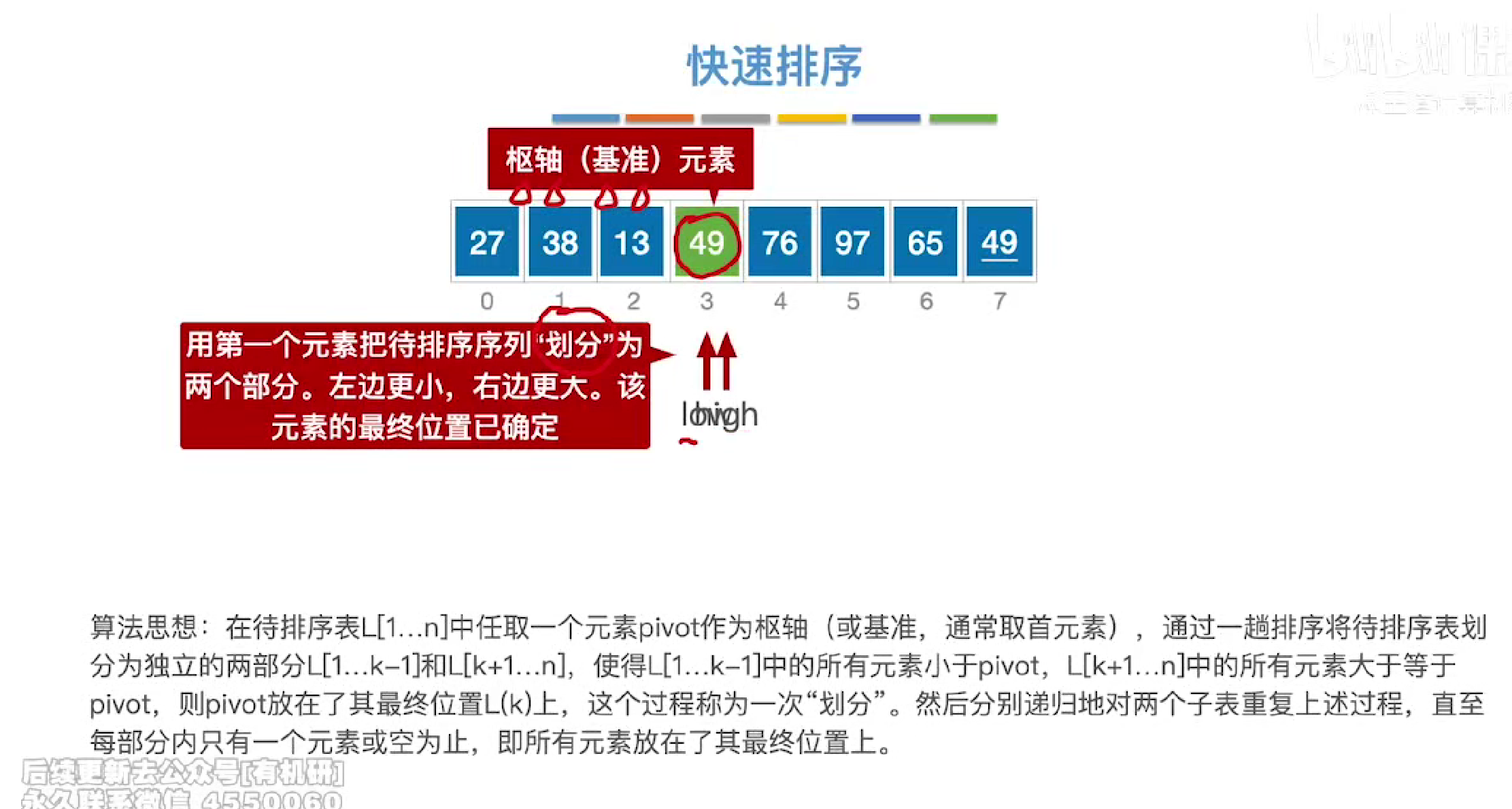
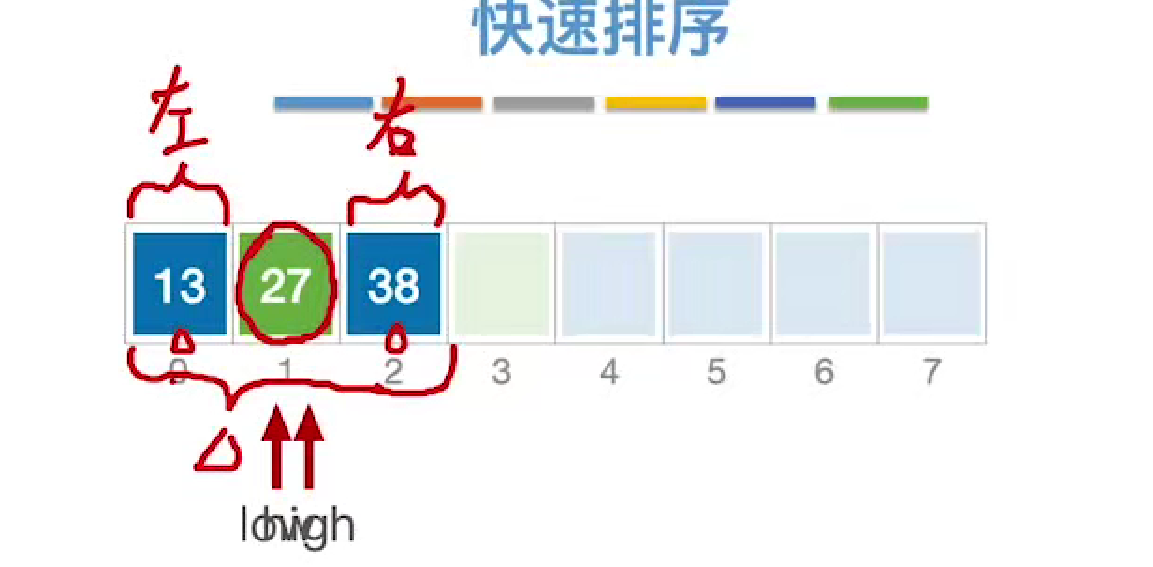
当再次递归后,如果左右两个子区间元素长度都为1,则直接return终止运行
代码实现

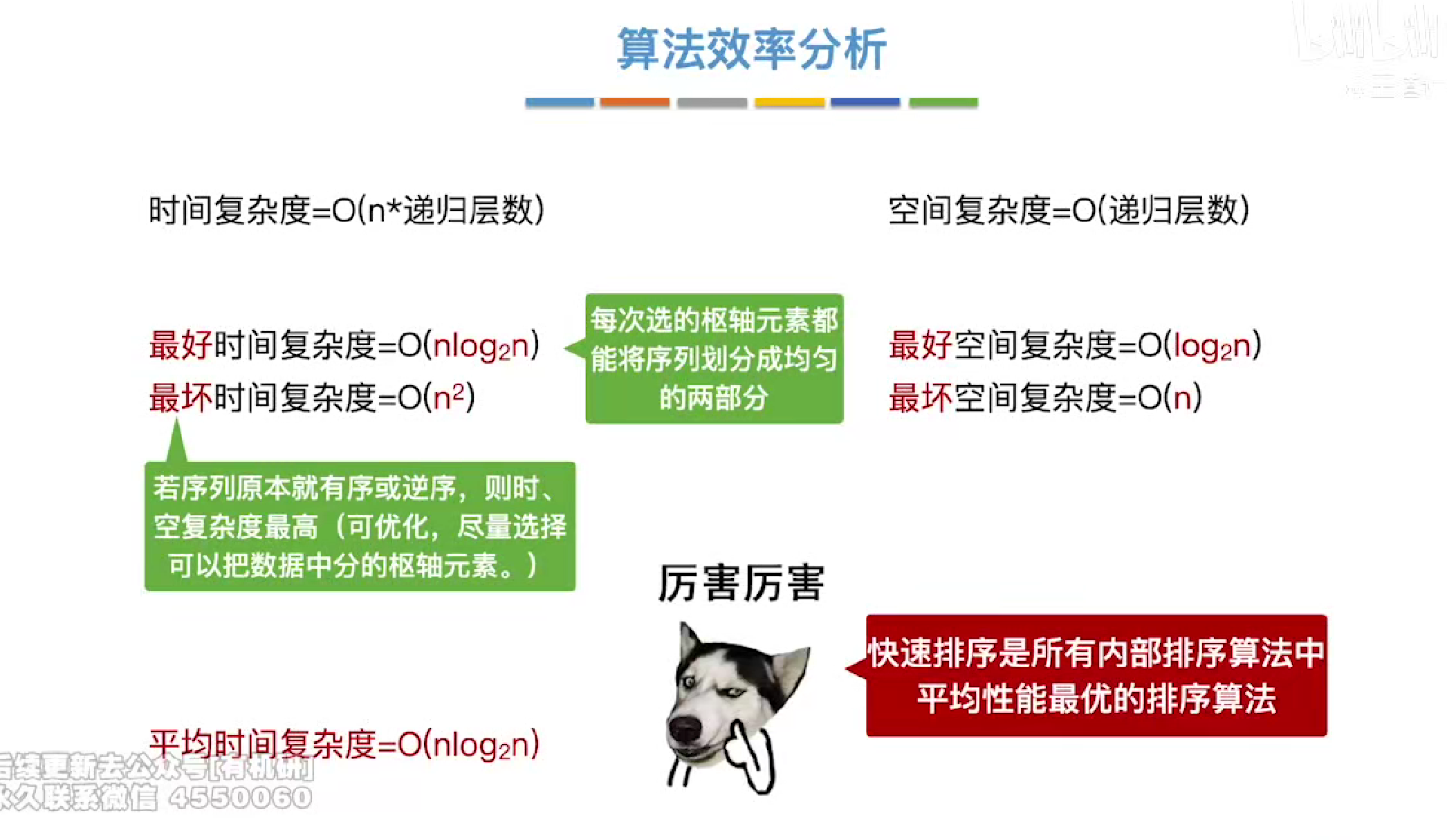
时空复杂度
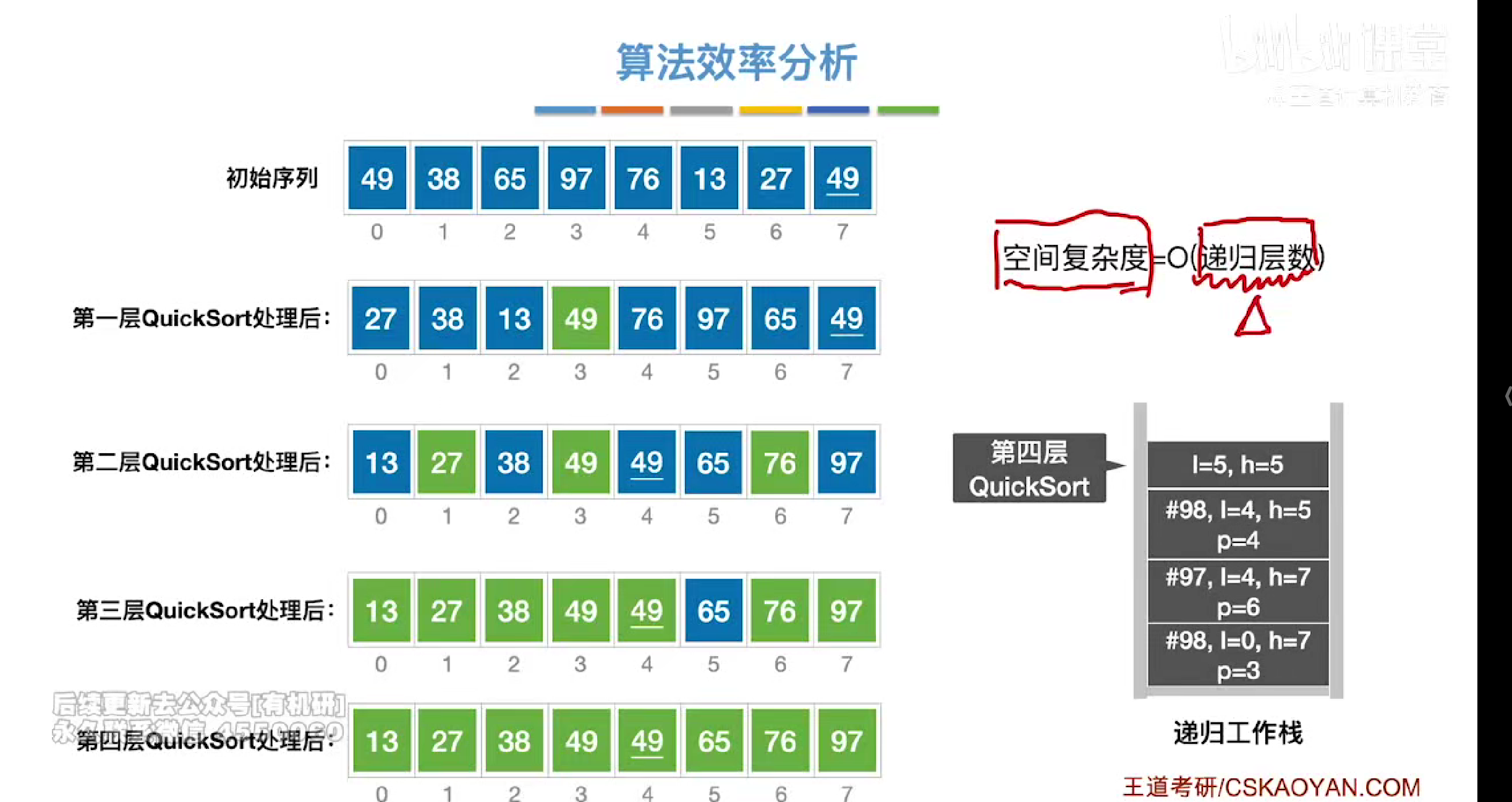
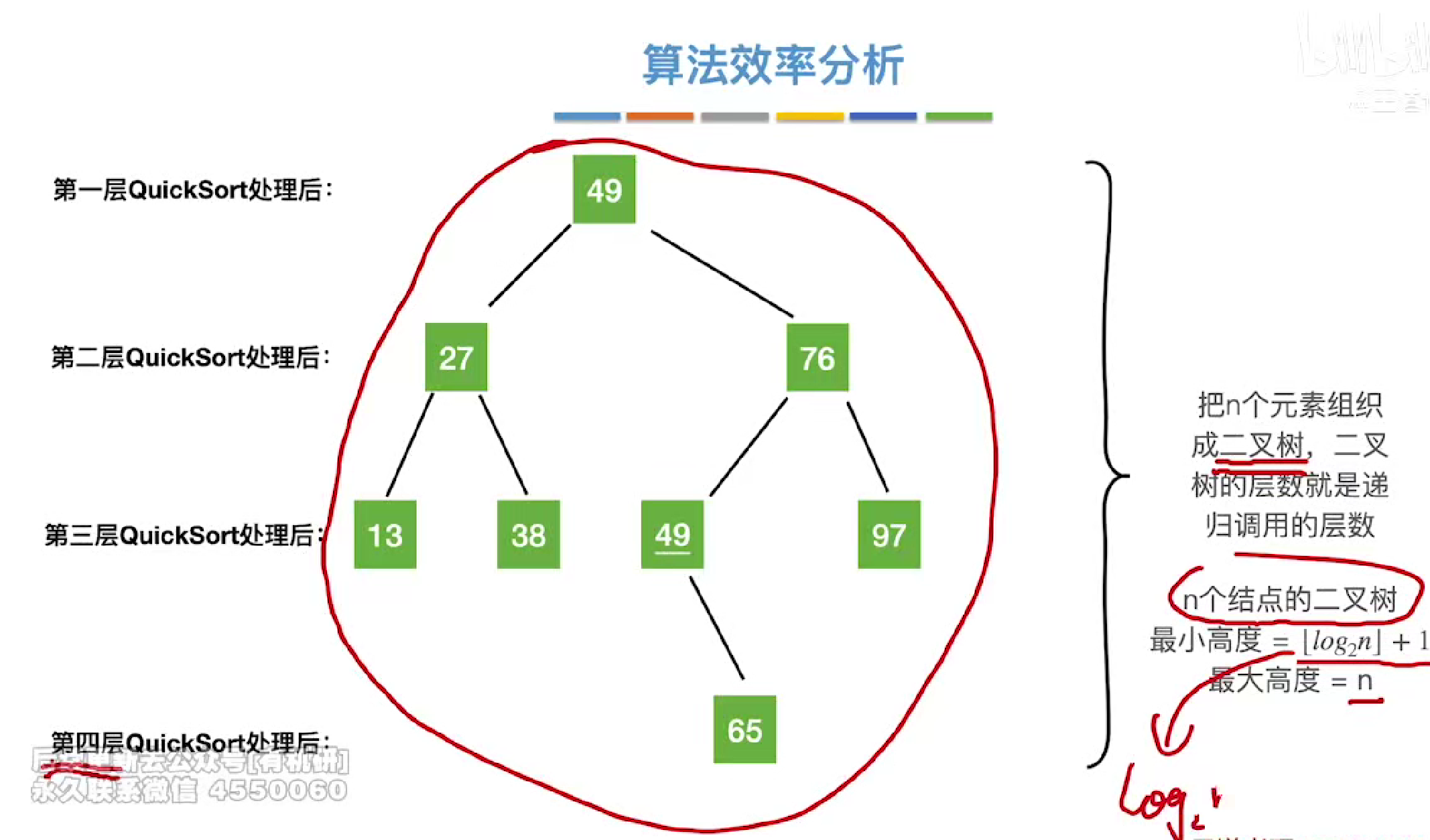
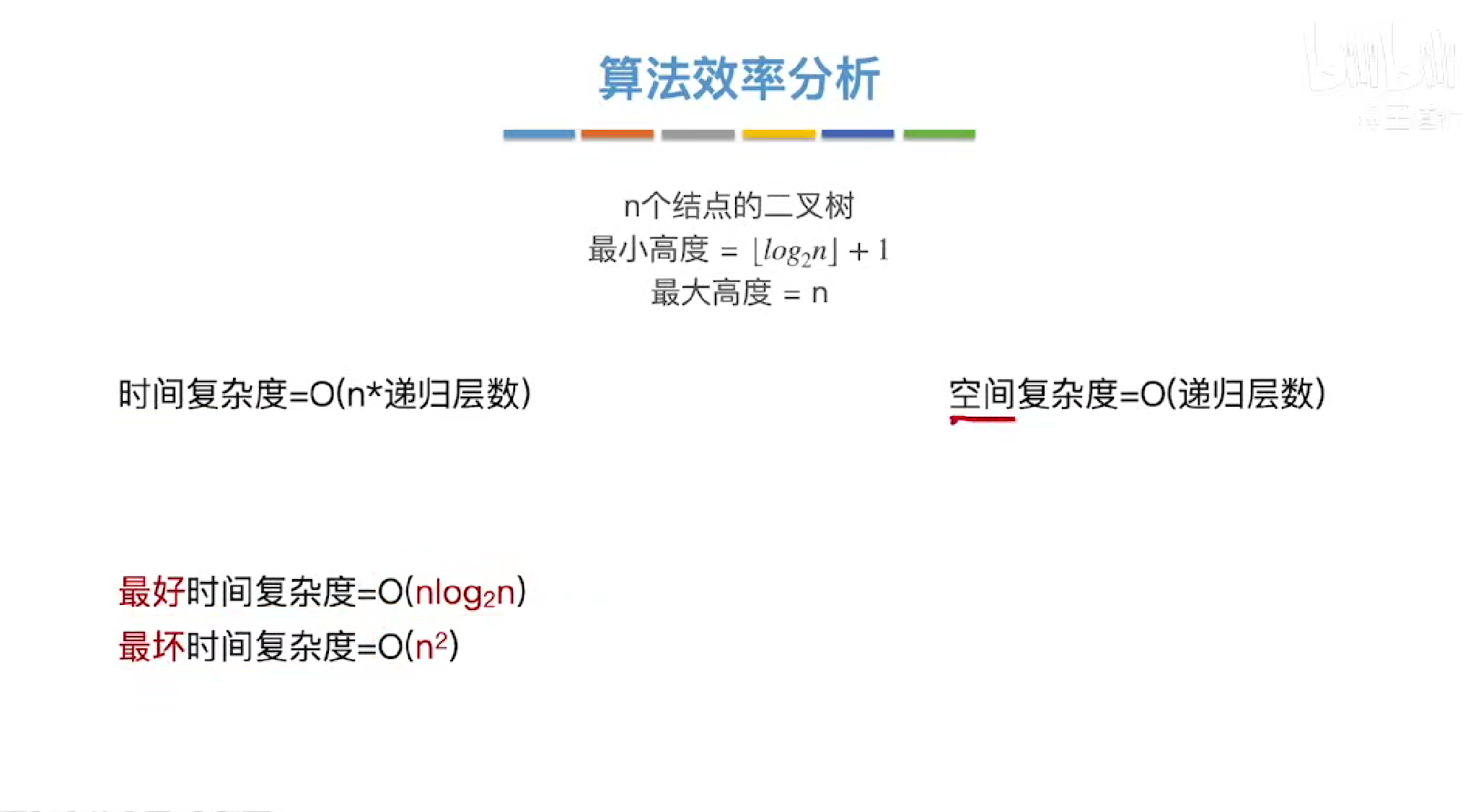
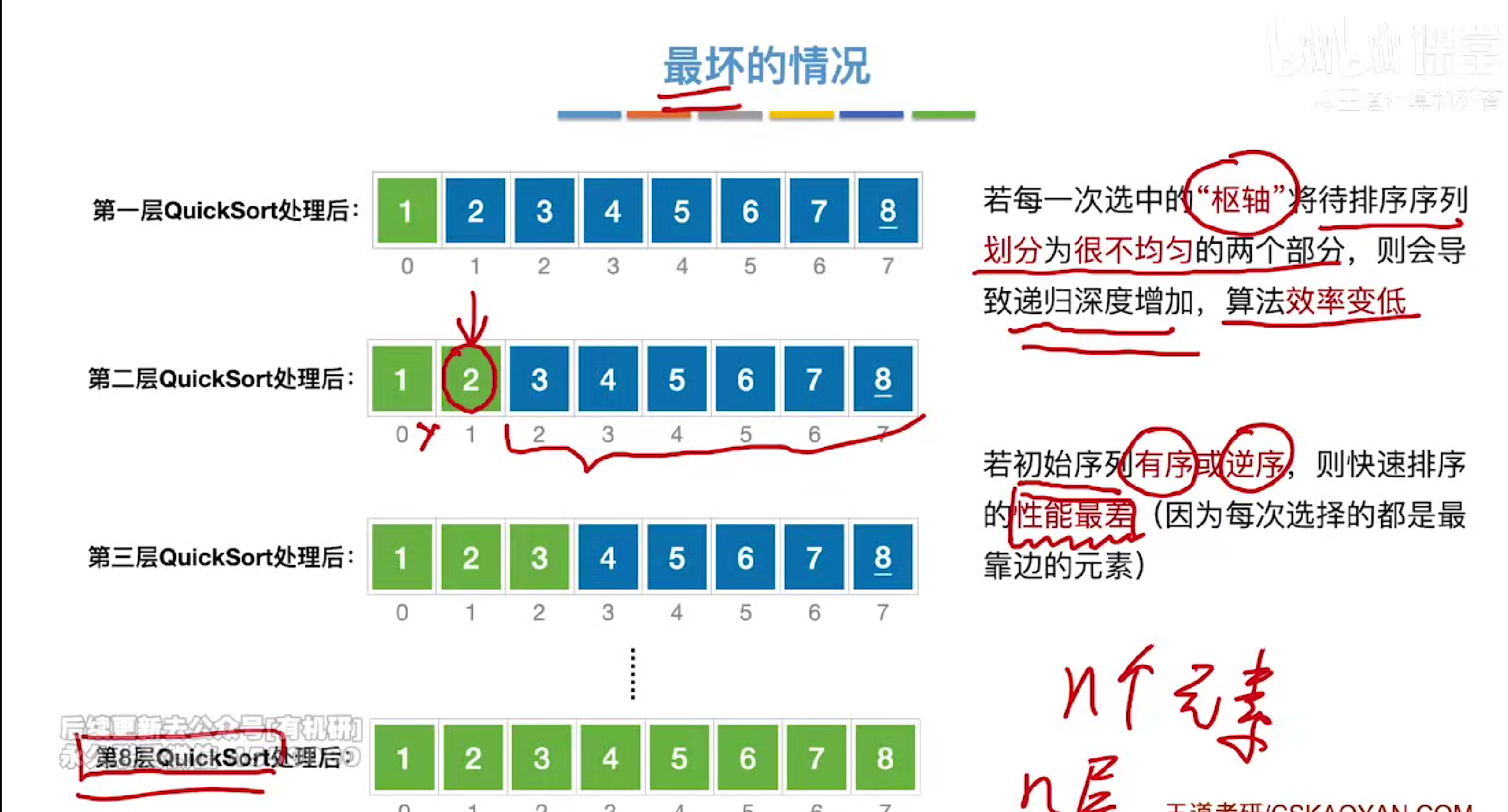
优化


简单选择排序
每次选择一个最小的与开头互换
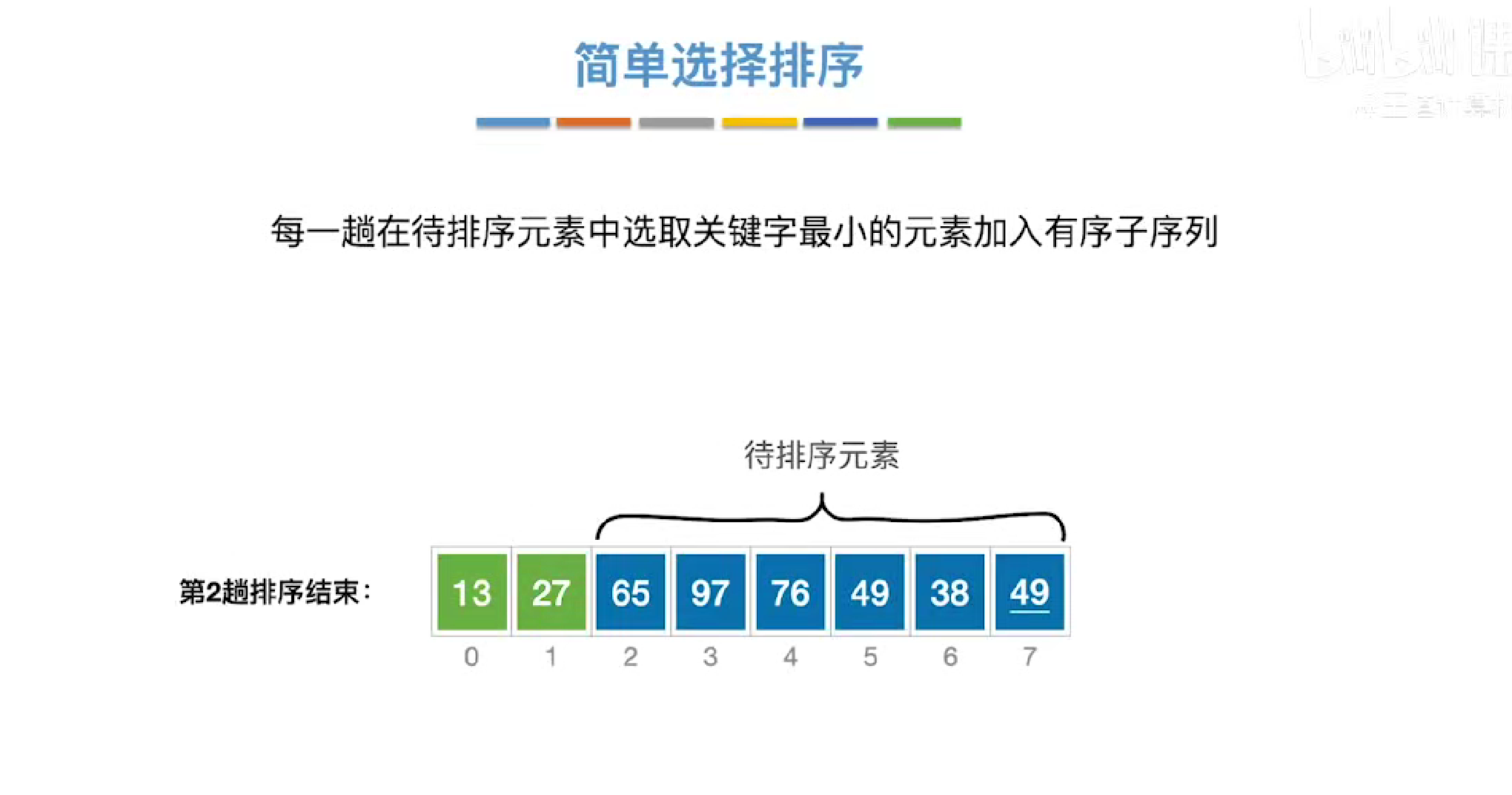


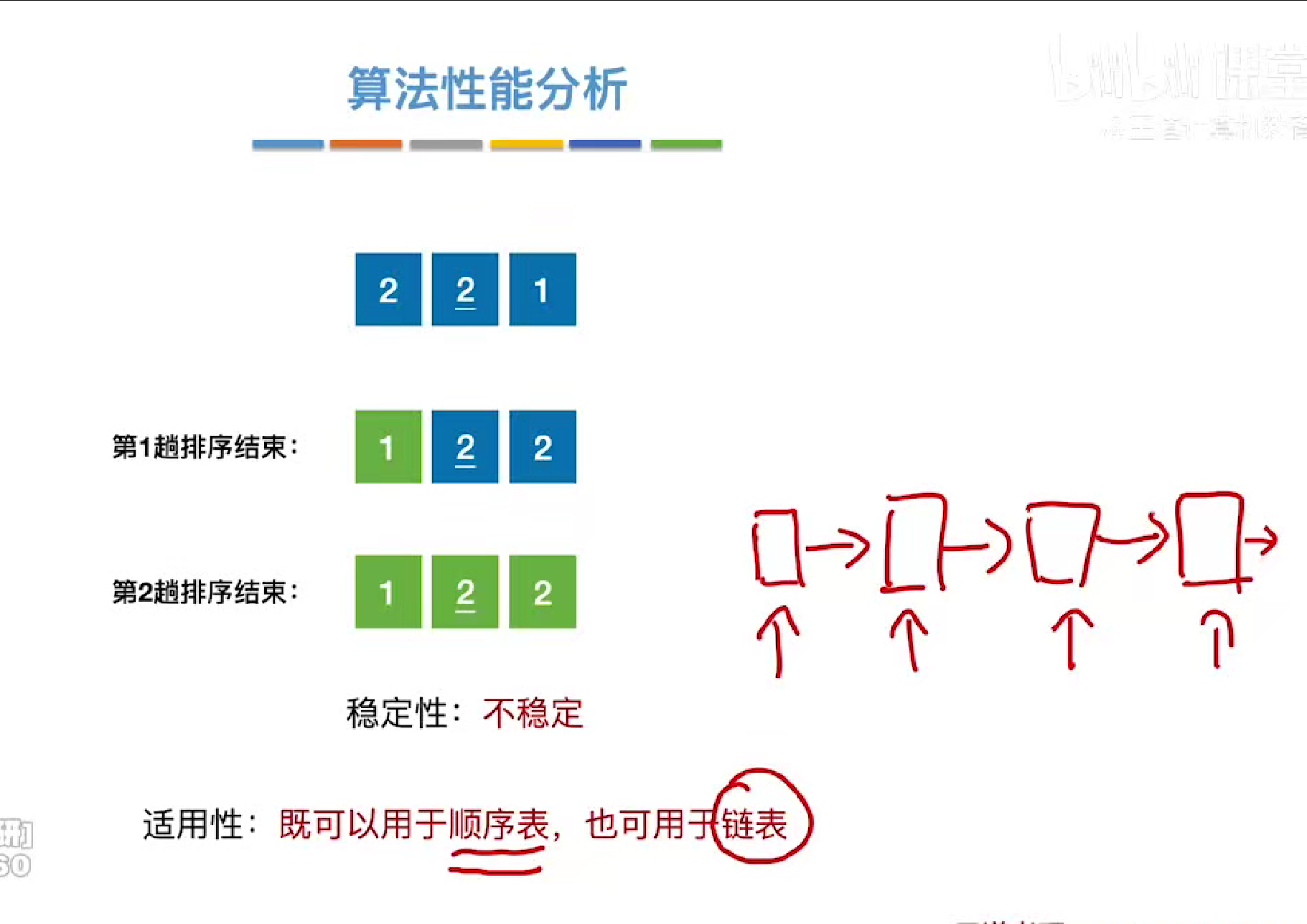
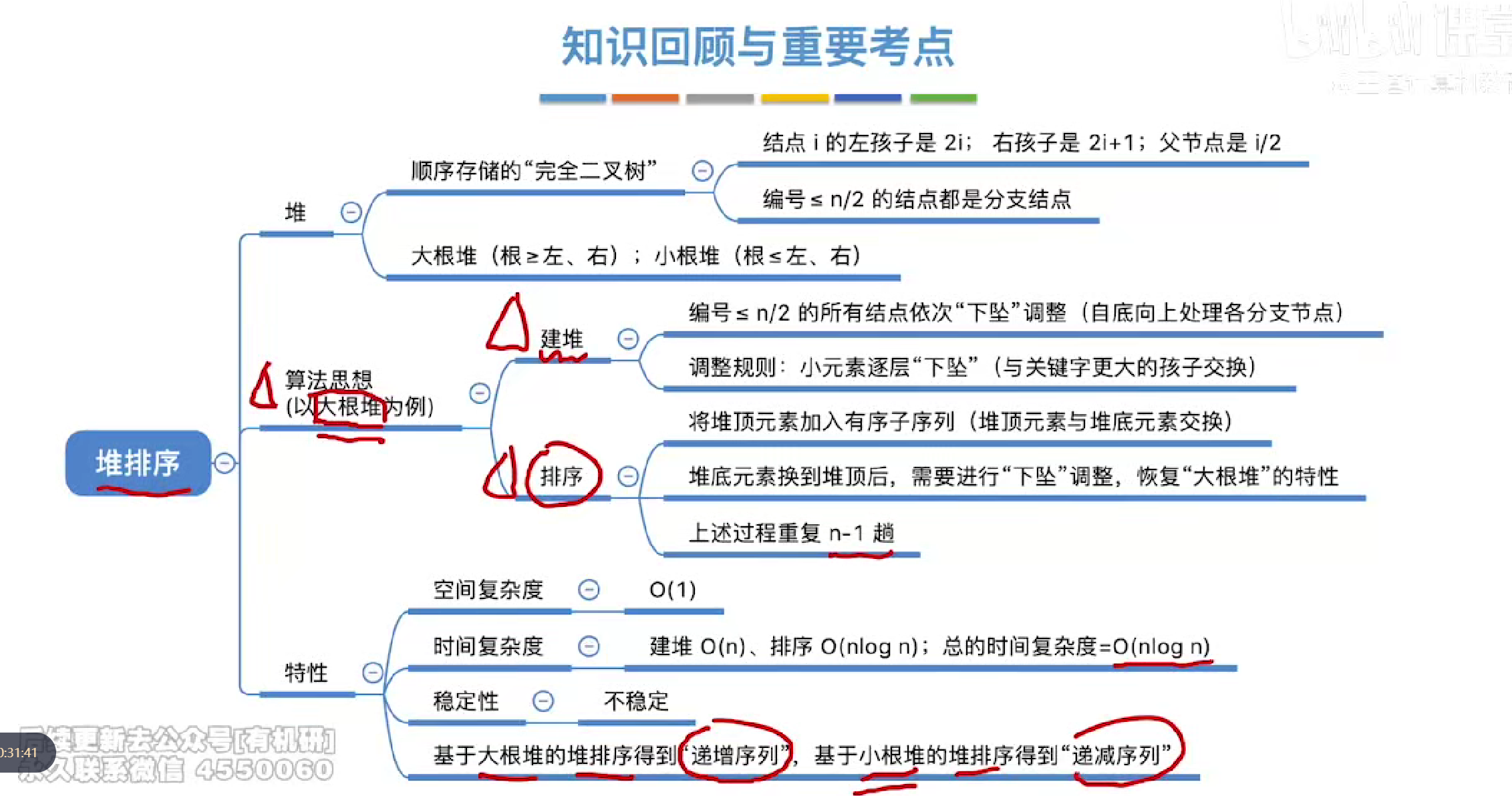
堆排序
定义
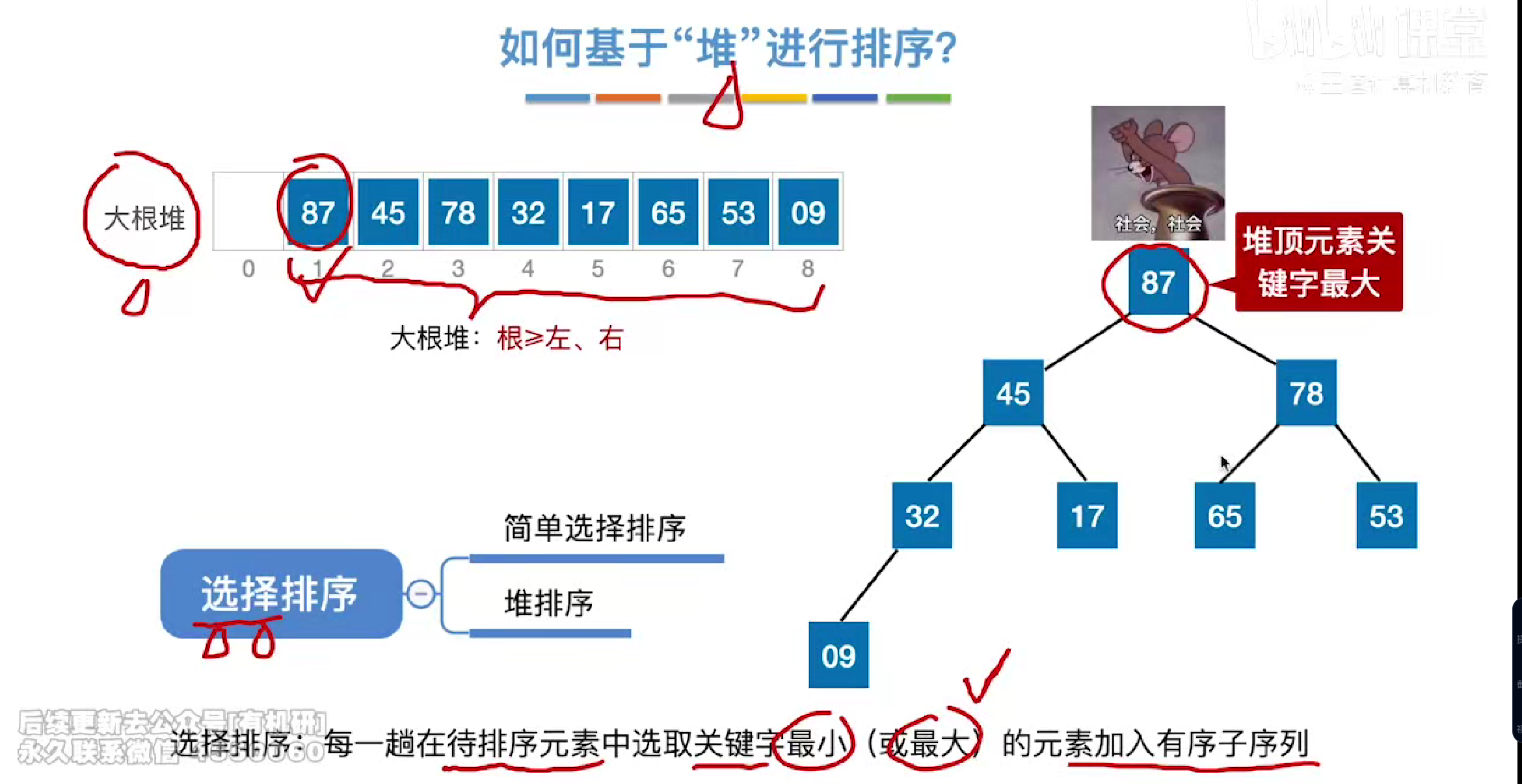
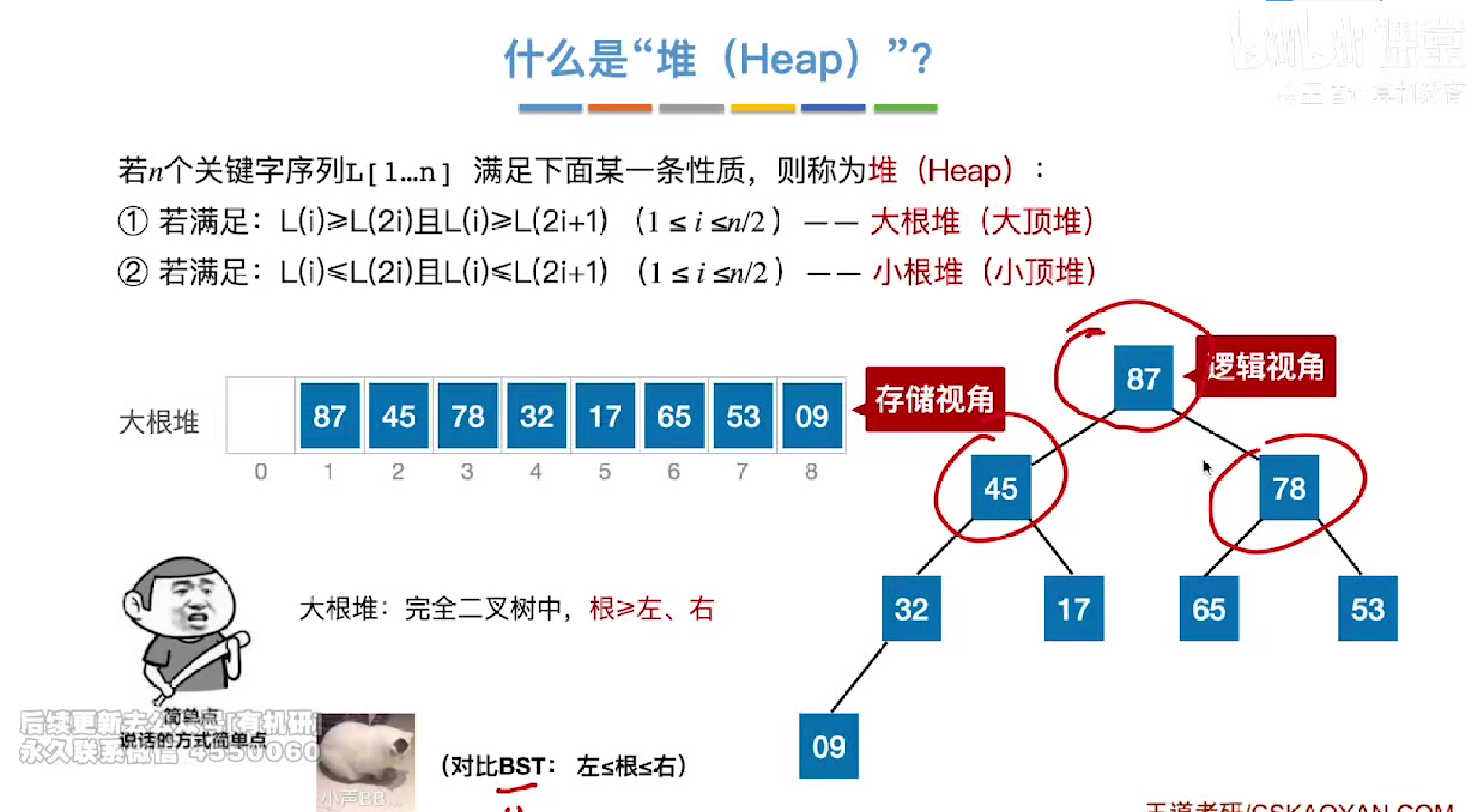
大根堆
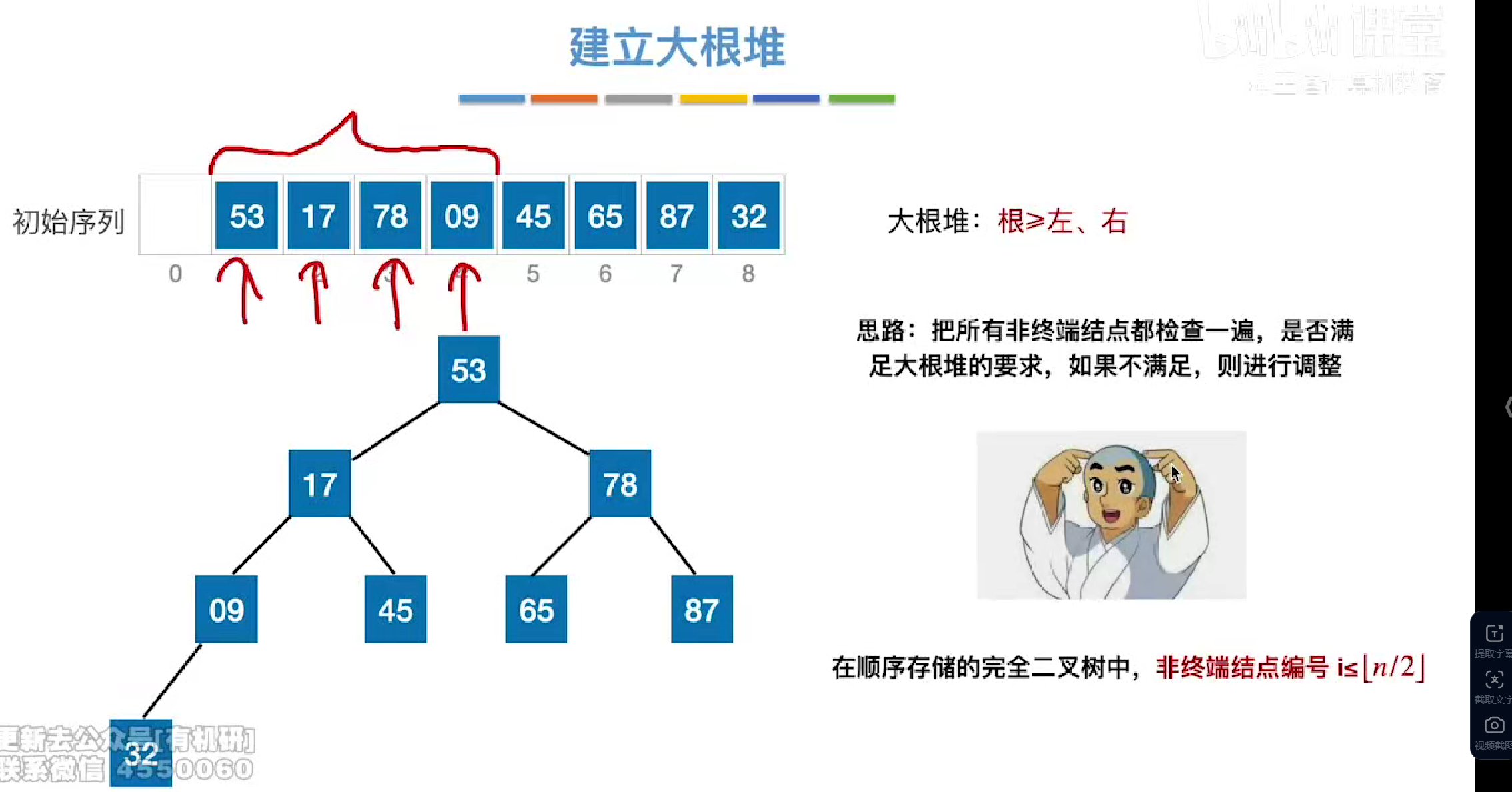
先检查所有分支节点观察是否符合,分支节点位于i<=[n/2]数组前
根>=左,右
即查找所有孩子中比分支节点更大的结点放入
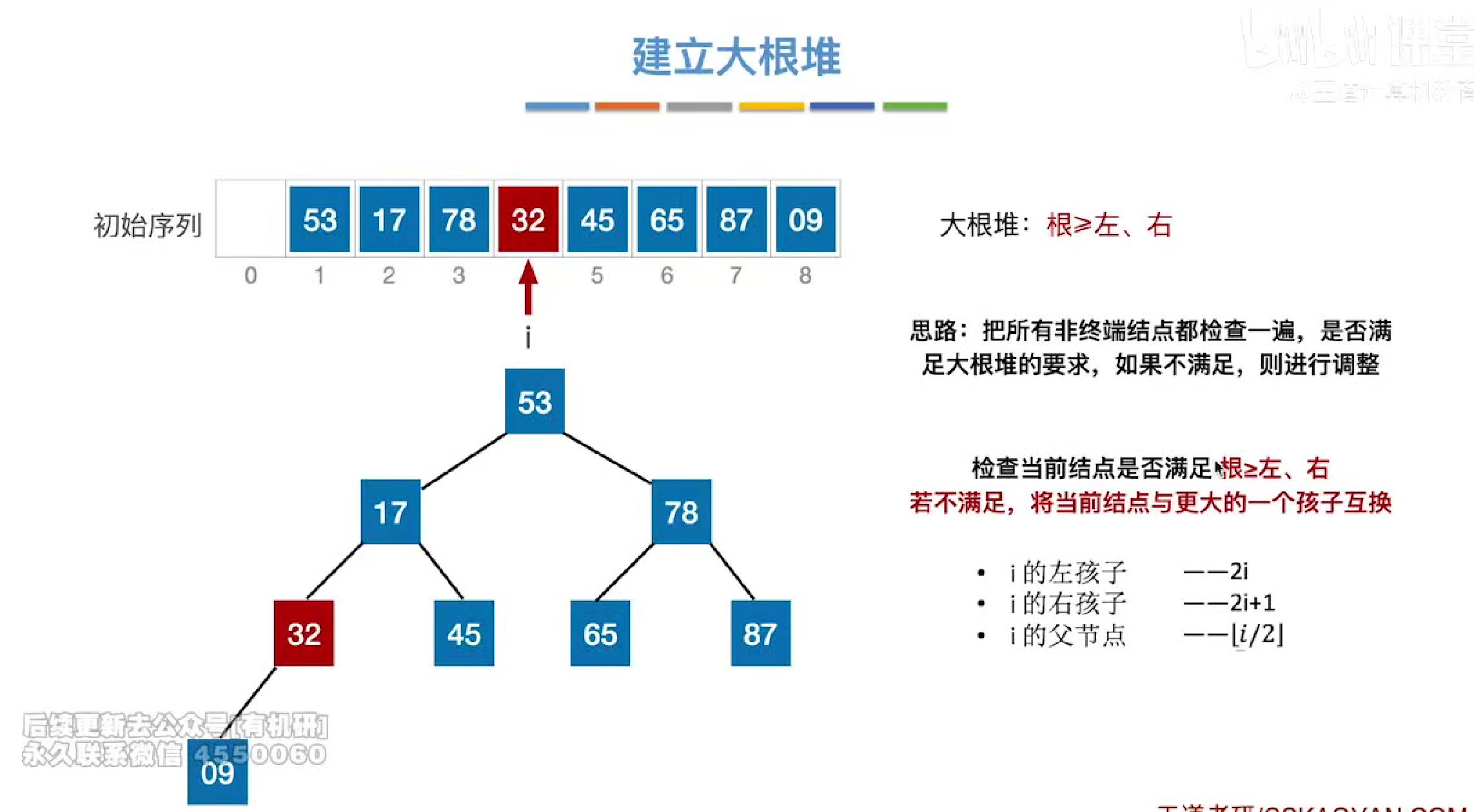
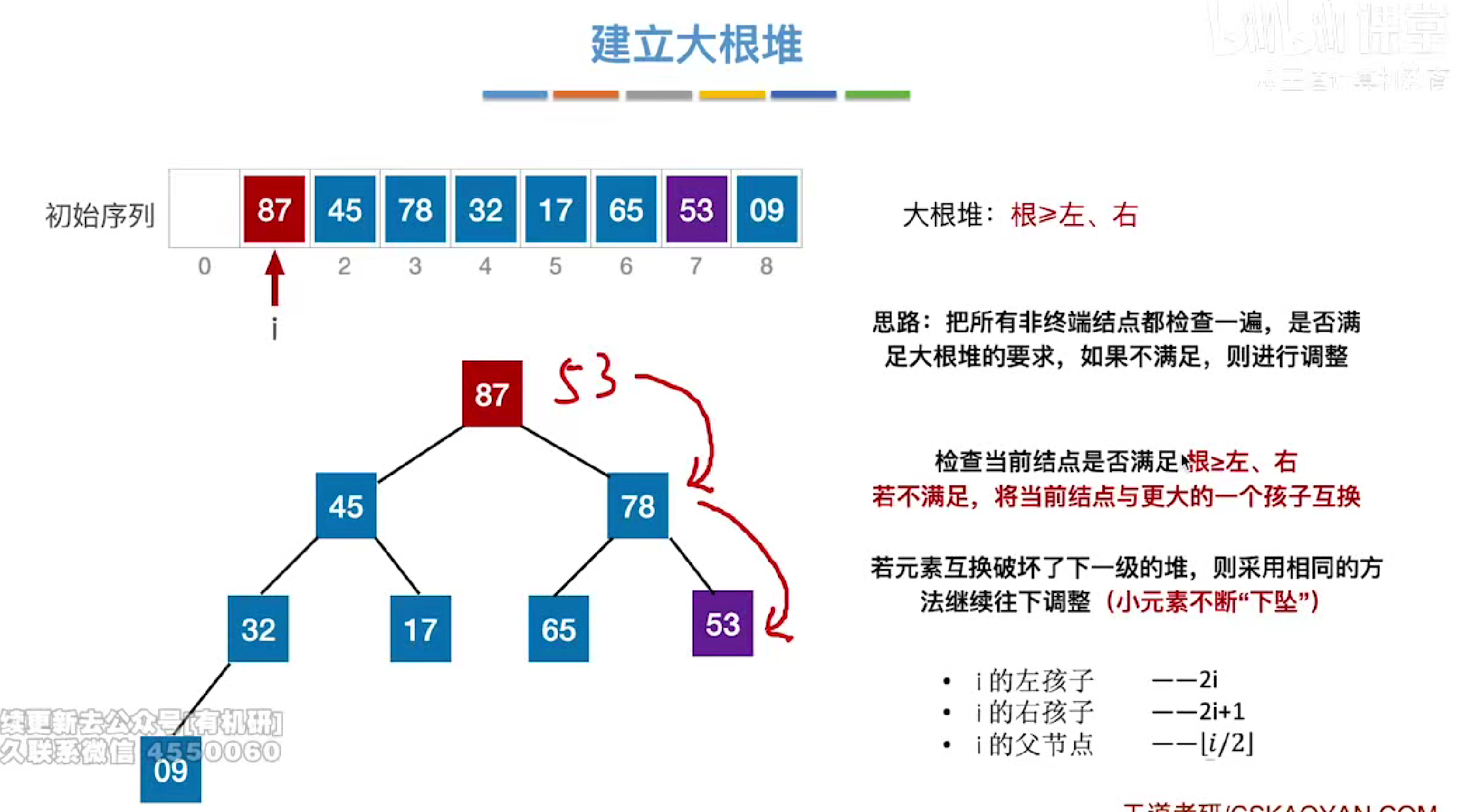
若在互换时连续违反大根堆的定义
则会连续互换
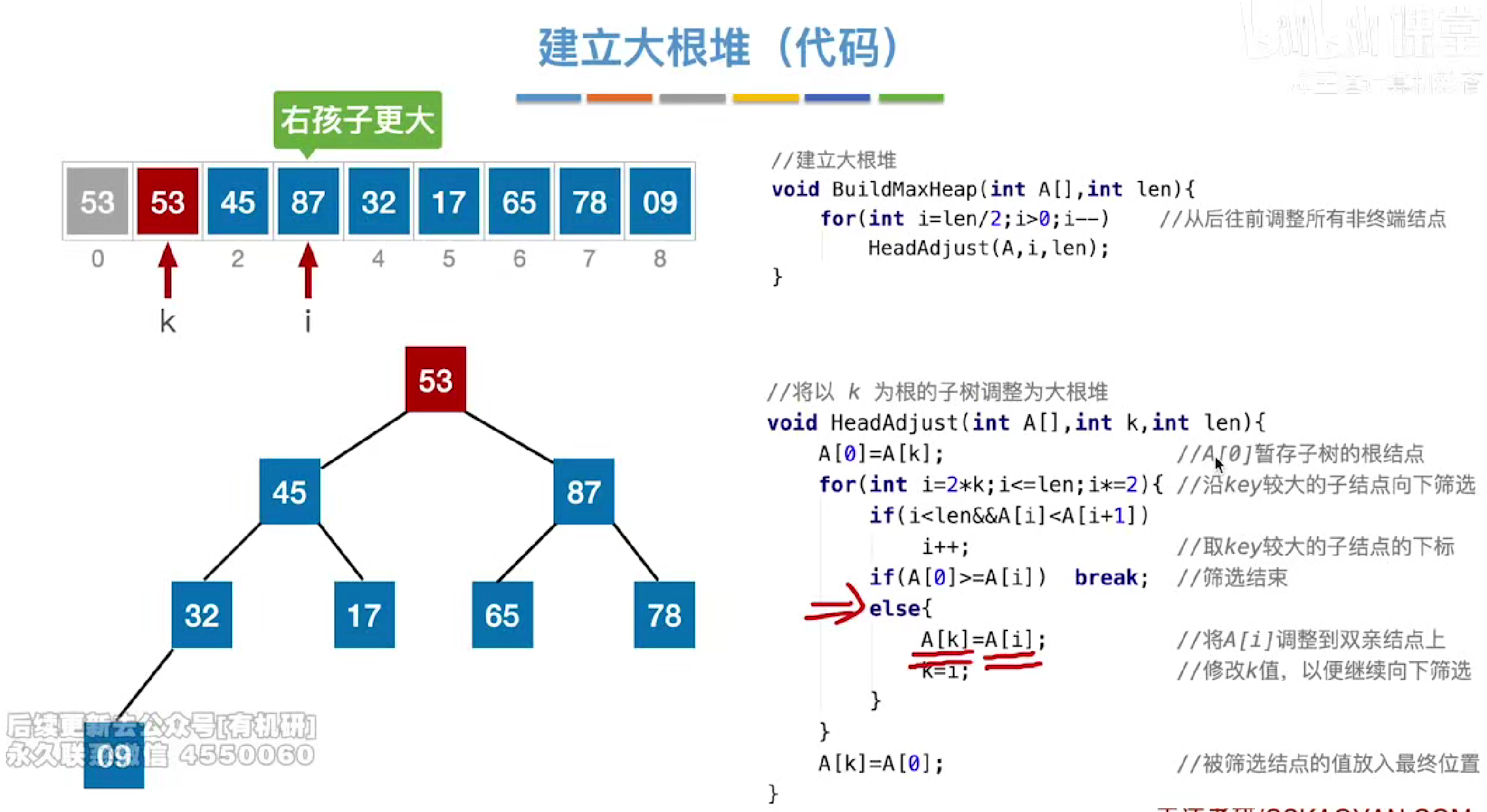
大根堆构建代码实现
for循环的意义是判断完一个结点并完成对应的交换操作的时候,再次观察其子节点是否还有能够互换的结点,其中A[0]就是存储的原本节点的数据,每次都原本根节点数据进行比较,然后每一次互换都会下沉,如果根节点大于其子节点那么就会跳出
第一个if的意义是判断左右孩子哪一个更大,然后再进行与父节点的比较。
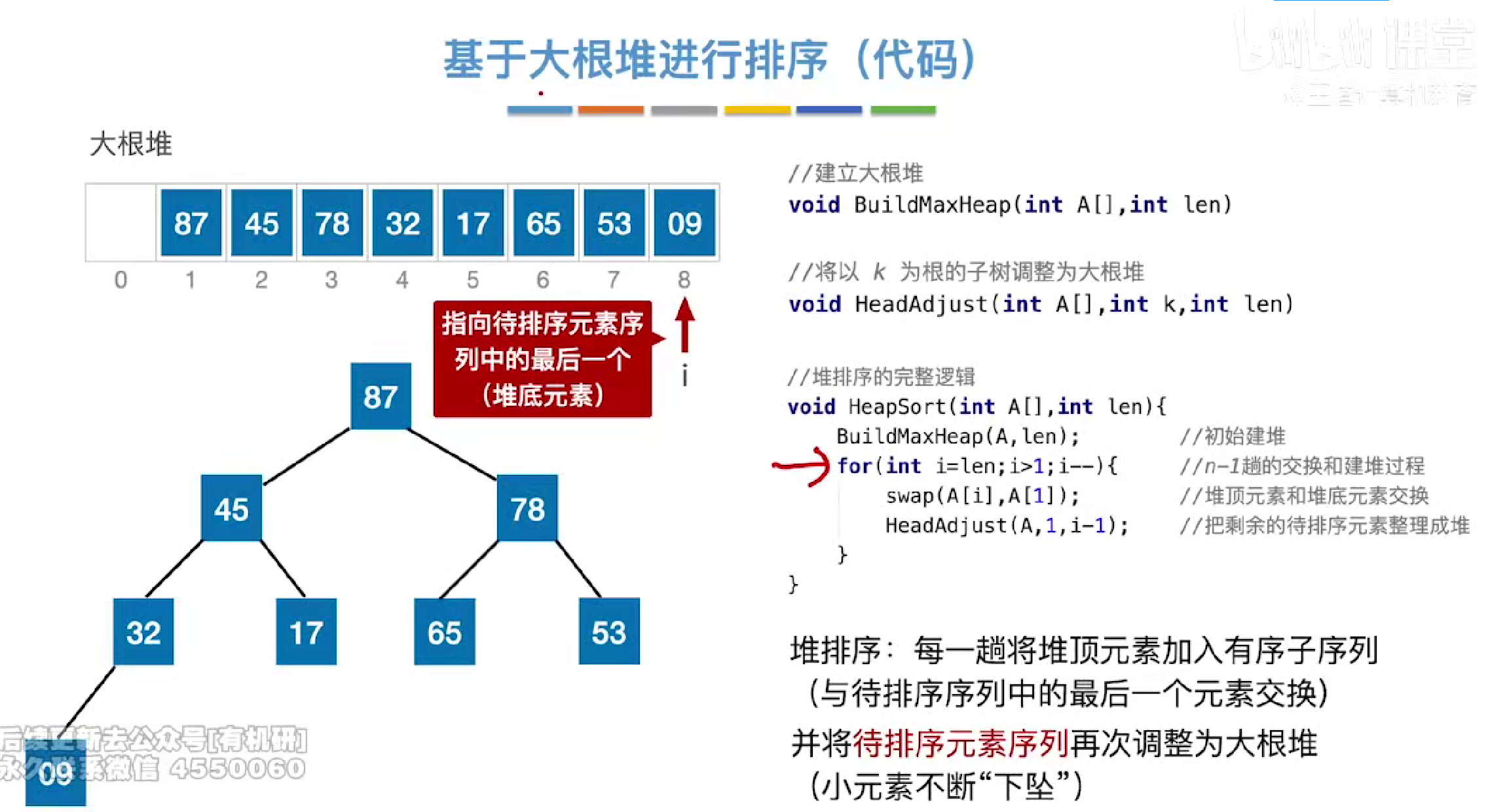
大根堆实现排序
实例
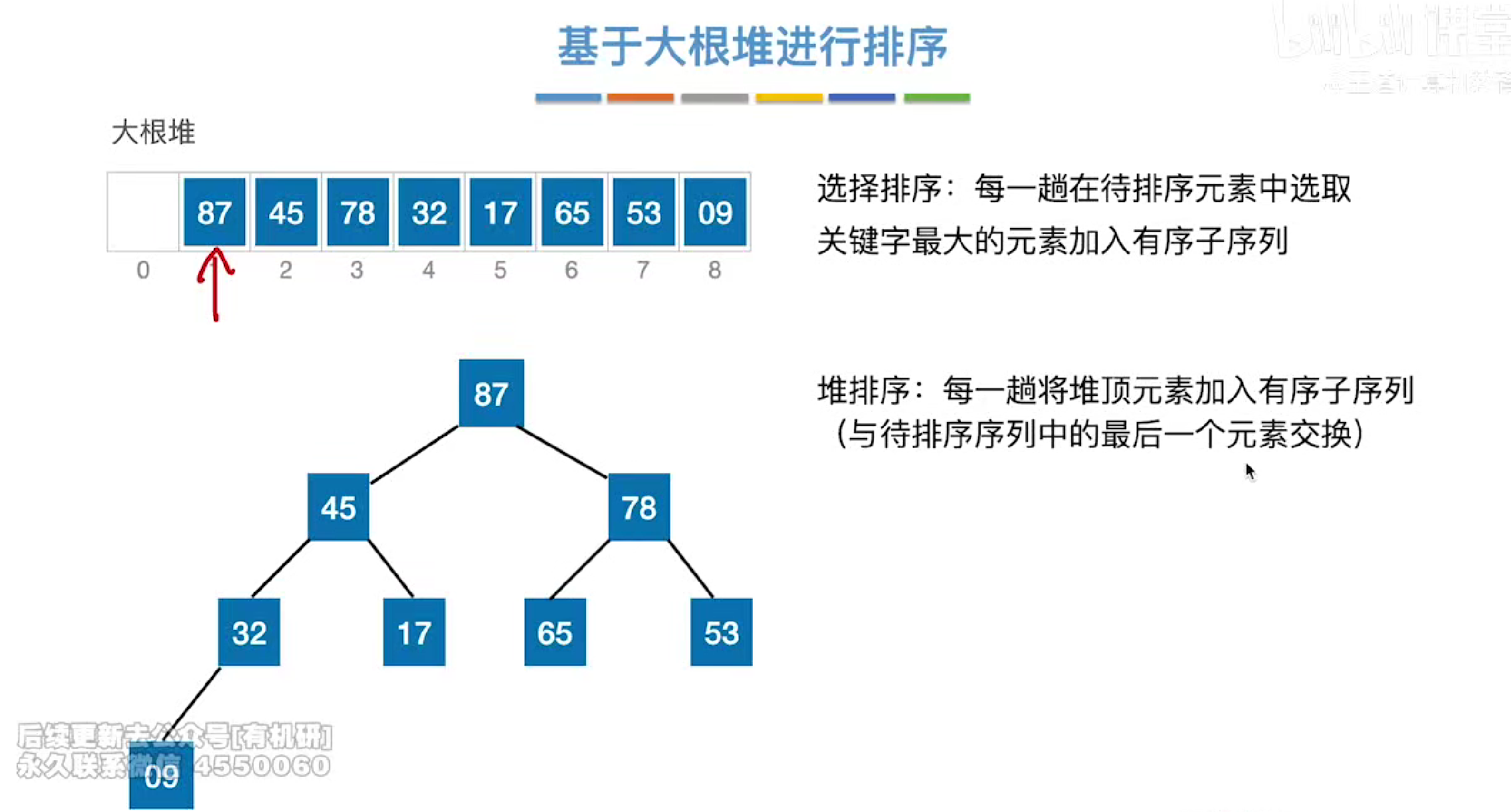
第一趟把87和9交换
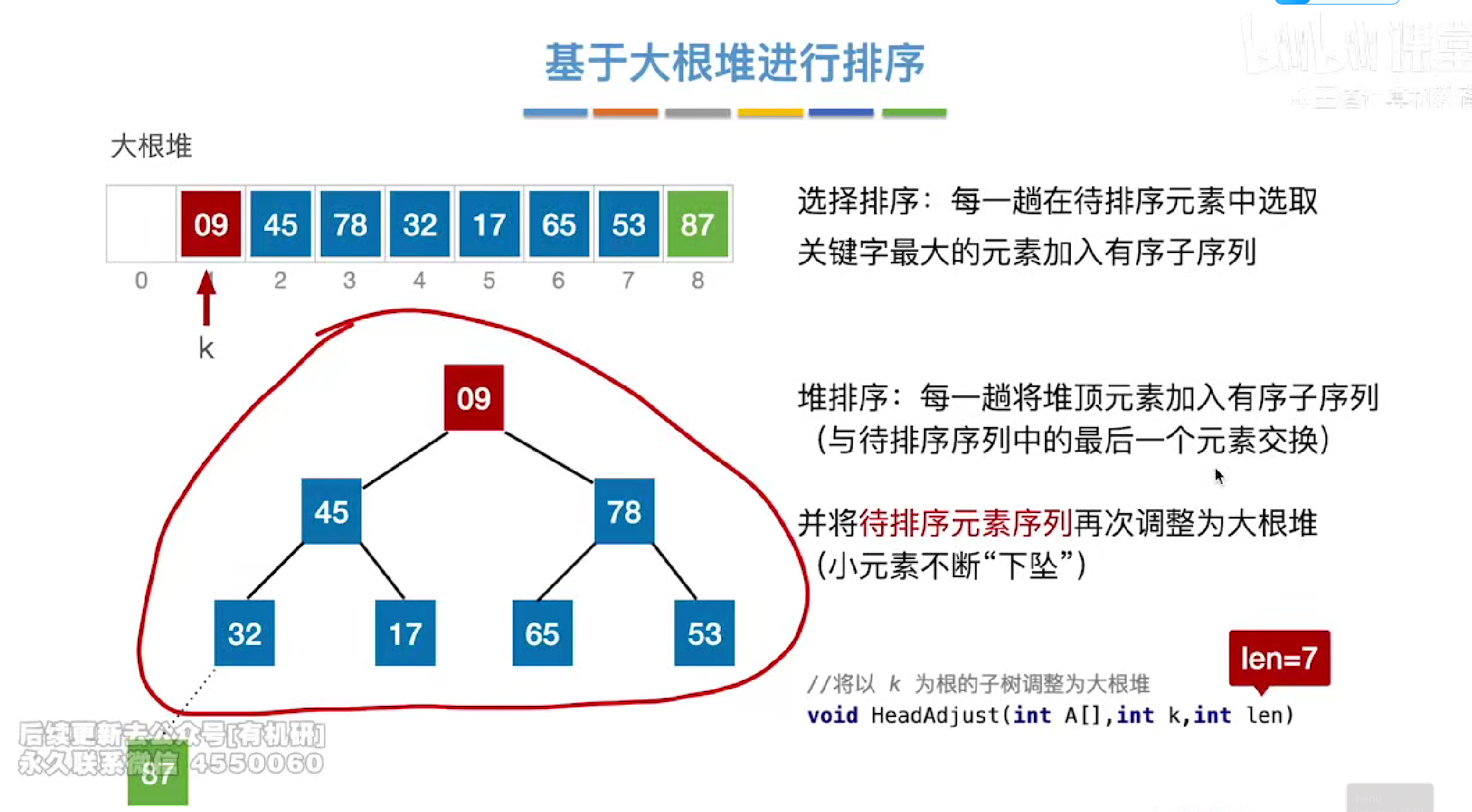
下坠完毕
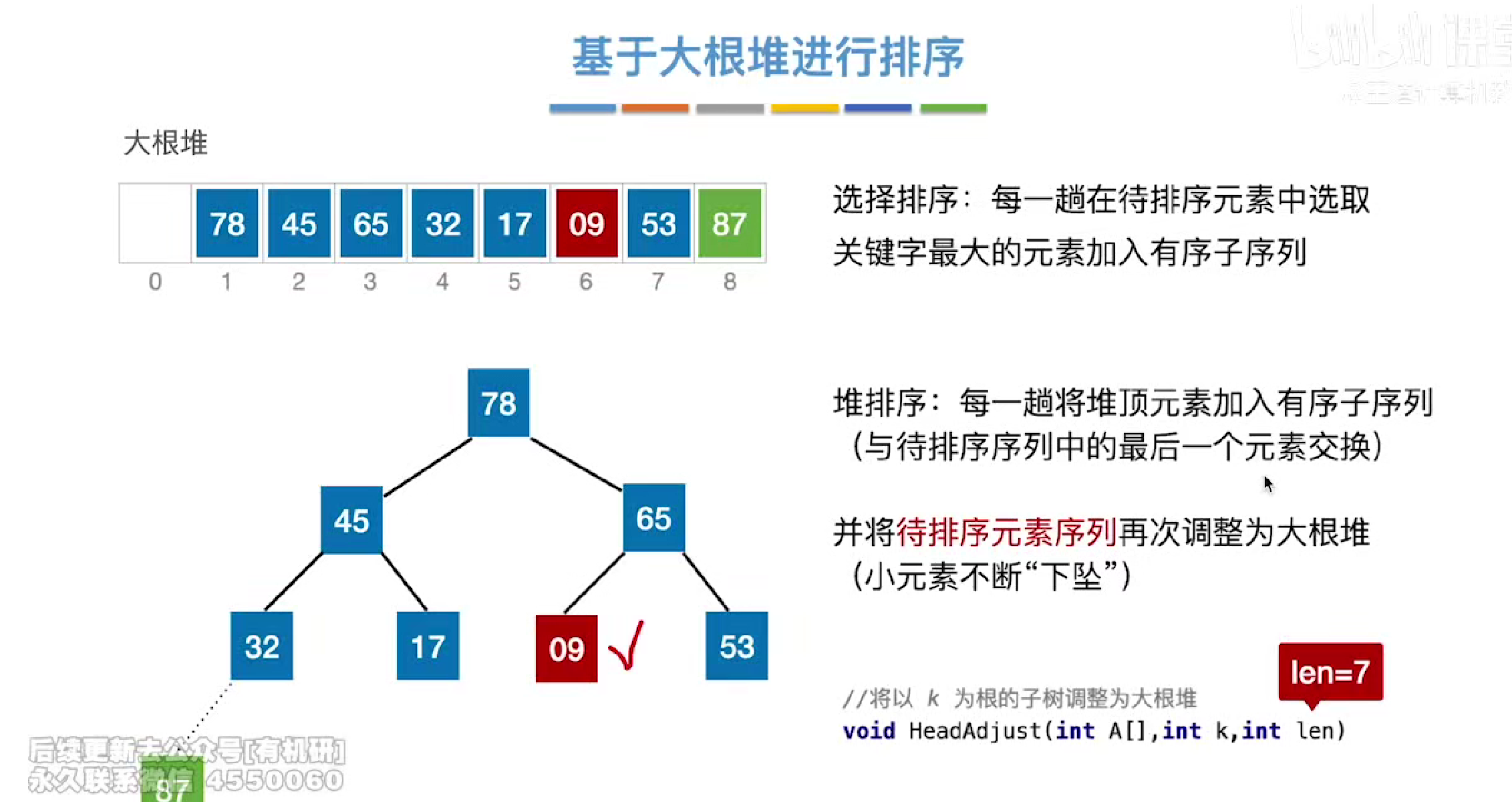
第二次又选择78与末尾进行交换
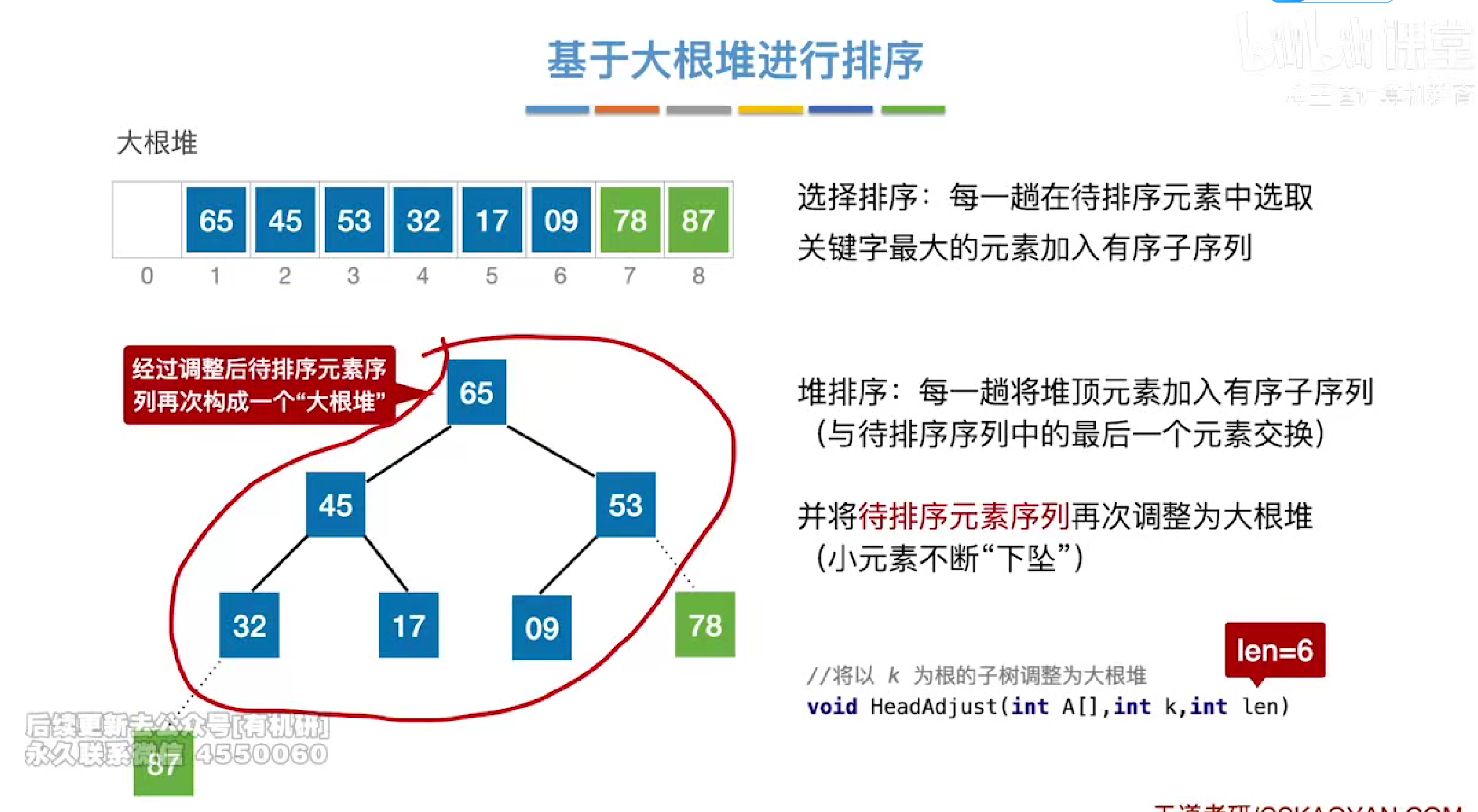

代码实现
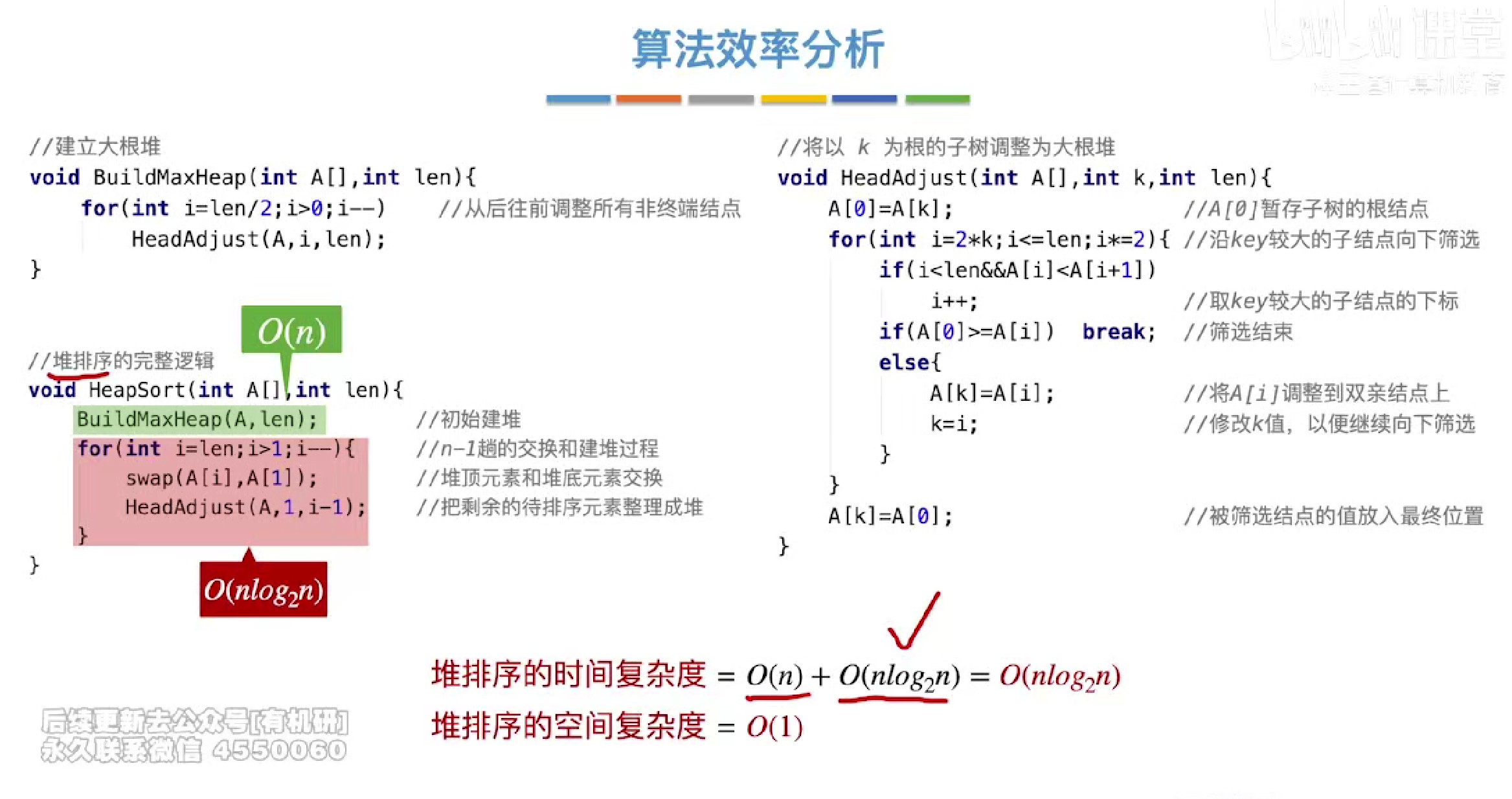
时空复杂度



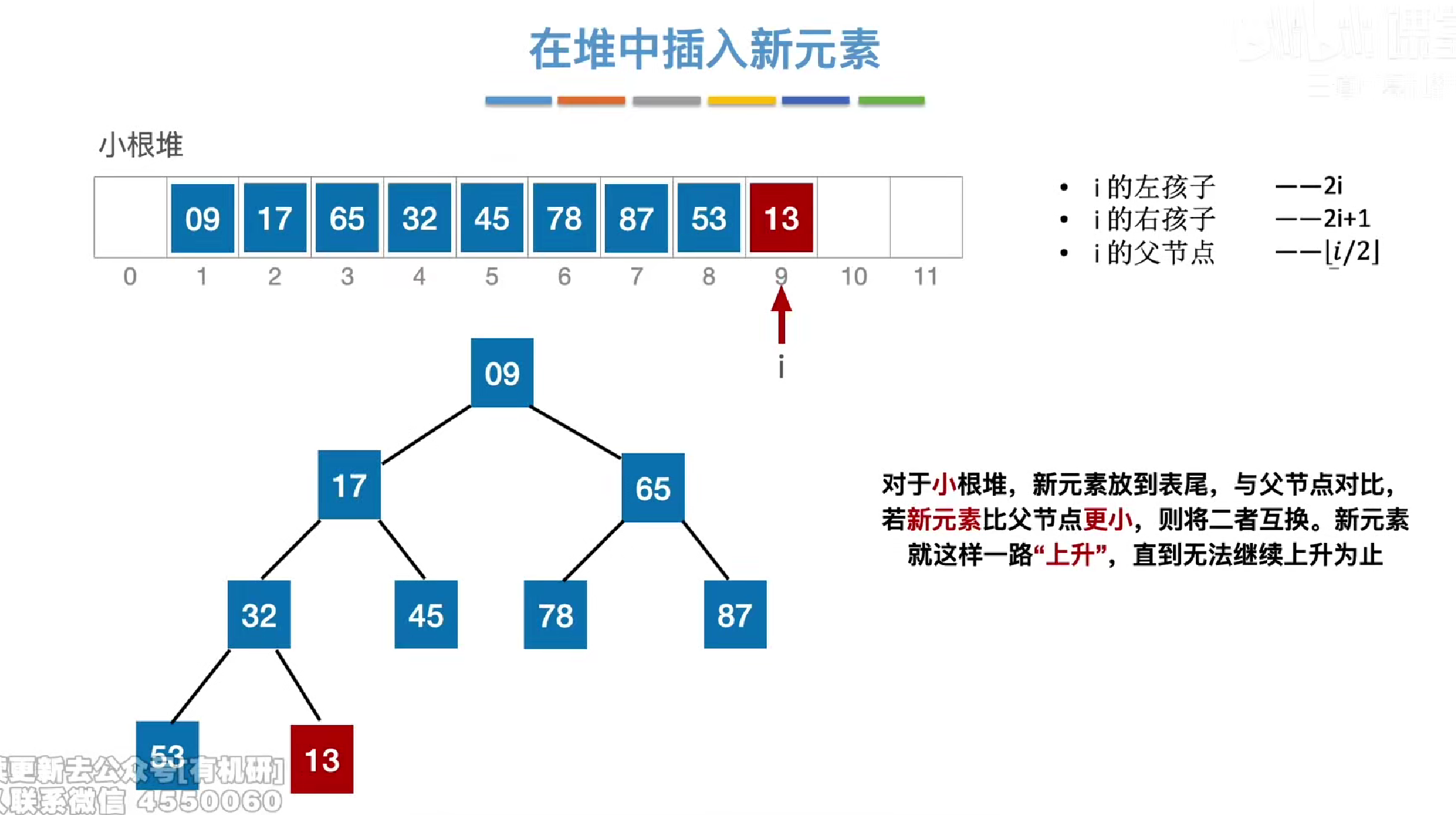
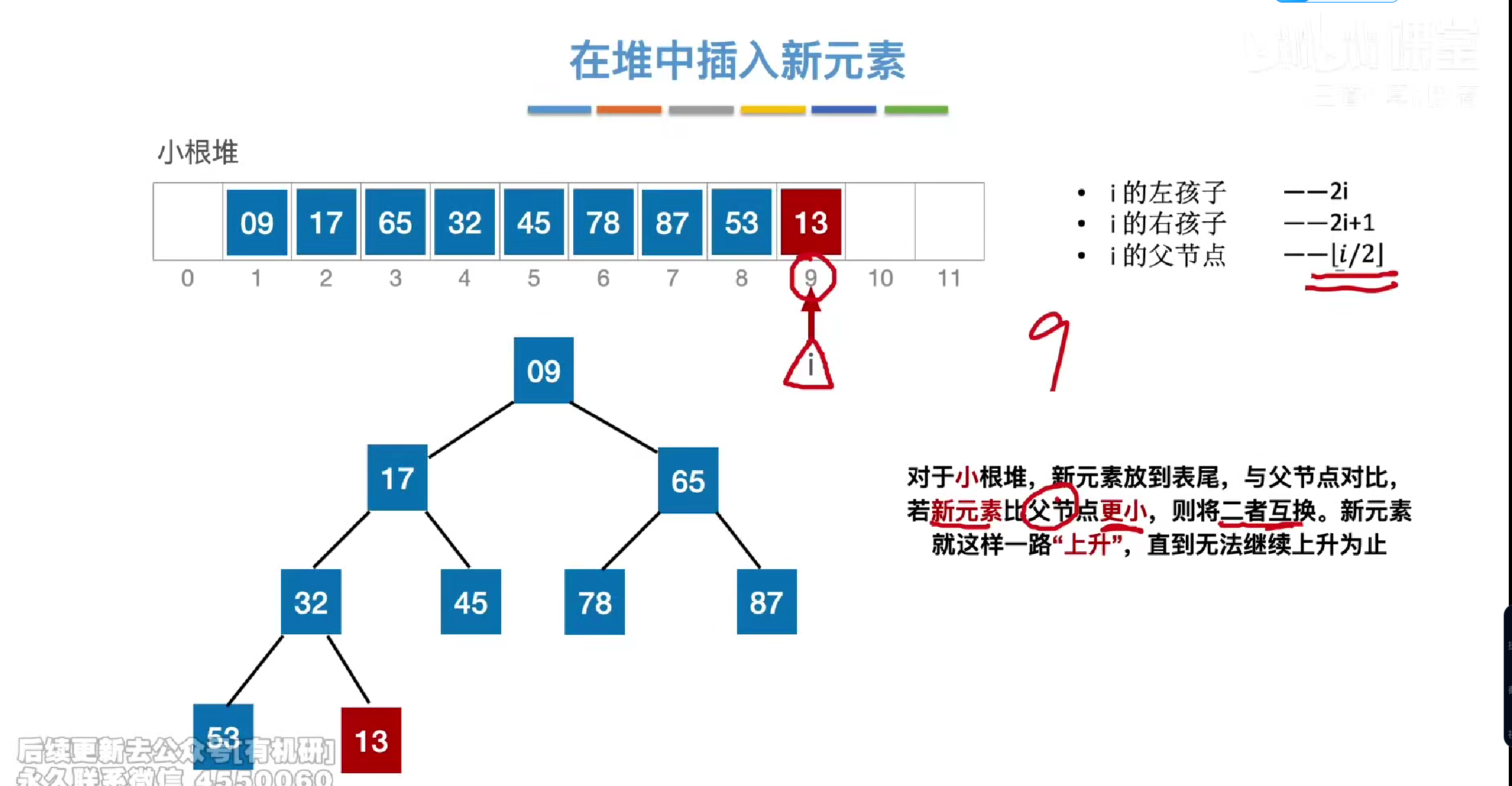
堆的插入
首先插入表尾
删除元素
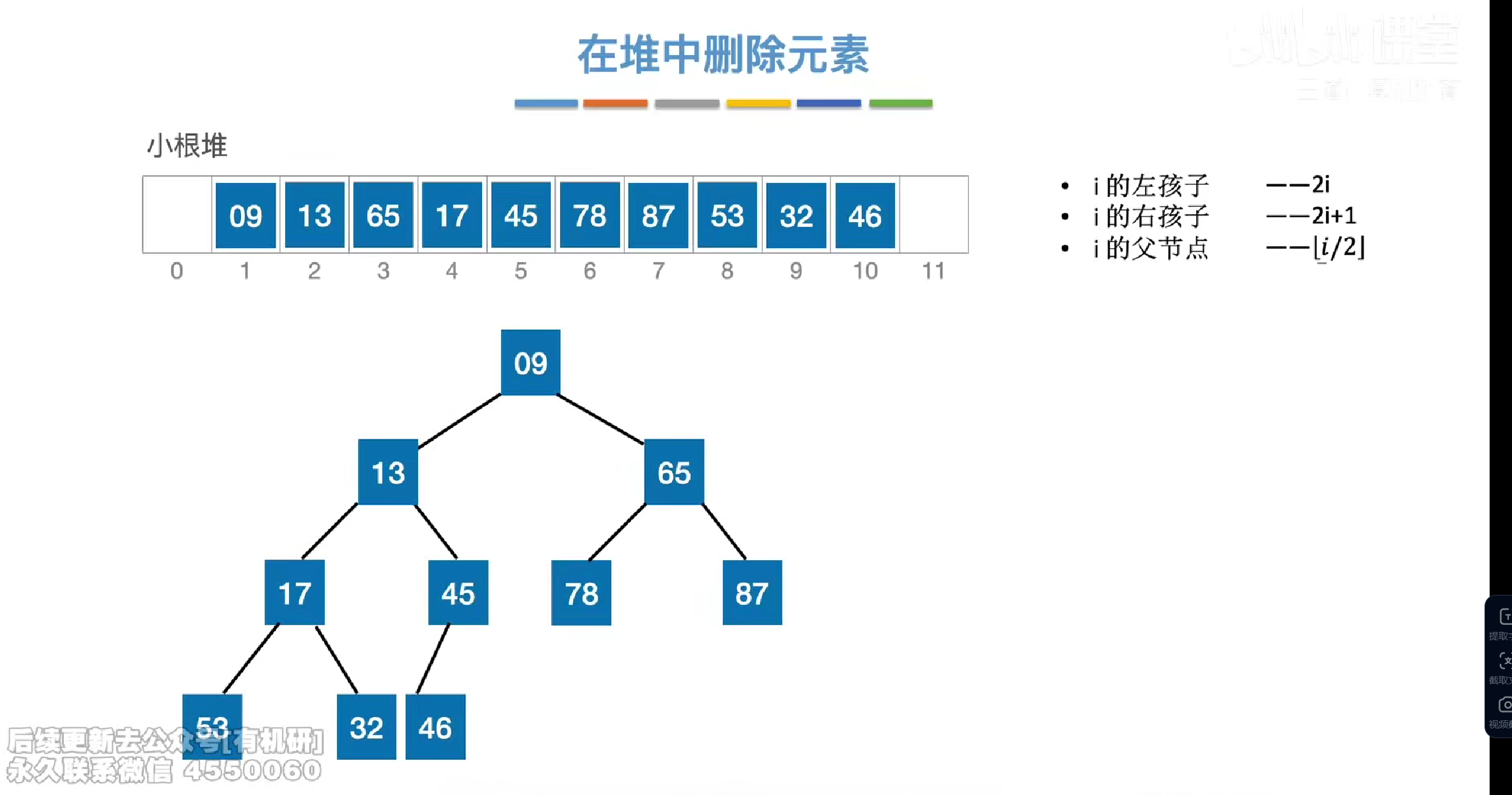
元素被删除后我们会采用堆底的元素代替被删元素
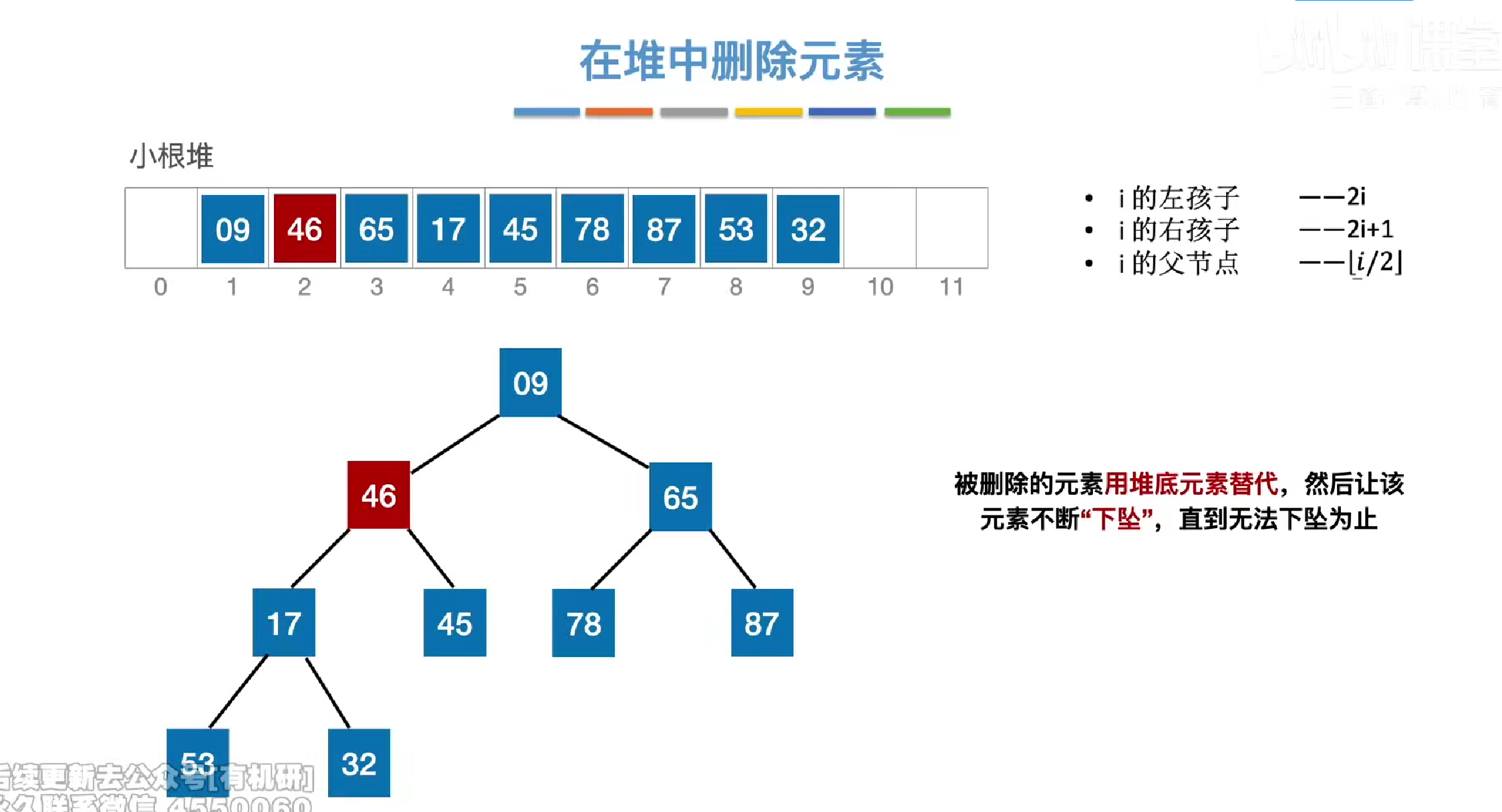
然后在对元素是否符合堆的定义进行互换保证正确性
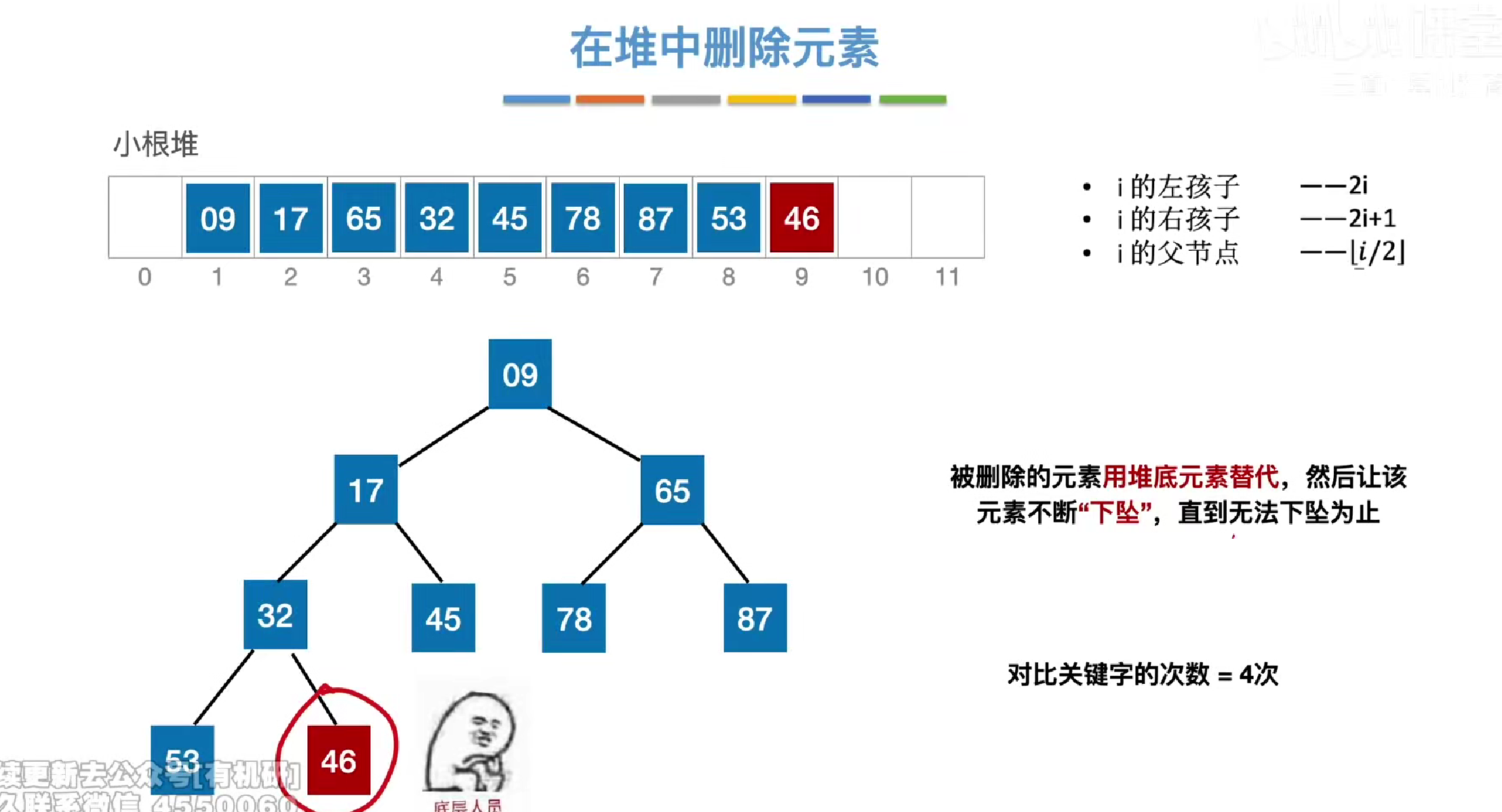
关键字对比次数
每一次下坠大都会现在子节点中找到更小/更大的子节点
然后再用父节点对比更小的子节点观察是否发生交换
即两次对比
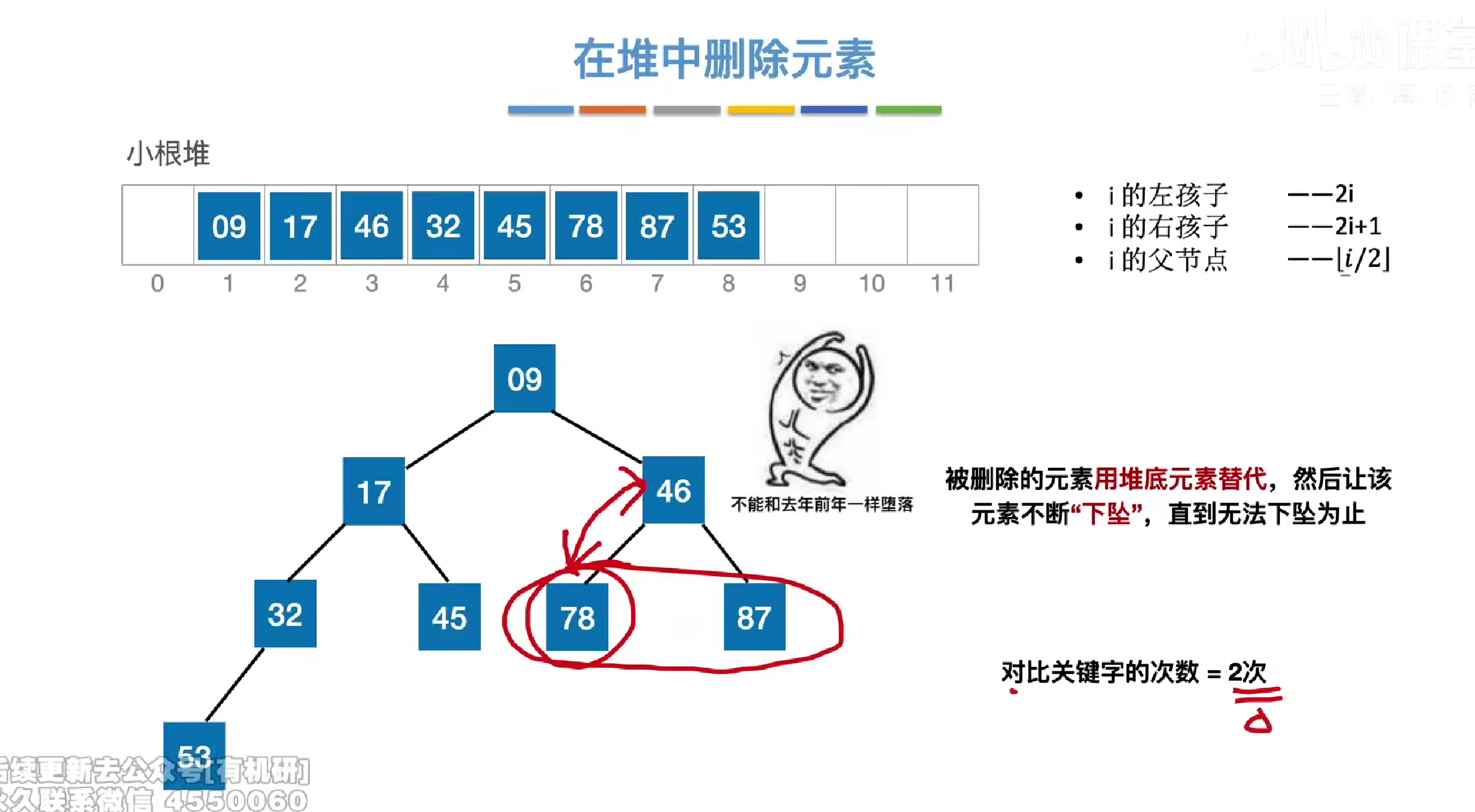
总结
归并排序

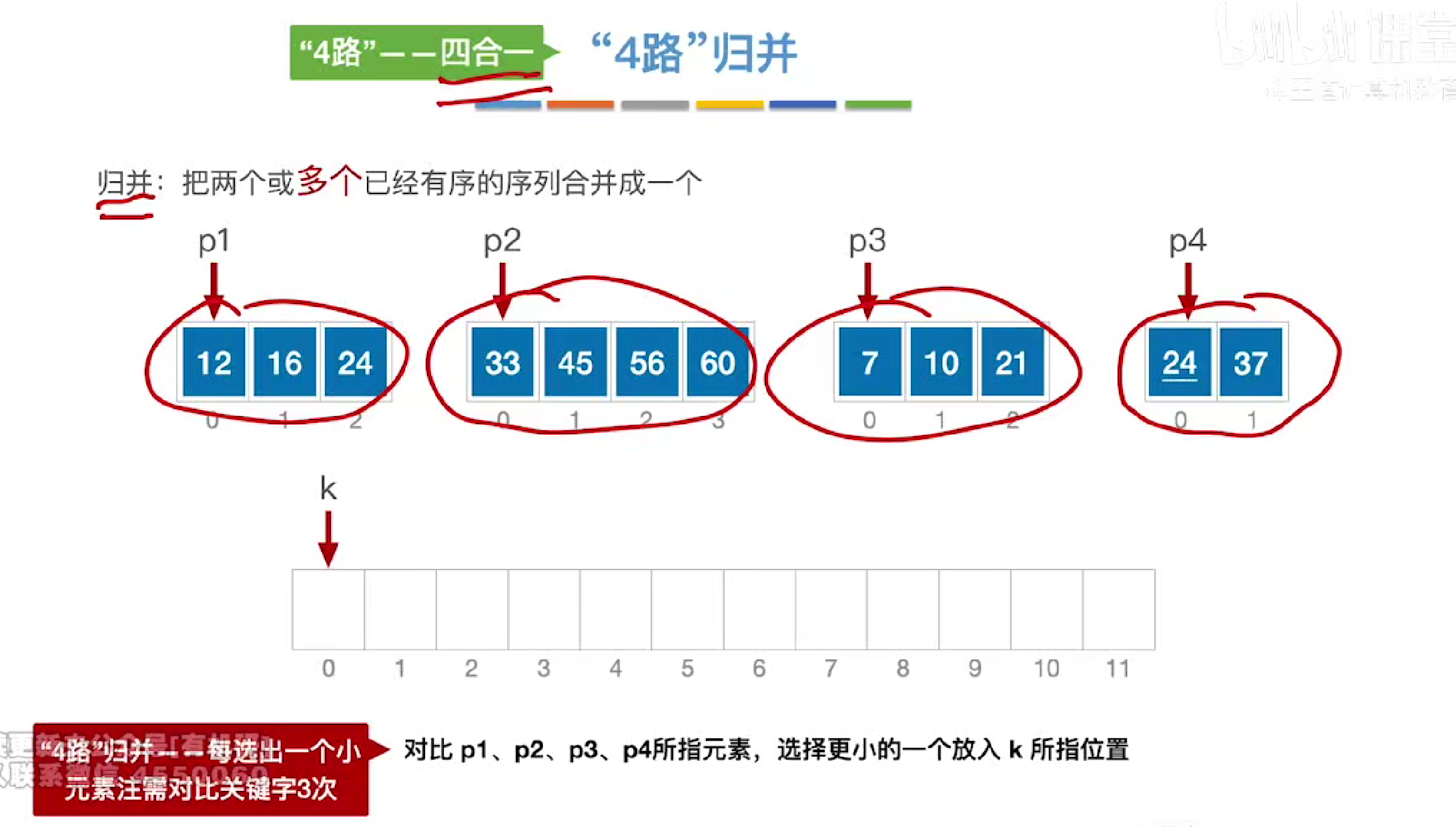
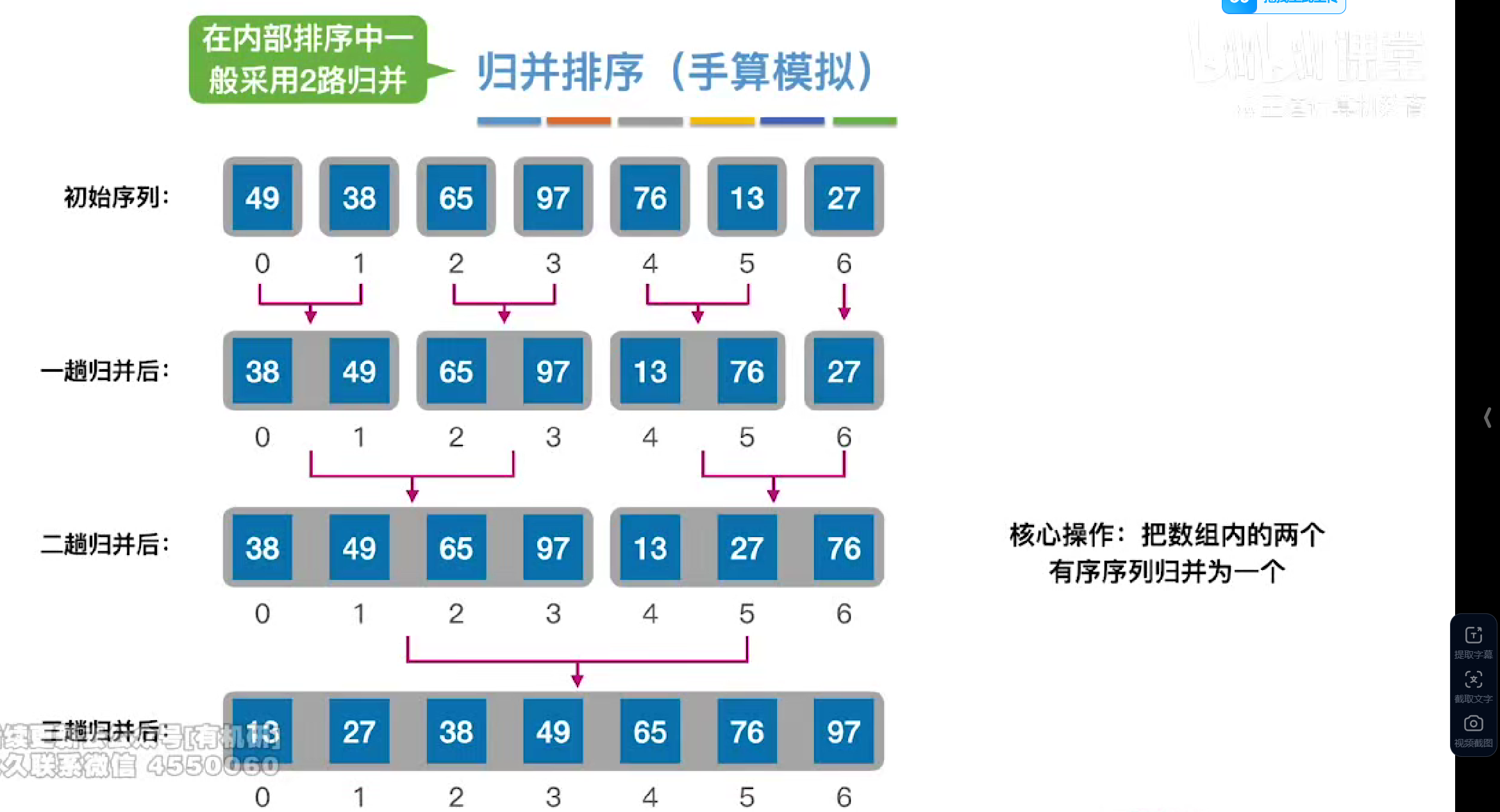
过程
递归实现
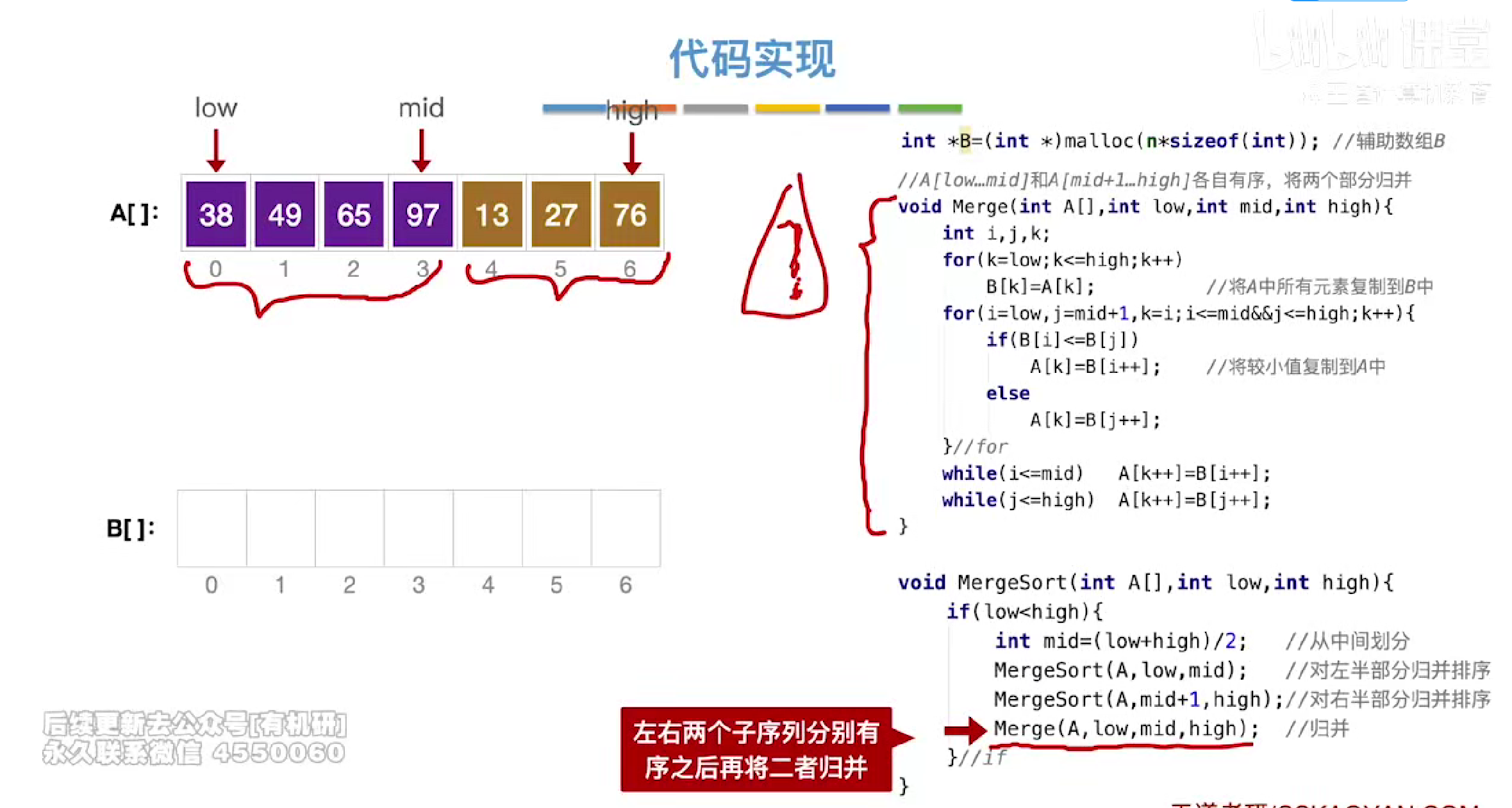
代码实现
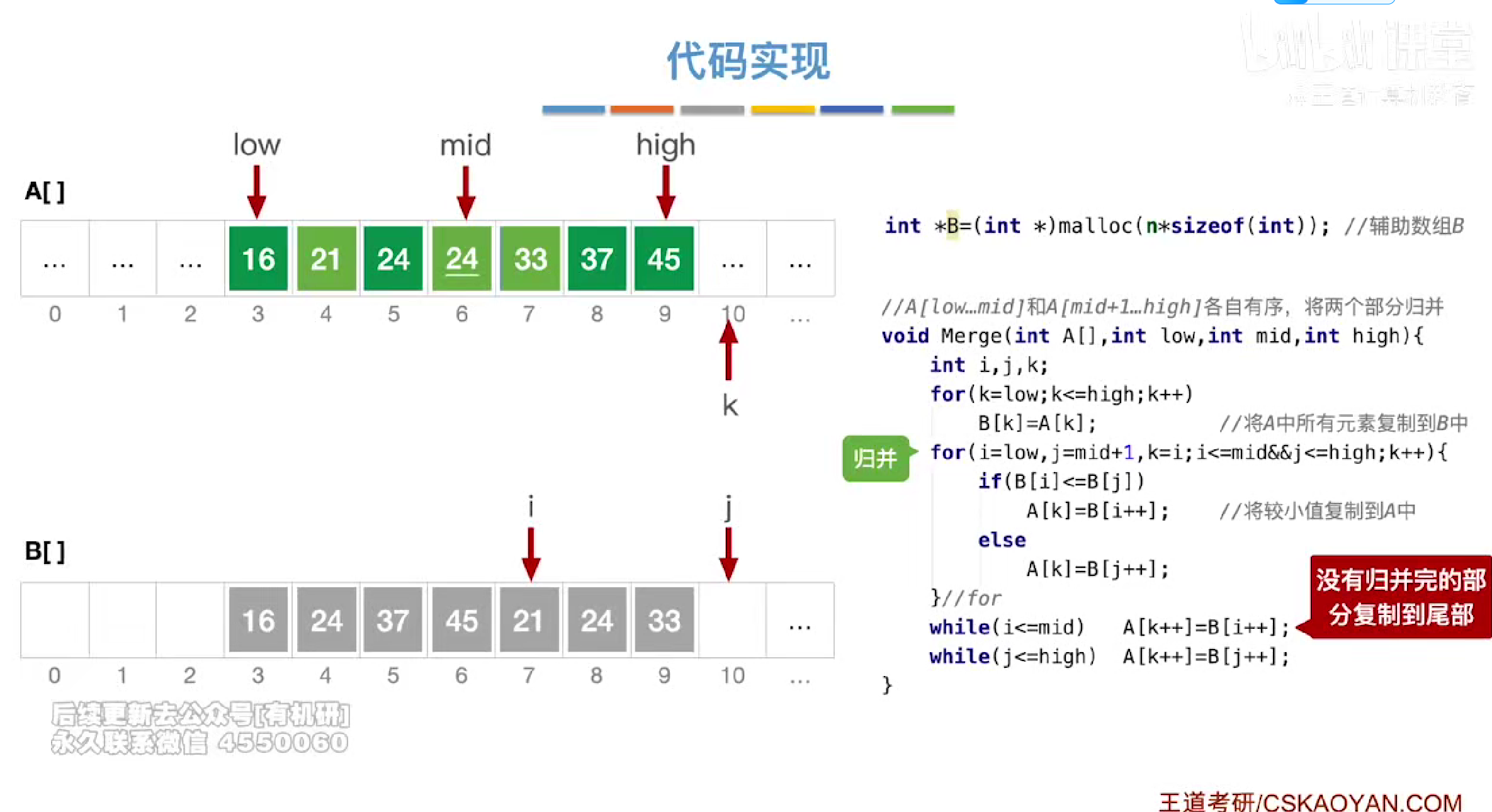
其中low是第一个序列的起始位置,mid是第一个序列的结束位置,high是第二个序列的结束位置,
因为两个序列是连着的所以才能这样归并
定义一个辅助数组b将所有元素装入其中,然后按照归并的定义和边界判断条件进行归并排序排序,放入原本的数组A中
递归实现,一路向下进行递归直到数组为1,然后跳出最底层的递归函数开始对倒数第二的序列进行递归排序
时空复杂度
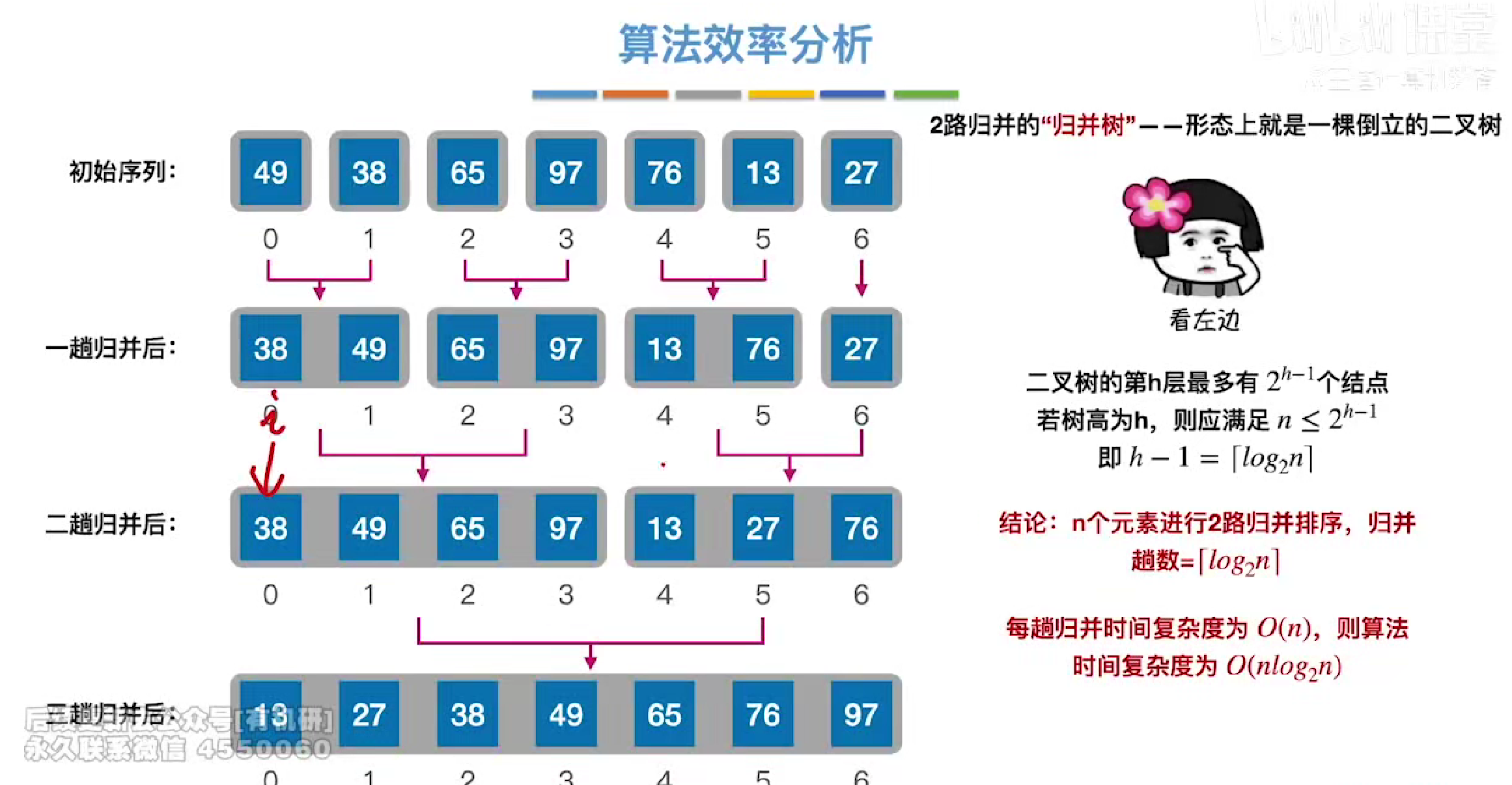
最好最坏都是onlog2n
并且归并的次数=h-1
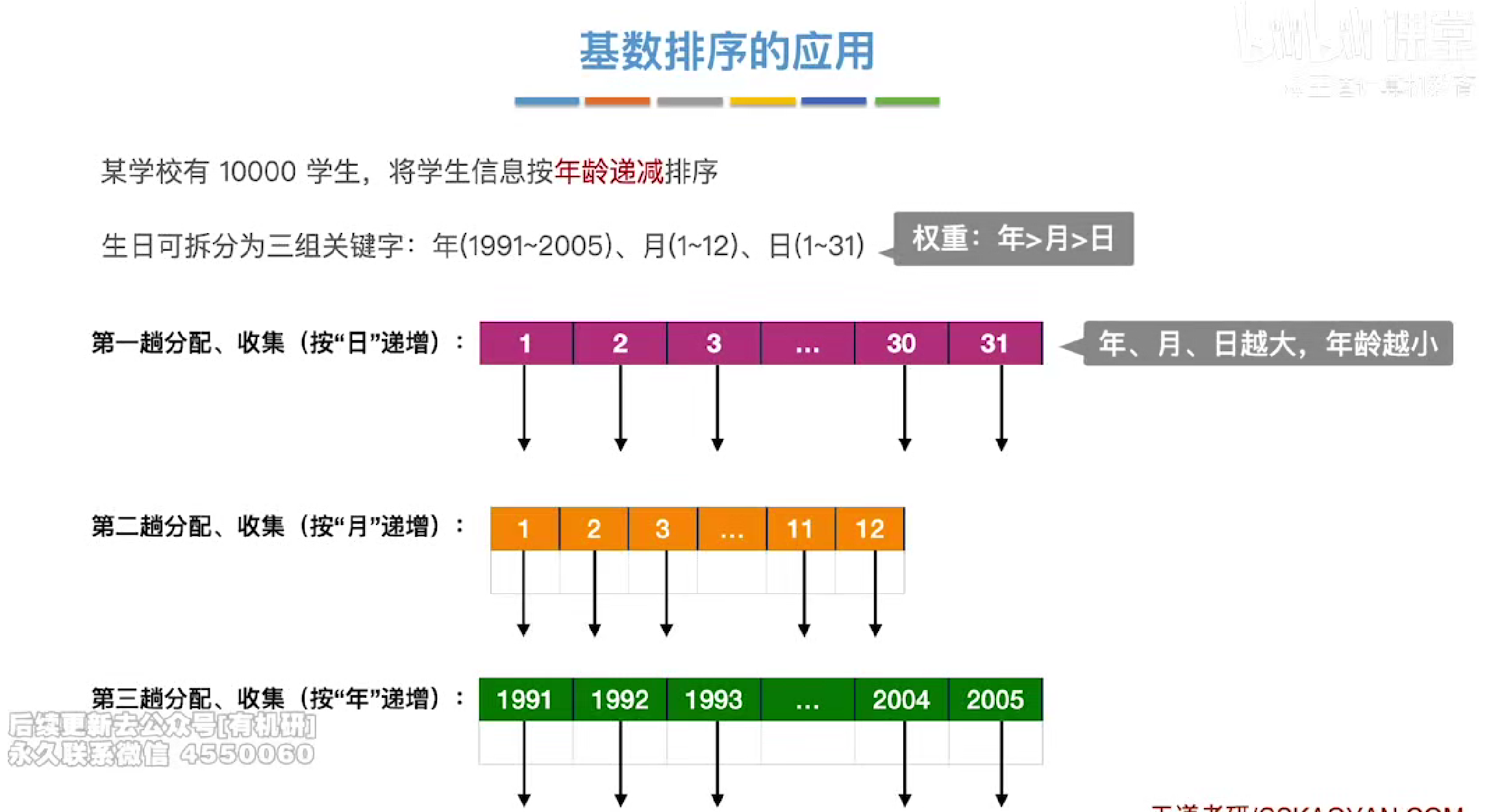
基数排序
实例

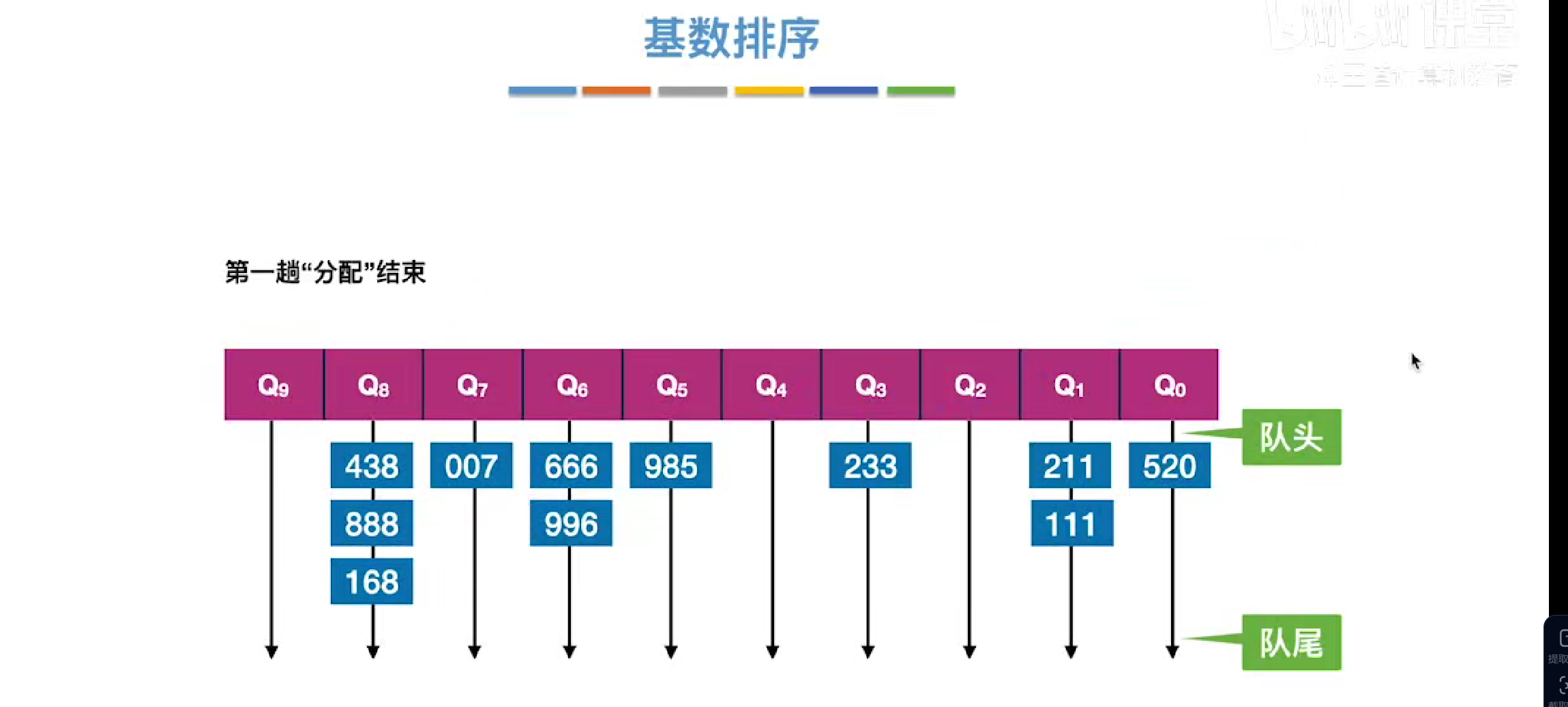
先按照个位数进行队列元素的分配,并用链表串起来
然后按照递减的顺序(因为我们想得到的是一个递减序列)
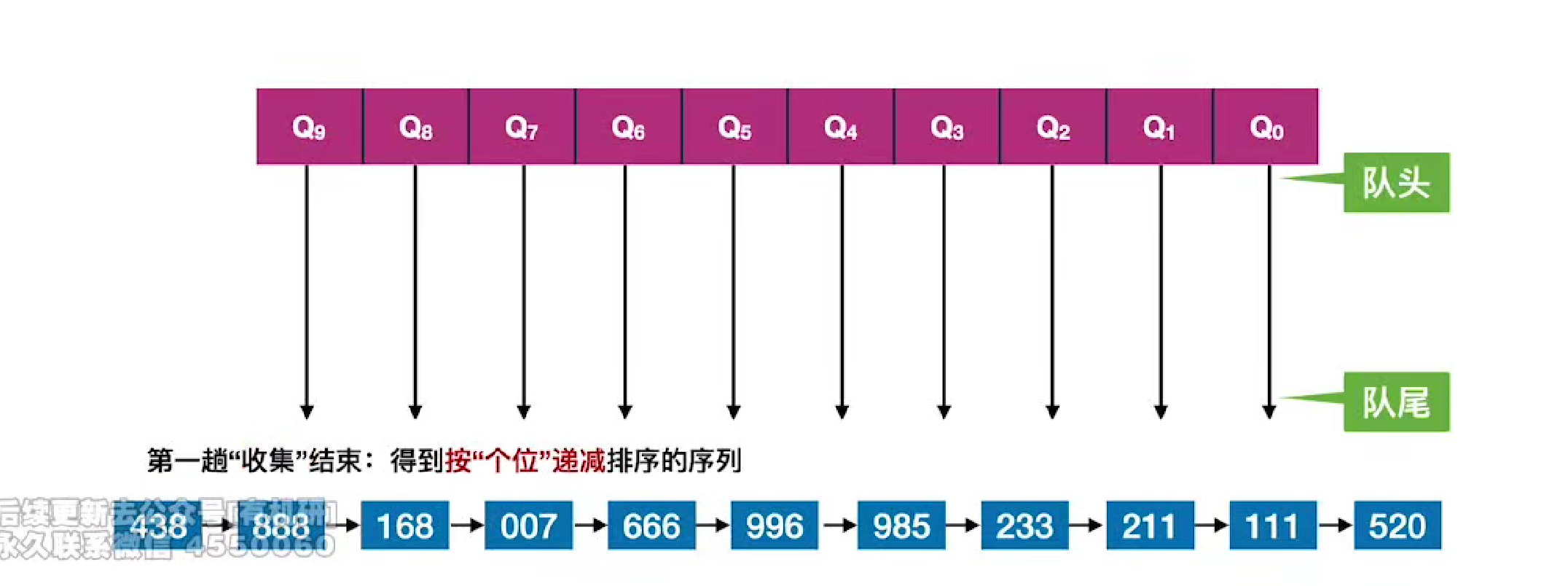
第二趟
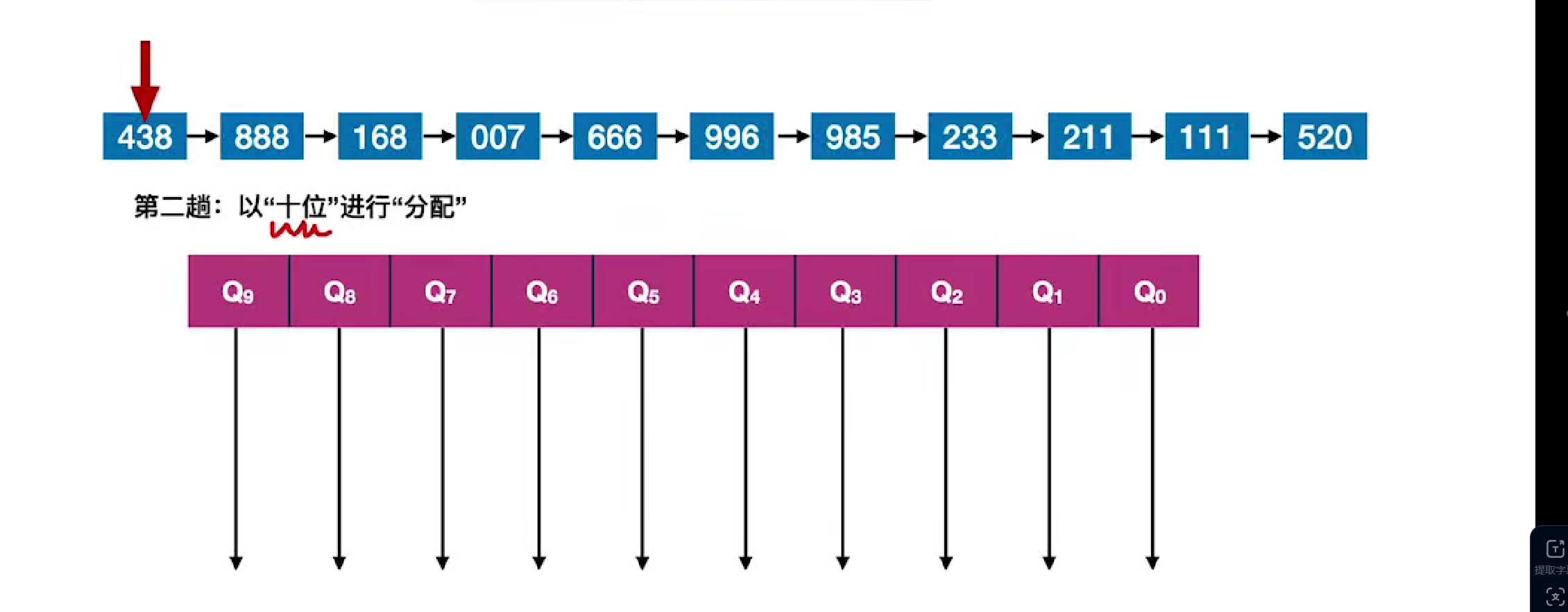
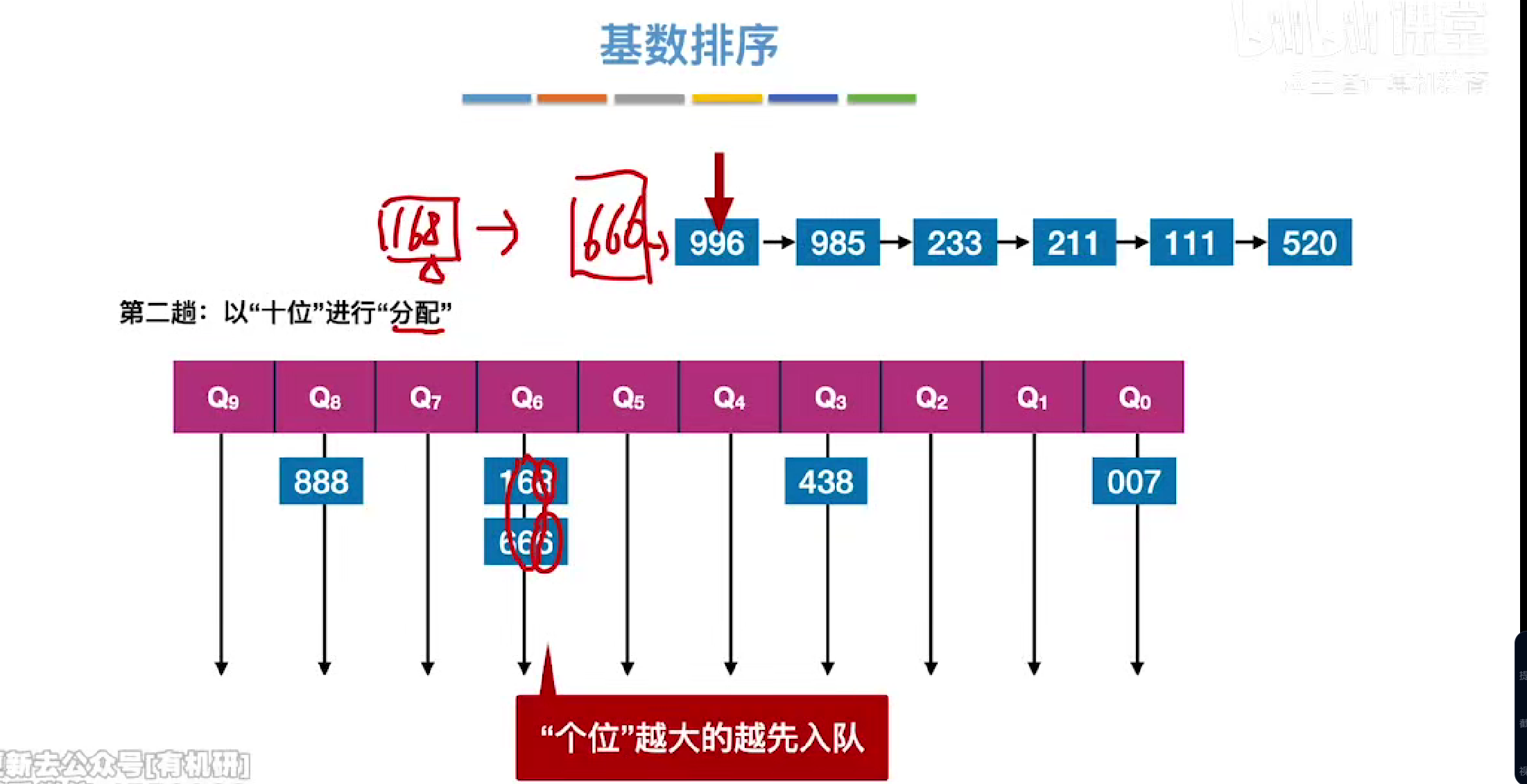
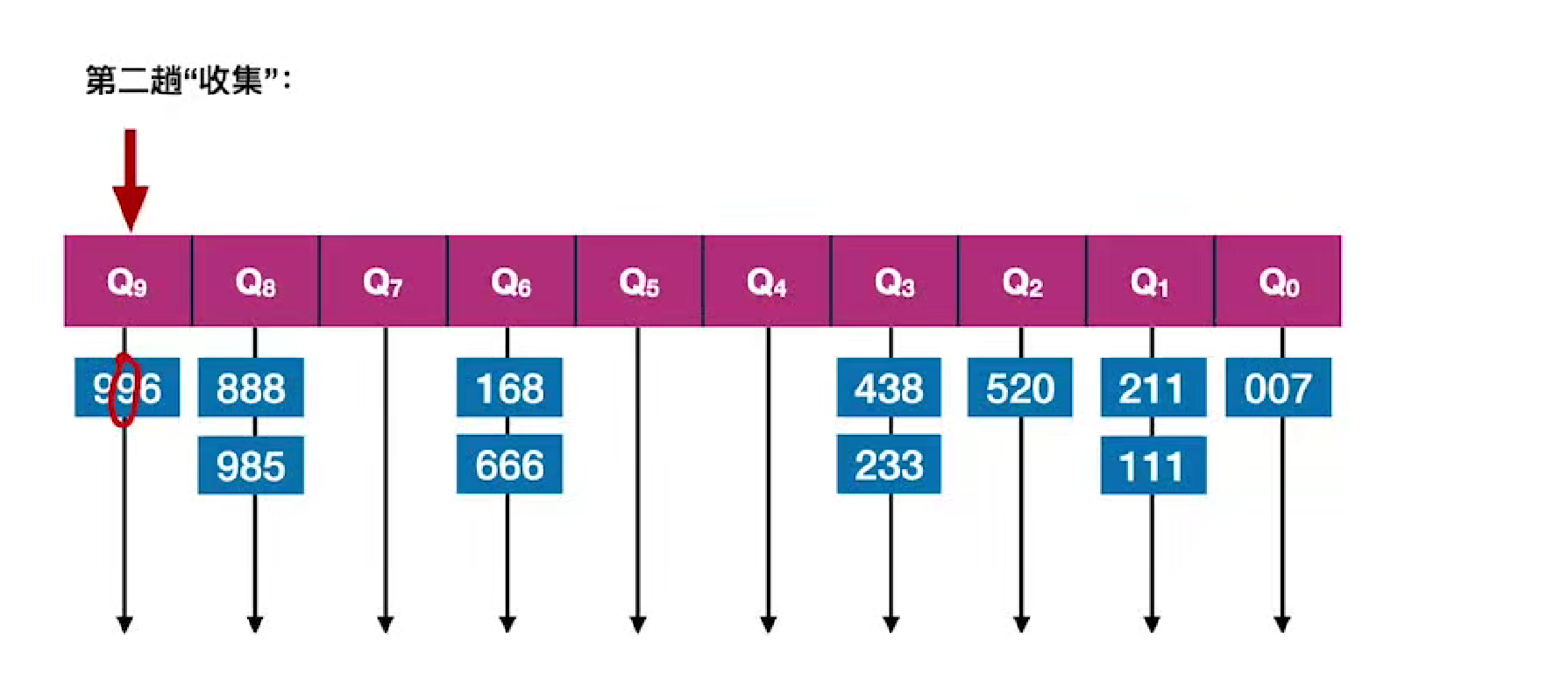

第三趟
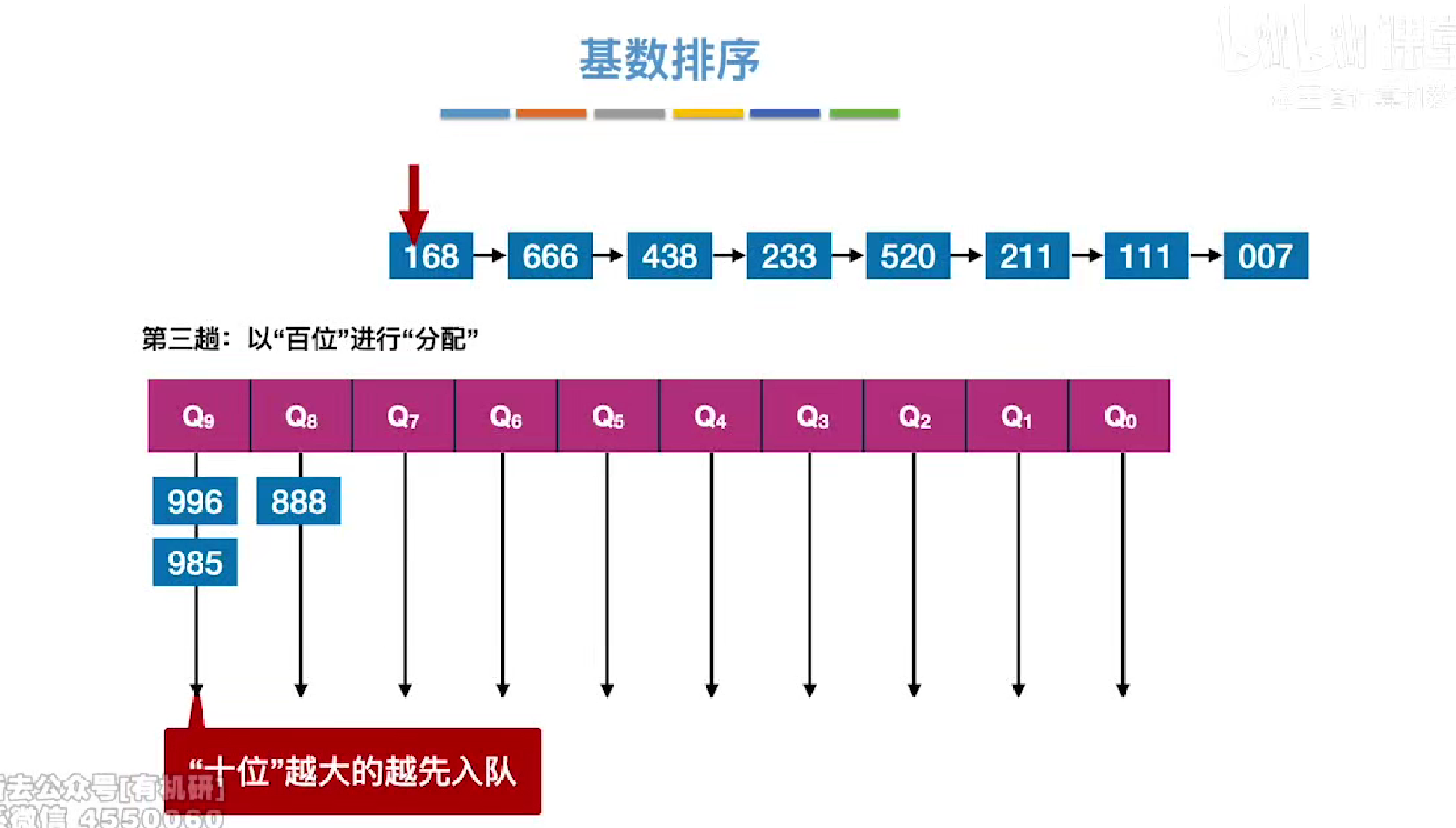
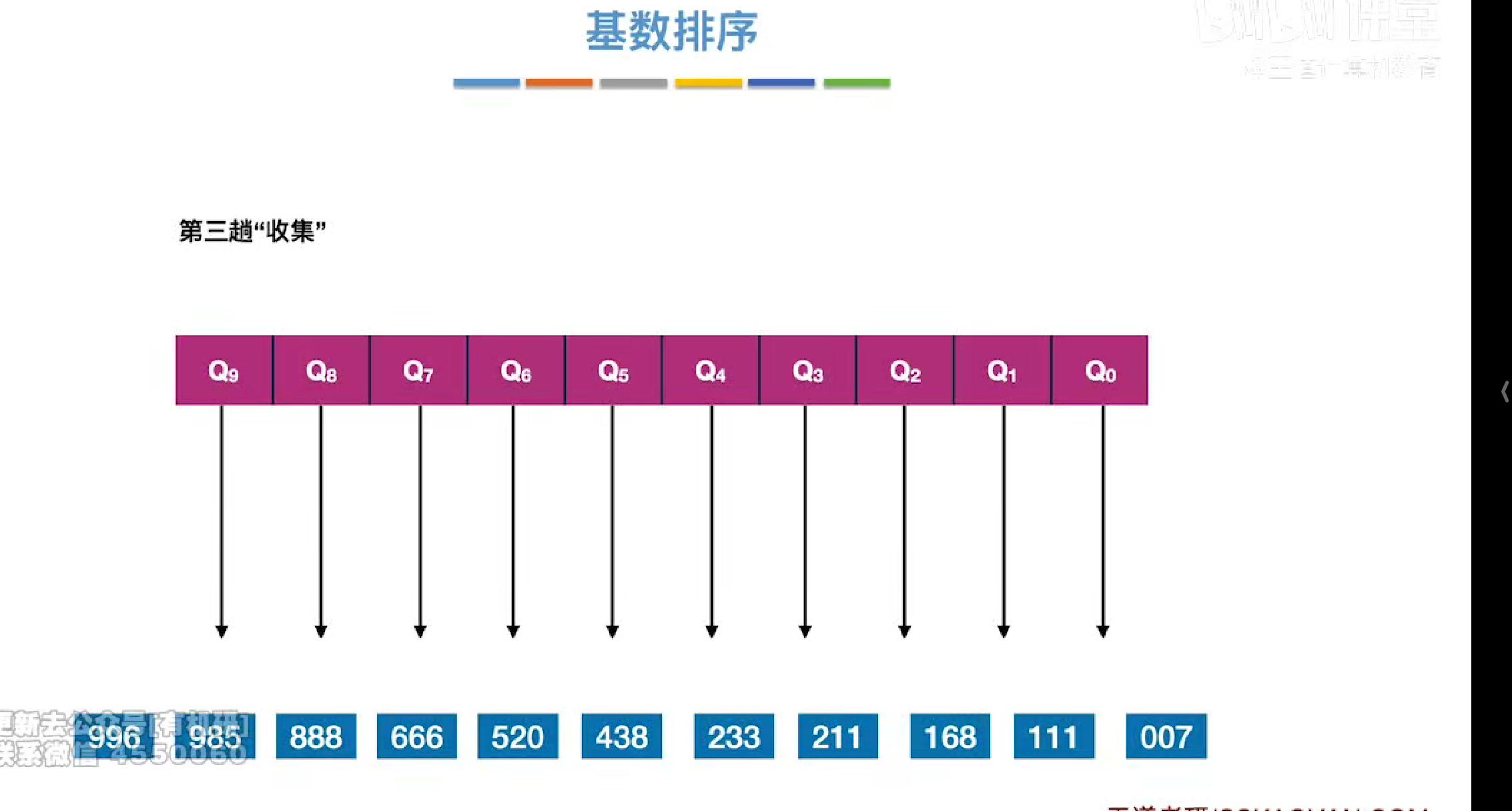

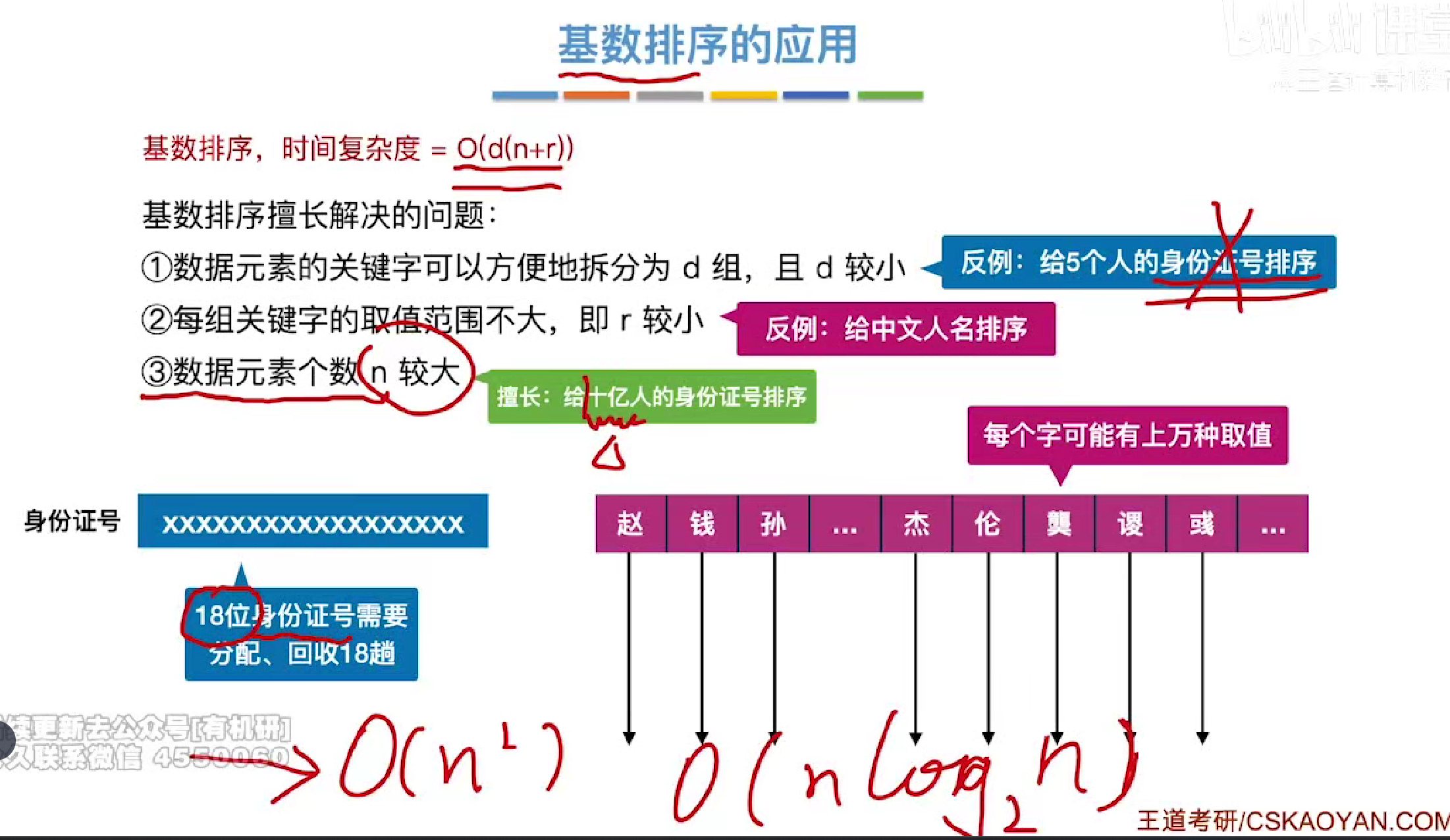
方法
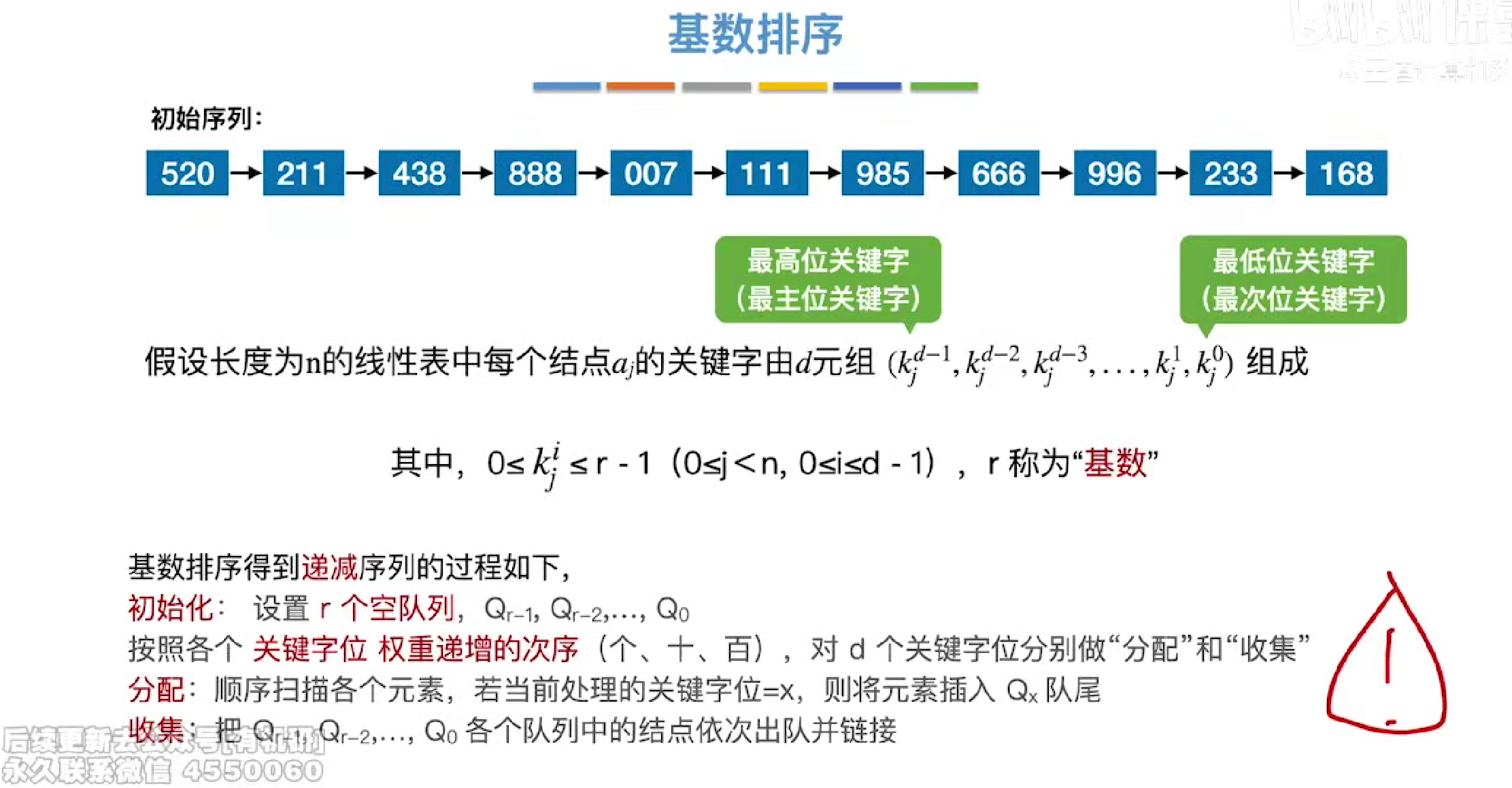 时空复杂度
时空复杂度
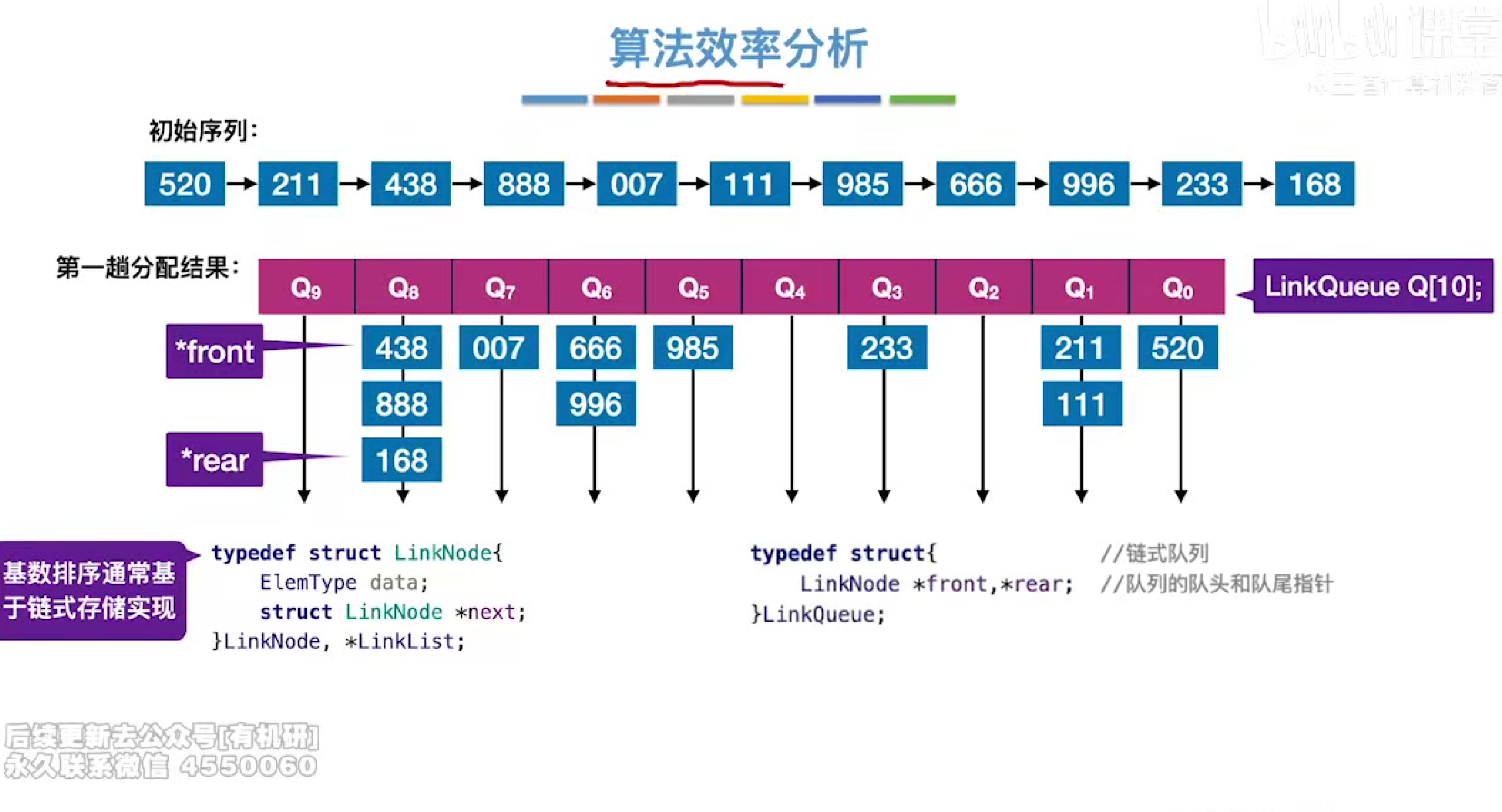
r是关键字分了多少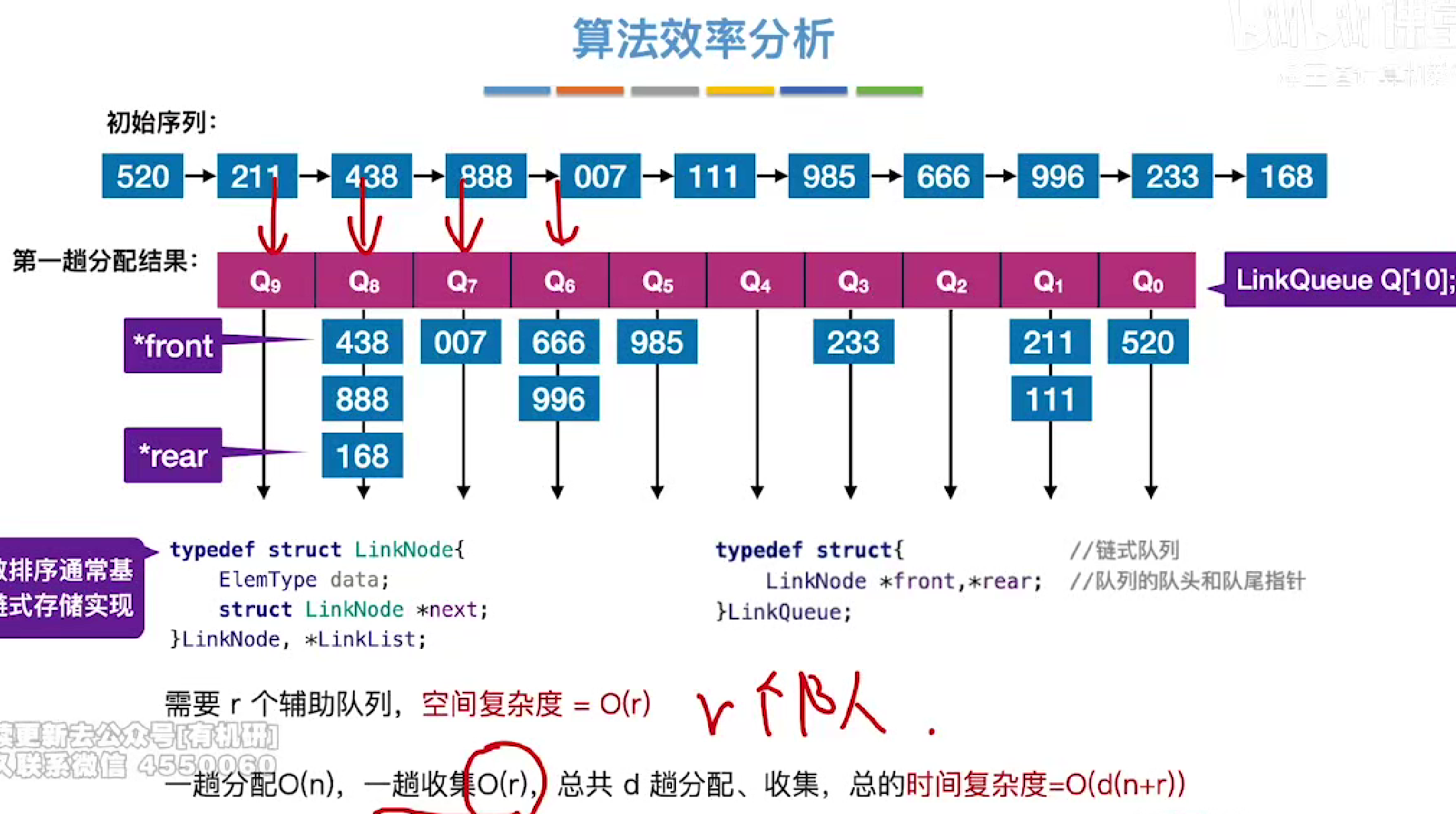
应用

计数排序(考纲不做要求,但是思想重要)
算法思想
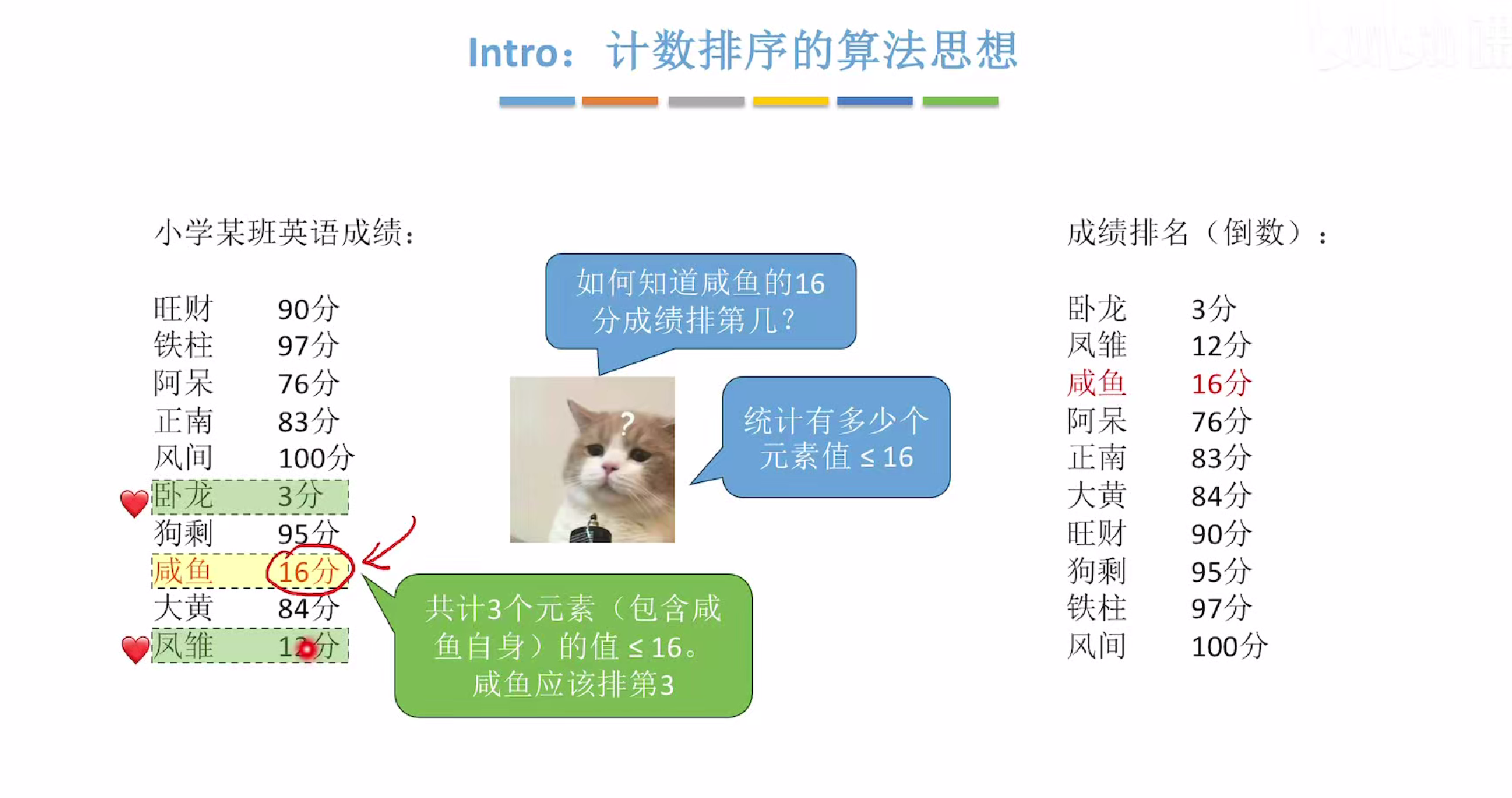
相当于哈希算法,记录关键字出现的顺序进行排序
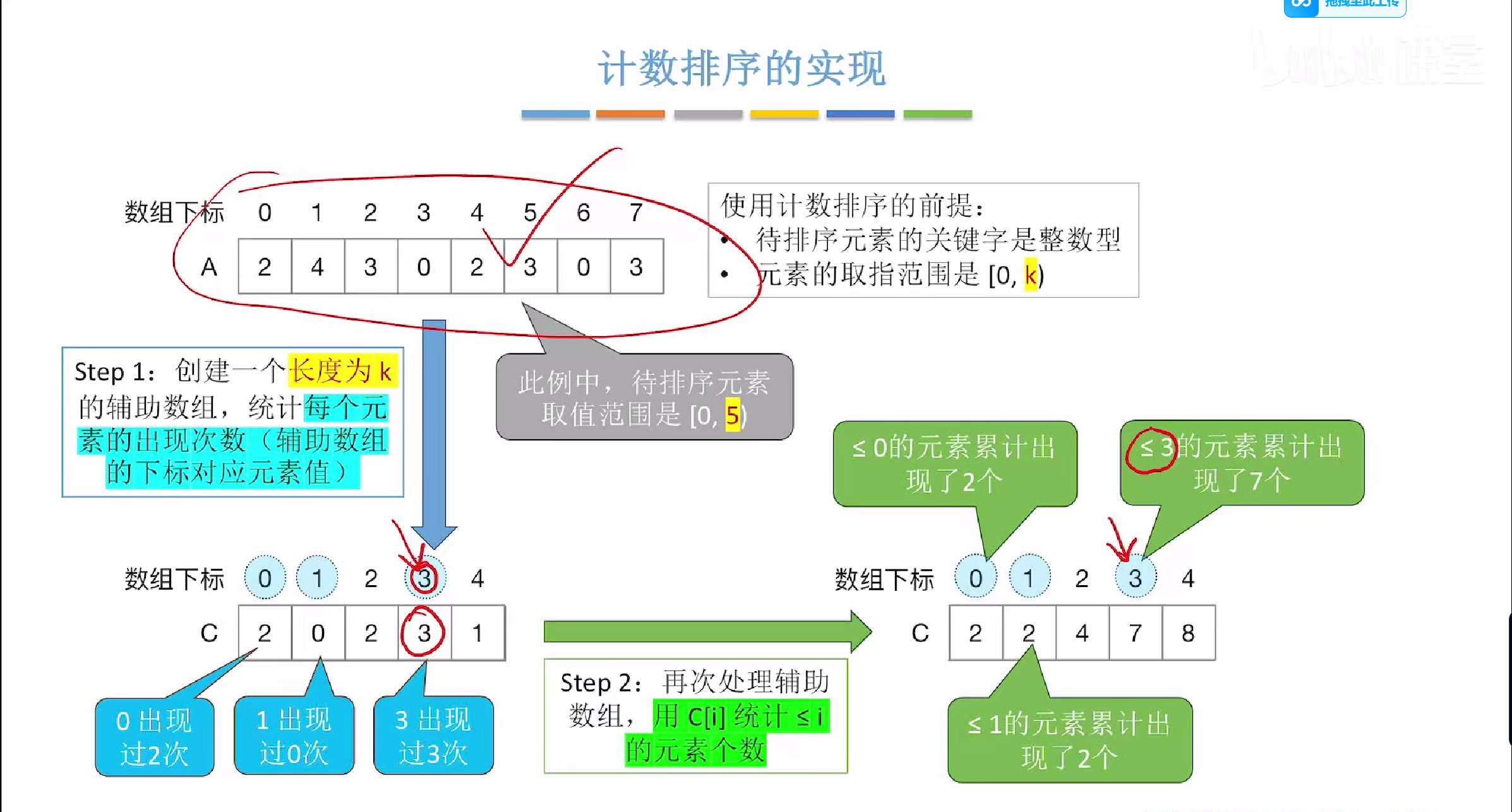
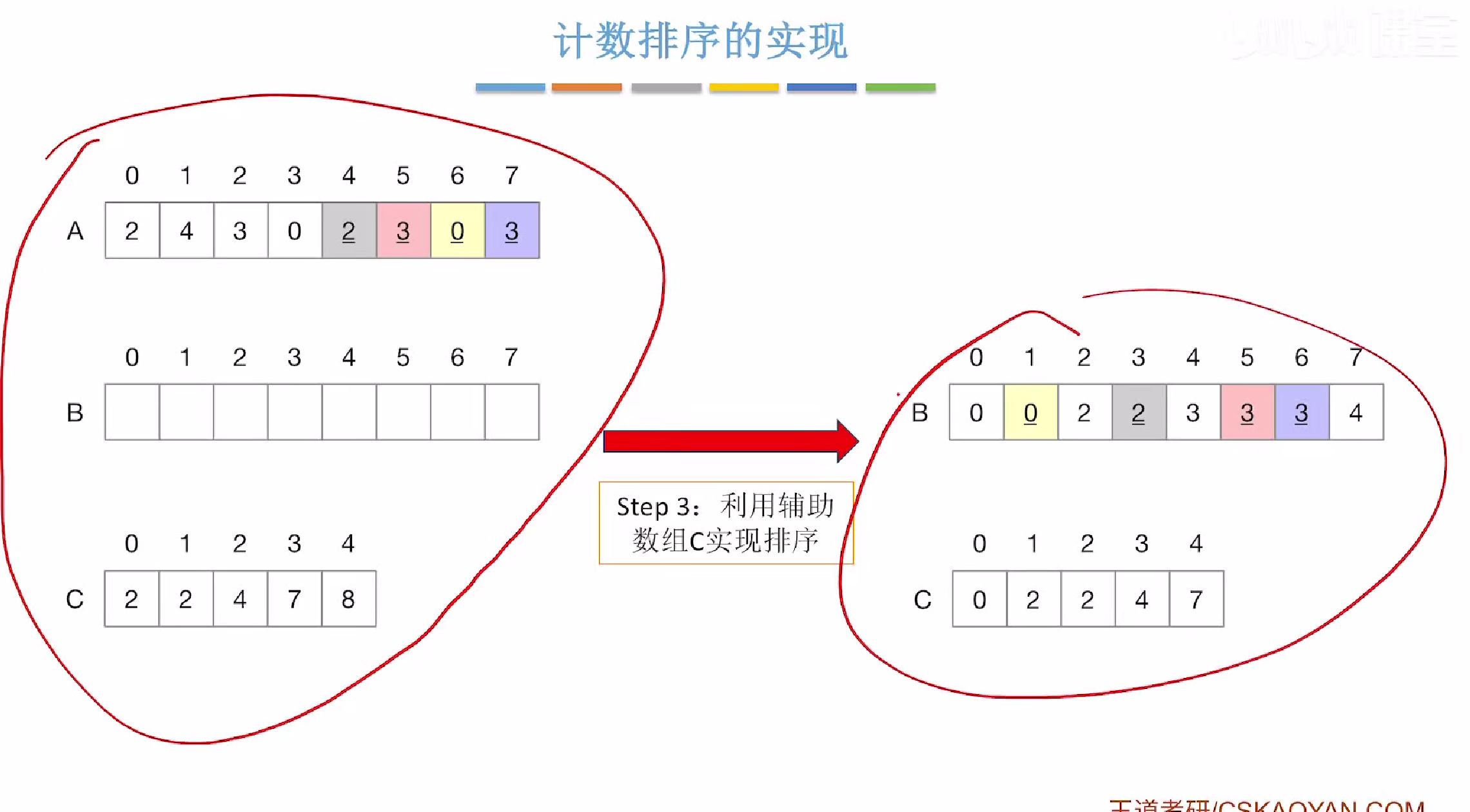
具体过程,我们遍历数组,先从后往前遍历
第一趟:我们发现关键字3出现的次数是7,代表着前面有七个元素<=3,那么也就意味着,3应该放到第七个位置,然后我们在对c中的3进行减一操作,代表着已经有一个3被放入到排好序的数组中
但在代码实现中,我们是先-1,得到6然后再放入对应的B组下标中,这样方便代码的书写
第二趟:我们发现关键字是0,所以我们找到c中对应的关键字0的次数是2,所以有两个元素<=0所以放入第二个位置,也就是数组下标为1的位置
所以以此类推进行排序
时空复杂度
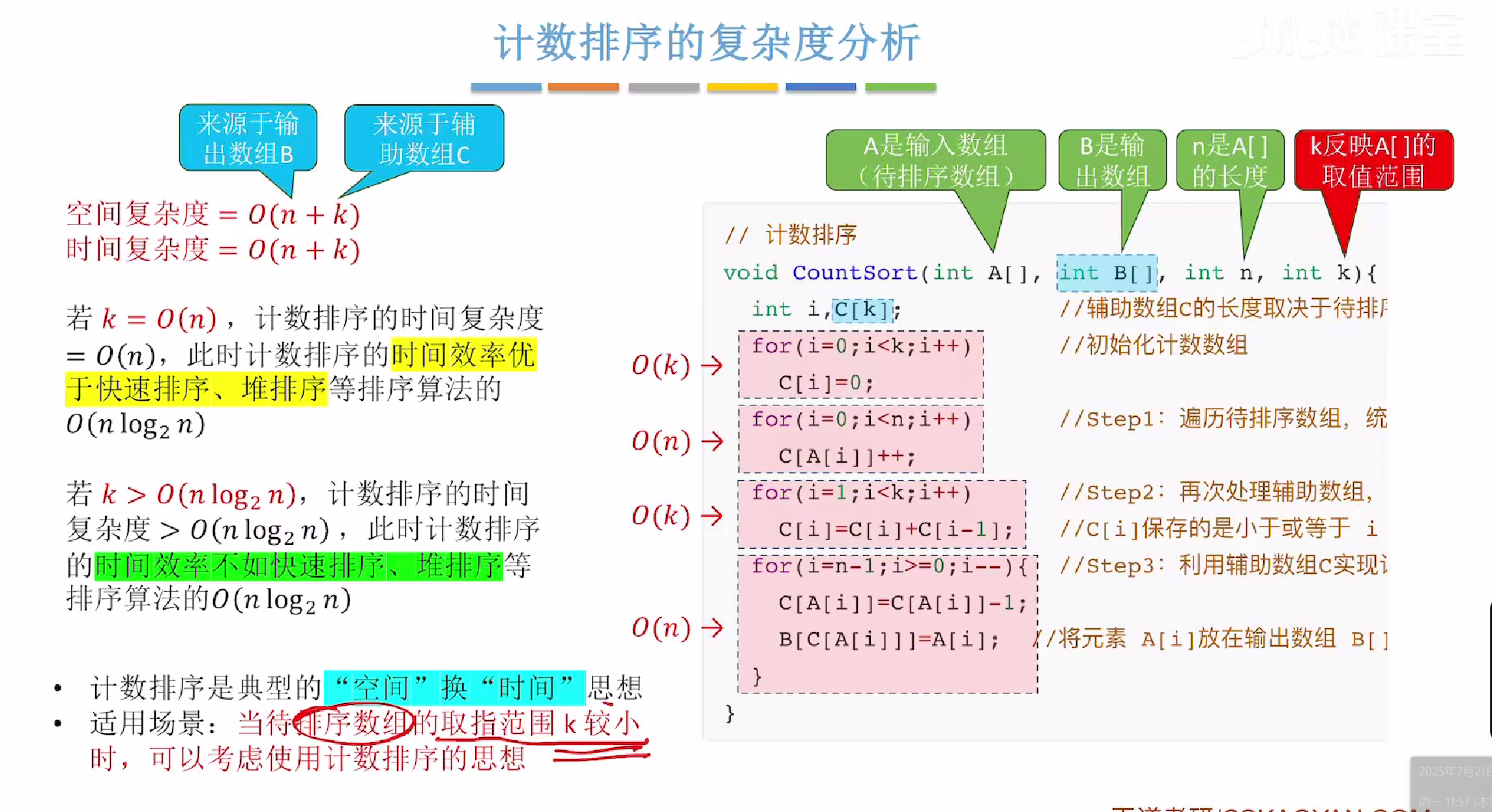
总结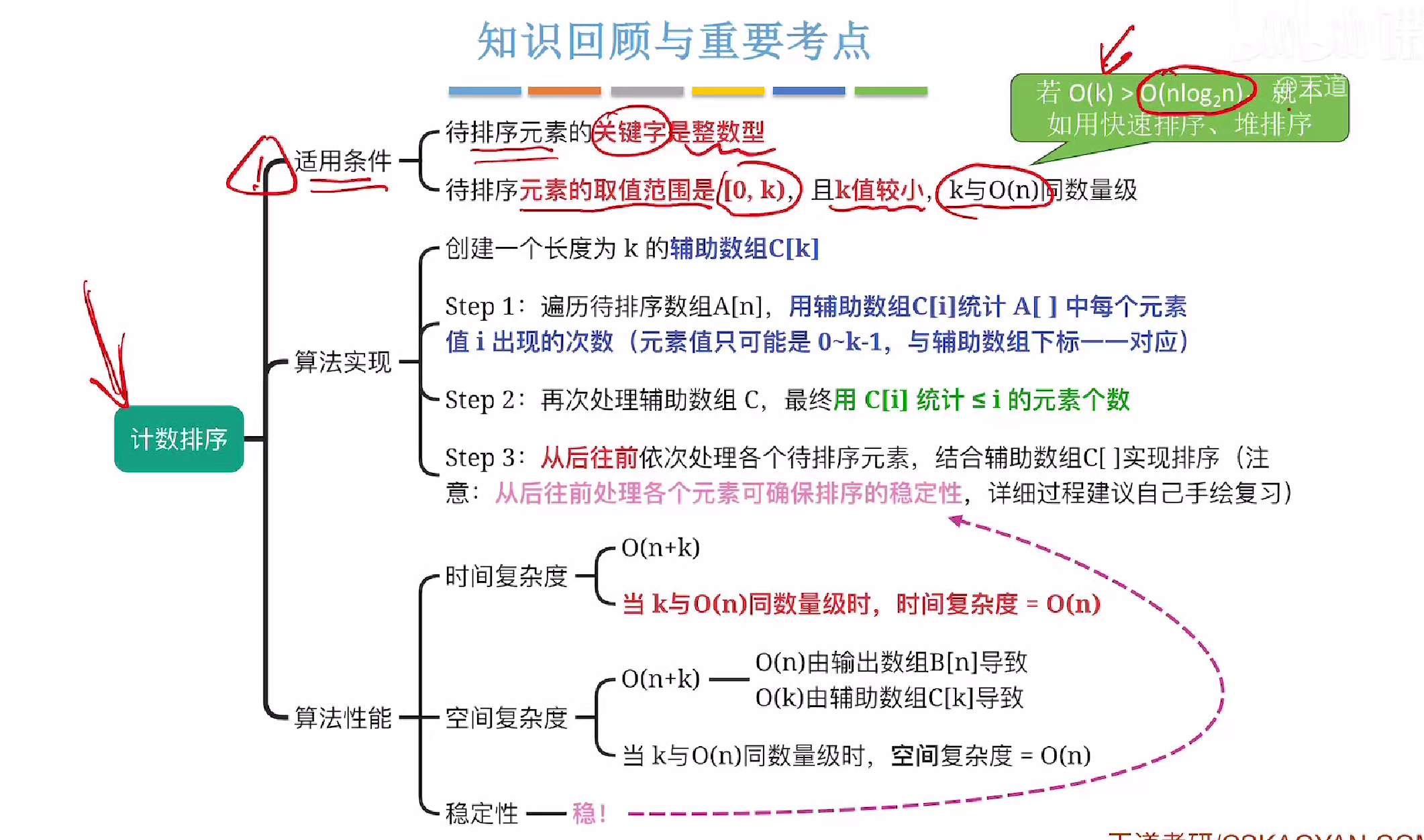
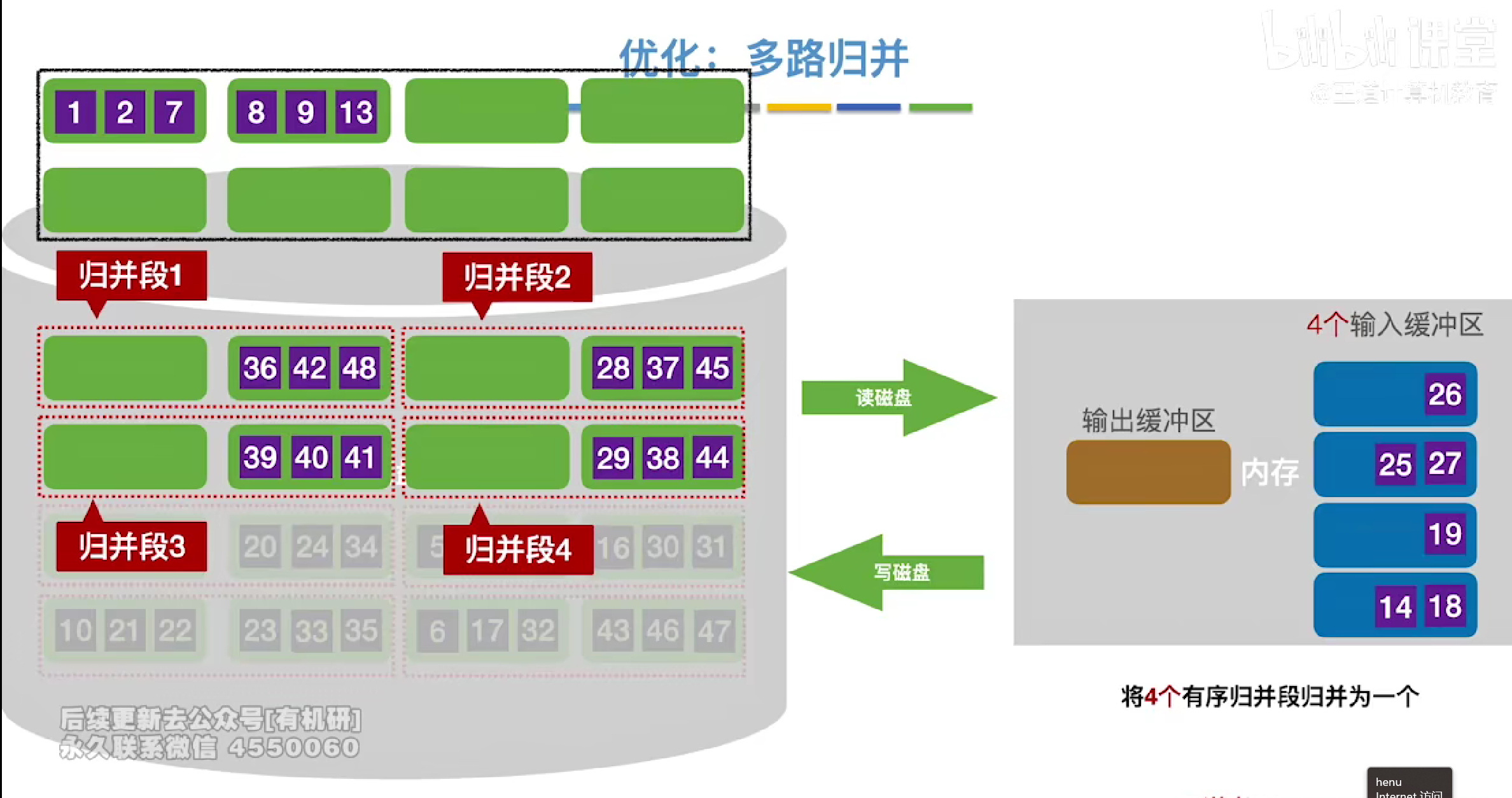
外部排序
每次以块为单位读取
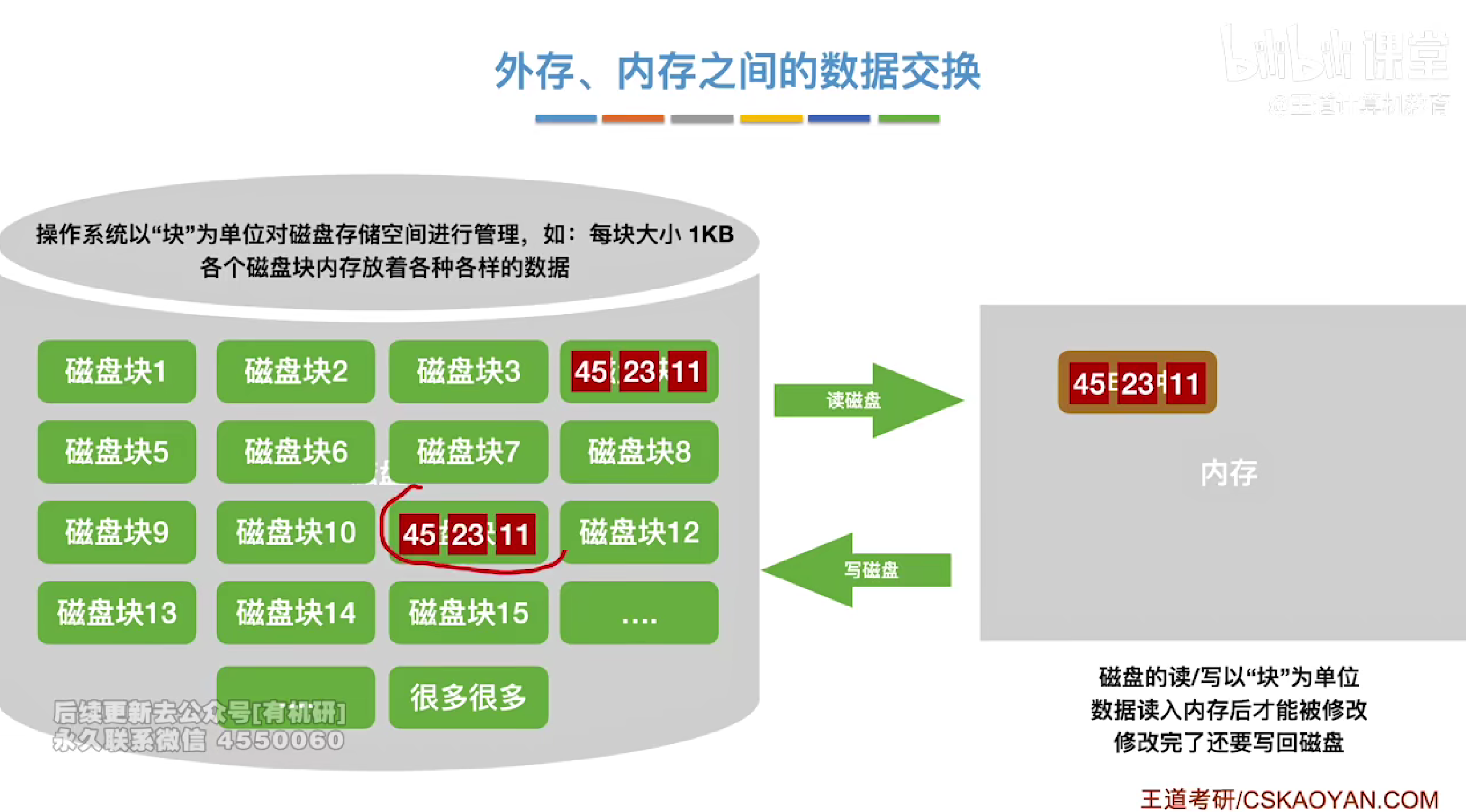
再内存中进行内部排序整体有序之后构造归并段
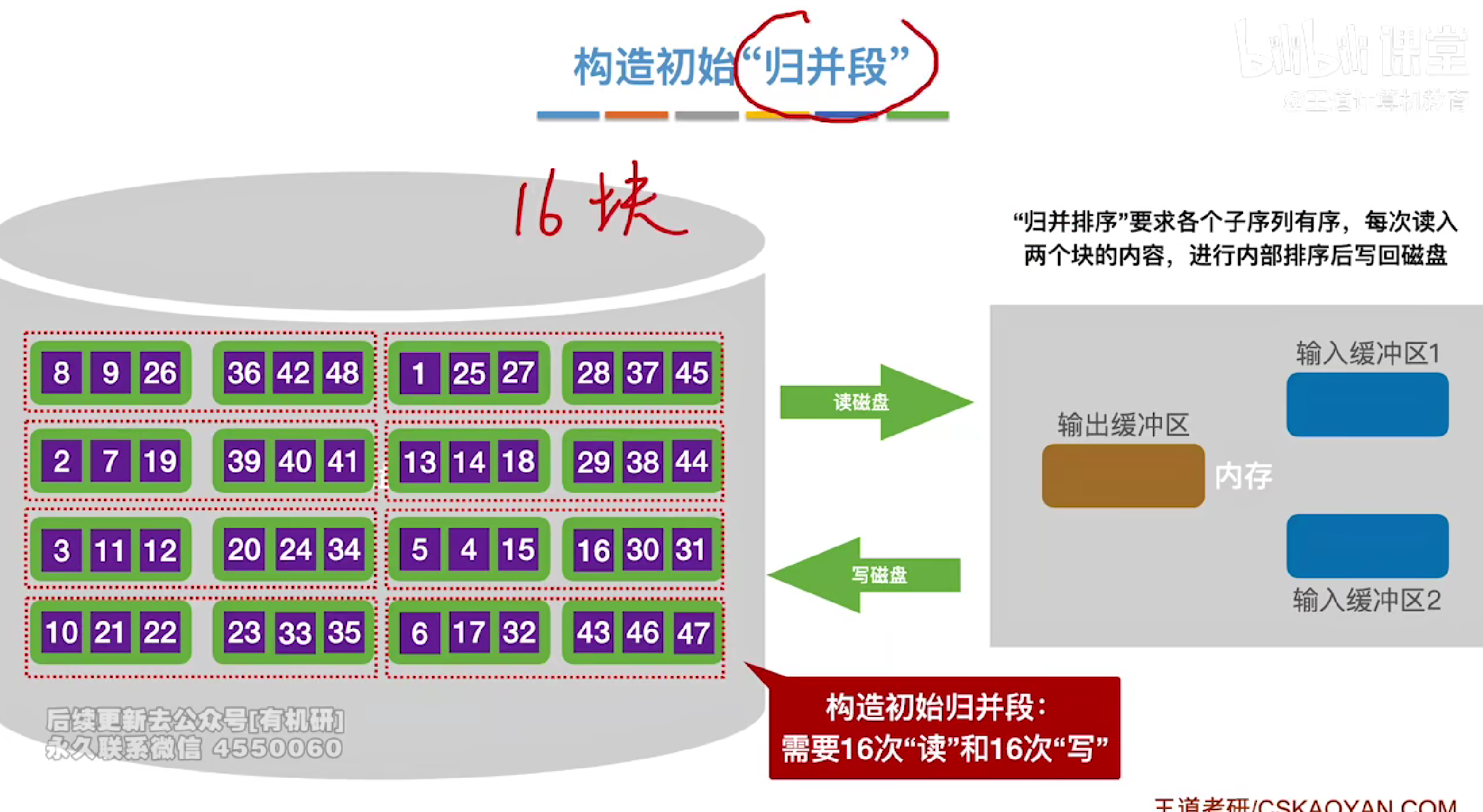
挑选两个进入输入缓冲区进行归并构造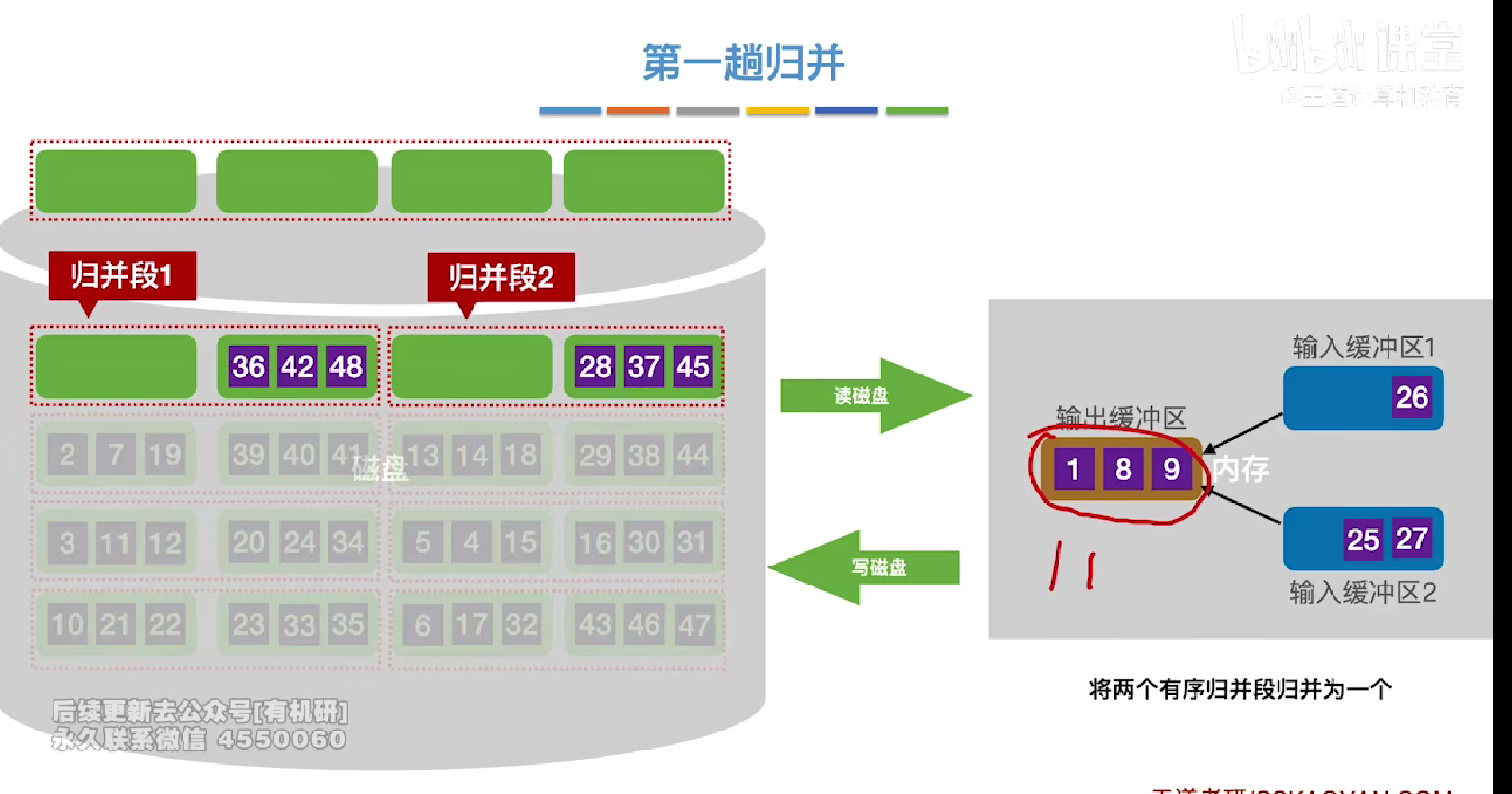
每次都挑选一个最小的块进行构造然后写入一个块放入外存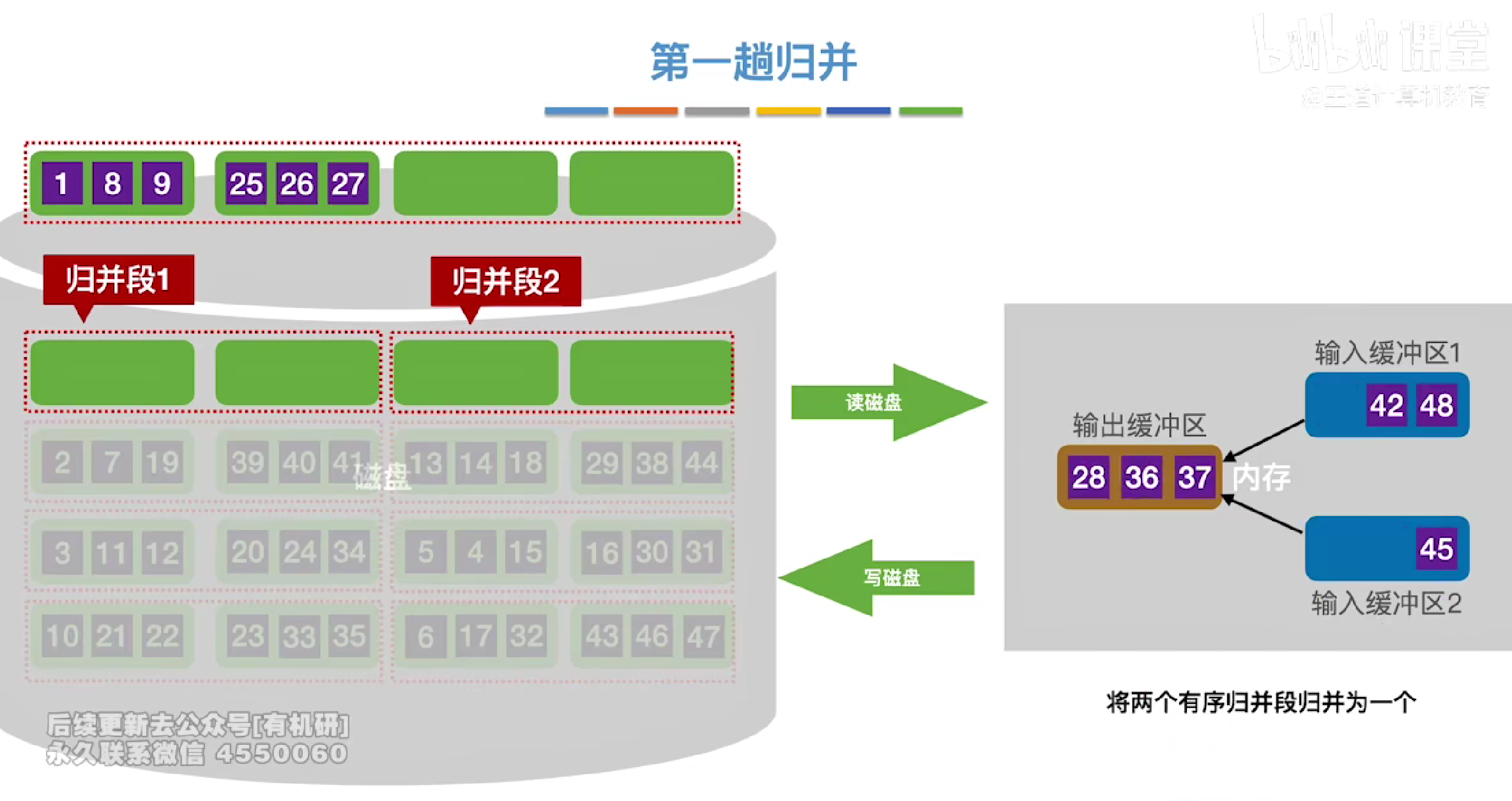
每当输入缓冲区空了就写入外存中
其中缓冲区1负责归并段1的块的读写
缓冲区2负责归并段2打的输入和读写
时间开销
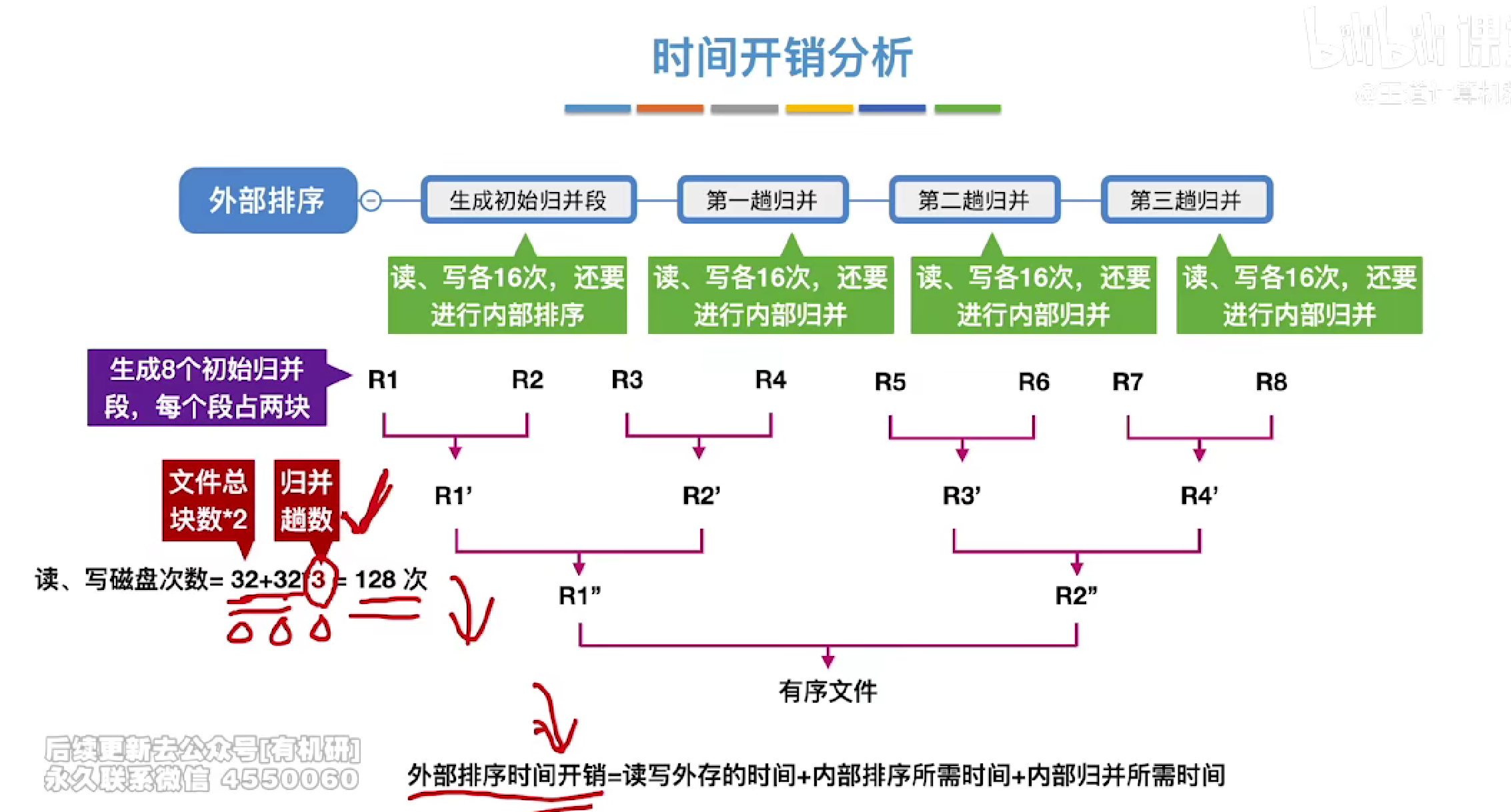
优化
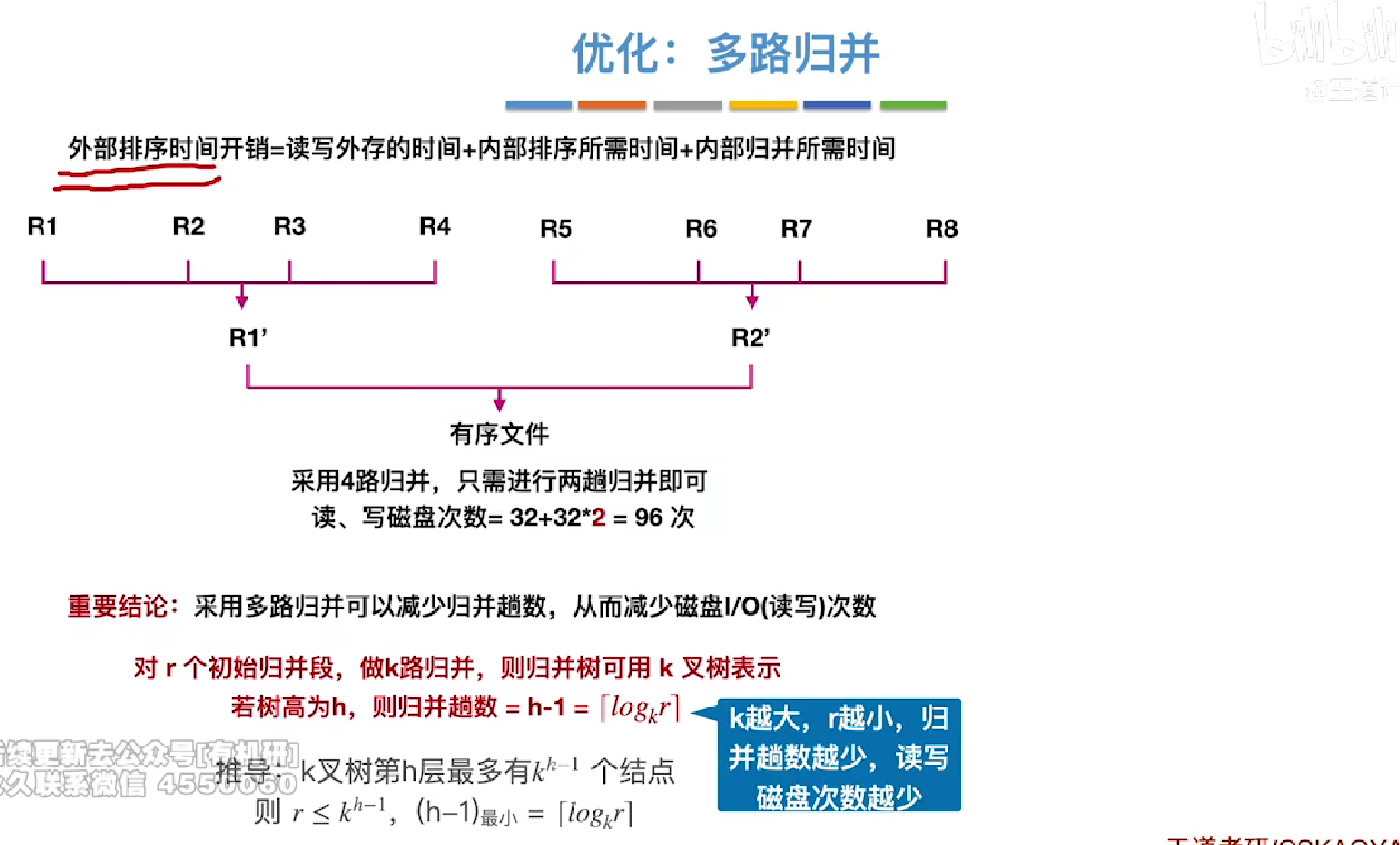


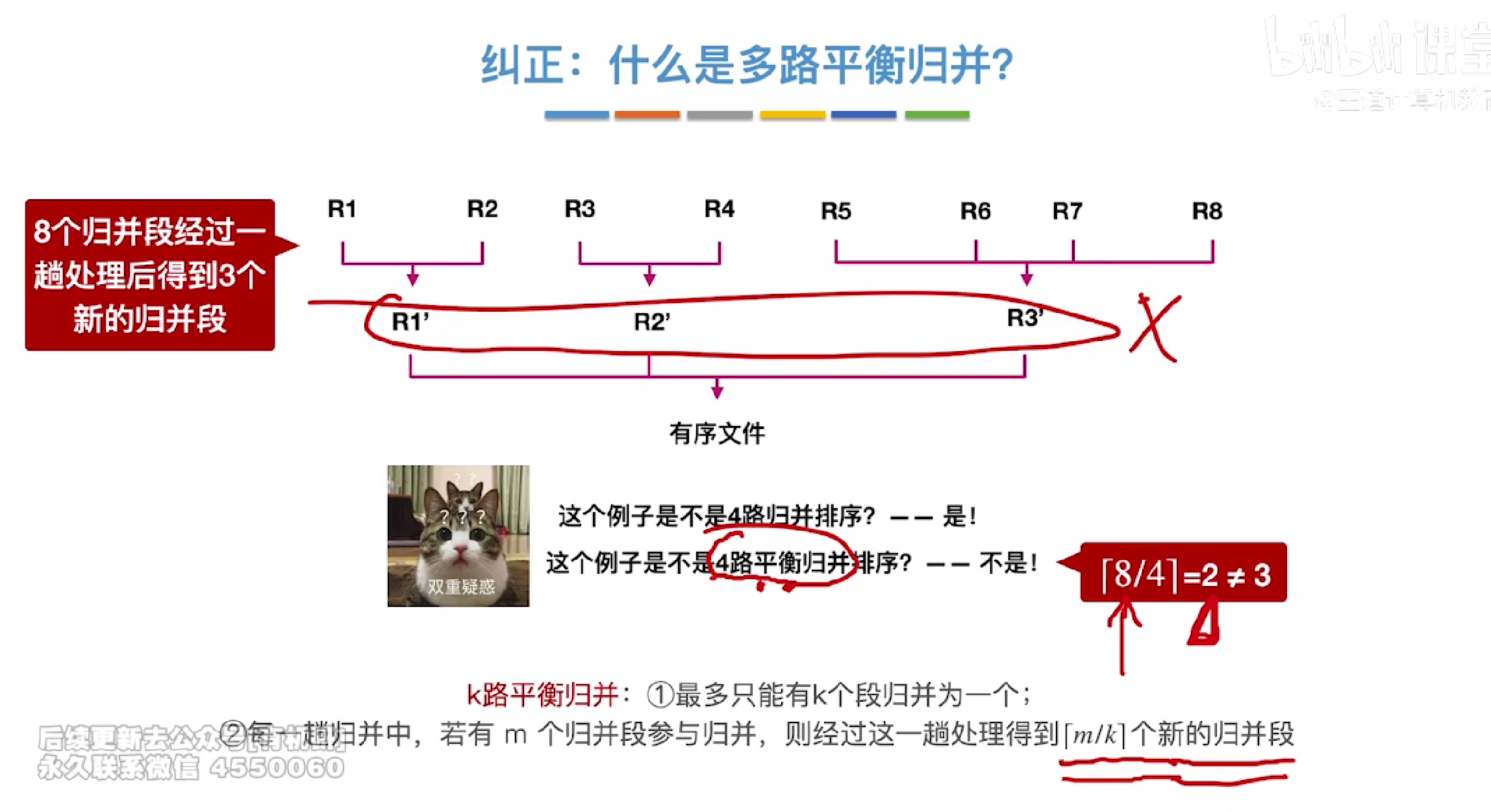
多路平衡归并
败者树

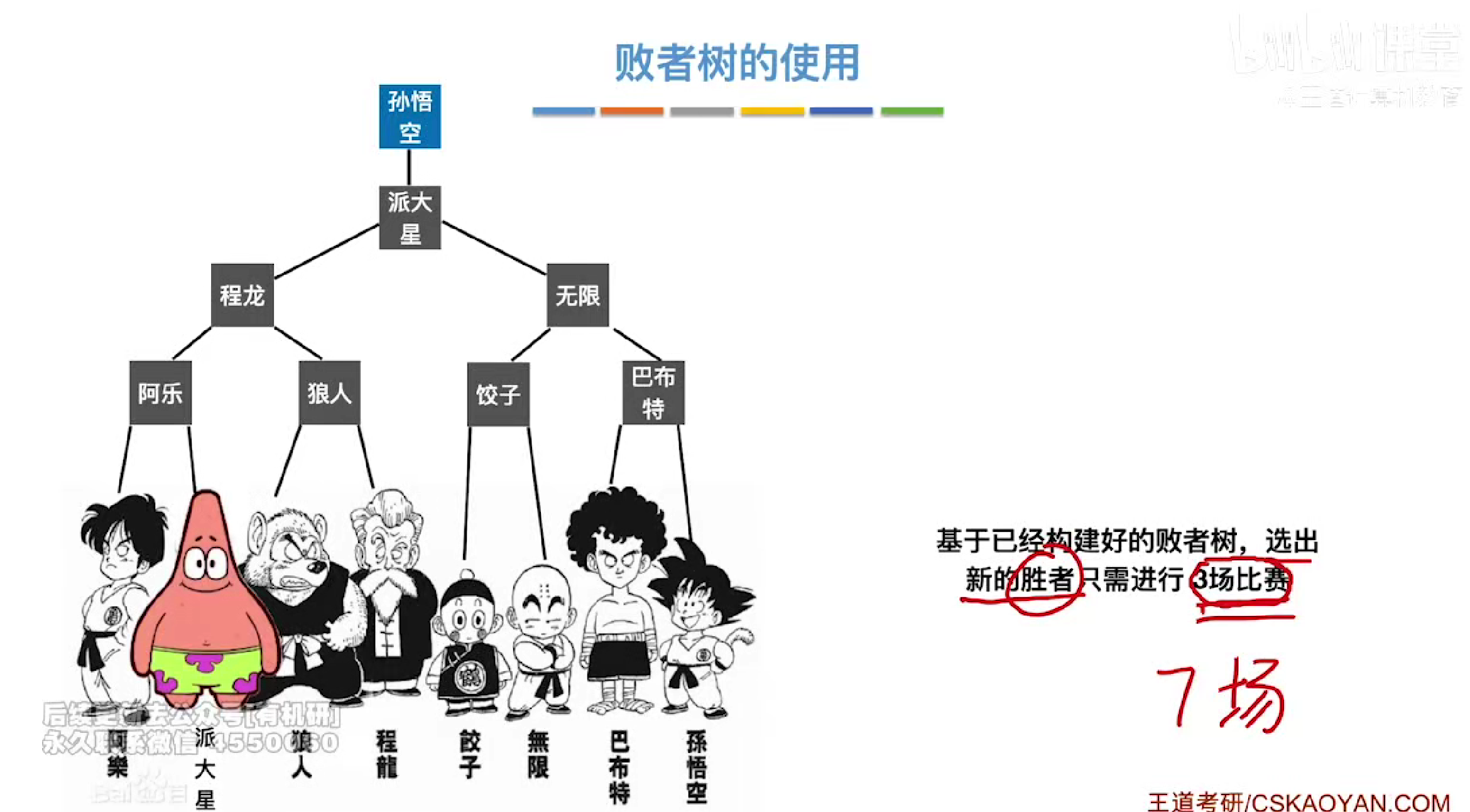
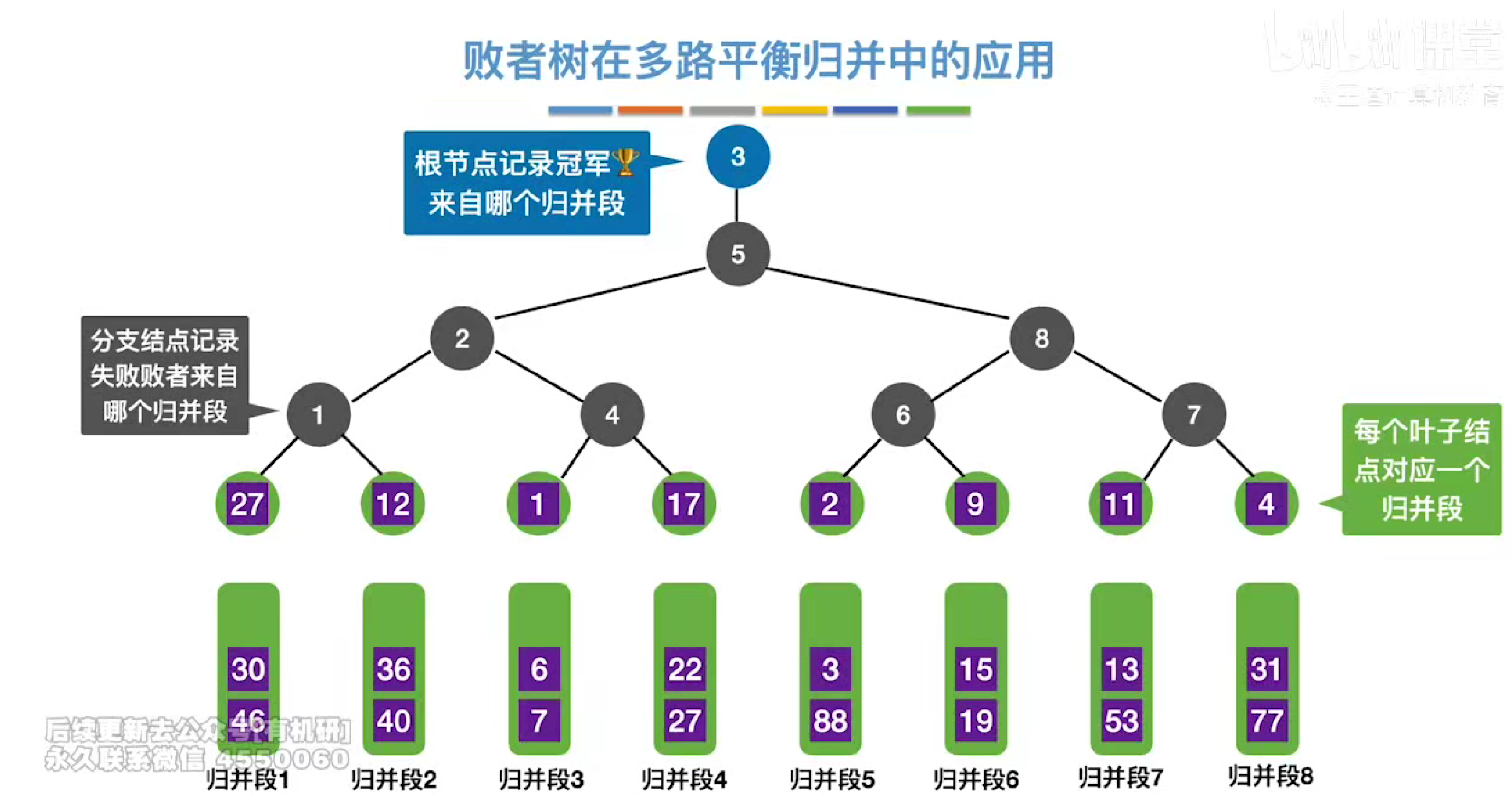
当我们第一次挑选了一个最小的元素之后,我们将原本1所在的位置,也即胜者诞生的归并断挑选下一个元素填入然后重新进行对比
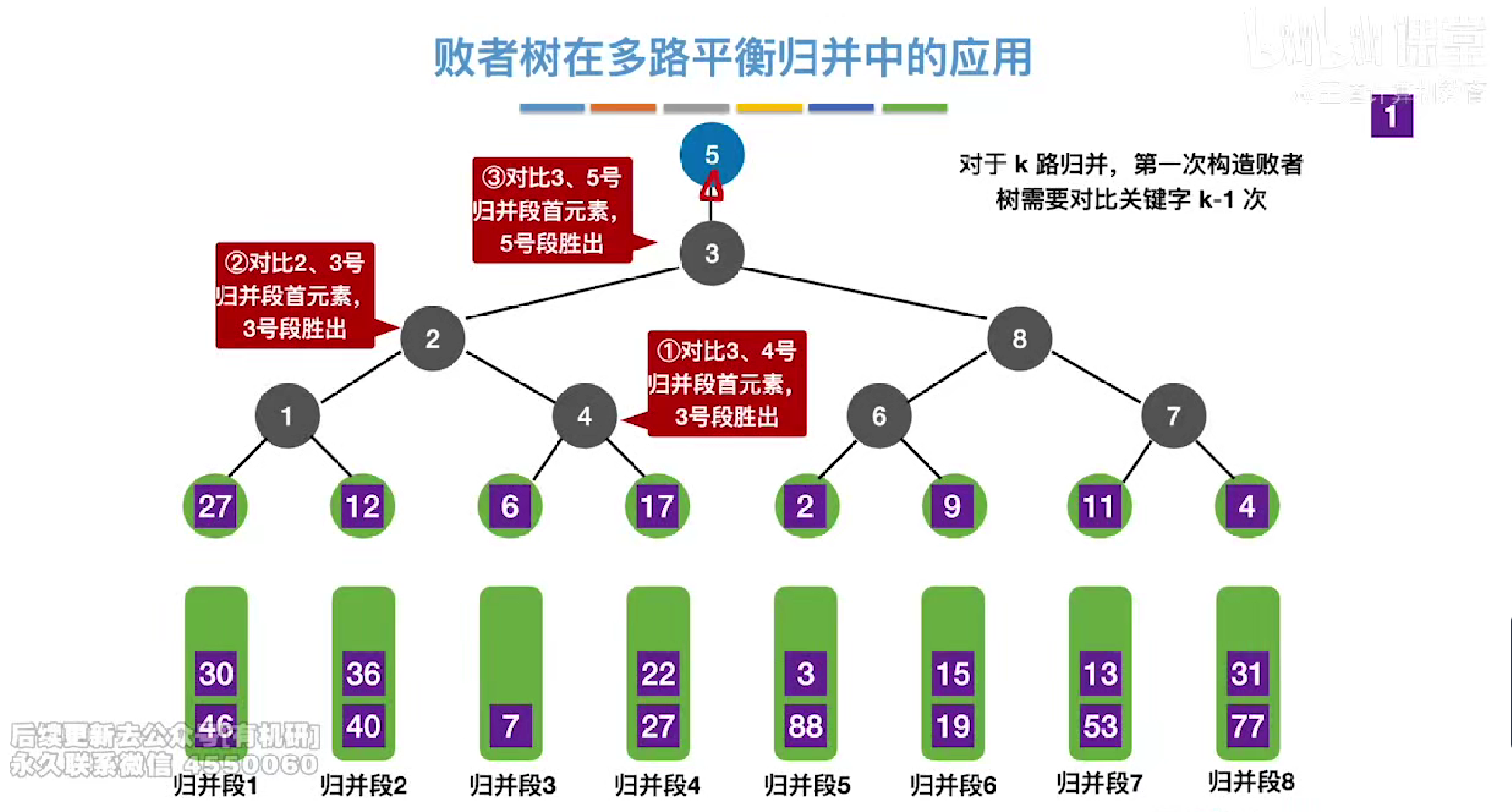
比较次数计算
对比次数=log2k向上取整
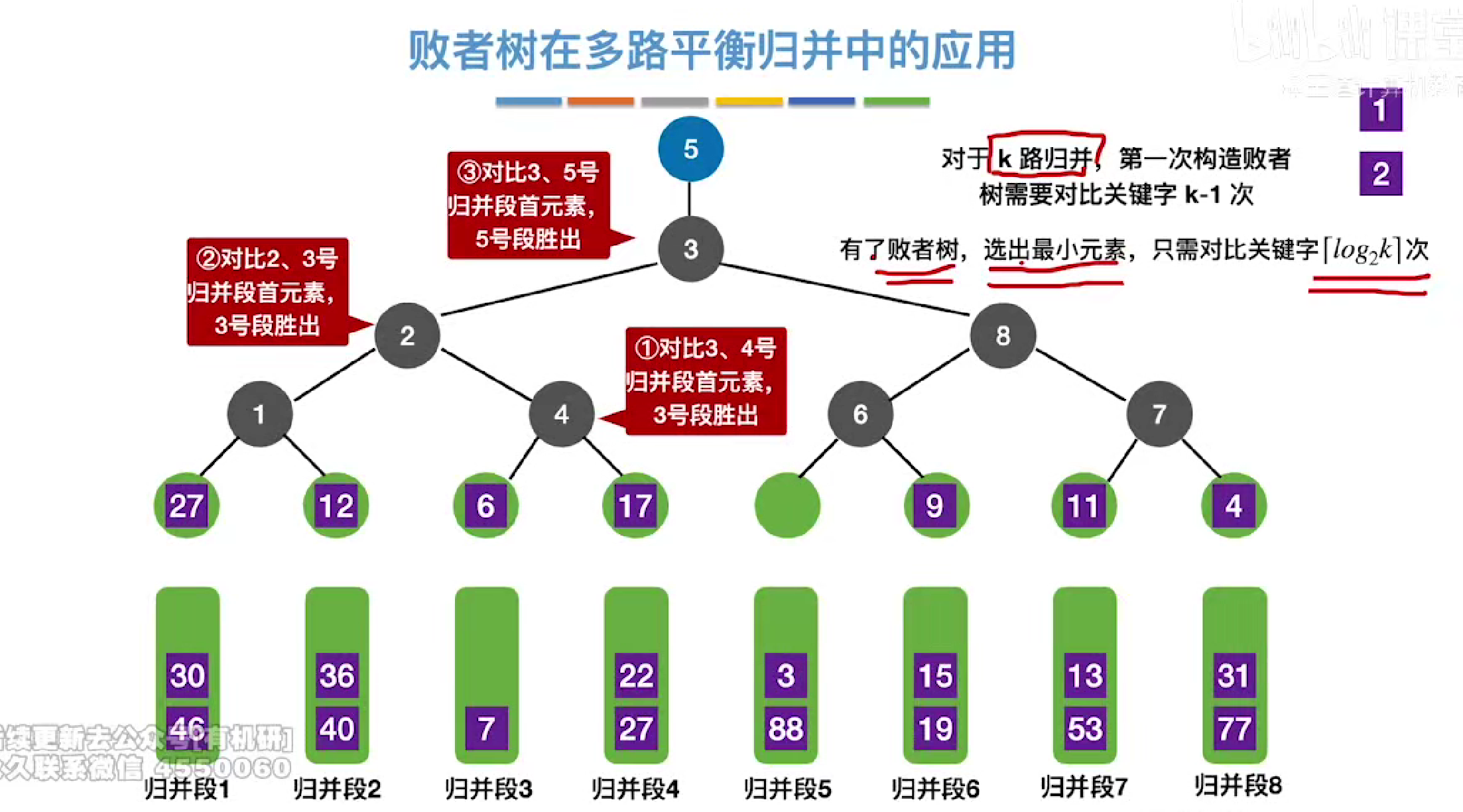
在k很大的情况下,那么败者树效率提升就会很明显
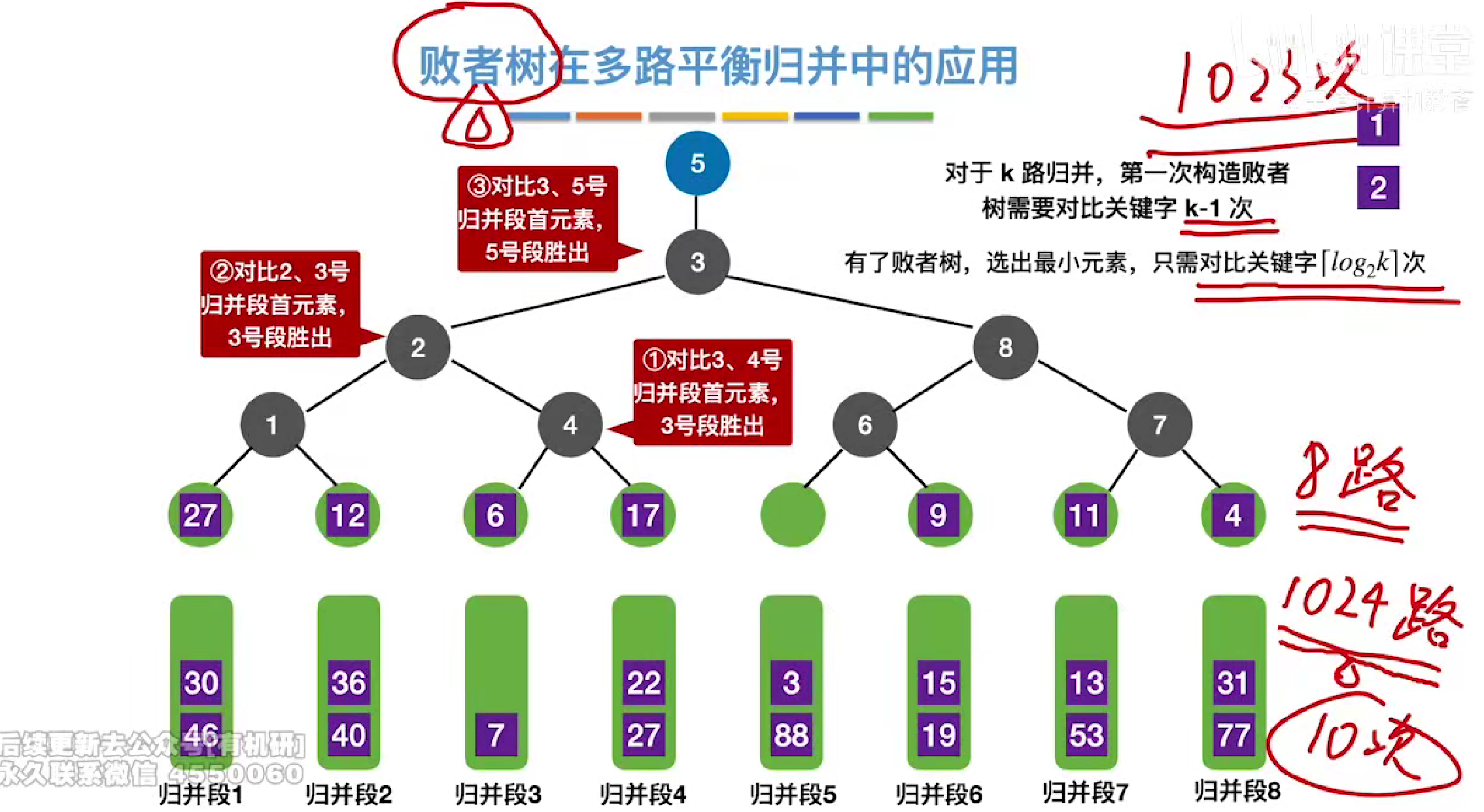

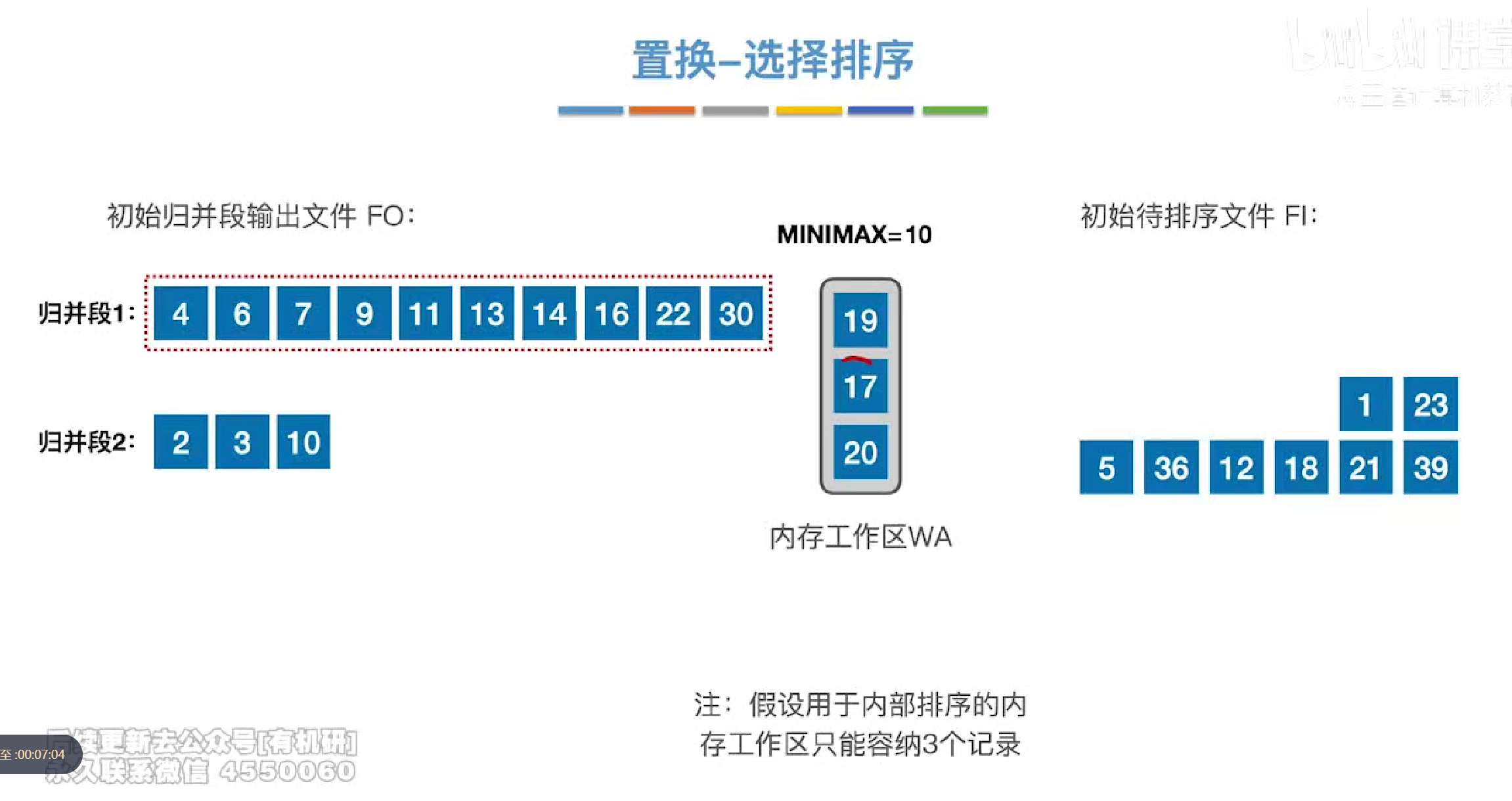
置换选择排序
构造归并段选用土办法每次只能选择缓冲区数量的记录然后进行内部排序构造一个整体有序的归并段
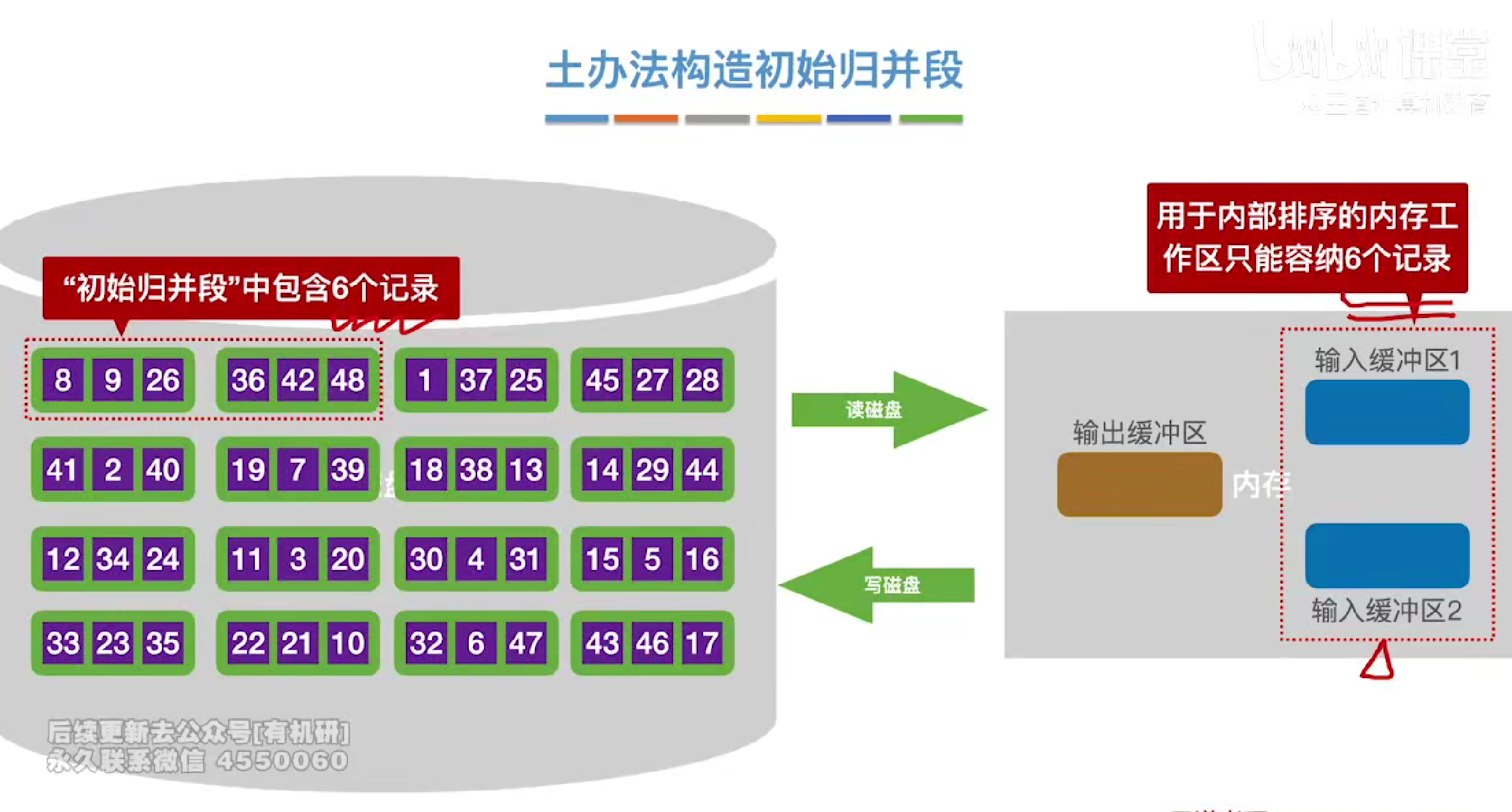

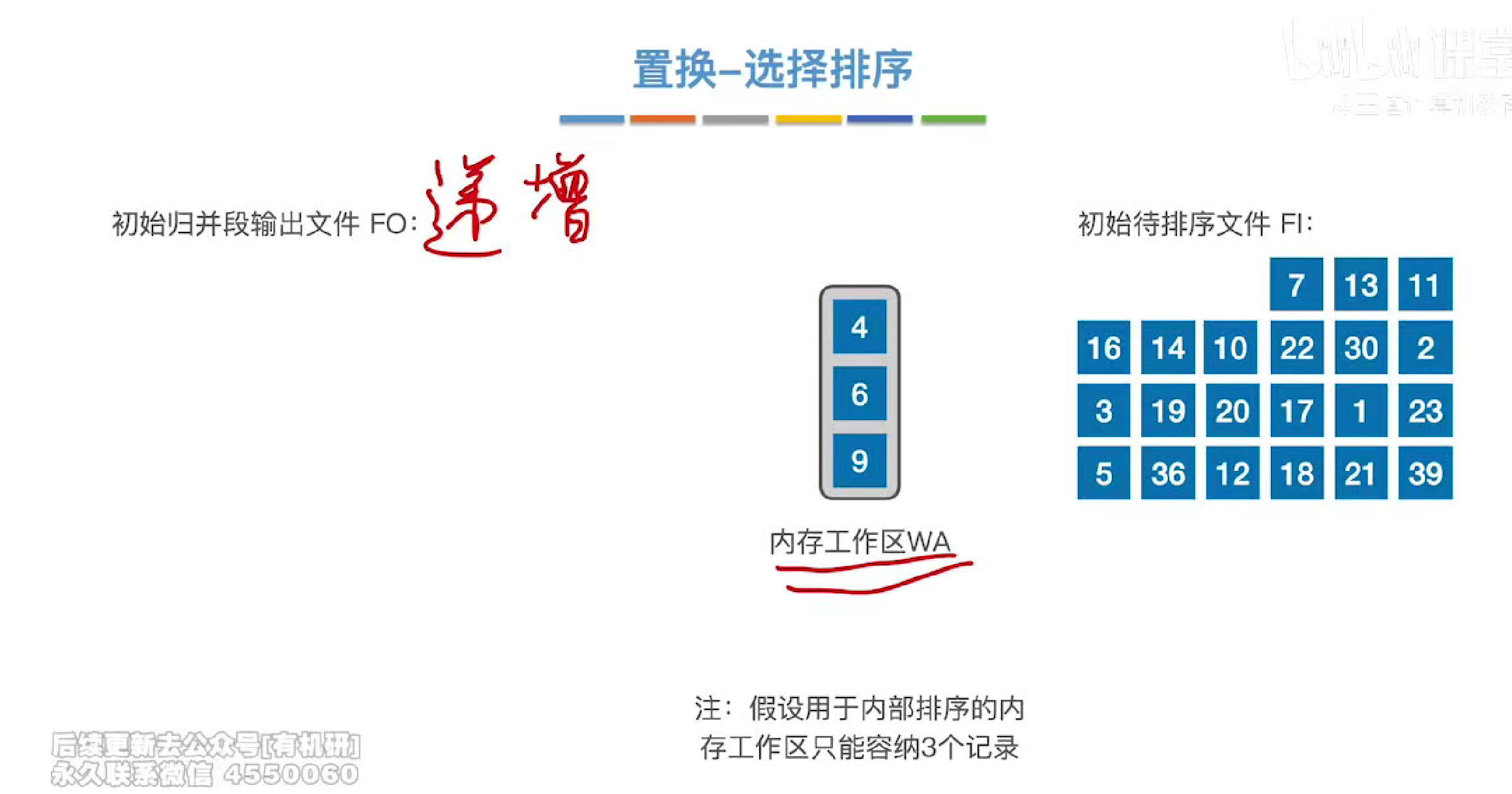
每次都会在wa中选择一个最小值放入输出文件fo中,如果后续的元素有小于目前归并段中的最大值的元素,就会在wa中保持不动。直到wa全部装满,然后再开启下一个归并段的构造
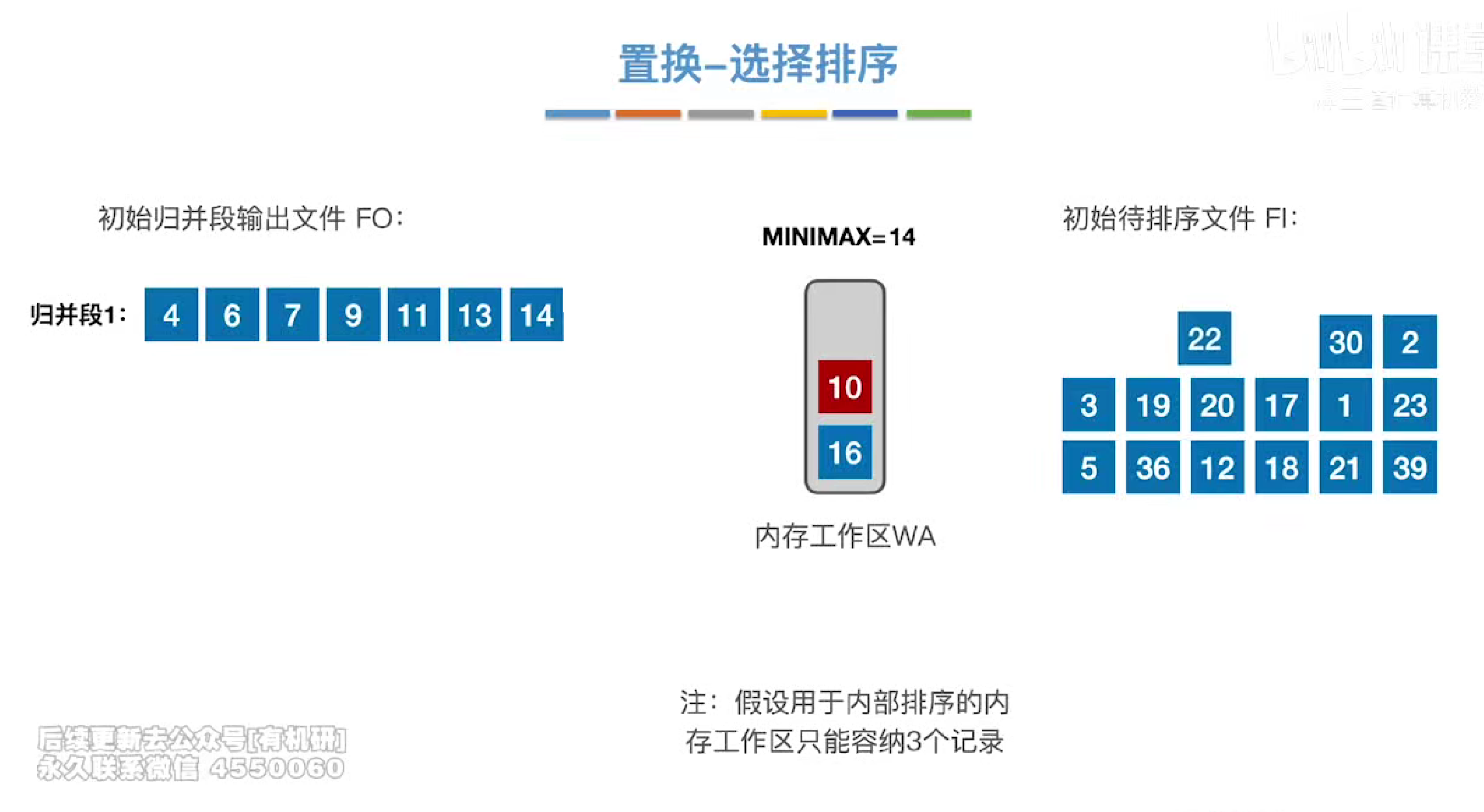
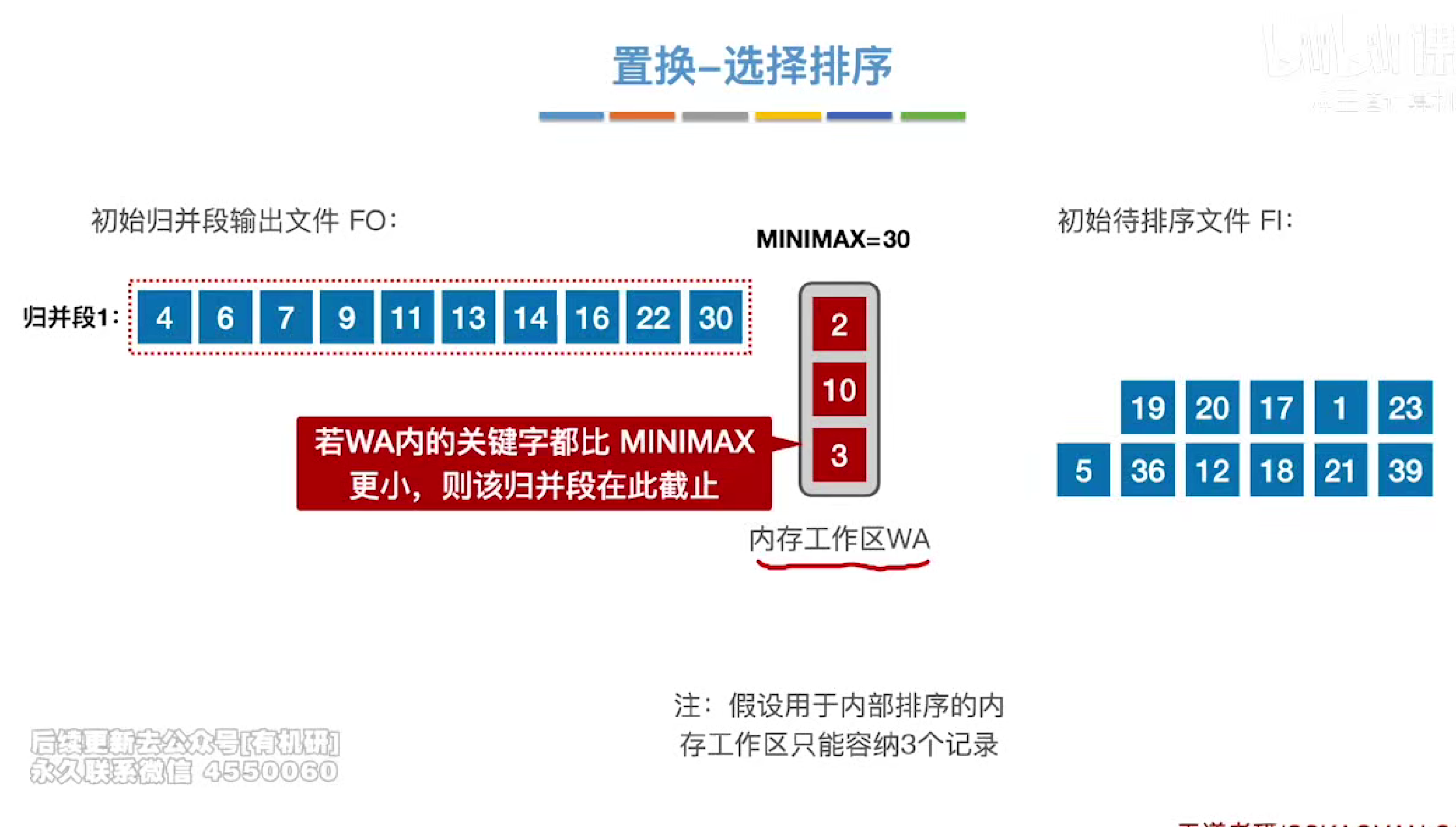
以此类推,可以用有限的内存工作区构造大于工作区长度的归并段
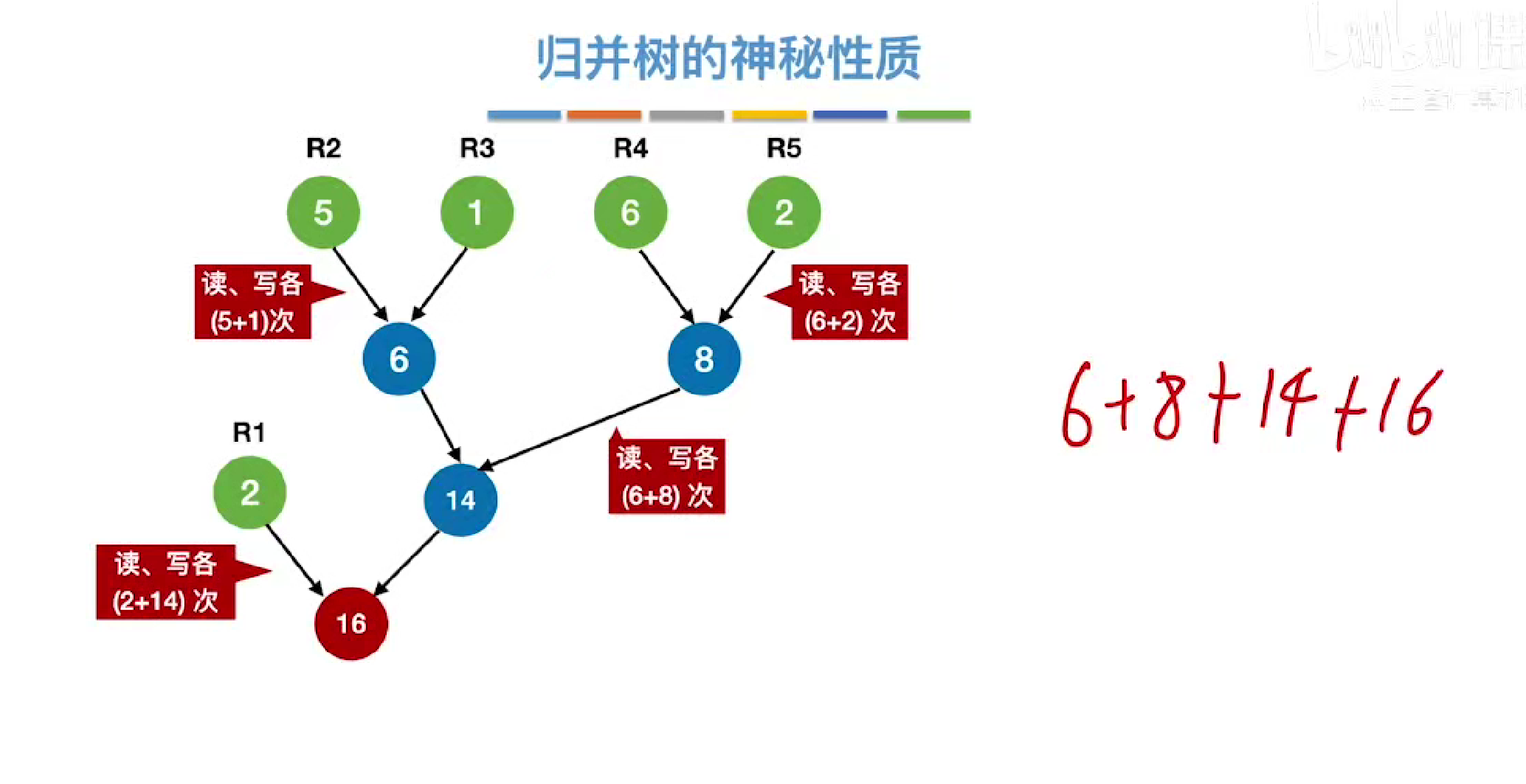
最佳归并树


用哈夫曼树构造最佳归并树
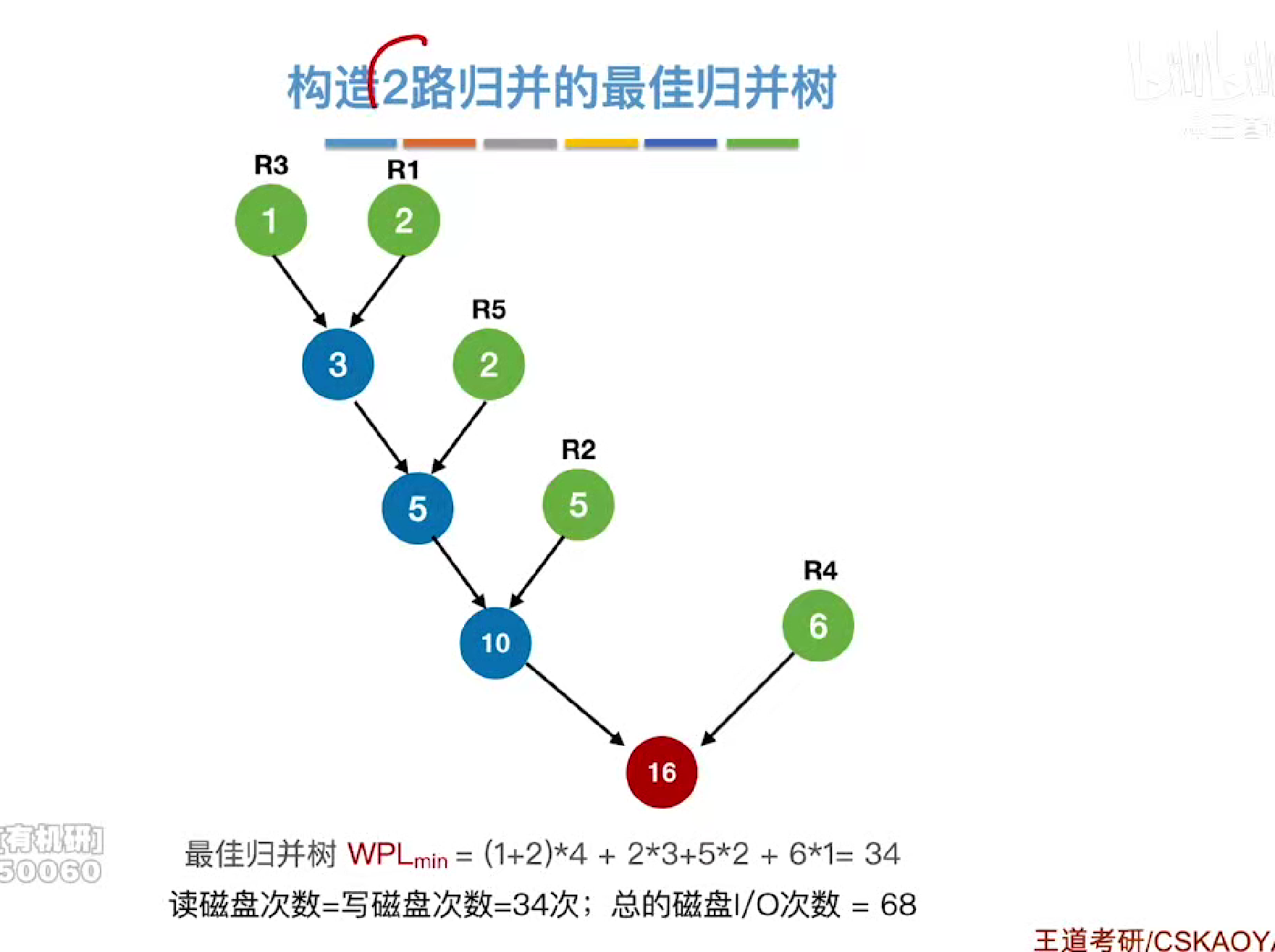
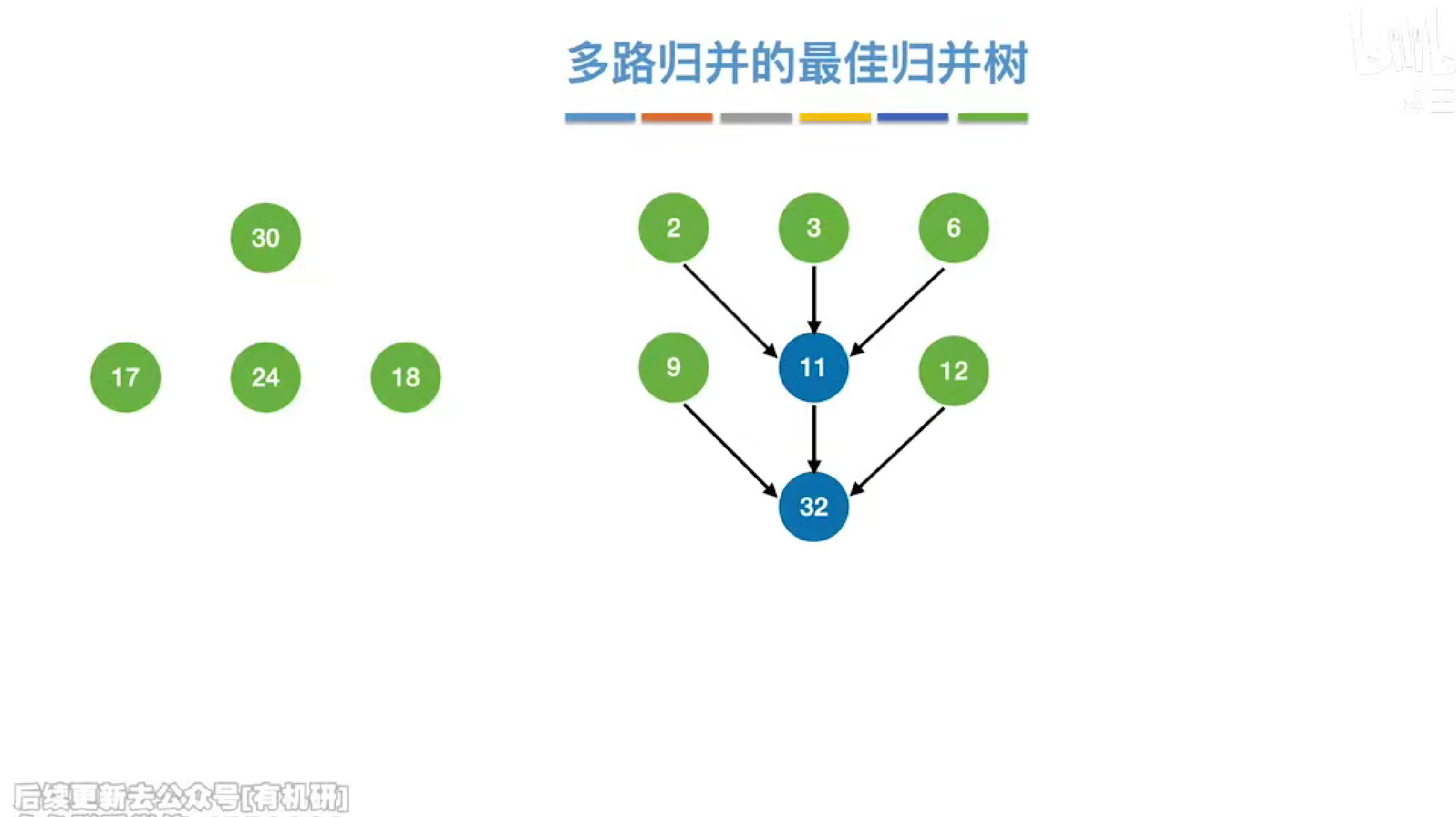
每次选择最小的几个进行归并
同哈夫曼树的构造一致
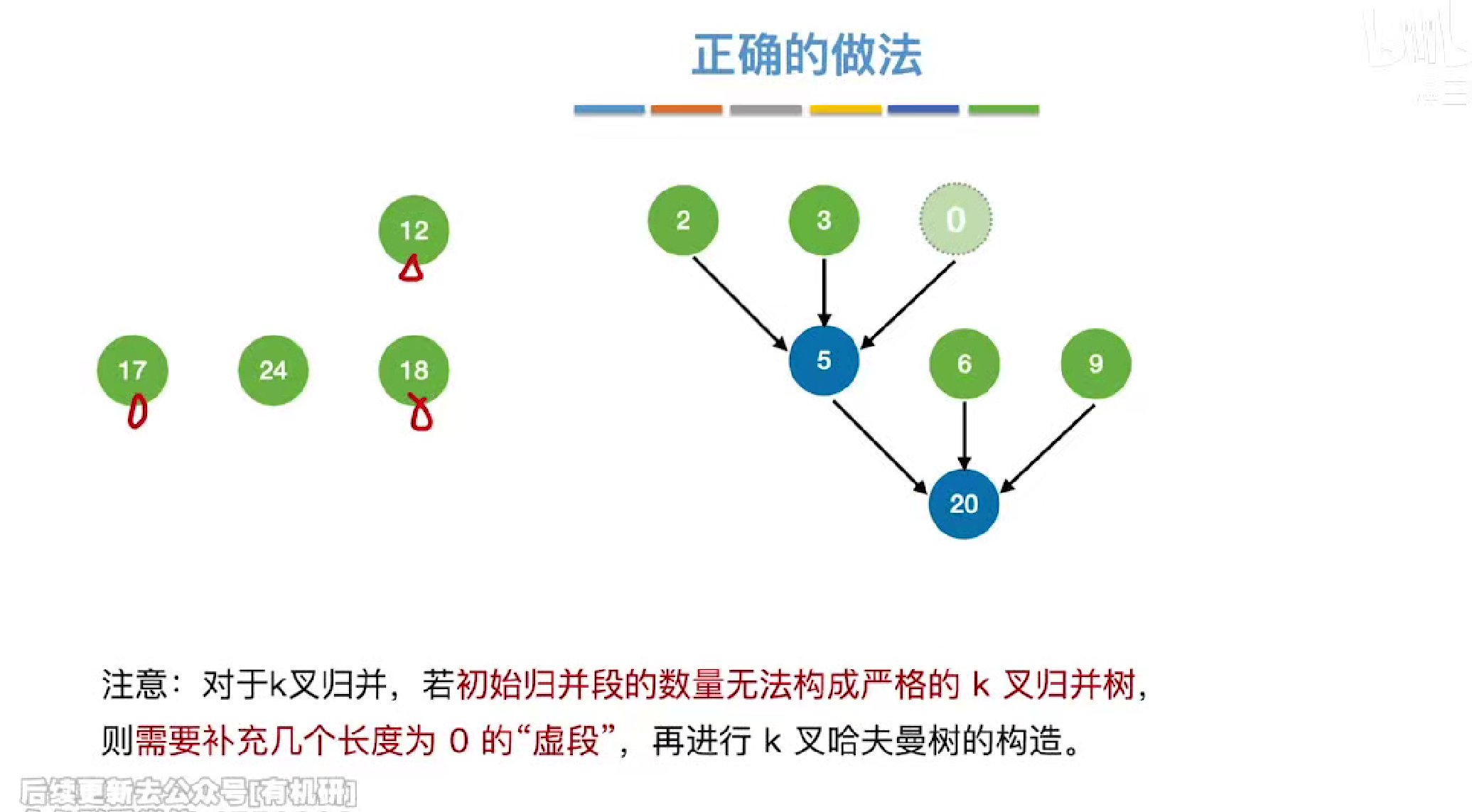
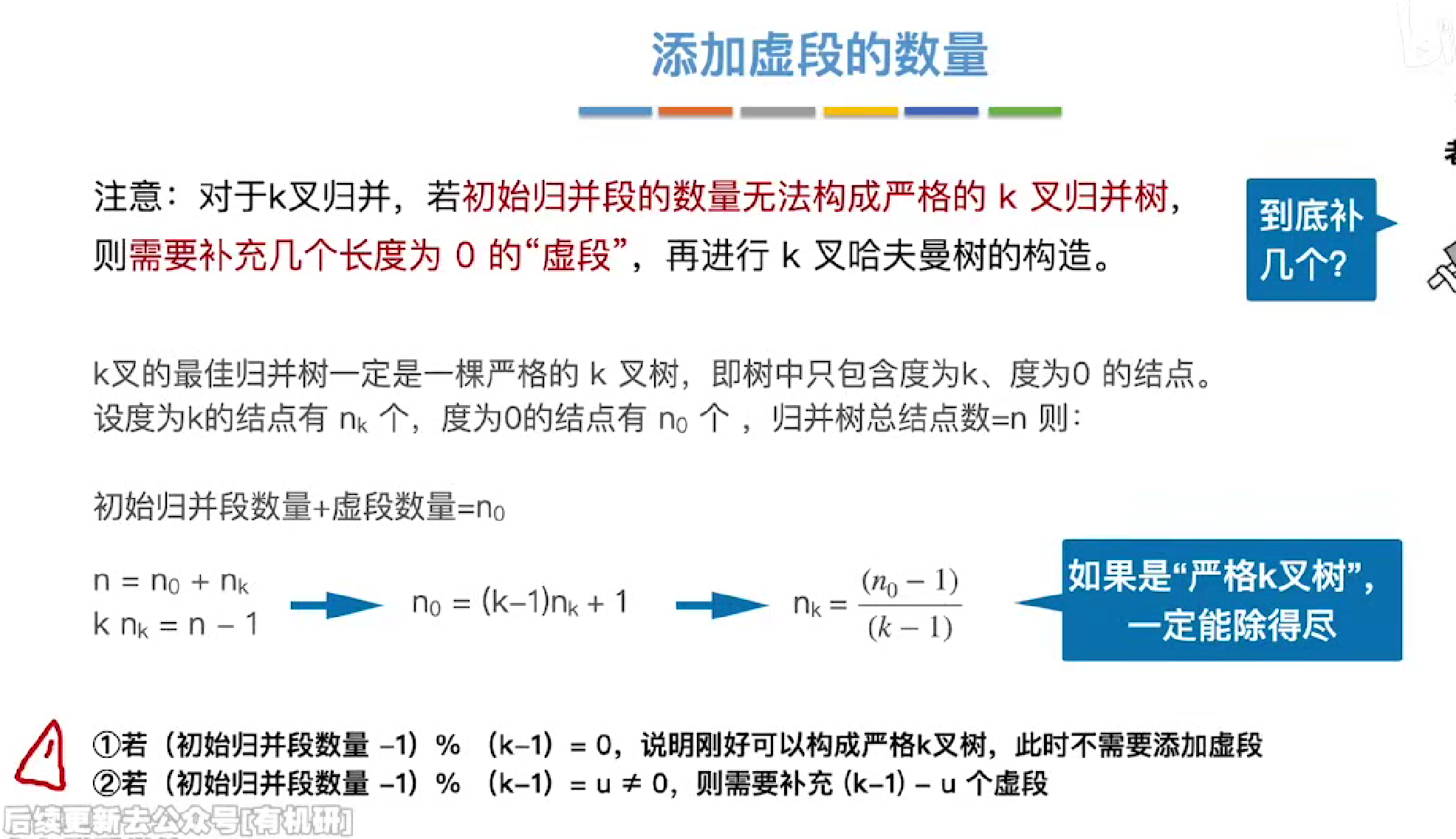
重点,节点数量和虚段数量间的关系
其中knk代表着k个度为n的结点,一个度对应着一个结点,所以全部加在一起就是knk
其中得到的数量就是所有节点除了根节点外的数量,所以要n-1
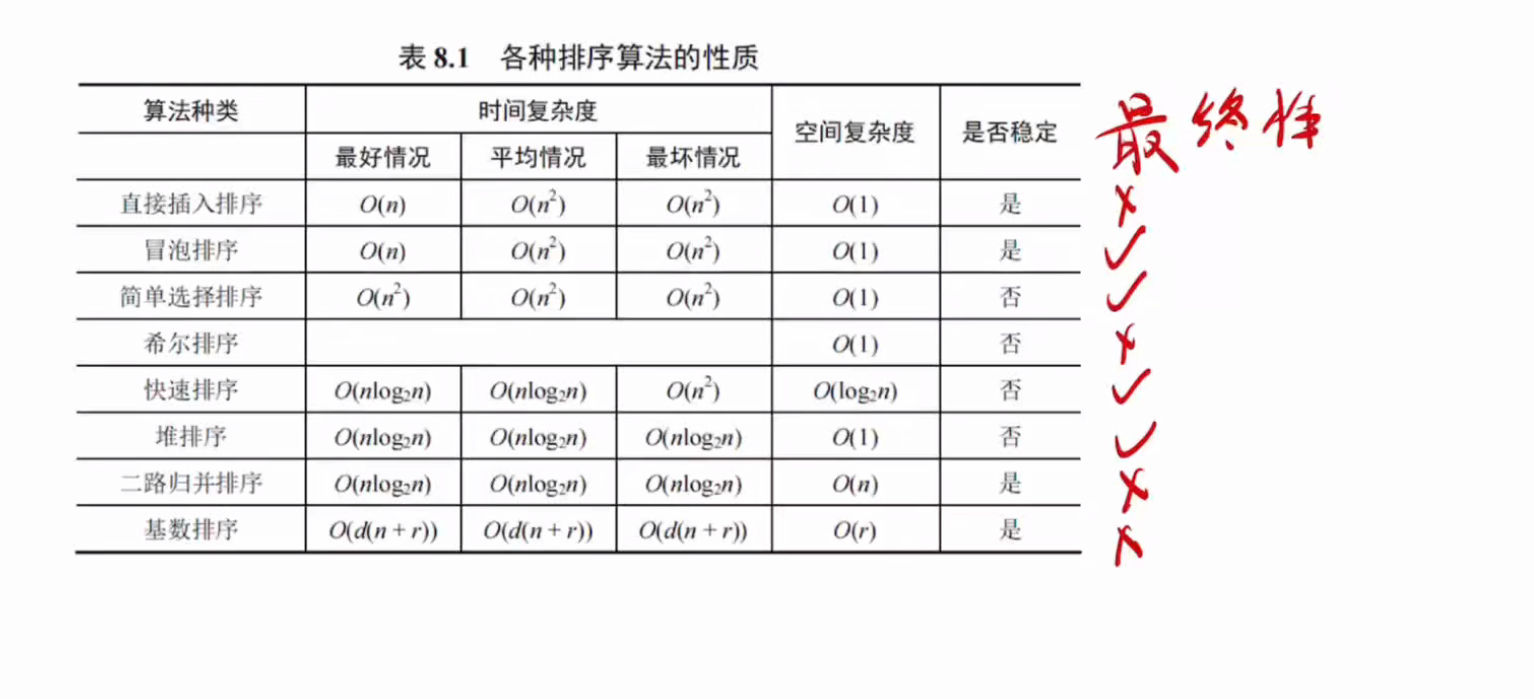
错题
重要考点
其中最终性指的是每一趟都能够选择一个放到最终的位置
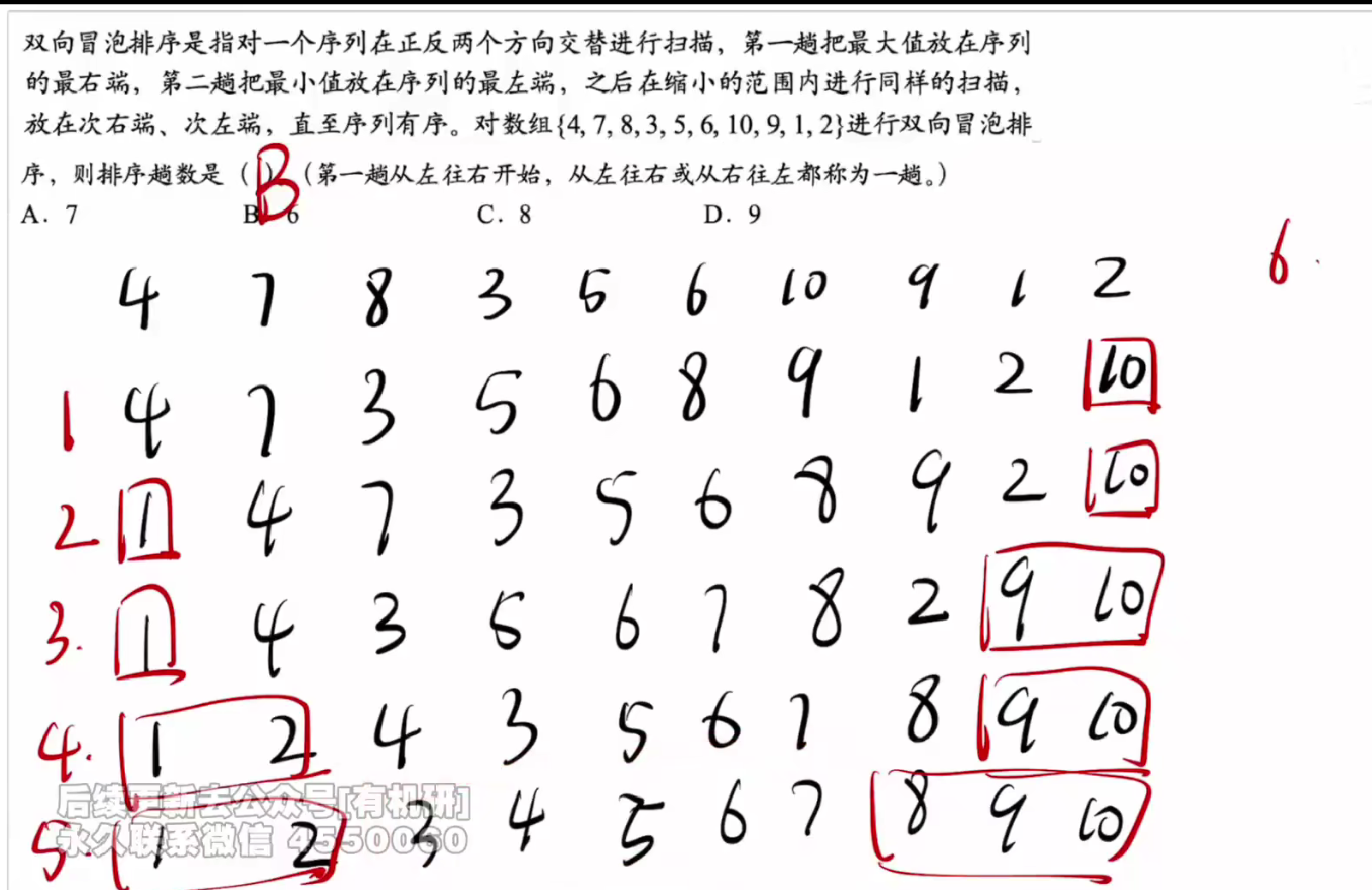
答案:B
书架元素整体有序,选择直接插入

答案:C
如图所示整体逆序情况就会出现题目所说的情况
而其他排序都至少能够保证一个元素回到其原本的位置

答案:A
希尔排序是直接插入排序,所以会有可能出现直接插入排序的情况

答案:B
冒泡排序需要有一趟无元素交换的检查趟数
如下图所示
最好情况是选取一个元素每次都能够平均的划分区间
那么有序的序列就可以达到效果
答案:D

答案:C
当删除和插入一个元素的时候
都需要堆堆进行调整,而调整的次数最坏的情况下也就是树高,即log2n的数量级

答案:A D
核心错误点在于建堆的过程中,其时间复杂度不会超过4n的复杂度
这一点要牢记

答案:A
其中快排主要是基准选择的怎么样,如果基准选择的好,那么比较次数就会少
冒泡排序,如果初始有序,一趟遍历过后发现没有交换则不会再进行比较

答案:B
如果进行孩子间的比较的话,右孩子是空的话那么就不会进行比较
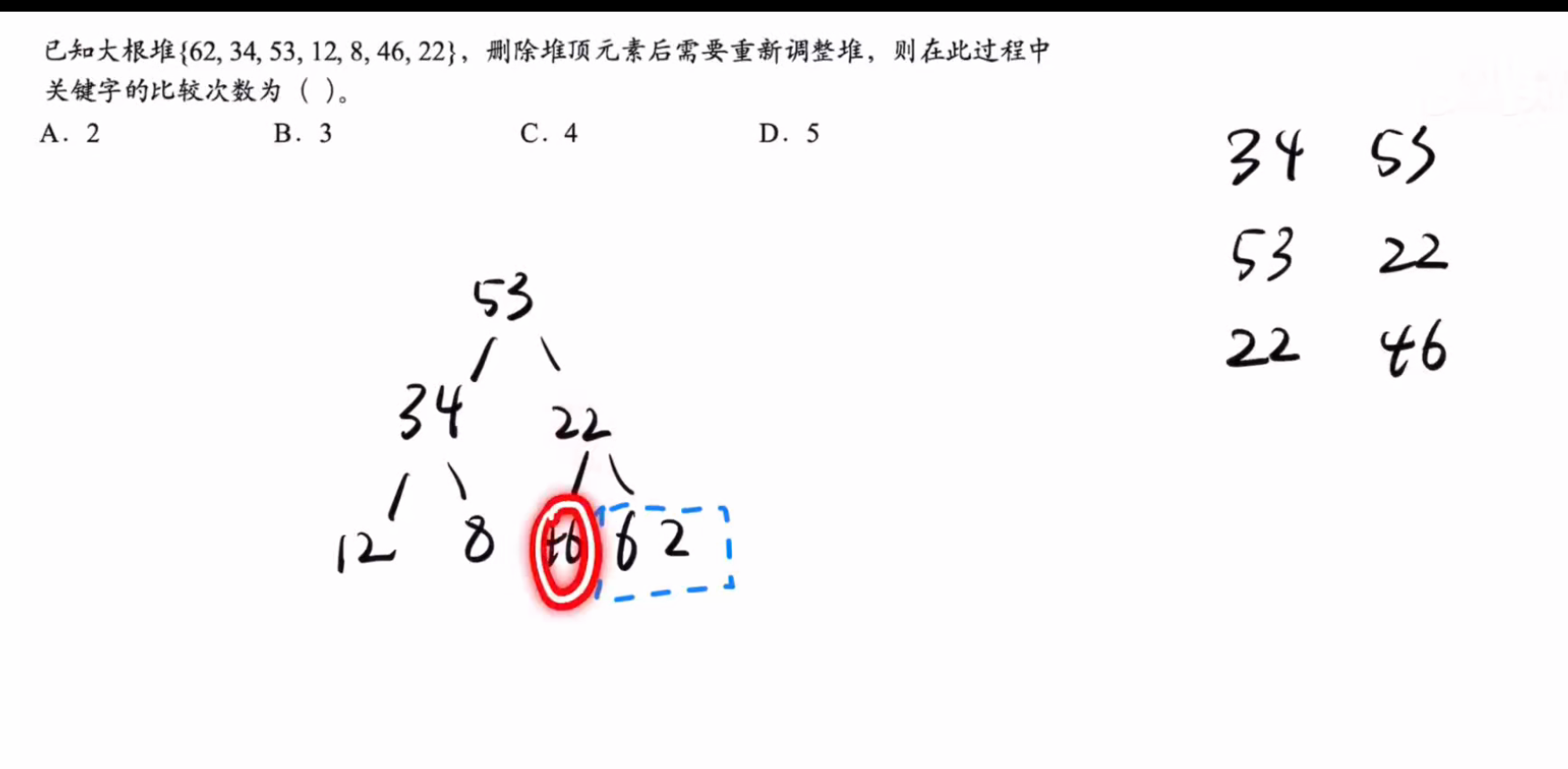
答案选择:B
公式为:n/k的m次方向上取整
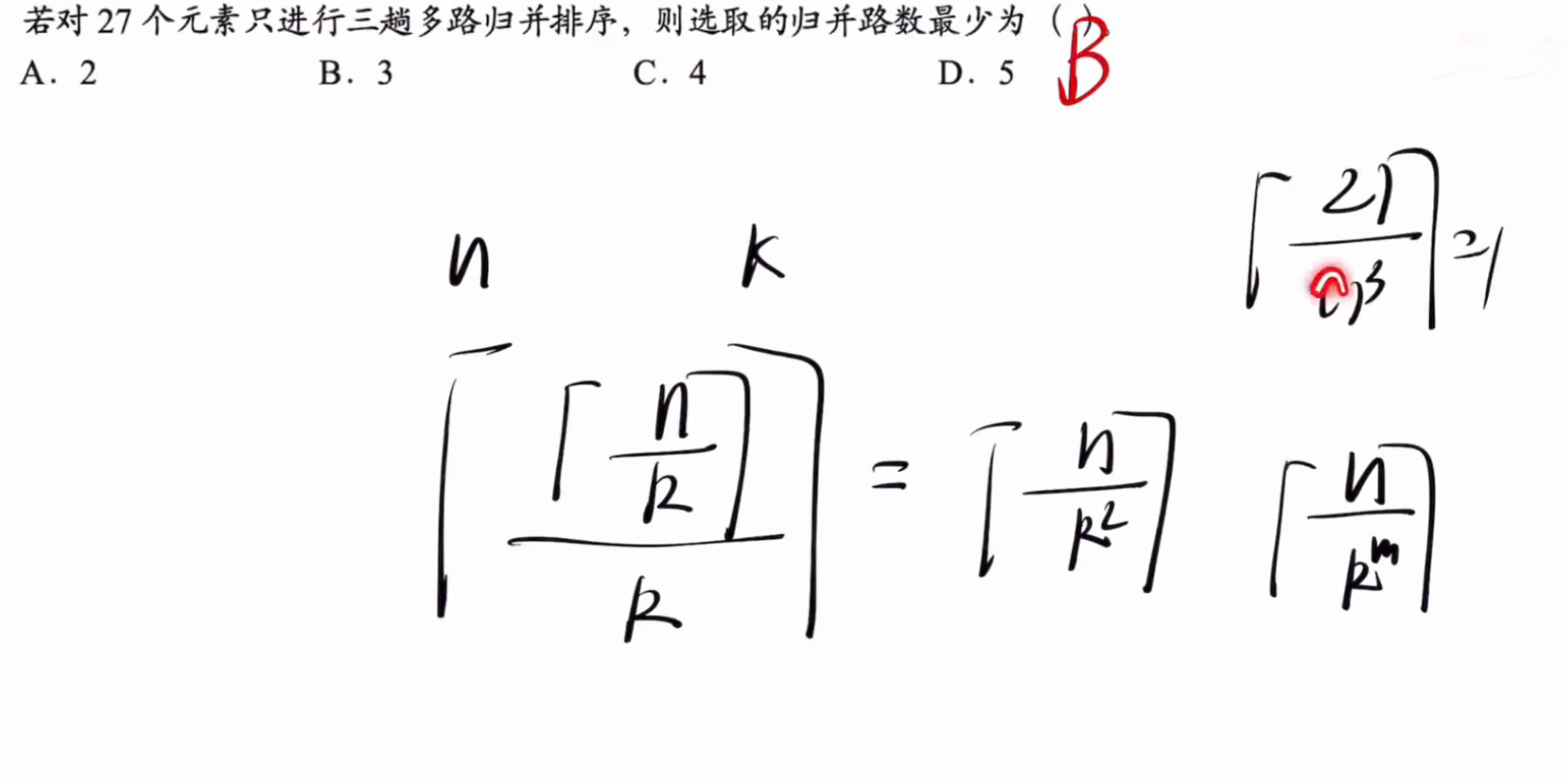
答案:D
对于这道题目,优先级次级的先排序,因为如果优先级高的成员变量先排序那么就会导致使用优先级低的成员变量排序时会改变原本的优先级高的顺序,即可能原本期望放到前面的数据被排列到了后面
而后还需要具有稳定性,对于高优先级成员变量排序的时候,如果不具有稳定性可能会破坏原本的次优先级成员变量排好的顺序

严格来说,时间复杂度最坏的情况下应该是m+n但是可以使用放缩的方法做出来本题
答案:D

答案选择:A
对于D选项,堆排序的比较次数还包括建立堆的比较次数
所以收到整体序列的影响
其中折半插入排序的判定次数基本相同,最差也就相差一
因为折半查找的前置条件就是序列基本有序,所以折半判定树一定是左右子树均匀或者相差1的
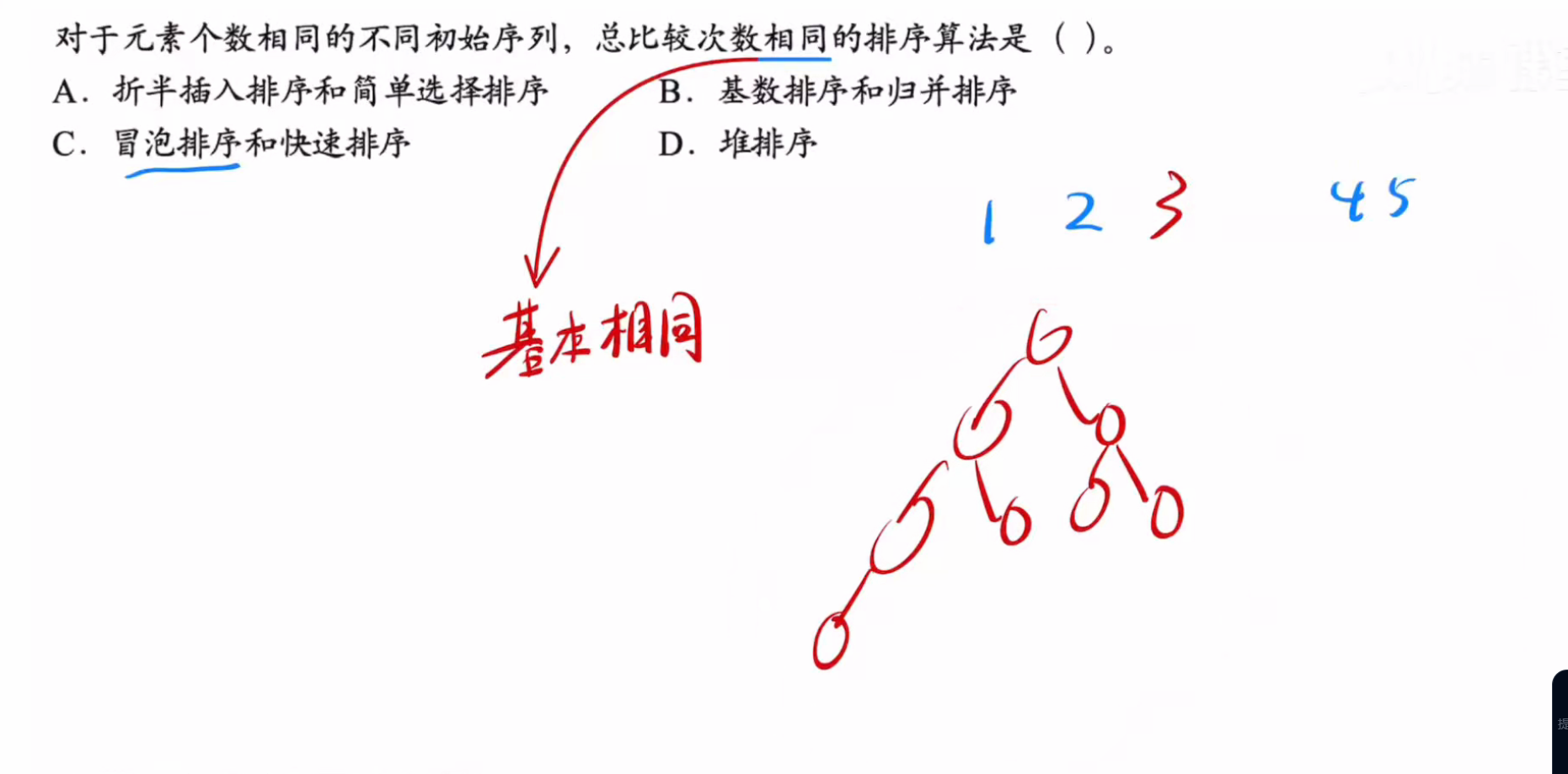
答案:C
对于堆这种数据结构,我们不能够按照树形结构进行查找,因为孩子元素的要求只是要求比根节点小,但是左右的方向没法区分,所以基本还是遍历查找存储他的数组

答案:B
内存中600个记录排好序后构成一个初始归并段
375000/600=625
所以归并段数目为625
五路归并中需要进行5轮次归并即可归并完毕625个归并段
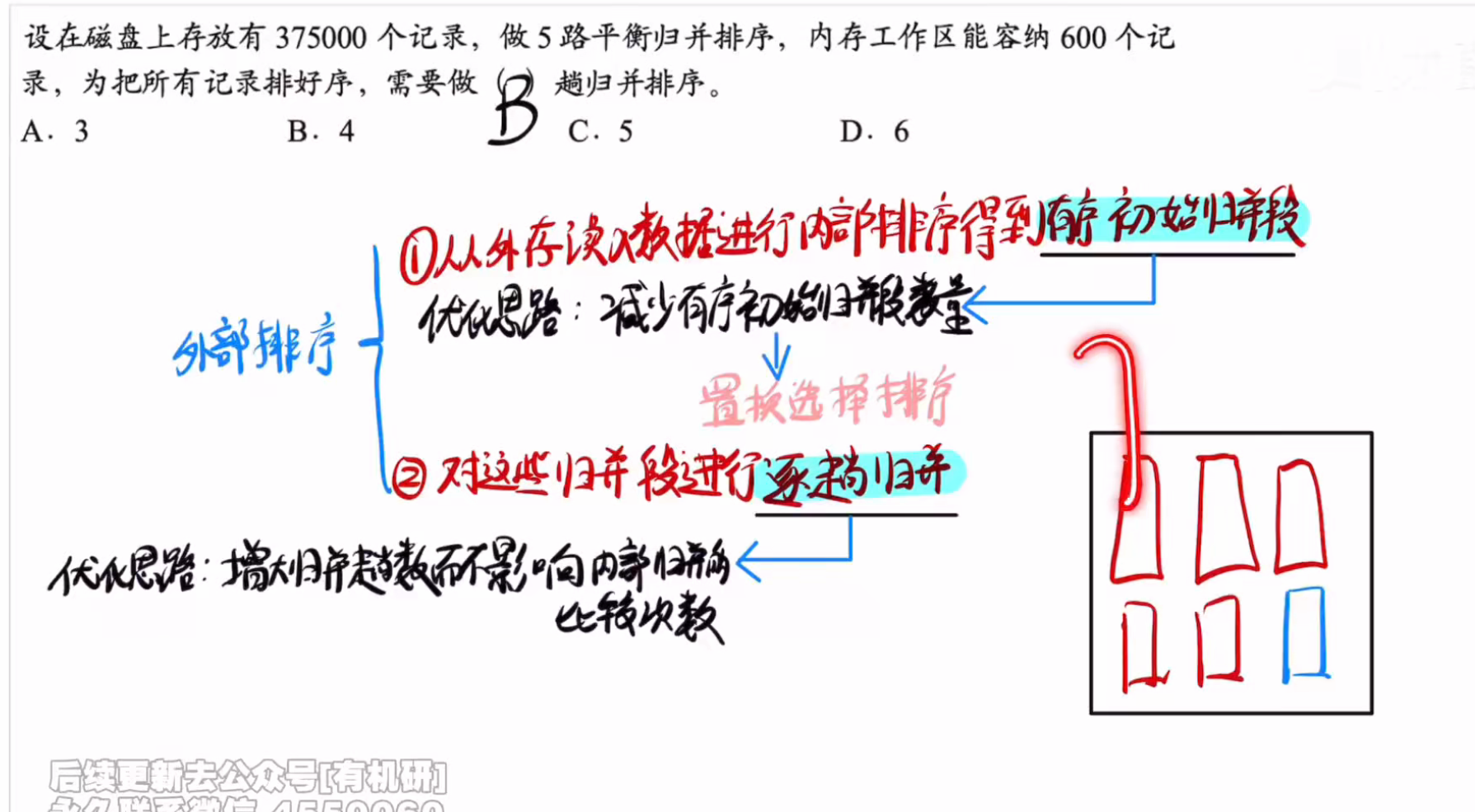
答案:D
输入记录来自于外存输入进来的,需要存放在内存中进行操作的
输出记录是需要将内部排好序的记录输出到外存中去的
输出缓冲区:就是输出记录存放的地方,用于接受内存排好序的输出,比如划分归并段,当输出缓冲区满的时候则输出到外存中去