当前位置：首页 > news >正文

非参数密度函数估计(1)

news 2025/7/26 9:09:38

一、说明

非参数密度估计是一种估计随机变量概率密度函数的方法，无需假设分布的特定函数形式与需要选择特定分布（如正态分布或指数分布）的参数方法不同，非参数方法直接从数据中估计密度，这使得它们更灵活但可能更复杂。

二、基本原理

设 $X_1，...，X_n$ 是从分布P中抽取的样本，其密度为p。非参数密度估计的目标是在尽可能少地假设p的情况下估计p。我们用 $p^\hat{p}$ 表示估计量。估计量通常依赖于调节参数h，谨慎选择h至关重要。为了强调对h的依赖性，有时我们写作 $p^h\hat{p}_h$ 。一个非常简单的非参数分布估计量就是经验分布:
$Pn=1n∑i=1nδXiP_n = \frac{1}{n} \sum_{i=1}^{n}δ_{X_i}$
（关于经验分布参看：https://yamagota.blog.csdn.net/article/details/148089446?spm=1001.2014.3001.5502）

但经验分布并不适合用来估计底层分布。它通过将所有概率质量集中在给定的训练点 {Xi} 上，对训练数据“过拟合”，甚至在非常接近的点上也没有任何质量。此外，它也没有密度。
因此，通常在非参数密度估计中，我们指的是做一些更多的事情，特别是通过“平滑”经验分布 $Pn\mathbb{P}_n$ 。出于这个原因，非参数密度估计也经常被称为平滑。
$∑ggl=1n\sum gg{l=1}{n}$
$∏i=1n∑i=1n\prod_{i=1}^n {\displaystyle \sum _{i=1}^{n}}$
图1的左上图显示了密度

$\frac{1}{2} φ(x; 0, 1) + \frac{1}{10} \sum _{i=0}^{4} φ(x; (j/2) -1;1/10)$

其中φ(x; μ, σ)表示均值为μ，标准差为σ的正态密度。Marron和Wand（1992）称这种密度为爪形，但我们称之为巴特·辛普森密度(Bart Simpson density)。

基于从p中抽取的1000个样本，我们计算了一个核密度估计器，将在后面描述。该估计器依赖于一个称为带宽的调节参数。右上图基于一个小带宽h，导致欠平滑。右下图基于一个大带宽h，导致过平滑。左下图基于一个选择以最小化估计风险的带宽h，这导致了一个更合理的密度估计。
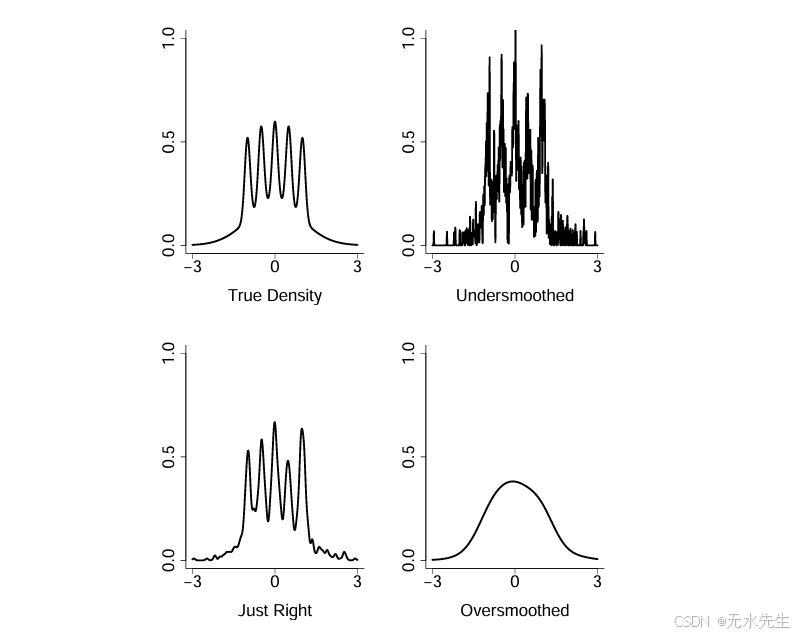
在这里插入图片描述
图1：来自示例1的巴特·辛普森密度。左上：真实密度。其他图表是基于n=1000次抽样的核估计。左下：通过交叉验证选择的带宽h=0.05。右上：带宽h=10。右下：带宽10h。

二、非参数密度估计应用

密度估计可用于采样新点（参见此类采样在图像和文本领域涌现的创意应用，这些应用甚至可能令人担忧），更广泛地说，它为下游概率推理提供了数据的紧凑摘要。它还可以特别用于回归、分类和聚类。假设p(xy)是对p(xy)的估计。

回归: 然后我们可以计算以下回归函数的估计值：
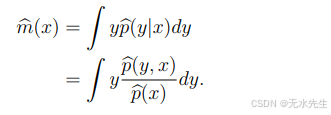
分类: 在进行分类时，回忆贝叶斯最优分类器。

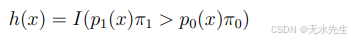
其中π1 = P(Y = 1)，π0 = P(Y = 0)，p1(x) = p(x|y = 1) 和 p0(x) = p(x|y = 0)。将π1和π0的样本估计值以及p1和p0的概率密度估计值代入，可以得到贝叶斯分类器的估计值。许多你熟悉的分类器都可以用这种方式重新表达。
聚类。在进行聚类时，我们寻找高密度区域，基于密度的估计。在讨论聚类时，我们将进一步探讨这一点。
异常值检测。密度估计有时也用于寻找不寻常的观测值或离群点。这些是pb(Xi)非常小的观测值。
两样本假设检验。密度估计可用于两样本测试。给定 $X_1，...，X_n∼p$ 和 $Y_1，...，Y_m∼q$ ，我们可以使用 $D(p^，q^)D(\hat{p}，\hat{q})$ 来测试 $H 0 ： p = q$ ，其中D是一个发散度量作为检验统计量。

3 损失函数（Loss Functions）

最常用的损失函数是L2损失
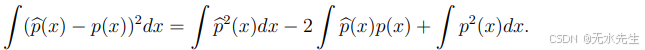
在这里插入图片描述
其风险在于：

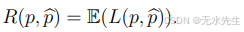
L2损失的一个关键优势是风险具有非常数学上方便的分解：

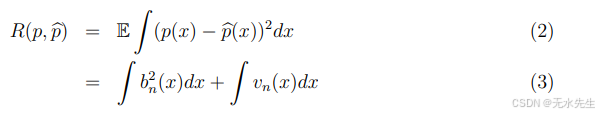
偏执项

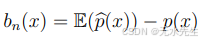
方差项

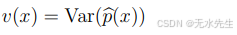
估计器pb通常涉及以某种方式“平滑”经验分布。主要挑战在于确定要进行多少平滑处理。当数据过度平滑时，偏差项较大而方差较小。当数据不足平滑时，情况则相反。这被称为偏差-方差权衡。最小化风险对应于平衡偏差和方差。
德沃耶和吉尔菲（1985年）强烈主张使用L1范数
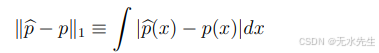
在这里插入图片描述
将损失替换为L2。L1损失具有以下良好的解释。如果P和Q是定义总变差度量的分布

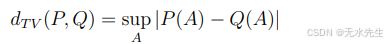
其中上确界是针对所有可测集而言的。现在如果P和Q有密度p和q，那么

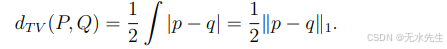
因此，如果 |p−q| < δ，那么我们知道对于所有A，|P(A)−Q(A)| < δ/2。此外，L1范数是变换不变的。假设T是一个一一光滑函数。设Y = T(X)。设p和q为X的概率密度函数，令pe和qe为Y对应的概率密度函数。
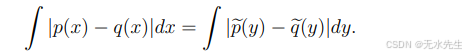
在这里插入图片描述
因此，距离不受变换的影响。在某种意义上，L1损失比L2损失更适合密度估计。但它更难处理。目前，我们将专注于L2损失。但以后我们可能会讨论L1损失。

另一种损失函数是Kullback-Leibler损失 $\int p (x) l o g (p (x) / q (x)) d x$ 。这并不是一个适合用于非参数密度估计的良好损失函数。原因是Kullback-Leibler损失完全被密度比的尾部所主导。
在一类密度函数P上的最小最大风险是
在这里插入图片描述
并且，如果一个估计器的风险等于最小最大风险，则称其为最小最大估计器。我们说pb是速率最优的如果

通常，最小最大速率的形式为 $n^{(-C/(C+d))}$ ，其中 C > 0。