2024年ASOC SCI2区TOP，基于强化学习教与学优化算法RLPS-TLBO+风电场布局优化，深度解析+性能实测

---

1.摘要

随着全球对可再生能源需求的增长，风能作为一种环保能源得到了广泛关注。风力发电被视为减少碳排放、推动可持续发展的重要手段之一。在风电场中，多个风力发电机组协同工作，但下游风机不可避免地受到上游风机尾流的影响，导致部分风能未能得到有效利用。为减少尾流影响、提高风电场的发电效率并降低成本，本文提出了一种基于强化学习教与学优化算法（RLPS-TLBO），该算法的主要创新包括：将串行改为并行，加速收敛并提高效率；引入强化学习调整参数F，用于优化更新阶段的选择；在改进学习者阶段，新增个体参与更新，并提出选择概率以增强算法保留优质个体信息的能力。

2.风电场布局优化问题

尾流建模

风电场中尾流损失的预测是一项具有挑战性的工作，因为其本质涉及诸多复杂的非线性因素。风作用于风机叶片并驱动其转动的速度，会受到风速、湍流强度、叶片气动特性、桨距角等气象和控制参数的共同影响。经过一系列非线性损耗后，每台风机都以不同的最优状态发电，而风流经过风机后速度会降低，并形成带有湍流的尾流。叶片的旋转还会引入进一步的湍流，其强度与初始风速、湍流强度、叶片转速及偏航角等密切相关。最终，这些尾流在空间中横向和纵向扩散，表现出高度不确定性，因此准确的尾流建模对于评估风电场发电损失至关重要。

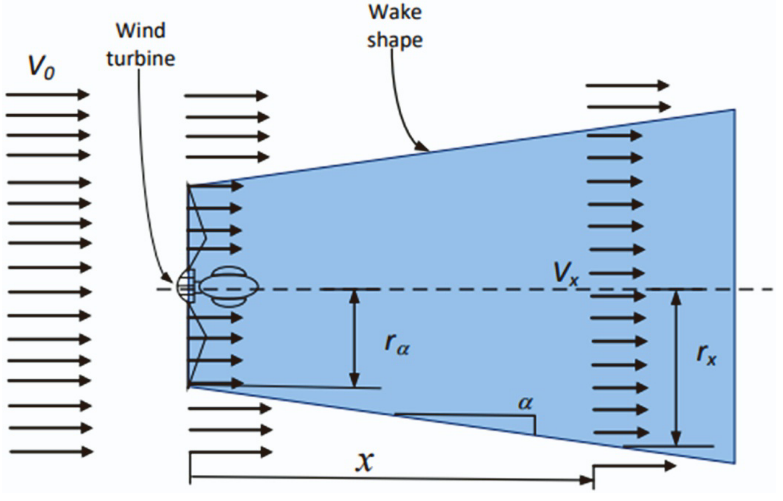
目前，常用的尾流模型有Jensen模型、Larsen模型、Frandsen模型等。其中，Jensen尾流模型以其简明的结构和较高的预测精度，成为应用最广泛的解析模型。图中展示在恒定风速下Jensen单尾流模型，根据动能守恒定律，可以计算距离风机一定距离处的尾流风速：
$$V_x=V_0-a\left(\frac{r_{\alpha }^2}{r_x^2}\right)\times V_0$$

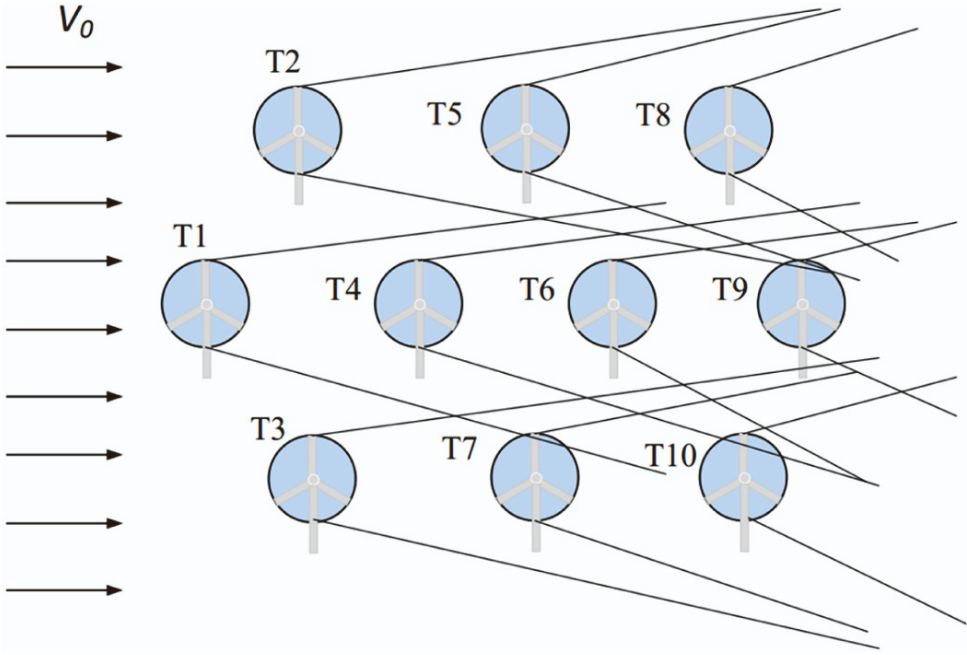
在实际风电场中，多个相邻涡轮尾流的联合效应会导致更显著的尾流影响。根据动能守恒原理，当涡轮受到多个尾流的影响时尾流速度：
$${\nu }_{xi}={\nu }_o\left[1-\sqrt{\sum _{i=1}^{N_t}{\left(1-\frac{{\nu }_{xi}}{{\nu }_o}\right)}^2}\right]$$

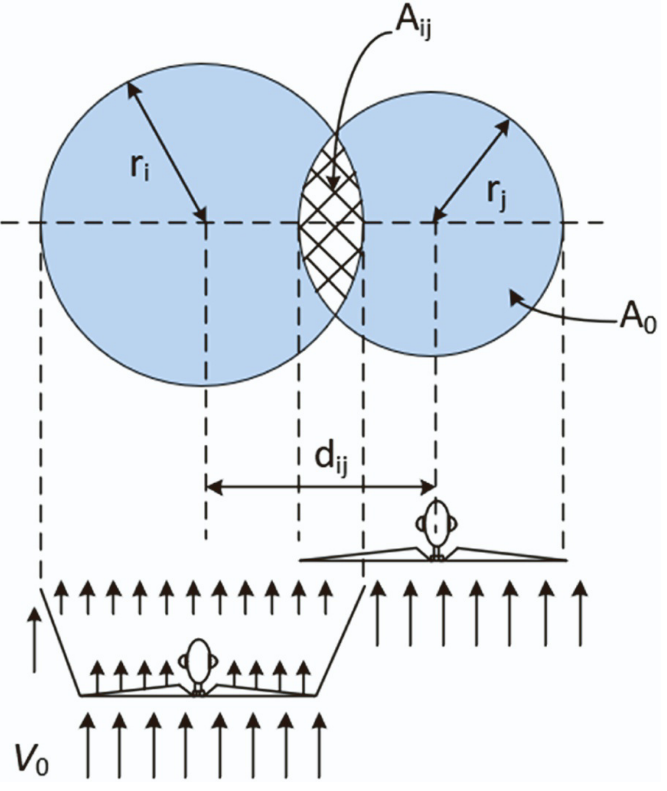
在实际风电场布局中，可以通过合理分组和布置涡轮位置，最大程度地降低尾流效应。在确定涡轮布局时，必须充分考虑上游涡轮尾流重叠对下游涡轮的影响。为提高尾流效应预测的准确性，需要计算阴影区域$A_{ij}$：
$$\begin{array}{rl}{A}_{ij}=& r_i^2{\cos }^{-1}\left(\frac{d_{ij}^2+r_i^2-r_j^2}{2d_{ij}{r}_i}\right)+r_j^2{\cos }^{-1}\left(\frac{d_{ij}^2+r_j^2-r_i^2}{2d_{ij}{r}_j}\right)\\ & -\frac{1}{2}\sqrt{\left(-d_{ij}+r_i+r_j\right)\left(d_{ij}-r_i+r_j\right)\left(-d_{ij}+r_i-r_j\right)\left(d_{ij}+r_i+r_j\right)}\end{array}$$

目标函数

风电场布局优化（WFLOP）需要综合考虑成本、发电量、环境影响和安全等多方面因素。当前常用的三种方法包括：

• 网格法：将风电场区域划分为多个网格，评估每个网格的风能资源，利用优化算法确定风机的数量和最优布局；

• 统计法：通过收集气象参数（如风速、风向等），采用统计建模的方法评估风能资源，实现风机布局优化；

• 多目标优化法：在最大化发电量和最小化成本等多重目标之间权衡，利用多种优化算法给出帕累托最优解。

本文采用网格法结合最大功率与最低成本两项指标：
$$Objective=\min \frac{Cost(N_{WT})}{P_{total}}$$

其中，$Cost(N_{WT})$表示风机总成本，$P_{tota}$表示总功率。风电场效率通过有尾流影响下总发电量与无尾流影响下总发电量比值计算：
$$Cost=N_{WT}\left(\frac{2}{3}+\frac{1}{3}{e}^{-0.00174N_{WT}^2}\right)$$
$$P_{total}=\sum _{i=1}^{N_{WT}}\frac{1}{2}{\eta }_i{\rho }_{air}{A}_i{V}_i^3$$
$${\eta }_{wf}=\frac{P_{total}}{N_{WT}\ast 0.3\ast {V_0}^3}$$

编码

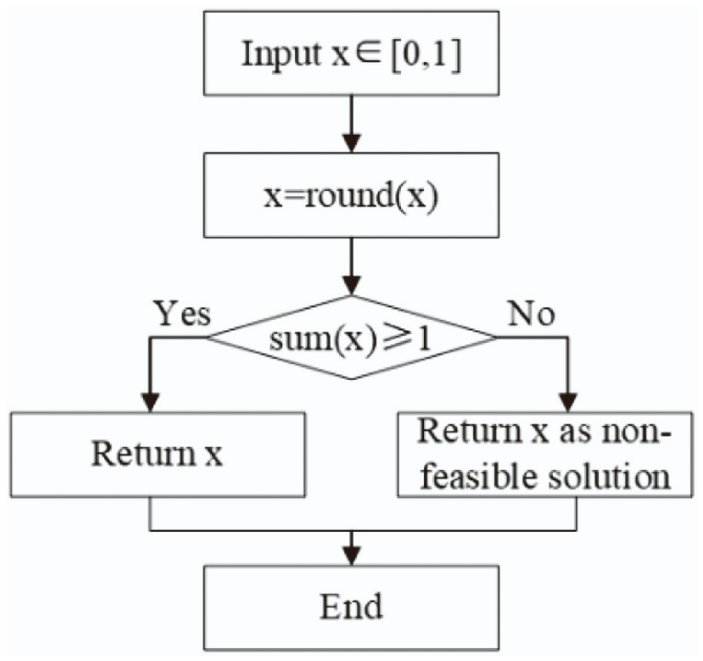
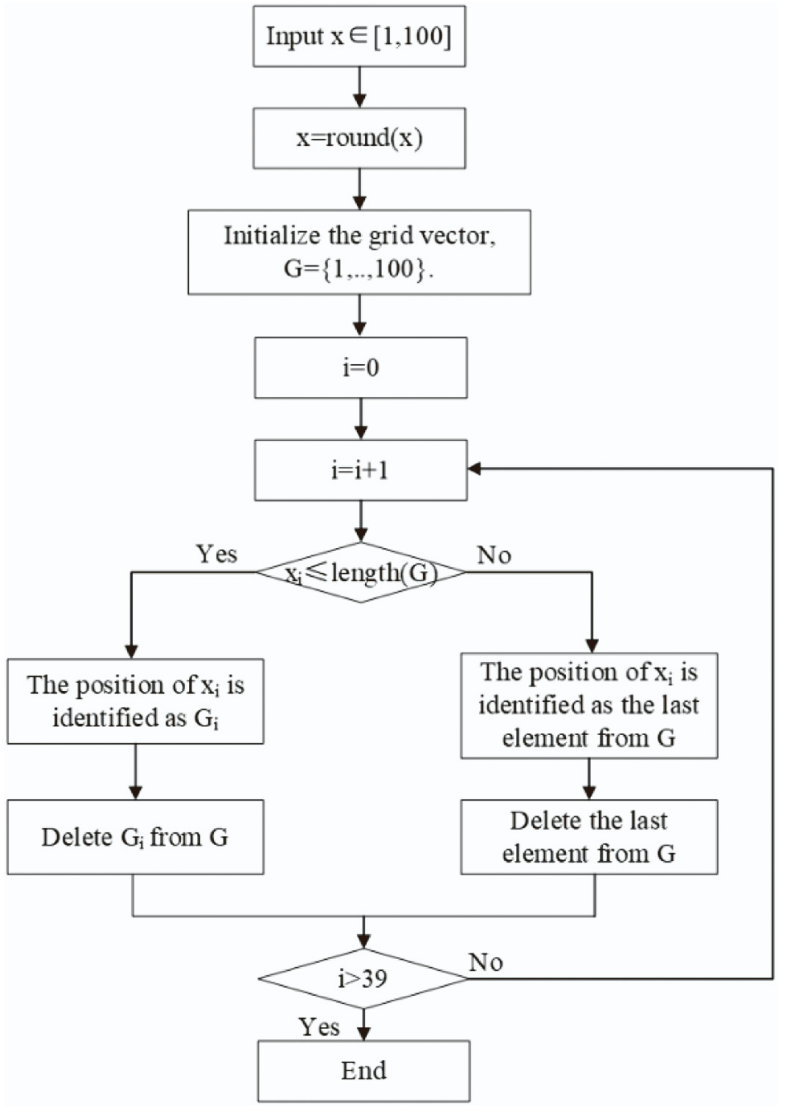
本文采用连续实数作为设计变量，来确定涡轮机在方格中的布置位置。

3.教与学优化算法TLBO原理

【智能算法】教与学优化算法 （TLBO）原理及实现

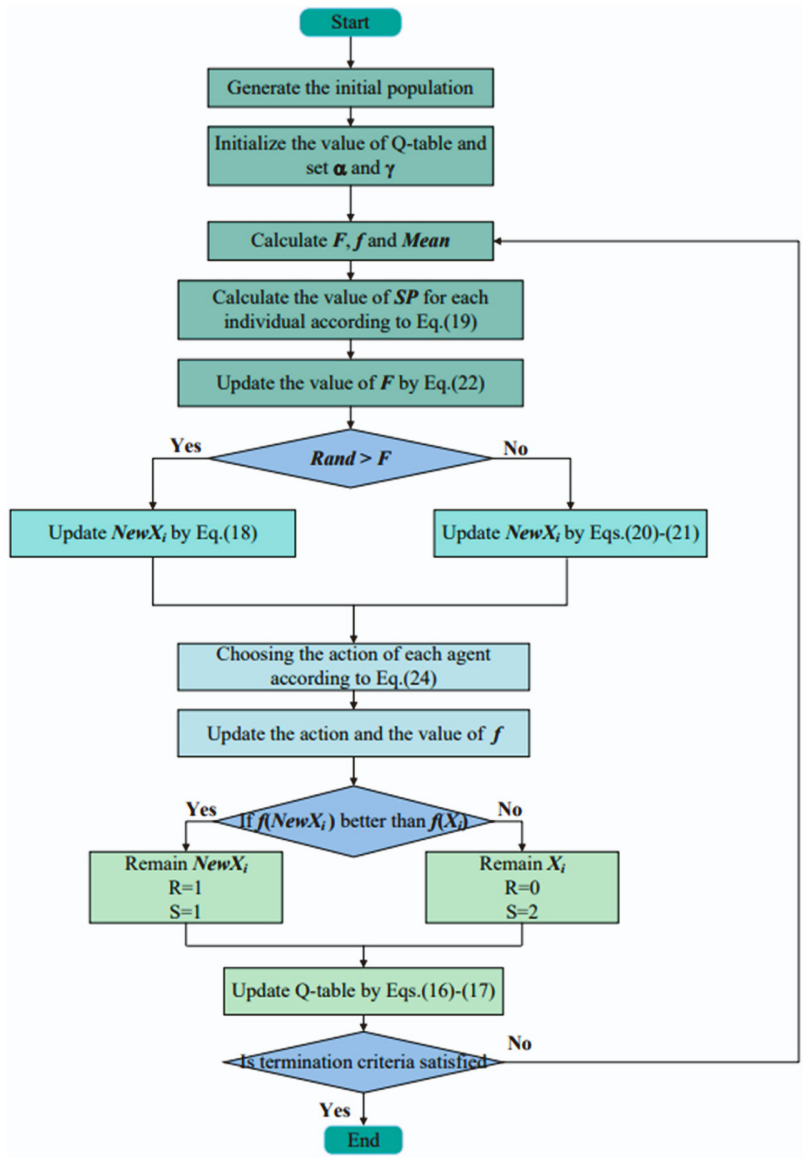
4.基于强化学习教与学优化算法RLPS-TLBO

RLPS-TLBO采用强化学习方法，根据每一代进化的结果，为每个个体自适应地调整参数$F$实现策略优化。当子代优于父代时，说明当前搜索方向有效，应增强局部搜索，即提高个体进入教师阶段的概率，此时设$f=-0.05$。若父代优于子代，说明当前搜索方向效果不佳，应增强全局搜索，提高个体选择学习者阶段的概率，此时$f=0.05$。对于其他情况，$f=0$。

每个智能体选择状态和动作的概率:
$$\pi \left(s_i,a_j\right)=\frac{e^{Q_t\left(s_i,a_j\right)/T}}{{\sum }_{j=1}^n{e}^{Q_t\left(s_i,a_j\right)/T}}$$

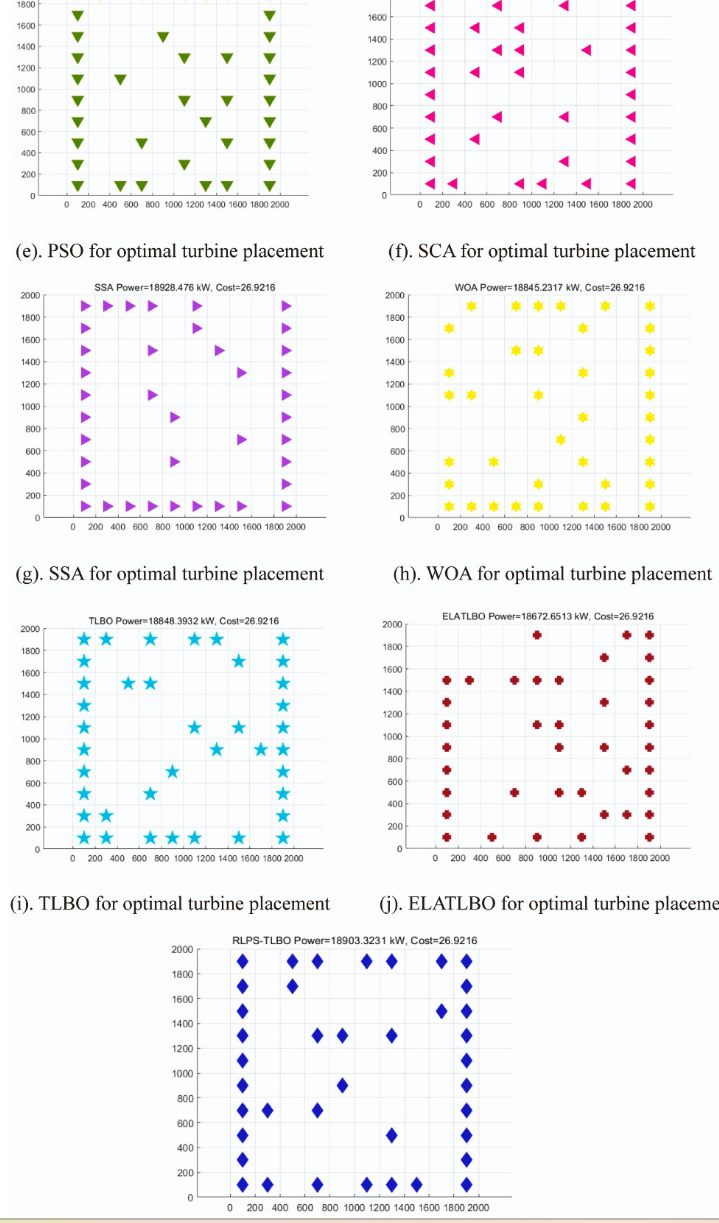
5.结果展示

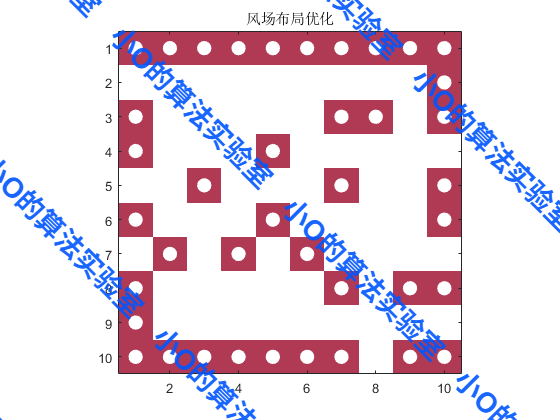
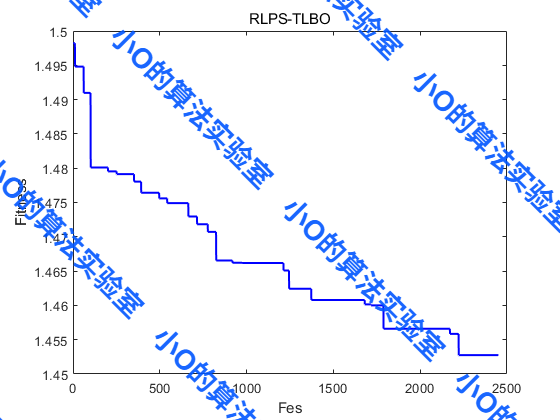
6.参考文献

[1] Yu X, Zhang W. A teaching-learning-based optimization algorithm with reinforcement learning to address wind farm layout optimization problem[J]. Applied Soft Computing, 2024, 151: 111135.

7.代码获取

xx

8.算法辅导·应用定制·读者交流