奇异值分解（Singular Value Decomposition, SVD）
奇异值分解（SVD） 是线性代数中一个极其重要的矩阵分解方法，适用于任意 的复数或实数矩阵。它不仅在理论分析中非常有用，还在机器学习、信号处理、统计学、图像压缩等领域有广泛的应用。
1. SVD 的定义
对于任意矩阵 ，其 SVD 分解为：
其中：
是左奇异向量矩阵（列向量是 的特征向量），且
是酉矩阵（
）。
是奇异值矩阵，其对角线元素 （
），其余位置为 0。
是右奇异向量矩阵（列向量是 的特征向量），且
是酉矩阵（
）。
2. SVD 的计算方法
（1）计算
和 
是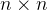 
的 Hermitian 矩阵，其特征值 
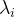是非负实数，且 
。
是
的 Hermitian 矩阵，其特征值与
的非零特征值相同。
（2）求 的特征值和特征向量
计算 的特征值
。 对应的单位特征向量
构成
的列。
（3）求 的特征向量
计算 的单位特征向量
，构成
的列。
对于非零奇异值 ，有：
（4）构造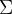 
是一个对角矩阵，其前 r 个对角元素是
，其余为 0。
3. SVD 的性质
奇异值的唯一性
奇异值 是唯一的。
但 和
的列向量（奇异向量）不唯一（可以乘以
仍满足分解）。
矩阵的秩
低秩近似（Eckart-Young 定理）
用前 k 个奇异值近似 ：
其中 只保留前 k 列，
只保留前 k 个奇异值。
这是最优低秩近似，即：
与特征分解的关系
（左奇异向量是
的特征向量）。
（右奇异向量是
的特征向量）。
4. 谱还原累加的步骤
还是按照上述理论，
计算 SVD：
选择前 k 个奇异值：
保留 ，其余设为 0。
重建矩阵：
其中 是仅保留前 k 个奇异值的对角矩阵。
等价的外积形式：
即逐层叠加 成分。
5. 谱还原累加的性质
最优低秩近似（Eckart-Young 定理）：
其中 是 Frobenius 范数。
能量占比：
前 k 个奇异值的能量占比：
可用于决定保留多少奇异值（如 PCA 中选取主成分）。
压缩与去噪：
图像压缩：仅存储 ,
,
可大幅减少数据量。
信号去噪：丢弃较小的奇异值（通常对应噪声）。
6. SVD 的应用
（1）矩阵求逆与伪逆（Moore-Penrose 伪逆）
如果 ，则其伪逆：
其中 是
的伪逆（非零元素取倒数再转置）。
（2）主成分分析（PCA）
PCA 本质上是数据协方差矩阵 的 SVD 分解。
（3）图像压缩
保留前 k个奇异值，可以大幅减少存储空间：
（4）推荐系统（协同过滤）
SVD 用于降维，提取用户和物品的潜在特征。
（5）最小二乘问题
求解 时，SVD 提供稳定解。
7. 小矩阵计算示例
设矩阵：
计算 SVD：
计算 和
：
求 的特征值
，对应奇异值
。
计算 和
：
的列是
的特征向量。
的前两列由
计算，最后一列由 Gram-Schmidt 正交化得到。
最终 SVD：
8. 小结
SVD 适用于任意矩阵，而特征分解仅适用于方阵。
奇异值 是非负的，并按降序排列。
SVD 可用于矩阵近似、降维、求伪逆、PCA、图像压缩等。
计算 SVD 通常使用数值方法（如 QR 迭代；使用数值软件：LAPACK，openblas，cusolver），而非手动计算（除非矩阵很小）。
SVD 是数据科学和工程中的核心工具